محاسبه خطای آزمایش اصطکاک – از صفر تا صد


در این مطلب در مورد خطای آزمایش اصطکاک صحبت میکنیم. اصطکاک نیرویی است که در برابر حرکت مقاومت میکند و البته به حرکت ما نیز کمک میکند. در این مطلب ابتدا انواع نیرو را معرفی میکنیم و سپس به صورت خاص انواع نیروی اصطکاک و ویژگیهای آن را بررسی و معرفی خواهیم کرد. همچنین روشهای مختلف آزمایش اصطکاک را معرفی کرده و در نهایت خطای آزمایش اصطکاک را محاسبه خواهیم کرد.
نیرو چیست؟
نیرو فشار یا کششی است که بر یک جسم در نتیجه تعامل آن با جسم دیگر وارد میشود.
انواع مختلفی از نیروها وجود دارد که این نیروها بر اساس اینکه نیرو ناشی از تماس یا عدم تماس دو جسم متقابل است، در دو دسته کلی تقسیم میشوند.

| نیروهای تماسی | نیروهای غیرتماسی |
| نیروی اصطکاک | نیروی گرانشی |
| نیروی کششی | نیروی الکتریکی |
| نیروی عمود بر سطح یا نیروی نرمال | نیروی مغناطیسی |
| نیروی مقاومت هوا | |
| نیروی محرک یا ورودی | |
| نیروی فنر |
انواع نیروها و علامت اختصاری آنها را در ادامه به اختصار توضیح میدهیم.
نیروی محرک یا ورودی
نیروی ورودی یا محرک، نیرویی است که توسط شخص یا جسم دیگری به جسم وارد میشود. اگر شخصی در حال هل دادن میز در سراسر یک اتاق باشد، نیرویی بر جسم وارد میشود. نیروی محرک به صورت عمومی به عنوان نیرویی شناخته میشود که یک فرد به یک جسم اعمال میکند.
نیروی گرانش یا وزن
نیروی گرانش نیرویی است که با آن زمین، ماه، یا سایر اجسام بسیار بزرگ جسم دیگری را به سمت خود جذب میکنند. طبق تعریف، این کمیت برابر با وزن جسم است. تمام اجسام روی زمین نیروی گرانشی را تجربه میکنند که آنها را به سمت مرکز زمین و به سمت پایین میکشد. نیروی گرانش روی زمین همیشه برابر با وزن جسم است که با معادله زیر بدست میآید:
که نیوتن بر کیلوگرم (روی زمین) و m = جرم (بر حسب کیلوگرم) است.
نیروی عمود بر سطح
نیروی نرمال یا عمود بر سطح، نیروی پشتیبانی است که بر جسمی وارد میشود که با جسم ثابت دیگری در تماس است. به عنوان مثال، اگر کتابی بر روی سطحی قرار گرفته باشد، سطح آن به منظور تحمل وزن کتاب، نیرویی رو به بالا بر کتاب وارد میکند. در مواردی، یک نیروی عمود بر سطح به صورت افقی بین دو جسمی که با یکدیگر در تماس هستند وارد می شود. به عنوان مثال، اگر فردی به دیوار تکیه دهد، دیوار به صورت افقی به فرد فشار می آورد.
نیروی اصطکاک
نیروی اصطکاک نیرویی است که توسط یک سطح به هنگام حرکت جسم بر روی آن یا جسمی که در تلاش است تا بر روی جسم دیگر حرکت کند وارد میشود. حداقل دو نوع نیروی اصطکاک وجود دارد که عبارت از اصطکاک جنبشی و استاتیک هستند. اگرچه همیشه اینطور نیست، اما عموماً نیروی اصطکاک اغلب با حرکت یک جسم مخالف است. برای مثال، اگر کتابی روی سطح میز بلغزد، میز در خلاف جهت حرکت خود نیروی اصطکاک وارد میکند. اصطکاک ناشی از فشرده شدن دو سطح به یکدیگر است که باعث ایجاد نیروهای جاذبه بین مولکولهای سطوح مختلف میشود. به این ترتیب، اصطکاک به ماهیت دو سطح و میزان فشرده شدن آنها به یکدیگر نیز بستگی دارد. حداکثر نیروی اصطکاک که یک سطح میتواند بر یک جسم وارد کند را میتوان با استفاده از فرمول زیر محاسبه کرد:
نیروی مقاومت هوا
نیروی مقاومت هوا نوع خاصی از نیروی اصطکاک است که بر روی اجسام هنگام حرکت در هوا تأثیر میگذارد. نیروی مقاومت هوا اغلب برای مخالفت با حرکت یک جسم مشاهده میشود. این نیرو به دلیل اندازه ناچیز آن (و به دلیل اینکه پیش بینی مقدار آن از نظر ریاضی دشوار است) اغلب نادیده گرفته میشود. این نیرو برای اجسامی که با سرعت بالا حرکت میکنند (مانند چترباز یا اسکی باز) یا برای اجسامی با سطح بزرگ بیشتر قابل توجه است.
نیروی کششی
نیروی کششی نیرویی است که از طریق یک ریسمان، طناب، کابل یا سیم، هنگامی که یک جسم توسط نیروهایی که از دو طرف مخالف وارد میشوند، منتقل میشود. نیروی کشش در طول سیم امتداد مییابد و به طور مساوی بر روی اجسام در انتهای مخالف سیم اثر میگذارد.
نیروی فنر
نیروی فنر نیرویی است که توسط یک فنر فشرده شده یا کشیده شده به هر جسمی که به آن متصل است وارد میشود. جسمی که فنر را فشرده یا کشیده میکند همیشه با نیرویی فنر که میخواهد آن را به حالت تعادل بازگرداند، مخالفت میکند. برای اکثر فنرها، مخصوصاً آنهایی که از قانون هوک پیروی میکنند، بزرگی نیرو با مقدار کشش یا فشرده سازی فنر نسبت مستقیم دارد.
نیروی اصطکاک چیست؟
اصطکاک نیرویی است که همیشه در اطراف ما است و با حرکت نسبی بین سیستمهایی که در تماس با یکدیگر هستند مخالفت میکند اما به ما اجازه حرکت میدهد. این موضوع را اگر تا به حال سعی کردهاید روی یخ راه بروید، کشف کردهاید. اصطکاک در حالی که یک نیروی معمول است اما در واقع دارای رفتاری بسیار پیچیده است و هنوز به طور کامل درک نشده است. برای درک بیشتر آن میتوانیم به مشاهدات تکیه کنیم.
با این حال، هنوز هم ویژگیهای اولیهای در این نیرو وجود دارد که میتوانیم با مشاهده، آنها را درک کنیم. یکی از ویژگیهای ساده اصطکاک این است که موازی با سطح تماس بین سیستمها و همیشه در جهتی است که با حرکت یا تلاش سیستمها نسبت به یکدیگر مخالف است. اگر دو سیستم در تماس و حرکت نسبت به یکدیگر باشند، اصطکاک بین آنها اصطکاک جنبشی نامیده میشود. به عنوان مثال، اصطکاک حرکت هاکی را که روی یخ میلغزد، کند میکند. اما هنگامی که اجسام ساکن هستند، اصطکاک ساکن یا ایستائی بین آنها عمل میکند. معمولاً اصطکاک استاتیک یا ایستائی بیشتر از اصطکاک جنبشی بین اجسام است.
برای مثال تصور کنید که سعی میکنید یک جعبه سنگین را روی کف بتنی بکشید، ممکن است شما هر چه بیشتر و بیشتر به جعبه فشار بیاورید ولی نتوانید آن را به هیچ وجه حرکت دهید. این بدان معنی است که اصطکاک استاتیک به آنچه شما انجام میدهید، پاسخ میدهد و افزایش مییابد و برابر و در جهت مخالف فشار شما اعمال میشود. اما اگر در نهایت به اندازه کافی فشار وارد کنید، به نظر میرسد که جعبه ناگهان میلغزد و شروع به حرکت میکند. هنگامی که در حرکت هستید، راحتتر میتوانید آن را در حالت سکون اولیه نگه دارید و این نشان میدهد که نیروی اصطکاک جنبشی کمتر از نیروی اصطکاک استاتیک است. اگر به جعبه جرم اضافه کنید، مثلاً با قرار دادن یک جعبه در بالای آن، باید برای شروع به حرکت آن و همچنین برای حرکت دادن مجدد آن با نیروی بیشتری فشار وارد کنید. علاوه بر این اگر سطح بتن را روغن کاری کرده باشید، شروع به حرکت و ادامه حرکت جعبه همان طور که انتظار دارید، آسانتر خواهد بود.
تصویر (1) نمایشی از نحوه ایجاد اصطکاک در سطح بین دو جسم است. نگاه کردن از نزدیک به این سطوح زبر بودن آنها را نشان میدهد. بنابراین وقتی برای حرکت دادن یک جسم (در این مورد یک جعبه) نیرو وارد میکنید، باید شی را بالا بیاورید تا زمانی که بتواند همراه با نوک سطح برخورد کند یا این نقاط برجسته را بشکند یا هر دو حالت با هم اتفاق بیفتد. با اصطکاک و بدون حرکت ظاهری میتوان در برابر نیروی قابل توجهی مقاومت کرد. هرچه سطوح به یکدیگر محکمتر فشار داده شوند، مانند اینکه جعبه دیگری روی جعبه قرار گیرد، نیروی بیشتری برای جابجایی آنها لازم است. بخشی از اصطکاک ناشی از نیروهای چسبنده بین مولکولهای سطحی دو جسم است که وابستگی اصطکاک به ماهیت مواد را توضیح میدهد.
چسبندگی با مواد در تماس متفاوت است و جنبه پیچیدهای از فیزیک سطح است. هنگامی که یک جسم در حال حرکت است، نقاط تماس کمتری یعنی چسبندگی مولکولهای کمتری وجود دارد و بنابراین نیروی کمتری برای حرکت جسم مورد نیاز است. در سرعتهای کوچک اما غیر صفر، اصطکاک تقریباً مستقل از سرعت است.

نیروهای اصطکاکی، مانند f همیشه با حرکت یا تلاش برای حرکت بین اجسام در تماس با یکدیگر مخالفت میکند. اصطکاک تا حدی به دلیل ناهمواری سطوح در تماس یکدیگر است، همانطور که در تصویر (1) نیز دیده میشود. برای اینکه جسمی حرکت کند، باید بلند شود و به جایی برسد که قلهها بتوانند در امتداد سطح پایینی بپرند. بنابراین نیرو فقط برای به حرکت درآوردن جسم مورد نیاز است. در این حالت برخی از قلهها شکسته میشوند و جسم به حرکت در میآید. با این حال به نیرویی برای حفظ حرکت نیز نیاز است. بیشتر اصطکاک در واقع به دلیل نیروهای جاذبه بین مولکولهای سازنده دو جسمی است که روی هم قرار گرفتهاند، به طوری که حتی سطوح کاملاً صاف نیز عاری از اصطکاک نیستند. چنین نیروهای چسبندهای به موادی که سطوح از آن ساخته شدهاند نیز بستگی دارد. این ویژگی برای مثال توضیح میدهد که چرا کفشهای با کف لاستیکی کمتر از کفشهای دارای کف چرمی میلغزند.
مقدار نیروی اصطکاک دو شکل دارد: یکی برای موقعیتهای ایستا (اصطکاک استاتیک)، دیگری برای زمانی که حرکت وجود دارد (اصطکاک جنبشی). هنگامی که هیچ حرکتی بین اجسام وجود ندارد اصطکاک، ایستائی یا استاتیک است و آن را با نمایش میدهند و رابطه آن به صورت نوشته میشود، که در آن ضریب اصطکاک ایستایی و N مقدار نیروی نرمال یا نیروی عمود بر سطح است. در این رابطه ضریب اصطکاک ایستائی و نیروی عمود بر سطح است.
علامت به معنی کمتر یا مساوی، به این معنی است که اصطکاک ایستائی میتواند کمتر یا حداکثر مقدار را داشته باشد. اصطکاک ایستائی یک نیروی عکس العمل است که تا حداکثر حد خود افزایش مییابد تا برابر و مخالف هر نیرویی باشد که اعمال میشود. هنگامی که نیروی اعمال شده از بزرگتر شود، جسم شروع به حرکت میکند. بنابراین حالت بیشینه اصطکاک ایستائی زمانی است که باشد.
هنگامی که یک جسم در حال حرکت است، مقدار اصطکاک جنبشی یا با داده میشود، که در آن ضریب اصطکاک جنبشی است. سیستمی که در آن است به عنوان سیستمی توصیف میشود که در آن اصطکاک به سادگی رفتار میکند. در رابطه اصطکاک جنبشی ضریب اصطکاک جنبشی و نیروی عمود بر سطح است.
همان طور که در جدول 1 مشاهده میشود، ضرایب اصطکاک جنبشی یک جسم کمتر از ضرایب اصطکاک استاتیک یا ایستائی هستند. این که مقادیر در جدول 1 تنها با یک یا حداکثر دو رقم اعشار بیان شده است، نشان دهنده توصیف تقریبی اصطکاک است که توسط دو معادله فوق ارائه شدهاند.
| سیستم | ضریب اصطکاک ایستائی | ضریب اصطکاک جنبشی |
| لاستیک روی بتن خشک | ||
| لاستیک روی بتن مرطوب | ||
| چوب روی چوب | ||
| چوب صاف شده روی برف خیس | ||
| فلز روی چوب | ||
| فولاد روی فولاد خشک | ||
| فولاد روی فولاد روغن کاری شده | ||
| تفلون روی فولاد | ||
| استخوان روغن کاری شده توسط مایع سینوویال | ||
| کفش روی چوب | ||
| کفش روی یخ | ||
| یخ روی یخ | ||
| فولاد روی یخ |
معادلاتی که در مورد اصطکاک داده شد شامل وابستگی اصطکاک به جنس مواد و نیروی نرمال یا عمود بر سطح است. جهت اصطکاک همیشه خلاف جهت حرکت، موازی با سطح بین اجسام و عمود بر نیروی نرمال است. به عنوان مثال، اگر جعبهای که میخواهید با نیرویی موازی با کف حرکت دهید، دارای جرم 100 کیلوگرم باشد، نیروی نرمال برابر با وزن آن خواهد بود و داریم:
جهت این نیرو عمود بر سطح است. اگر ضریب اصطکاک استاتیکی باشد، برای حرکت جعبه باید نیرویی موازی با کف و بیشتر از اعمال کنید. هنگامی که حرکت وجود دارد، اصطکاک کمتر است و ضریب اصطکاک جنبشی ممکن است باشد، به طوری که نیرویی تنها با بزرگی میتواند حرکت را با سرعت ثابت نگه دارد. اگر کف روغن کاری شود، هر دو ضریب به طور قابل توجهی کمتر از ضریب بدون روغن کاری هستند. ضریب اصطکاک یک ضریب کمتر از یک و با مقداری معمولاً بین 0 تا ۱ است. این ضریب به دو سطحی که در تماس با یکدیگر هستند بستگی دارد.
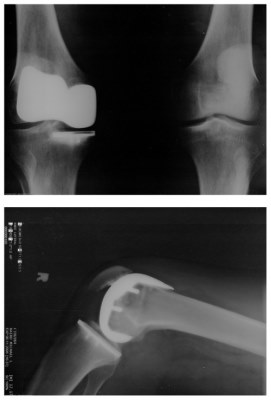
بسیاری از افراد لغزندگی راه رفتن روی یخ را تجربه کردهاند. با این حال، بسیاری از قسمتهای بدن، به ویژه مفاصل، دارای ضریب اصطکاک بسیار کمتری اغلب سه یا چهار برابر کمتر از یخ هستند. یک مفصل از انتهای دو استخوان تشکیل میشود که توسط بافتهای ضخیم به هم متصل شدهاند. مفصل زانو از استخوان ساق پا (درشت نی) و استخوان ران (فمور) تشکیل میشود. مفصل ران یک توپ (در انتهای استخوان ران) و حفره (بخشی از لگن) است. انتهای استخوانهای مفصل توسط غضروف پوشانده شده است که سطحی صاف و تقریباً شیشهای ایجاد میکند. مفاصل همچنین یک مایع (مایع سینوویال) تولید میکنند که اصطکاک و سایش را کاهش میدهد. مفصل آسیب دیده یا آرتروز را میتوان با یک مفصل مصنوعی جایگزین کرد که این موضوع در تصویر (۲) نمایش داده شدهاند. این جایگزینها میتوانند از فلزات (فولاد ضد زنگ یا تیتانیوم) یا پلاستیک (پلی اتیلن)، با ضریب اصطکاک بسیار کمی ساخته شوند.
مثال: یک اسکی باز با وزن 62 کیلوگرم در حال سر خوردن از یک شیب برفی است. اگر نیروی اصطکاک 45 نیوتن باشد، ضریب اصطکاک جنبشی را برای اسکی باز بیابید.
پاسخ: مقدار اصطکاک جنبشی 45 نیوتن است. بنابراین، ضریب اصطکاک جنبشی را اگر بتوانیم نیروی نرمال اسکی باز را در یک شیب پیدا کنیم، قابل محاسبه است. نیروی نرمال همیشه عمود بر سطح است و از آنجایی که هیچ حرکتی عمود بر سطح وجود ندارد، نیروی نرمال باید با مولفه وزن اسکی باز عمود بر شیب برابر باشد. (نیروهای وارد بر اسکی باز را در تصویر پایین ببینید.)
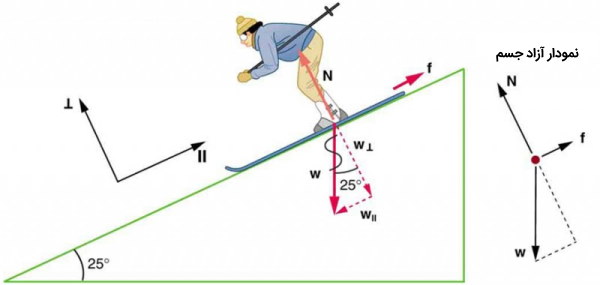
حرکت اسکی باز و اصطکاک در راستای شیب است و بنابراین بسیار راحت است که همه نیروها را بر روی یک سیستم مختصات قرار دهیم که در آن یک محور موازی با شیب و دیگری عمود بر آن باشد. این محورها در سمت چپ اسکی باز نشان داده شدهاند. N (نیروی نرمال) عمود بر شیب است و f (اصطکاک) موازی با شیب است، اما W (وزن اسکی باز) دارای مولفههایی در امتداد هر دو محور یعنی و است. مقدار N برابر با است، بنابراین هیچ حرکتی عمود بر شیب وجود ندارد. با این حال f از نظر مقدار کمتر از است، بنابراین شتابی به سمت پایین سطح شیبدار و در راستای وجود دارد. در حقیقت داریم:
با جایگزینی این عبارت برای اصطکاک جنبشی داریم:
که اکنون میتوان ضریب اصطکاک جنبشی یعنی را به دست آورد.
مقداری که از این روش به دست میآید کمی کوچکتر از ضریب ذکر شده در جدول ضرایب اصطکاک برای چوب روی برف است، اما مقدار آن همچنان معقول است زیرا مقادیر ضرایب اصطکاک میتوانند بسیار متفاوت باشند. در موقعیتهایی مانند این، جایی که جسمی به جرم m از شیبی به پایین میلغزد که زاویه را با سطح افقی ایجاد میکند، اصطکاک با به دست میآید. در این شرایط همه اجسام با شتاب ثابت از شیب به پایین میلغزند.
اگر نیروی خالص وارد بر جسم صفر باشد، یک جسم با سرعت ثابت از صفحه شیبدار به پایین میلغزد. میتوانیم از این واقعیت برای اندازه گیری ضریب اصطکاک جنبشی بین دو جسم استفاده کنیم. همانطور که در پرسش بالا نشان داده شده است، نیروی اصطکاک جنبشی در یک سطح شیبدار برابر با است. مولفه وزن به سمت پایین شیب برابر است که نمودار نیروها را میتوانید در شکل بالا ببینید. این نیروها در جهت مخالف عمل میکنند، بنابراین وقتی اندازه آنها مساوی باشند، شتاب حرکت صفر است. بدین ترتیب داریم:
برای به دست آوردن داریم:
یک سکه را روی یک کتاب بگذارید و آن را کج کنید تا سکه با سرعت ثابتی روی کتاب بلغزد. ممکن است لازم باشد به آرامی روی کتاب ضربه بزنید تا سکه حرکت کند. زاویه انحراف را نسبت به راستای افقی اندازه بگیرید و را محاسبه کنید. توجه داشته باشید که سکه به هیچ وجه شروع به لغزش نمیکند تا زمانی که زاویهای بزرگتر از به دست آید، زیرا ضریب اصطکاک ساکن بزرگتر از ضریب اصطکاک جنبشی است.
بدین ترتیب نشان دادیم که وقتی جسمی بر روی یک سطح افقی قرار میگیرد، نیروی عمود بر سطح آن را تحمل میکند که مقدار آن برابر با وزنش است. علاوه بر این، نیروی اصطکاک معمولی همیشه با نیروی نرمال متناسب است.
جنبههای سادهتر اصطکاک که تاکنون به آن پرداخته شده، ویژگیهای ماکروسکوپی (در مقیاس بزرگ) آن است. در چند دهه گذشته گامهای بزرگی در توضیح مقیاس اتمی اصطکاک نیز برداشته شده است. محققان دریافتهاند که به نظر میرسد ماهیت اتمی اصطکاک دارای چندین ویژگی اساسی است. این ویژگیها نه تنها برخی از جنبههای سادهتر اصطکاک را توضیح میدهند، بلکه پتانسیل ایجاد محیطهای تقریباً بدون اصطکاک را نیز دارند که میتواند صدها میلیارد دلار در انرژی که در حال حاضر به گرما تبدیل میشود، صرفهجویی کند.
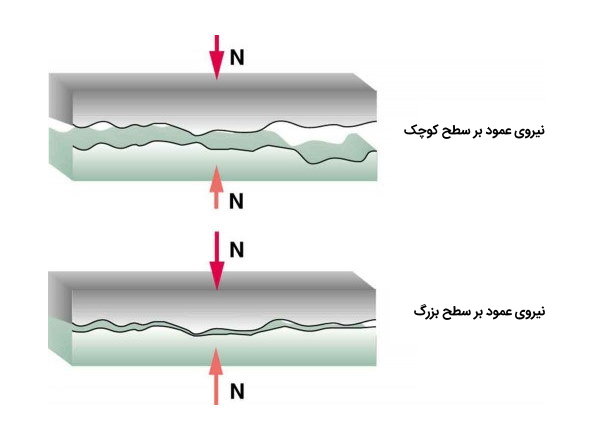
تصویر (۳) یک ویژگی ماکروسکوپی اصطکاک را نشان میدهد که توسط تحقیقات میکروسکوپی (در مقیاس کوچک) توضیح داده شده است. در مثالهای بالا نشان دادیم که اصطکاک با نیروی عمود بر سطح یا نرمال متناسب است، اما ارتباطی با ناحیهای که با آن در تماس است، ندارد. این تصور تا حدی خلاف واقع است. هنگامی که دو سطح ناهموار در تماس با یکدیگر هستند، منطقه تماس واقعی کسری کوچک از کل مساحت است زیرا فقط نقاط مرتفع لمس میشوند. هنگامی که نیروی نرمال بیشتری اعمال میشود، سطح تماس واقعی افزایش مییابد و مشخص است که مقدار اصطکاک با ناحیه تماس متناسب است.
تصویر (۳) دارای دو قسمت است که هر کدام دو سطح ناهموار را در مجاورت یکدیگر نشان میدهند. در قسمت اول، نیروی نرمال کم است، به طوری که سطح تماس بین دو سطح بسیار کوچکتر از مساحت کل آنها است. در قسمت دوم، نیروی نرمال زیاد است، به طوری که سطح تماس بین دو سطح افزایش یافته است. در نتیجه اصطکاک بین دو سطح در قسمت دوم نیز بیشتر از اصطکاک قسمت اول است.
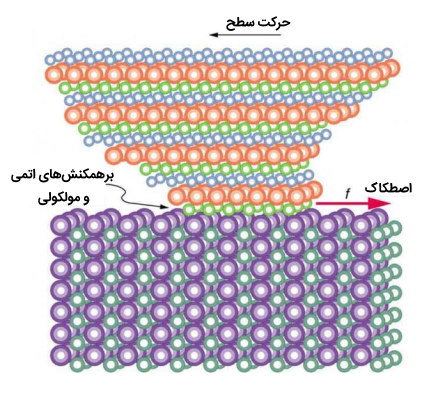
دیدگاه در مقیاس اتمی نوید این را میدهد که ویژگیهای سادهتر اصطکاک را بیشتر توضیح دهند. مکانیسم چگونگی تولید گرما اکنون در حال بررسی بیشتر است. به عبارت دیگر، سوال اساسی این است که چرا سطوح هنگام مالش گرمتر میشوند؟ اساساً اتم ها به یکدیگر متصل میشوند تا شبکههایی را تشکیل دهند. وقتی سطوح ساییده میشوند، اتمهای سطحی به هم میچسبند و باعث میشوند شبکههای اتمی ارتعاش کنند و اساساً امواج صوتی ایجاد میکنند که به مواد نفوذ میکنند. امواج صوتی با افزایش فاصله کاهش مییابند و انرژی آنها به گرما تبدیل میشود. واکنشهای شیمیایی که مربوط به سایش اصطکاکی است نیز میتوانند بین اتمها و مولکولهای روی سطوح رخ دهد. تصویر (۴) نشان میدهد که چگونه نوک یک جسم کشیده شده روی یک ماده دیگر توسط اصطکاک در مقیاس اتمی تغییر شکل میدهد. نیروی مورد نیاز برای کشیدن نوک را میتوان اندازه گیری کرد و مشخص میشود که این نیرو مربوط به تنش برشی است. تغییرات تنش برشی قابل توجه است و مقداری در اندازهای بیش از دارد و پیشبینی تئوری آن دشوار است، با این حال تنش برشی درکی اساسی از پدیدهای در مقیاس بزرگ که از دوران باستان شناخته شده است یعنی اصطکاک ارائه میدهد.
آزمایش محاسبه ضریب اصطکاک
برای محاسبه ضریب اصطکاک ایستائی و جنبشی در آزمایشگاه روشهای مختلفی وجود دارد. همچنین این ضرایب را میتوان در حالتهای سطح افقی و سطح شیبدار و برای جنس مختلف سطوح نیز به دست آورد. در ادامه این روشها و روش محاسبه خطای اصطکاک را توضیح میدهیم.
محاسبه ضریب اصطکاک و محاسبه خطای اصطکاک در یک سطح افقی
تصویر زیر را برای یک سطح افقی در نظر بگیرید:
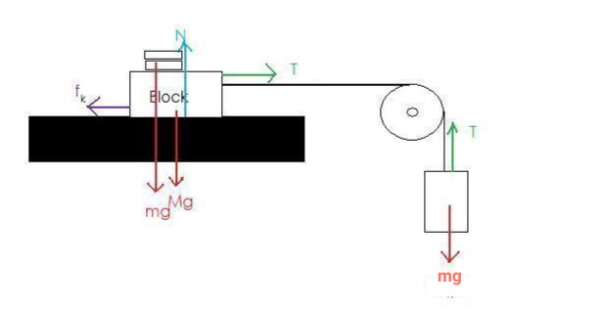
در ابتدا میخواهیم ضریب اصطکاک ایستائی را به دست آوریم. بدین منظور به ریسمان آویزان از قرقره جرم اضافه میکنیم تا زمانی که جسم روی سطح در آستانه حرکت قرار بگیرد. منظور از آستانه حرکت، زمانی است که با تقه زدن روی سطح جسم کمی جابجا شود و سپس متوقف شود. در این حالت میتوان ضریب اصطکاک ایستائی را با توجه به روابط زیر به دست آورد:
رابطه بالا بر روی سطح برقرار است و رابطه برای سطحی که از قرقره آویزان است برقرار خواهد بود. دقت کنید که نیروی کشش ریسمان در کل طول طناب یکسان در نظر گرفته شده است و همچنین از اصطکاک قرقره صرف نظر کردهایم. بدین ترتیب داریم:
و ضریب اصطکاک ایستائی سطح برابر است با:
همین روش را برای ضریب اصطکاک جنبشی نیز تکرار میکنیم، با این تفاوت که در این مرحله با اضافه کردن وزنه و با زدن یک ضربه به سطح، جسم روی سطح افقی با سرعت ثابت شروع به حرکت کند. در این حالت از آزمایش به شرط حرکت با سرعت ثابت دقت کنید. بدین ترتیب داریم:
برای این که دقت آزمایش را بالا ببریم. این آزمایش را برای حالتها، یعنی وزنههای متفاوتی روی سطح تکرار میکنیم. ممکن است با توجه به توضیحات بالا این سوال پیش بیاید که وقتی از لحاظ میکروسکوپی به سطح نگاه میکنیم و جسم بیشتری روی سطح قرار دهیم، درگیری بین مولکولهای سطح و جسم بیشتر خواهد بود و ضریب اصطکاک باید مقدار بیشتری را نشان دهد. این فرض را نیز در این آزمایش در نظر میگیریم که اصطکاک را از لحاظ ماکروسکوپیک بررسی میکنیم.
برای مثال میتوان برای جرمهای روی سطح مقادیر ، ، و گرم را در نظر بگیریم. مقادیری که برای و که در این حالتها به دست آوردهایم با یکدیگر جمع میکنیم و بر تعداد انجام آزمایش که در این حالت 4 بار تکرار شده تقسیم میکنیم.
مقدار میانگین به دست آمده برابر با ضریب اصطکاک سطح است. برای محاسبه خطای آزمایش اصطکاک دو روش را میتوان پیشنهاد کرد. اگر در آزمایشگاه شما جدولی برای مقدار ضریب اصطکاک وجود دارد، برای محاسبه خطای آزمایش اصطکاک میتوان قدر مطلق تفاضل مقدار داده شده در جدول را از مقدار میانگین محاسبه کرد و این مقدار برابر با خطای مطلق است. همچنین برای به دست آوردن خطای نسبی نیز باید مقدار خطای مطلق را بر مقدار داده شده در جدول تقسیم کرد.
همان طور که میدانید خطای مطلق دارای واحد خود کمیت و خطای نسبی بدون واحد است. اما در این حالت چون کمیتی که اندازه گیری کردیم خطای آزمایش اصطکاک است و ضریب اصطکاک کمیتی بدون بعد است هر دو خطا یعنی مطلق و نسبی واحد ندارند.
اگر جدول دادهای در آزمایشگاه شما وجود ندارد، بدین معنی است که مقدار میانگینی که به دست آوردید برابر با مقدار حقیقی ضریب اصطکاک است. بدین ترتیب باید برای محاسبه خطای آزمایش اصطکاک مقدار میانگین را از هر یک از مقادیر به دست آمده در آزمایش کم کنید (تفاضل قدر مطلق)، تا خطای آزمایش اصطکاک و در حقیقت خطای مطلق آن را به دست آوردید. با تقسیم مقادیر خطای مطلق بر مقدار میانگین، خطای نسبی نیز به دست میآید.
محاسبه ضریب اصطکاک و محاسبه خطای اصطکاک در یک سطح شیبدار
آزمایش بالا را میتوان برای یک سطح شیبدار نیز تکرار کرد. در این حالت آزمایش را میتوان به ازای زوایای مختلف سطح شیبدار و اجسامی با جرمهای متفاوت روی سطح شیبدار انجام داد. روش کار برای به دست آوردن ضریب اصطکاک ایستائی و جنبشی مانند حالت قبل است. اما رابطه به دست آوردن ضرایب اصطکاک متفاوت است. در حقیقت برای یک جسم روی سطح شیبدار و در حالت آستانه حرکت به سمت بالای سطح شیبدار داریم:
از طرفی برای جسمی که از ریسمان آویزان است نیز داریم:
با جایگذاری رابطه دوم در رابطه اول، برای ضریب اصطکاک ایستائی داریم:
این رابطه برای ضریب اصطکاک جنبشی نیز با این شرط که حرکت با سرعت ثابت انجام میشود، برقرار است و داریم:
این آزمایش را همان طور که گفته شد میتوان برای مقادیر مختلف زاویه سطح شیبدار و جرمهای متفاوت آویزان از سطح انجام داد تا دقت اندازهگیری و خطای آزمایش اصطکاک را کاهش دهیم. مانند حالت قبل میتوانیم جوابهای به دست آمده را با مقادیر داده شده در جدول آزمایشگاه یا مقدار میانگین به دست آمده مقایسه کنیم و خطای آزمایش اصطکاک را به دست آوریم.
مثالی از انجام آزمایش محاسبه ضریب اصطکاک جنبشی
در این آزمایش برای محاسبه ضریب اصطکاک جنبشی مانند تصویر (۵)، از یک سطح چوبی کوچک استفاده کردیم که یک طرف آن با نوار تفلون پوشانده شده بود. یک بلوک را روی آن قرار دادیم که به آن یک ریسمان متصل است. ریسمان از طریق یک قرقره به جسم دیگری که از آن آویزان است، متصل شده است. از توضیحات بالا نشان دادیم که ضریب اصطکاک جنبشی برابر با نسبت نیروی نخ به نیروی عمود بر سطح برای حالتی است که جسم روی سطح افقی با سرعت ثابت حرکت میکند.
آزمایش را برای حالت افقی و با توجه به جرمهای مختلف روی سطح افقی شش بار و در هر حالت سه بار تکرار کردیم. نتایج این بررسیها در جدول زیر نمایش داده شده است:
| جرم روی سطح افقی | نیروی عمود بر سطح | نیروی کشش نخ | ضریب اصطکاک جنبشی | ||||||||||||
|
|
| ||||||||||||||
|
|
| ||||||||||||||
|
|
| ||||||||||||||
|
|
| ||||||||||||||
|
|
| ||||||||||||||
|
| ||||||||||||||
میانگین ضریب اصطکاک جنبشی با در نظر گرفتن تمام حالتها برای سطح برابر با به دست میآید. غیر از روش هایی که برای محاسبه خطای آزمایش اصطکاک در بالا گفتیم میتوانیم نمودار دادهها را رسم کرده و ضریب اصطکاک جنبشی را از طریق شیب نمودار مقادیر نیروی کشش نخ در راستای عمودی و نیروی عمود بر سطح در راستای افقی به دست آوریم. نمودار در شکل زیر نمایش داده شده است. برای رسم خط بر روی دادهها خطی را در نظر میگیریم که بیشترین دادهها را در هر سری در برگیرد.

با توجه به دادههای نمودار سه مقدار برای سه شیب خط با توجه به دادهها به دست میآید که به ترتیب برابر با ، و است. با توجه به میانگینی که از آزمایش به دست آوردیم خطای نسبی برابر است:
بدین ترتیب خطای آزمایش اصطکاک برای ضریب اصطکاک جنبشی برابر با به دست میآید.
معرفی فیلم آموزش فیزیک پایه 1
مجموعه فرادرس در تولید و تهیه محتوای آموزشی خود اقدام به تهیه فیلم آموزش فیزیک پایه ۱ کرده است. این مجموعه آموزشی از سیزده درس تشکیل شده و برای دانشجویان رشتههای علوم پایه و فنی و مهندسی مفید است. پیشنیاز این درس آموزش ریاضی عمومی ۱ است. این آموزش جزو اولین دروس دانشگاهی است که شامل مفاهیم مربوط به فیزیک عمومی است و اگر شما در مفاهیم ابتدایی فیزیک دچار مشکل هستید، پیشنهاد میکنیم از این آموزش شروع کنید و سپس مجموعههای دیگر مربوط به فیزیک را مشاهده کنید.
درس اول این مجموعه به اندازه گیری و یکاها و درس دوم به قوانین بردارها میپردازد. درس سوم به حرکت در یک بُعد و درس چهارم به حرکت در دو و سه بُعد اختصاص دارد. در درس پنجم و ششم به ترتیب دینامیک حرکت و کاربرد قوانین نیوتن و کار و انرژی را خواهید آموخت و در درس هفتم مفاهیم مربوط به پایستگی انرژی و انرژی پتانسیل بررسی میشود. در درس هشتم درباره تکانه و برخورد خواهید آموخت و درس نهم به مرکز جرم و سیستمهای ذرات اختصاص دارد. درس دهم و یازدهم مباحث مربوط به سینماتیک و دینامیک دورانی را پوشش میدهد و درس دوازدهم و سیزدهم به مفاهیم مربوط به تکانه زاویهای و تعادل اختصاص دارد.
- برای دیدن آموزش فیزیک پایه ۱ + اینجا کلیک کنید.
آموزش فیزیک پایه ۱ (مرور و حل تست)
مجموعه فرادرس در تولید و تهیه محتوای آموزشی خود اقدام به تهیه فیلم آموزش فیزیک پایه ۱ (مرور و حل تست)
برای دانشجویان علوم پایه و فنی و مهندسی کرده است. این مجموعه آموزشی از بیست و سه درس تشکیل شده و برای دانشجویان رشته علوم پایه و فنی مهندسی مفید است. پیشنیاز این درس آموزش فیزیک پایه ۱، ریاضی ۱ و معادلات دیفرانسیل است.
درس اول، دوم و سوم این مجموعه به ترتیب به مقدمه ای بر فیزیک پایه ۱ که شامل اندازهگیری و محاسبه خطا در اندازهگیری است و حرکت شناسی اختصاص دارد. درس چهارم، پنجم، ششم و هفتم در چهار بخش در مورد دینامیک سیستمهای تک ذرهای صحبت خواهد کرد و درس هشتم، نهم و دهم به مفهوم دینامیک سیستمهای بس ذرهای میپردازد. درس یازدهم، دوزادهم، سیزدهم و چهاردهم به حرکت دورانی اختصاص دارد. درس پانزدهم و شانردهم به آموزش تعادل دینامیکی میپردازد. در درسهای هفدهم، هجدهم، نوزدهم و بیستم مفهوم کار و انرژی را خواهید آموخت. در نهایت پایان بخش این مجموعه آموزشی سه درس مربوط به آموزش نوسان است.
- برای دیدن آموزش فیزیک پایه ۱ (مرور و حل تست) + اینجا کلیک کنید.
معرفی فیلم آموزش فیزیک ۱ دانشگاهی با رویکرد حل مساله
مجموعه فرادرس در تولید و تهیه محتوای آموزشی خود اقدام به تهیه فیلم آموزش فیزیک ۱ دانشگاهی با رویکرد حل مساله کرده است. این مجموعه آموزشی از هفت درس تشکیل شده و برای دانشجویان رشتههای علوم پایه و مهندسی است.
درس اول این مجموعه به اندازه گیری و درس دوم به محاسبات برداری میپردازد. درس سوم حرکت یک بعدی و درس چهارم حرکت در دو بعد را بررسی میکند. در درس پنجم و ششم به ترتیب دینامیک و کار و انرژی را خواهید آموخت و در درس هفتم مفاهیم مربوط به گرما و دما (ترمودینامیک) بررسی میشود.
- برای دیدن آموزش فیزیک ۱ دانشگاهی با رویکرد حل مساله + اینجا کلیک کنید.
جمعبندی
در این مطلب در مورد محاسبه خطای آزمایش اصطکاک صحبت میکنیم. بدین منظور ابتدا در مورد انواع نیروها و ویژگیهای آن صحبت کردیم. سپس انواع نیروهای اصطکاک را معرفی میکنیم و روشهای متفاوت انجام آزمایش اصطکاک را توضیح دادیم. در نهایت یک نمونه مثال عددی در محاسبه خطای آزمایش اصطکاک را ارائه دادیم.













درود بر شما.مقاله اتون جامع و کامل بود.سپاسگزارم
سلامت و بهروز باشید.