نسبت های مثلثاتی به زبان ساده + مثال و تمرین

نسبت های مثلثاتی، توابعی هستند که رابطه بین اندازه ضلع‌ها و زاویه‌های مثلث قائم‌الزاویه را نمایش می‌دهند. نکته جالب در مورد این نسبت‌ها، کاربردهای گسترده آن‌ها در حوزه‌های مختلف است. نسبت‌های مثلثاتی در حوزه‌های مختلفی نظیر نجوم، مسیریابی، ساخت تجهیزات صوتی، زیست‌شناسی دریا، هوافضا، ساخت و تولید، پزشکی، تحقیقات جنایی و غیره کاربرد دارند. از شناخته شده‌ترین نسبت‌های مثلثاتی می‌توان به توابع سینوس، کسینوس، تانژانت، کتانژانت، کسکانت و سکانت، اشاره کرد. در این مقاله، قصد داریم ضمن تعریف نسبت های مثلثاتی، به معرفی برخی از مهم‌ترین روابط بین این نسبت‌ها به همراه حل چند مثال بپردازیم.

نسبت های مثلثاتی چه هستند ؟

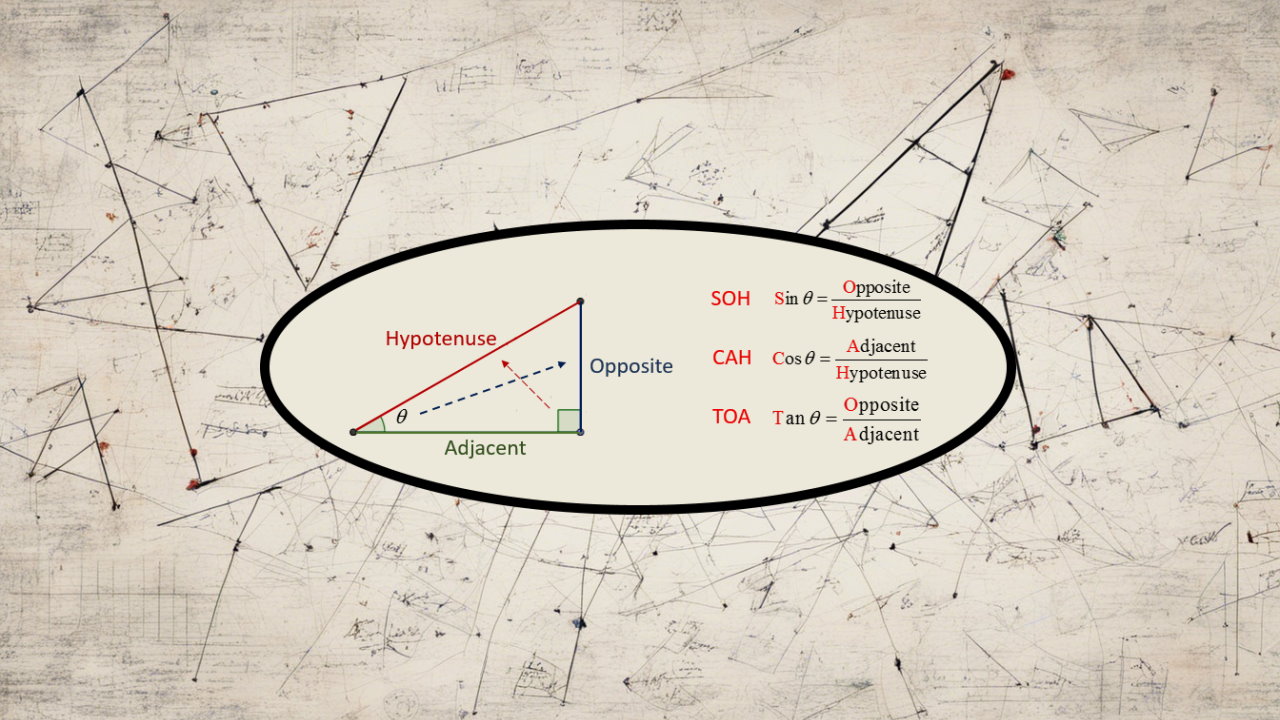
نسبت‌های مثلثاتی، توابعی هستند که رابطه بین زوایای داخلی مثلث قائم‌الزاویه با نسبت ضلع‌های آن به یکدیگر را نمایش می‌دهند. به نسبت های مثلثاتی، توابع مثلثاتی یا روابط مثلثاتی نیز می‌گویند. سینوس، کسینوس و تانژانت، به عنوان نسبت های مثلثاتی اصلی در نظر گرفته می‌شوند.

برای تعریف این نسبت‌ها، مثلث قائم‌الزاویه زیر را در نظر بگیرید.

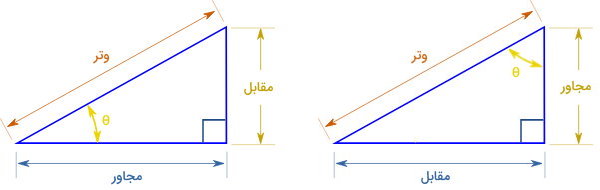
مثلث‌های قائم‌الزاویه، از یک زاویه راست (زاویه قائمه یا زاویه ۹۰ درجه) تشکیل می‌شوند. به ضلع مقابل به این زاویه، وتر می‌گویند. دو ضلع دیگر (ضلع‌های به وجود آورنده زاویه راست)، ساق نام دارند. نسبت های مثلثاتی، با توجه به دو زاویه غیرقائمه و ضلع‌های مقابل و مجاور به آن‌ها نوشته می‌شوند.

سینوس

یکی از مهم‌ترین توابع مثلثاتی، تابع سینوس (Sine) است. بر اساس زاویه مورد نظر (زاویه غیرقائمه θ) در مثلث قائم‌الزاویه، این تابع به صورت نسبت ضلع مقابل به وتر تعریف می‌شود:

وتر ÷ ضلع مقابل زاویه θ = سینوس زاویه θ

$$\sin { \theta } = \frac { O }{ H }$$

• $$\sin { \theta }$$: سینوس زاویه θ
• O: ضلع مقابل زاویه θ
• H: وتر مثلث قائم‌الزاویه

کسینوس

دومین تابع مثلثاتی اصلی، کسینوس (Cosine) است. کسینوس زاویه θ در مثلث قائم‌الزاویه، از تقسیم ضلع مجاور θ به وتر به دست می‌آید:

وتر ÷ ضلع مجاور زاویه θ = کسینوس زاویه θ

$$\cos { \theta } = \frac { A }{ H }$$

• $$\cos { \theta }$$: کسینوس زاویه θ
• A: ضلع مجاور زاویه θ
• H: وتر مثلث قائم‌الزاویه

تانژانت

تانژانت (Tangent)، یکی از دیگر توابع مثلثاتی اصلی و شناخته شده است. این تابع، نسبت ضلع مقابل به مجاور زاویه θ در مثلث قائم‌الزاویه را نمایش می‌دهد:

ضلع مجاور زاویه θ ÷ ضلع مقابل زاویه θ = تانژانت زاویه θ

$$\tan { \theta } = \frac { O }{ A }$$

• $$\tan { \theta }$$: تانژانت زاویه θ
• O: ضلع مقابل زاویه θ
• A: ضلع مجاور زاویه θ

تانژانت زاویه θ، از تقسیم سینوس θ بر کسینوس θ به دست می‌آید. با تقسیم عبارت‌های این نسبت های مثلثاتی می‌توانید فرمول بالا را اثبات کنید.

سینوس، کسینوس و تانژانت، نسبت های مثلثاتی اصلی هستند. علاوه بر این توابع، نسبت‌های دیگری وجود دارند که در ادامه به معرفی آن‌ها می‌پردازیم.

کتانژانت

کتانژانت (Cotangent)، نسبت ضلع مجاور به ضلع مقابل زاویه θ در مثلث قائم‌الزاویه را نمایش می‌دهد. این تابع، نسبت کسینوس به سینوس است. فرمول کتانژانت زاویه θ به صورت زیر نوشته می‌شود:

ضلع مقابل زاویه θ ÷ ضلع مجاور زاویه θ = تانژانت زاویه θ

$$\cot { \theta } = \frac { A }{ O }$$

• $$\cot { \theta }$$: کتانژانت زاویه θ
• A: ضلع مجاور زاویه θ
• O: ضلع مقابل زاویه θ

بسیاری، تابع کتانژانت را به عنوان یکی از نسبت های مثلثاتی اصلی در نظر می‌گیرند. این تابع، عکس تابع تانژانت است. به همین دلیل، با محاسبه تانژانت، محاسبه کتانژانت نیز به سادگی انجام می‌شود.

کسکانت

کسکانت (Cosecant)، یکی دیگر از نسبت های مثلثاتی است که نسبت وتر به ضلع مقابل زاویه θ در مثلث قائم‌الزاویه را نمایش می‌دهد. این تابع به صورت زیر تعریف می‌شود:

ضلع مقابل زاویه θ ÷ وتر = کسکانت زاویه θ

$$\csc { \theta } = \frac { H }{ O }$$

• $$\csc { \theta }$$: کسکانت زاویه θ
• H: وتر مثلث قائم‌الزاویه
• O: ضلع مقابل زاویه θ

بر اساس تعریف کسکانت، این تابع را می‌توان عکس سینوس در نظر گرفت.

سکانت

سکانت (Secant)، نسبت وتر به ضلع مجاور زاویه θ در مثلث قائم‌الزاویه است. این نسبت مثلثاتی، با عکس کسینوس زاویه θ برابری می‌کند. ساکانت θ از رابطه زیر به دست می‌آید:

ضلع مجاور زاویه θ ÷ وتر = کسکانت زاویه θ

$$\sec { \theta } = \frac { H }{ A }$$

• $$\sec { \theta }$$: کسکانت زاویه θ
• H: وتر مثلث قائم‌الزاویه
• A: ضلع مجاور زاویه θ

برخی از روابط بین توابع مثلثاتی

فرمول‌های زیادی برای نمایش رابطه بین توابع مثلثاتی مختلف وجود دارند. به عنوان مثال، یکی از معروف‌ترین و مهم‌ترین فرمول‌های مثلثاتی عبارت است از:

$$\sin ^ ۲ \theta + \cos ^ ۲ \theta = ۱$$

این فرمول، با عنوان قضیه فیثاغورس در مثلثات شناخته می‌شود و رابطه بین مربع سینوس و مربع کسینوس یک زاویه را نمایش می‌دهد. از دیگر روابط مهم بین توابع مثلثاتی می‌توان به موارد زیر اشاره کرد:

$$۱ + \tan ^ ۲ \theta = \sec ^ ۲$$

$$۱ + \cot ^ ۲ \theta = \csc ^ ۲$$

در بخش‌های بعدی، به معرفی روابط بیشتری خواهیم پرداخت.

جدول رابطه بین نسبت های مثلثاتی

در بخش‌های قبلی دیدیم که نسبت های مثلثاتی، با یکدیگر رابطه دارند. به عبارت دیگر، نسبت های مثلثاتی را می‌توان بر حسب یکدیگر بازنویسی کرد.

جدول زیر، رابطه بین سینوس، کسینوس، تانژانت، کتانژانت، سکانت و کسکانت را نمایش می‌دهد.

جدول مقادیر نسبت های مثلثاتی زوایای خاص

در مثلثات، زاویه‌های ۰، ۳۰، ۴۵، ۶۰ و ۹۰ درجه، به عنوان زوایه‌های خاص شناخته می‌شوند. جدول زیر، مقادیر نسبت‌های مثلثاتی برای این زاویه‌ها را نمایش می‌دهد.

مقادیر مربوط به توابع مثلثاتی دیگر زوایای پرکاربرد، در جدولی موسوم به جدول سینوس کسینوس آورده می‌شوند.

تعیین علامت نسبت های مثلثاتی در دایره مثلثاتی

دایره مثلثاتی، یک دایره به شعاع واحد (۱) است که امکان محاسبه نسبت های مثلثاتی، تعیین علامت و اثبات روابط بین آن‌ها را فراهم می‌کند.

این دایره، معمولا به چهار قسمت مساوی یا تقسیم می‌شوند. سینوس، کسینوس، تانژانت و کتانژانت در هر یک از این ربع‌ها، دارای علامت مشخصی هستند.

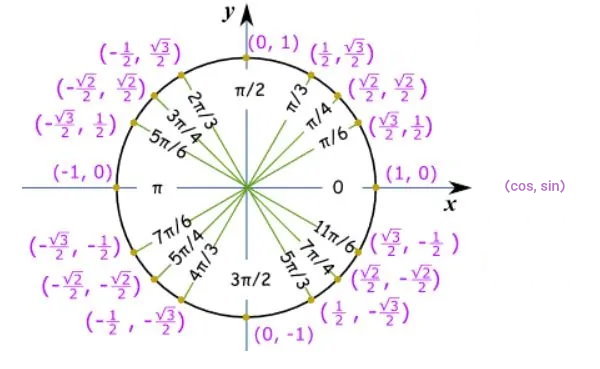
در بخش قبلی، به معرفی مقدار عددی نسبت‌های مثلثاتی برخی از زاویه‌ها پرداختیم. این زاویه‌ها، بین ۰ تا ۹۰ درجه یا اصطلاحا در ربع اول دایره مثلثاتی قرار داشتند. تمام نسبت‌های مثلثاتی، در ربع اول دارای علامت مثبت هستند. اما این مسئله برای ربع‌های دیگر صادق نیست. علامت نسبت های مثلثاتی در چهار ربع دایره واحد به صورت زیر تعیین می‌شود:

• ربع اول: در بازه ۰ تا ۹۰ درجه یا ۰ تا π/۲، علامت همه نسبت‌های مثلثاتی مثبت است.
• ربع دوم: در بازه ۹۰ تا ۱۸۰ درجه یا ۰ تا π، علامت سینوس مثبت و علامت بقیه منفی نسبت‌های مثلثاتی منفی است.
• ربع سوم: در بازه ۱۸۰ تا ۲۷۰ درجه یا π- تا π/۲-، علامت تانژانت و کتانژانت مثبت، علامت سینوس و کسینوس منفی است.
• ربع چهارم: در بازه ۲۷۰ تا ۳۶۰ درجه یا π/۲- تا ۰، علامت کسینوس مثبت و علامت بقیه نسبت‌های مثلثاتی منفی است.

جدول زیر، تعیین علامت نسبت‌های مثلثاتی را در بازه‌های مختلف نمایش می‌دهد.

نسبت های مثلثاتی معکوس

معکوس توابع یا توابع معکوس، توابعی هستند که با جابجا کردن جای پارامترهای ورودی و خروجی به وجود می‌آیند. به عنوان مثال، تابع سینوس را در نظر بگیرید:

$$\sin { \theta } = \frac { O }{ H }$$

در این تابع، با قرار دادن مقدار زاویه θ، نسبت ضلع مقابل به وتر به دست می‌آید. اکنون، اگر تابعی داشته باشیم که با قرار دادن مقدار نسبت ضلع مقابل به وتر، به مقدار زاویه θ برسیم، به آن، معکوس تابع سینوس می‌گوییم و آن را با $$\sin ^ { - ۱ }$$ نمایش می‌دهیم:

$$\sin ^ { - ۱ } { ( \frac { O }{ H } ) } = \theta$$

معکوس دیگر نسبت های مثلثاتی نیز به همین صوت تعریف می‌شود. به این ترتیب داریم:

$$\cos ^ { - ۱ } { ( \frac { A }{ H } ) } = \theta$$

$$\tan ^ { - ۱ } { ( \frac { O }{ A } ) } = \theta$$

$$\cot ^ { - ۱ } { ( \frac { A }{ O } ) } = \theta$$

معکوس توابع مثلثاتی با پیشوند «آرک» (Arc) نیز بیان می‌شوند:

• معکوس سینوس: آرک سینوس (Arcsine)
• معکوس کسینوس: آرک کسینوس (Arccosine)
• معکوس تانژانت: آرک تانژانت (Arctangent)
• معکوس تانژانت: آرک کتانژانت (Arccotangent)

مثال ۱: محاسبه زاویه با استفاده از معکوس سینوس

اندازه ضلع مقابل به زاویه حاده α در یک مثلث قائم‌الزاویه برابر با x و اندازه وتر مثلث برابر با ۲x است. مقدار زاویه θ را به دست بیاورید.

در این مثال، می‌خواهیم از طول ضلع‌ها به اندازه زاویه برسیم. برای این کار، به روابط معکوس توابع مثلثاتی نیاز داریم. به دلیل مشخص بودن اندازه وتر و ضلع مقابل به زاویه مورد نظر، فرمول معکوس تابع سینوس را می‌نویسیم:

$$\sin ^ { - ۱ } { ( \frac { O }{ H } ) } = \theta$$

• $$\sin ^ { - ۱ }$$: معکوس سینوس
• H: وتر مثلث قائم‌الزاویه برابر با ۲x
• O: ضلع مقابل زاویه θ برابر با x

پارامترهای داده شده در صورت سوال را درون فرمول بالا قرار می‌دهیم:

$$\sin ^ { - ۱ } { ( \frac { x }{ ۲x } ) } = \theta$$

$$\sin ^ { - ۱ } { ( \frac { ۱ }{ ۲ } ) } = \theta$$

با توجه به رابطه به دست آمده، مقدار زاویه θ، برابر با معکوس تابع سینوس در نقطه یک‌دوم است. به این ترتیب، باید ببینیم سینوس کدام زاویه برابر با یک‌دوم می‌شود. سینوس زاویه ۳۰ درجه برابر با یک‌دوم است:

$$\sin { ۳۰ ^ { \circ } } = \frac { ۱ }{ ۲ }$$

بنابراین:

$$\sin ^ { - ۱ } { ( \frac { ۱ }{ ۲ } ) } = ۳۰ ^ { \circ }$$

$$\sin ^ { - ۱ } { ( \frac { ۱ }{ ۲ } ) } = \frac { \pi }{ ۶ }$$

در نتیجه، مقدار زاویه θ برابر با ۳۰ درجه است.

نسبت های مثلثاتی قرینه زاویه

قرینه عدد، حاصلضرب آن عدد در منفی یک (۱-) است. به عبارت دیگر، قرینه هر عدد، همان عدد با علامت منفی است. در مثلثات، اگر بخواهیم نسبت های مثلثاتی قرینه یک زاویه را به دست بیاوریم، می‌توانیم با استفاده از یک‌سری روابط، آن‌ها را به نسبت‌های مثلثاتی معمولی تبدیل کنیم.

برخی از این روابط عبارت هستند از:

$$\sin ( { - \theta } ) = - \sin { \theta }$$

$$\cos ( { - \theta } ) = \cos { \theta }$$

$$\tan ( { - \theta } ) = - \tan { \theta }$$

$$\cot ( { - \theta } ) = - \cot { \theta }$$

$$\sec ( { - \theta } ) = \sec { \theta }$$

$$\csc ( { - \theta } ) = - \csc { \theta }$$

مثال ۲: محاسبه کسینوس زاویه منفی

کسینوس زاویه ۴۵- درجه را به دست بیاورید.

بر اساس روابط ارائه شده برای نسبت های مثلثاتی قرینه یک زاویه، داریم:

$$\cos ( { - \theta } ) = \cos { \theta }$$

این رابطه را با توجه به زاویه مورد سوال بازنویسی می‌کنیم:

$$\cos ( { - ۴۵ ^ { \circ } } ) = \cos { ۴۵ ^ { \circ } }$$

کسینوس ۴۵ برابر است با:

$$\cos { ۴۵ ^ { \circ } } = \frac { \sqrt { ۲ } }{ ۲ }$$

بنابراین، کسینوس ۴۵- درجه برابر خواهد بود با:

$$\cos ( { - ۴۵ ^ { \circ } } ) = \frac { \sqrt { ۲ } }{ ۲ }$$

نسبت های مثلثاتی زوایای متمم

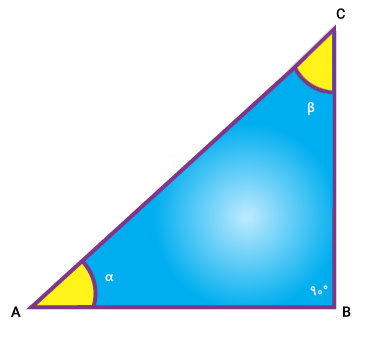
به زوایایی که مجموع آن‌ها برابر با ۹۰ درجه می‌شود، زوایای مکمل می‌گویند. مثلث قائم‌الزاویه زیر را در نظر بگیرید.

با توجه به جمع زوایای داخلی مثلث (۱۸۰ درجه)، جمع دو زاویه α و β برابر با ۹۰ درجه است.

یک زاویه فرضی مانند θ را در نظر بگیرید. متمم این زاویه برابر است با:

۹۰° = متمم زاویه θ + زاویه θ

$$۹۰ ^ { \circ } - \theta$$ = متمم زاویه θ

روابط مثلثاتی متمم زاویه θ به صورت زیر نوشته می‌شوند:

$$\sin { ( ۹۰ ^ { \circ } - \theta ) } = \cos { \theta }$$

$$\cos { ( ۹۰ ^ { \circ } - \theta ) } = \sin { \theta }$$

$$\tan { ( ۹۰ ^ { \circ } - \theta ) } = \cot { \theta }$$

$$\cot { ( ۹۰ ^ { \circ } - \theta ) } = \tan { \theta }$$

$$\csc { ( ۹۰ ^ { \circ } - \theta ) } = \sec { \theta }$$

$$\sec { ( ۹۰ ^ { \circ } - \theta ) } = \csc { \theta }$$

رابطه بین α و β در مثلث ABC‌ عبارت است از:

$$\alpha + \beta = ۹۰ ^ { \circ }$$

$$\beta = ۹۰ ^ { \circ } - \alpha$$

$$\alpha = ۹۰ ^ { \circ } - \beta$$

بنابراین، با داشتن هر یک از زوایای متمم α یا β، می‌توانیم مقدار نسبت‌های مثلثاتی زاویه دیگر را به دست بیاوریم. به عبارت دیگر:

$$\sin { \beta } = \cos { \alpha}$$

$$\cos { \beta } = \sin { \alpha}$$

$$\tan { \beta } = \cot { \alpha}$$

$$\cot { \beta } = \tan { \alpha}$$

$$\csc { \beta } = \sec { \alpha}$$

$$\sec { \beta } = \csc { \alpha}$$

در بسیاری از منابع مرتبط با مبحث مثلثات، زاویه‌ها بر حسب رادیان بیان می‌شوند. بنابراین، معمولا نمایش متمم یک زاویه مشابه عبارت $$\frac { \pi }{ ۲ } - \theta$$ خواهد بود.

 مثال ۳: محاسبه تانژانت متمم یک زاویه

دو زاویه α و β، متمم یکدیگرند. اگر مقدار زاویه α برابر با ۶۰ درجه باشد، تانژانت زاویه β چقدر است؟

برای به دست آوردن تانژانت β، دو روش داریم.

روش اول

از آنجایی که α و β، متمم هستند، جمع آن‌ها برابر با ۹۰ درجه می‌شود:

$$\alpha + \beta = ۹۰ ^ { \circ }$$

زاویه α برابر با ۶۰ درجه است. بنابراین:

$$۶۰ ^ { \circ } + \beta = ۹۰ ^ { \circ }$$

$$\beta = ۹۰ ^ { \circ } - ۶۰ ^ { \circ }$$

$$\beta = ۳۰ ^ { \circ }$$

زاویه β برابر با ۳۰ درجه است. اکنون می‌توانیم تانژانت زاویه ۳۰ درجه را محاسبه کنیم.

روش دوم

α و β، متمم هستند. بنابراین، تانژانت β، برابر با کتانژانت α می‌شود:

$$\tan { \beta } = \cot { \alpha}$$

$$\tan { \beta } = \cot { ۶۰ ^ { \circ } }$$

کتانژانت زاویه ۶۰ درجه از تقسیم کسینوس زاویه ۶۰ درجه بر سینوس زاویه ۶۰ درجه به دست می‌آید:

$$\cot { ۶۰ ^ { \circ } } = \frac { \cos ۶۰ ^ { \circ } }{ \sin ۶۰ ^ { \circ } }$$

با توجه به جدول نسبت های مثلثاتی برای زوایای خاص، داریم:

$$\cos ۶۰ ^ { \circ } = \frac { ۱ }{ ۲ }$$

$$\sin ۶۰ ^ { \circ } = \frac { \sqrt { ۳ } }{ ۲ }$$

این مقادیر را درون رابطه تانژانت قرار می‌دهیم:

$$\cot { ۶۰ ^ { \circ } } = \frac { \frac { ۱ }{ ۲ } }{ \frac { \sqrt { ۳ } }{ ۲ } }$$

$$\cot { ۶۰ ^ { \circ } } = \frac { ۱ }{ \sqrt { ۳ } }$$

بنابراین، تانژانت زاویه β (تانژانت زاویه ۳۰ درجه) برابر با $$\sqrt { ۳ }$$ است.

مثال ۴: محاسبه تانژانت جمع یک زاویه با زاویه قائمه

تانژانت جمع زاویه α با $$\frac { \pi }{ ۲ }$$ را به دست بیاورید.

صورت سوال، حاصل عبارت زیر را از ما می‌خواهد:

$$\tan { ( \frac { \pi }{ ۲ } + \alpha ) }$$

$$\frac { \pi }{ ۲ }$$، همان زاویه ۹۰ درجه است. بنابراین می‌توانیم رابطه بالا را به صورت زیر بنویسیم:

$$\tan { ( ۹۰ ^ { \circ } + \alpha ) }$$

در این بخش با فرمول کلی رابطه نسبت‌های مثلثاتی زوایای متمم آشنا شدیم. اکنون، رابطه بالا را به شکل این فرمول درمی‌آوریم:

$$\tan { [ ۹۰ ^ { \circ } - ( - \alpha) ] }$$

می‌دانیم که رابطه تانژانت زاویه متمم عبارت است از:

$$\tan { ( ۹۰ ^ { \circ } - \theta ) } = \cot { \theta }$$

به جای θ، عبارت α- را قرار می‌دهیم:

$$\tan { [ ۹۰ ^ { \circ } - (- \alpha )] } = \cot { ( - \alpha ) }$$

بنابراین:

$$\tan { ( ۹۰ ^ { \circ } + \alpha )} = \cot { ( - \alpha ) }$$

از بخش نسبت های مثلثاتی قرینه زاویه می‌دانیم:

$$\cot ( { - \theta } ) = - \cot { \theta }$$

در نتیجه:

$$\tan { ( ۹۰ ^ { \circ } + \alpha )} = \cot { ( - \alpha ) } = - \cot { \theta }$$

$$\tan { ( ۹۰ ^ { \circ } + \alpha )}= - \cot { \theta }$$

$$\tan { ( \frac { \pi }{ ۲ } + \alpha )}= - \cot { \theta }$$

تانژانت جمع زاویه α با $$\frac { \pi }{ ۲ }$$ برابر با منفی کتانژانت زاویه α است.

نسبت های مثلثاتی زوایای مکمل

اگر جمع دو زاویه برابر با ۱۸۰ درجه (زاویه نیم‌صفحه) شود، به آن‌ها زوایای مکمل می‌گویند. نسبت‌های مثلثاتی این زوایا را می‌توان نسبت به یکدیگر بازنویسی کرد.

به عنوان مثال، در صورت داشتن زاویه θ، نسبت‌های مثلثاتی مکمل آن با استفاده از روابط زیر به دست می‌آیند:

$$\sin { ( ۱۸۰ ^ { \circ } - \theta ) } = \sin{ \theta }$$

$$\cos { ( ۱۸۰ ^ { \circ } - \theta ) } = - \cos{ \theta }$$

$$\tan { ( ۱۸۰ ^ { \circ } - \theta ) } = - \tan { \theta }$$

$$\cot { ( ۱۸۰ ^ { \circ } - \theta ) } = - \cot { \theta }$$

$$\csc { ( ۱۸۰ ^ { \circ } - \theta ) } = \csc{ \theta }$$

$$\sec { ( ۱۸۰ ^ { \circ } - \theta ) } = - \sec{ \theta }$$

دو زاویه α و β را در نظر بگیرید. با فرض مکمل بودن این زوایا، خواهیم داشت:

$$\alpha + \beta = ۱۸۰ ^ { \circ }$$

$$\alpha = ۱۸۰ ^ { \circ } - \beta$$

$$\beta = ۱۸۰ ^ { \circ } - \alpha$$

به این ترتیب، رابطه بین نسبت های مثلثاتی این دو زاویه به صورت زیر نوشته می‌شود:

$$\sin { \beta } = \sin{ \alpha }$$

$$\cos { \beta } = - \cos{ \alpha }$$

$$\tan { \beta } = - \tan { \alpha }$$

$$\cot { \beta } = - \cot { \alpha }$$

$$\csc { \beta } = \csc{ \alpha }$$

$$\sec { \beta } = - \sec{ \alpha }$$

معمولا نمایش مکمل یک زاویه در مسائل مثلثات، مشابه عبارت $$\pi - \theta$$ خواهد بود. همانطور که مشاهده می‌کنید، نسبت‌های مثلثاتی مکمل یک زاویه، با نسبت‌های مثلثاتی همان زاویه تفاوتی ندارد و فقط در برخی از روابط، علامت آن‌ها با یکدیگر فرق می‌کند.

مثال ۵: محاسبه کسکانت مکمل یک زاویه

کسکانت زاویه ۷۵ درجه برابر با ۱/۰۴ است. با در نظر داشتن این مقدار، کسکانت زاویه ۱۰۵ درجه را به دست بیاورید.

مجموع زوایای ۷۵ و ۱۰۵ درجه، برابر با ۱۸۰ درجه می‌شود. از این‌رو، این دو زاویه، مکمل یکدیگرند. بین کسکانت دو زاویه مکمل، رابطه زیر برقرار است:

$$\csc { \beta } = \csc{ \alpha }$$

بنابراین:

$$\csc { ۱۰۵ ^ { \circ } } = \csc{ ۷۵ ^ { \circ } }$$

$$\csc { ۱۰۵ ^ { \circ } } = ۱/۰۴$$

در نتیجه، کسکانت زاویه ۱۰۵ درجه نیز برابر با ۱/۰۴ است.

نسبت های مثلثاتی زوایای انتقال یافته

اگر زاویه‌ای مانند θ را به اندازه یک دوره تناوب، نصف دوره تناوب یا ربع دوره تناوب نسبت‌های مثلثاتی جابجا کنیم، امکان نوشتن روابط مثلثاتی زاویه جدید بر حسب θ فراهم می‌شود. در بخش‌های قبلی (نسبت‌های مثلثاتی زوایای متمم و مکمل)، با برخی از این روابط آشنا شدیم. جدول زیر، برخی دیگر از روابط نسبت های مثلثاتی زوایای دوران یافته را نمایش می‌دهد.

مثال ۶: محاسبه کتانژانت زاویه دوران یافته

کتانژانت زاویه‌ای برابر با ۰/۵۱ است. اگر این زاویه را به اندازه ۴۵ درجه در جهت حرکت عقربه‌های ساعت دوران دهیم، مقدار کتانژانت چقدر می‌شود.

۴۵ درجه، برابر با ربع یا یک‌چهارم دایره مثلثاتی است. کتانژانت زاویه دوران‌یافته به اندازه ۴۵ درجه از رابطه زیر به دست می‌آید:

$$\cot { ( \theta \pm \frac { \pi }{ ۴ } ) } = \frac { \cot \theta \mp ۱ }{ ۱ \pm \cot \theta }$$

عبارت معرف زاویه در سمت چپ رابطه بالا، دارای علامت مثبت-منفی است. تعیین این علامت، به جهت جابجایی زاویه (جابجایی ساعتگرد یا پادساعتگرد) بستگی دارد. در دایره مثلثاتی، حرکت پادساعتگرد (خلاف جهت حرکت عقربه‌های ساعت)، یک جابجایی مثبت و حرکت ساعتگرد (جهت حرکت عقربه‌های ساعت)، یک جابجایی منفی در نظر گرفته می‌شود. بنابراین، مطابق با صورت سوال، باید رابطه دارای علامت منفی را مورد استفاده قرار دهیم. این رابطه عبارت است از:

$$\cot { ( \theta - \frac { \pi }{ ۴ } ) } = \frac { \cot \theta + ۱ }{ ۱ - \cot \theta }$$

زاویه درون تابع کتانژانت در سمت چپ رابطه، جابجایی ۴۵ درجه‌ای زاویه θ در جهت ساعتگرد را نمایش می‌دهد. با توجه به عبارت‌های سمت راست رابطه، برای محاسبه این $$\cot { ( \theta - \frac { \pi }{ ۴ } ) }$$، به مقدار $$\cot { \theta }$$ نیاز داریم. کتانژانت θ برابر با ۰/۵۱ است. این مقدار را درون رابطه اصلی قرار می‌دهیم:

$$\cot { ( \theta - \frac { \pi }{ ۴ } ) } = \frac { ۰/۵۱ + ۱ }{ ۱ - ۰/۵۱ } = ۳/۰۸$$

در نتیجه، کتانژانت زاویه مورد نظر، در صورت جابجایی ۴۵ درجه‌ای در جهت حرکت عقربه‌های ساعت، برابر با ۳/۰۸۱ می‌شود.

نسبت های مثلثاتی جمع و تفریق دو زاویه

دو زاویه مانند α و β را در نظر بگیرید. اگر بخواهیم نسبت‌های مثلثاتی جمع این دو زاویه را به دست بیاوریم، از روابط زیر استفاده می‌کنیم:

$$\sin ( \alpha + \beta ) = \sin \alpha \cos \beta + \cos \alpha \sin \beta$$

$$\cos ( \alpha + \beta ) = \cos \alpha \cos \beta − \sin \alpha \sin \beta$$

$$\tan ( \alpha + \beta ) = \frac { \tan { \alpha } + \tan { \beta } } { ۱ - \tan { \alpha } \tan { \beta }}$$

$$\cot ( \alpha + \beta ) = \frac { \cot { \alpha } \cot { \beta } - ۱ } { \cot { \alpha } + \cot { \beta } }$$

با توجه به روابط بالا می‌توانیم نسبت‌های مثلثاتی تفریق دو زاویه را به دست بیاوریم. به این منظور، کافی است عبارت تفریقی $$\alpha - \beta$$ را به صورت عبارت جمعی $$\alpha + ( - \beta )$$ بازنویسی کرده و از روابط معرفی شده در بخش نسبت های مثلثاتی قرینه زاویه (زاویه منفی) استفاده کنیم. با این کار، به روابط زیر خواهیم رسید:

$$\sin ( \alpha - \beta ) = \sin \alpha \cos \beta - \cos \alpha \sin \beta$$

$$\cos ( \alpha - \beta ) = \cos \alpha \cos \beta + \sin \alpha \sin \beta$$

$$\tan ( \alpha - \beta ) = \frac { \tan { \alpha } - \tan { \beta } } { ۱ + \tan { \alpha } \tan { \beta }}$$

$$\cot ( \alpha - \beta ) = \frac { \cot { \alpha } \cot { \beta } + ۱ } { \cot { \alpha } - \cot { \beta } }$$

مثال ۷: محاسبه سینوس جمع دو زاویه

سینوس زاویه ۱۲۰ درجه را با استفاده از فرمول نسبت های مثلثاتی جمع دو زاویه به دست بیاورید.

سینوس زاویه ۱۲۰ درجه، تقریبا برابر با ۰/۸۷ است. می‌خواهیم با استفاده از نسبت‌های مثلثاتی جمع دو زاویه، به این مقدار برسیم. به این منظور، دو زاویه α و β را در نظر بگیرد. اگر α برابر با ۳۰ درجه و β برابر با ۶۰ درجه باشد، جمع آن‌ها برابر با ۱۲۰ درجه می‌شود. رابطه سینوس جمع این دو زاویه عبارت است از:

$$\sin ( \alpha + \beta ) = \sin \alpha \cos \beta + \cos \alpha \sin \beta$$

مقدار زاویه‌ها را درون رابطه بالا قرار می‌دهیم:

$$\sin ( ۳۰ ^ { \circ } + ۶۰ ^ { \circ } ) = \sin ۳۰ ^ { \circ } \cos ۶۰ ^ { \circ } + \cos ۳۰ ^ { \circ } \sin ۶۰ ^ { \circ }$$

$$\sin ( ۱۲۰ ^ { \circ } ) = \sin ۳۰ ^ { \circ } \cos ۶۰ ^ { \circ } + \cos ۳۰ ^ { \circ } \sin ۶۰ ^ { \circ }$$

سینوس ۳۰ درجه برابر با $$\frac { ۱ } { ۲ }$$، سینوس ۶۰ درجه برابر با $$\frac { \sqrt { ۳ } } { ۲ }$$، کسینوس ۳۰ درجه برابر با  $$\frac { \sqrt { ۳ } } { ۲ }$$ و سینوس ۶۰ درجه برابر با $$\frac { ۱ } { ۲ }$$ است. این مقادیر را درون رابطه بالا قرار می‌دهیم:

$$\sin ( ۱۲۰ ^ { \circ } ) = ( \frac { ۱ } { ۲ } \times \frac { \sqrt { ۳ } } { ۲ } ) + ( \frac { \sqrt { ۳ } } { ۲ } \times \frac { ۱ } { ۲ } )$$

$$\sin ( ۱۲۰ ^ { \circ } ) = \frac { \sqrt { ۳ } } { ۴ } + \frac { \sqrt { ۳ } } { ۴ }$$

$$\sin ( ۱۲۰ ^ { \circ } ) = \frac { ۲ \sqrt { ۳ } } { ۴ }$$

$$\sin ( ۱۲۰ ^ { \circ } ) = \frac { \sqrt { ۳ } } { ۲ }$$

$$\sin ( ۱۲۰ ^ { \circ } ) = \frac { ۱/۷۳} { ۲ }$$

$$\sin ( ۱۲۰ ^ { \circ } ) \approx ۰/۸۷$$

به این ترتیب، با استفاده از فرمول سینوس جمع دو زاویه نیز به مقدار ۰/۸۷ برای سینوس زاویه ۱۲۰ درجه رسیدیم. همانطور که مشاهده می‌کنید، سینوس زاویه ۱۲۰ درجه با کسینوس زاویه ۳۰ درجه برابر است. در بخش نسبت‌های مثلثاتی انتقال یافته، فرمول زیر را معرفی کردیم:

$$\cos { ( \theta \pm ۹۰ ^ { \circ } ) } = \mp \sin \theta$$

رابطه بین سینوس زاویه ۱۲۰ درجه با کسینوس زاویه ۳۰ درجه، در این فرمول قابل مشاهده است:

$$\cos { ( ۱۲۰ ^ { \circ } - ۹۰ ^ { \circ } ) } = + \sin ۱۲۰ ^ { \circ }$$

$$\cos { ۳۰ ^ { \circ } } = \sin ۱۲۰ ^ { \circ }$$

نسبت های مثلثاتی دو برابر یک زاویه

زاویه θ را در نظر بگیرید. نسبت‌های مثلثاتی دو برابر زاویه θ زاویه (۲θ) با استفاده از روابط زیر به دست می‌‌آید:

$$\sin ( ۲ \theta ) = ۲ \sin \theta \cos \theta$$

$$\cos ( ۲ \theta ) = \cos ^ ۲ \theta - \sin ^ ۲ \theta$$

$$\tan ( ۲ \theta ) = \frac { ۲ \tan \theta } { ۱ - \tan ^ ۲ \theta }$$

$$\cot ( ۲ \theta ) = \frac { \cot ^ ۲ \theta - ۱ } { ۲ \cot \theta }$$

زاویه مضاعف را می‌توان به صورت جمع دو زاویه برابر نوشت:

$$۲ \theta = \theta + \theta$$

بنابراین، با استفاده از روابط مثلثاتی جمع دو زاویه، روابط مثلثاتی زیر برای سینوس و کسینوس زاویه مضاعف به دست می‌آیند:

$$\sin ( ۲ \theta ) = = \frac { ۲ \tan \theta } { ۱ + \tan ^ ۲ \theta }$$

$$\cos ( ۲ \theta ) = \frac { ۱ - \tan \theta }{ ۱ + \tan ^ ۲ \theta }$$

کسینوس زاویه مضاعف، فرمول‌های دیگری نیز دارد که در ادامه، دو مورد از آن‌ها آورده شده‌اند:

$$\cos ( ۲ \theta ) = ۲ \cos ^ ۲ \theta - ۱$$

$$\cos ( ۲ \theta ) = ۱ - ۲ \sin ^ ۲ \theta$$

مثال ۸: اثبات فرمول های کسینوس زاویه مضاعف

فرمول کسینوس زاویه ۲θ را اثبات کنید.

فرمول کسینوس زاویه ۲θ عبارت است از:

$$\cos ( ۲ \theta ) = \cos ^ ۲ \theta - \sin ^ ۲ \theta$$

برای اثبات این فرمول، زاویه ۲θ را به صورت حاصل جمع دو زاویه θ می‌نویسیم:

$$\cos ( \theta  + \theta ) = \cos ^ ۲ \theta - \sin ^ ۲ \theta$$

بر اساس رابطه کسینوس جمع دو زاویه، داریم:

$$\cos ( \alpha + \beta ) = \cos \alpha \cos \beta − \sin \alpha \sin \beta$$

به جای α و β در این رابطه، θ را قرار می‌دهیم:

$$\cos ( \theta + \theta ) = \cos \theta \cos \theta − \sin \theta \sin \theta$$

$$\cos ( \theta + \theta ) = \cos ^ ۲ \theta− \sin ^ ۲ \theta$$

$$\cos ( ۲ \theta ) = \cos ^ ۲ \theta− \sin ^ ۲ \theta$$

به این ترتیب، فرمول کسینوس زاویه ۲θ اثبات می‌شود.

نسبت های مثلثاتی نصف یک زاویه

اگر یک زاویه را نصف کنیم، نسبت‌های مثلثاتی آن با استفاده از روابط زیر به دست می‌آید:

$$\sin ( \frac { \theta } { ۲ } ) = \pm \sqrt { \frac { ۱ - \cos \theta } { ۲ } }$$

$$\cos ( \frac { \theta } { ۲ } ) = \pm \sqrt { \frac { ۱ + \cos \theta } { ۲ } }$$

$$\tan ( \frac { \theta } { ۲ } ) = \pm \sqrt { \frac { ۱ - \cos \theta } { ۱ + \cos \theta } }$$

$$\cot ( \frac { \theta } { ۲ } ) = \pm \sqrt { \frac { ۱ + \cos \theta } { ۱ - \cos \theta } }$$

برای تانژانت نصف یک زاویه، رابطه دیگری نیز وجود دارد که در ادامه به اثبات آن می‌پردازیم. به این منظور، ابتدا صورت و مخرج کسر زیر رادیکال را در عبارت $$( ۱ - \cos \theta )$$ ضرب می‌کنیم:

$$\tan ( \frac { \theta } { ۲ } ) = \sqrt { \frac { ( ۱ - \cos \theta ) ( ۱ - \cos \theta ) } { ( ۱ + \cos \theta ) ( ۱ - \cos \theta ) }}$$

با ضرب و ساده‌سازی عبارت‌ها، صورت و مخرج کسر به شکل زیر درمی‌آیند:

$$\tan ( \frac { \theta } { ۲ } ) = \sqrt { \frac { ( ۱ - \cos \theta )^ { ۲ } } { ۱ - \cos ^ { ۲ } \theta } }$$

بر اساس رابطه $$\sin ^ ۲ \theta + \cos ^ ۲ \theta = ۱$$، مخرج کسر برابر با $$\sin ^ ۲ \theta$$ است:

$$\tan ( \frac { \theta } { ۲ } ) = \sqrt { \frac { ( ۱ - \cos \theta )^ { ۲ } } { \sin ^ { ۲ } \theta } }$$

اکنون می‌توانیم صورت و مخرج را از زیر رادیکال خارج کنیم:

$$\tan ( \frac { \theta } { ۲ } ) = \frac { ۱ - \cos \theta } { \sin \theta }$$

به این ترتیب، به رابطه دیگری برای تانژانت نصف یک زاویه می‌رسیم.

نسبت های مثلثاتی تبدیل جمع به ضرب و ضرب به جمع

از معروف‌ترین و پرکاربردترین روابط مثلثاتی، می‌توان به فرمول‌های تبدیل جمع به ضرب و ضرب به جمع اشاره کرد.

فرمول‌های تبدیل به جمع به ضرب نسبت های مثلثاتی به صورت زیر نوشته می‌شوند:

$$\begin{aligned} & \sin \alpha + \sin \beta = ۲ \sin \left ( \frac { \alpha + \beta } { ۲ }\right) \cos \left ( \frac { \alpha - \beta } { ۲ } \right) \ & \sin \alpha - \sin \beta = ۲ \sin \left ( \frac { \alpha - \beta } { ۲ }\right) \cos \left ( \frac { \alpha + \beta } { ۲ } \right ) \ & \cos \alpha - \cos \beta = - ۲ \sin \left ( \frac { \alpha + \beta } { ۲ } \right) \sin \left ( \frac { \alpha - B } { ۲ } \right ) \ & \cos \alpha + \cos \beta = ۲ \cos \left ( \frac { \alpha + \beta } { ۲ } \right ) \cos \left ( \frac { \alpha - \beta } { ۲ } \right ) \end{aligned}$$

روابط تبدیل ضرب به جمع نسبت های مثلثاتی نیز عبارت هستند از:

$$\sin A \cos B = \frac { ۱ }{ ۲ } [ \sin ( A + B ) + \sin ( A - B ) ]$$

$$\cos A \sin B = \frac { ۱ }{ ۲ } [ \sin ( A + B ) - \sin ( A - B ) ]$$

$$\cos A \cos B = \frac { ۱ }{ ۲ } [ \cos ( A + B ) + \cos ( A - B ) ]$$

$$\sin A \sin B = \frac { ۱ }{ ۲ } [ \cos ( A - B ) - \cos ( A + B ) ]$$

مثال ۹: محاسبه جمع دو نسبت مثلثاتی

حاصل‌جمع سینوس زاویه ۱۰۵ درجه با سینوس زاویه ۱۵ درجه را به دست بیاورید. (رادیکال ۶ را برابر با ۲/۴۵ در نظر بگیرید.)

برای حل این مثال، می‌توانیم از فرمول زیر استفاده کنیم:

$$\sin \alpha + \sin \beta = ۲ \sin \left ( \frac { \alpha + \beta } { ۲ }\right) \cos \left ( \frac { \alpha - \beta } { ۲ } \right) \$$

به جای α، زاویه ۱۰۵ درجه و به جای β، زاویه ۱۵ درجه را قرار می‌دهیم:

$$\sin ۱۰۵ ^ { \circ } + \sin ۱۵ ^ { \circ } = ۲ \sin \left ( \frac { ۱۰۵ ^ { \circ } + ۱۵ ^ { \circ }} { ۲ }\right) \cos \left ( \frac { ۱۰۵ ^ { \circ } - ۱۵ ^ { \circ } } { ۲ } \right) \$$

$$\sin ۱۰۵ ^ { \circ } + \sin ۱۵ ^ { \circ } = ۲ \sin \left ( \frac { ۱۲۰ ^ { \circ } } { ۲ }\right) \cos \left ( \frac { ۹۰ ^ { \circ } } { ۲ } \right) \$$

$$\sin ۱۰۵ ^ { \circ } + \sin ۱۵ ^ { \circ } = ۲ \sin \left ( ۶۰ ^ { \circ }\right) \cos \left ( ۴۵ ^ { \circ } \right) \$$

سینوس زاویه ۶۰ درجه و کسینوس زاویه ۴۵ درجه به ترتیب برابر هستند با:

$$\sin ۶۰ ^ { \circ } = \frac { \sqrt {۳} }{ ۲ }$$

$$\cos ۴۵ ^ { \circ } = \frac { \sqrt {۲} }{ ۲ }$$

این مقادیر را درون رابطه اصلی قرار می‌دهیم:

$$\sin ۱۰۵ ^ { \circ } + \sin ۱۵ ^ { \circ } = ۲ \times \frac { \sqrt {۳} }{ ۲ } \times \frac { \sqrt {۲} }{ ۲ }$$

$$\sin ۱۰۵ ^ { \circ } + \sin ۱۵ ^ { \circ } = \frac {\sqrt { ۳ } \times \sqrt { ۲ } }{ ۲ }$$

$$\sin ۱۰۵ ^ { \circ } + \sin ۱۵ ^ { \circ } = \frac {\sqrt { ۶ } }{ ۲ }$$

$$\sin ۱۰۵ ^ { \circ } + \sin ۱۵ ^ { \circ } = \frac { ۲/۴۵ }{ ۲ }$$

$$\sin ۱۰۵ ^ { \circ } + \sin ۱۵ ^ { \circ } = ۱/۲۲۵$$

در نتیجه، حاصل‌جمع سینوس زاویه ۱۰۵ درجه با سینوس زاویه ۱۵ درجه، تقریبا برابر با ۱/۲۲۵ است.

نسبت های مثلثاتی توان دار

در بخش‌های قبلی، تعداد زیادی از فرمول‌های نسبت های مثلثاتی را معرفی کردیم. در اغلب این روابط، توان توابع مثلثاتی برابر با ۱ بود.

در این بخش، قصد داریم به معرفی برخی از روابط مرتبط با نسبت‌های مثلثاتی توان‌دار بپردازیم. به این منظور، از روابط سینوس توان‌دار شروع می‌کنیم:

$$\sin ^ ۲ \theta = \frac { ۱ - \cos ۲ \theta }{ ۲ }$$

$$\sin ^ ۳ \theta = \frac { ۳ \sin \theta - \sin ۳ \theta }{ ۴ }$$

$$\sin ^ ۴ \theta = \frac { ۳ - ۴ \cos ۲ \theta + \cos ۴ \theta }{ ۸ }$$

$$\sin ^ ۵ \theta = \frac { ۱۰ \sin \theta - ۵ \sin ۳ \theta + \sin ۵ \theta }{ ۱۶ }$$

روابط کسینوس توان‌دار عبارت هستند از:

$$\sin ^ ۲ \theta = \frac { ۱ + \cos ۲ \theta }{ ۲ }$$

$$\sin ^ ۳ \theta = \frac { ۳ \sin \theta + \sin ۳ \theta }{ ۴ }$$

$$\sin ^ ۴ \theta = \frac { ۳ + ۴ \cos ۲ \theta + \cos ۴ \theta }{ ۸ }$$

$$\sin ^ ۵ \theta = \frac { ۱۰ \sin \theta + ۵ \sin ۳ \theta + \sin ۵ \theta }{ ۱۶ }$$

روابط حاصل‌ضرب سینوس و کسینوس توان‌دار نیز به صورت زیر نوشته می‌شوند:

$$\sin ^ ۲ \theta \cos ^ ۲ \theta = \frac {۱ - \cos ۴ \theta }{ ۸ }$$

$$\sin ^ ۳ \theta \cos ^ ۳ \theta = \frac { ۳ \sin ۲ \theta - \sin ۶ \theta }{ ۳۲ }$$

$$\sin ^ ۴ \theta \cos ^ ۴ \theta = \frac { ۳ - ۴ \cos ۴ \theta + \cos ۸ \theta }{ ۱۲۸ }$$

$$\sin ^ ۵ \theta \cos ^ ۵ \theta = \frac { ۱۰ \sin ۲ \theta - ۵ \sin ۶ \theta + \sin ۱۰ \theta }{ ۵۱۲ }$$

مشتق نسبت های مثلثاتی

به نرخ تغییرات یک تابع نسبت به یک متغیر آن، مشتق می‌گویند. این مفهوم پرکاربرد ریاضی، شیب نمودار در یک نقطه مشخص را نمایش می‌دهد. در مطلب «فرمول های مشتق مهم + سوال با جواب و دانلود PDF»، به معرفی فرمول مشتق بسیاری از توابع پرداخته‌ایم.

جدول زیر، خلاصه‌ای فرمول‌های مشتق نسبت های مثلثاتی اصلی است.

این فرمول‌‌ها، در محاسبه شیب خطوط مماس و قائم بر منحنی، نوشتن معادله خطوط مماس و قائم بر منحنی، محاسبه اکسترمم‌های توابع خاص و غیره کاربرد دارند. مهندسان برق، کامپیوتر، مکانیک و غیره از مشتق نسبت های مثلثاتی در برخی از محاسبات استفاده می‌کنند.

اثبات نسبت های مثلثاتی

بسیاری از نسبت های مثلثاتی، به سادگی و با درک رابطه بین اجزای مثلث‌ها قابل اثبات هستند.

به عنوان مثال، در این بخش، یکی از معروف‌ترین روابط بین نسبت‌های مثلثاتی را با استفاده از دایره‌ای به شعاع واحد اثبات می‌کنیم. این رابطه عبارت است از:

$$\sin ^ ۲ { \theta } + \cos ^ ۲ { \theta } = ۱$$

معادله دایره واحد به صورت زیر نوشته می‌شود:

$$x ^ ۲ + y ^ ۲ = ۱$$

همان‌طور که مشاهده می‌کنید، معادله دایره واحد، شباهت زیادی به رابطه $$\sin ^ ۲ { \theta } + \cos ^ ۲ { \theta } = ۱$$ دارد. اکنون، این دایره را در دستگاه محورهای مختصات دوبعدی در نظر می‌گیریم.

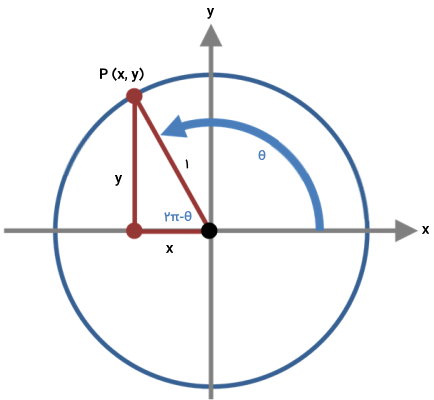
نقطه‌ دلخواه P‌ را بر روی دایره مشخص می‌کنیم. مختصات این نقطه برابر با (x, y) بوده و زاویه خط واصل این نقطه تا مرکز دایره نسبت به محور x برابر با θ است. اگر از نقطه P، خطی را بر محور x عمود کرده و یک خط دیگر را به مرکز دایره وصل کنیم، یک مثلث قائم‌الزاویه به وجود می‌آید. بر اساس فرضیات اثبات، فاصله P تا مرکز دایره یا همان شعاع دایره برابر با ۱ است. زاویه مثلث قائم‌الزاویه در مرکز نیز با حاصل تفریق زاویه ۱۸۰ درجه از θ یا ۲π-θ برابری می‌کند. در ابتدای مقاله دیدیم که سینوس زاویه غیرقائمه در مثلث قائم‌الزاویه از تقسیم طول ضلع مقابل (در اینجا y) بر وتر (در اینجا ۱) به دست می‌آید:

$$\sin { ( ۲ \pi - \theta } ) = \frac { y } { ۱ } = y$$

رابطه کسینوس نیز از تقسیم ضلع مجاور به زاویه مورد نظر (در اینجا x) بر وتر (در اینجا ۱) نوشته می‌شود:

$$\cos { ( ۲ \pi - \theta } ) = \frac { x } { ۱ } = x$$

مطابق با روابط معرفی شده بین نسبت های مثلثاتی، داریم:

$$\sin { ( ۲ \pi - \theta } ) = \sin { \theta }$$

$$\cos { ( ۲ \pi - \theta } ) = \cos { \theta }$$

از مقایسه این دو رابطه با دو رابطه قبلی آن می‌توانیم به روابط زیر برسیم:

$$\sin { \theta } = y$$

$$\cos { \theta } = x$$

اکنون، به جای عبارت‌های x و y در معادله دایره، معادل آن‌ها را قرار می‌دهیم:

$$\cos ^ ۲ { \theta } + \sin ^ ۲ { \theta }= ۱$$

به این ترتیب، اثبات کردیم که جمع مربعات سینوس و کسینوس یک زاویه، همواره برابر با ۱ است. در رابطه با مراحل اثبات دیگر روابط نسبت های مثلثاتی، یک مطلب جامع در مجله فرادرس تهیه شده است که می‌تواند به شما در یادگیری این مبحث کمک کند.

نسبت های مثلثاتی هیپربولیک

توابع هذلولی یا هیپربولیک، مشابه نسبت های مثلثاتی معمولی هستند؛ با این تفاوت که تعریف آن‌ها بر اساس منحنی هذلولی است. سینوس هیپربولیک (sinh)، کسینوس هیپربولیک (cosh)، تانژانت هیپربولیک (tanh)، کتانژانت هیپربولیک (coth)، کسکانت هیپربولیک (csch) و سکانت هیپربولیک (sech)، عنوان شش تابع هذلولی است.

همانطور که مشاهده می‌کنید، نامگذاری این توابع نیز به نامگذاری نسبت‌های مثلثاتی شباهت دارد. تصویر زیر، نمودار توابع هذلولی را نمایش می‌دهد.

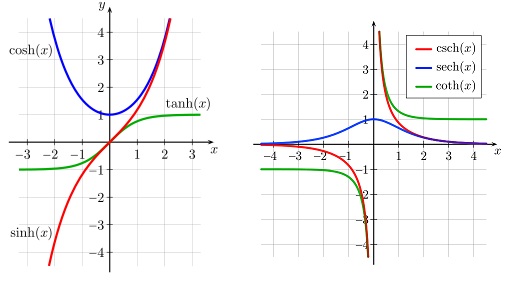
نسبت های مثلثاتی هیپربولیک، بر اساس عدد اویلر تعریف می‌شوند. فرمول‌های ریاضی این نسبت‌ها عبارت هستند از:

$$\sinh x = \frac { e ^ x - e ^ { - x } } { ۲ } = \frac { e ^ { ۲ x } - ۱ } { ۲ e ^ x } = \frac { ۱ - e ^ { - ۲ x } } { ۲ e ^ { - x } }$$

$$\cosh x = \frac { e ^ x + e ^ { - x } } { ۲ } = \frac { e ^ { ۲ x } + ۱ } { ۲ e ^ x } = \frac { ۱ + e ^ { - ۲ x } } { ۲ e ^ { - x } }$$

$$\tanh x = \frac { \sinh x } { \cosh x } = \frac { e ^ { x } - e ^ { - x } } { e ^ { x } + e ^ { - x } } = \frac { e ^ { ۲ x } - ۱ } { e ^ { ۲ x } + ۱ }$$

$$\coth x = \frac { \cosh x } { \sinh x } = \frac { e ^ { x } + e ^ { - x } } { e ^ { x } - e ^ { - x } } = \frac { e ^ { ۲ x } + ۱ } { e ^ { ۲ x } - ۱ }$$

$$\text { csch } { x } = \frac { ۱ } { \sinh x } = \frac { ۲ } { e ^ { x } - e ^ { - x } } = \frac { ۲ e ^ { ۲ x } } { e ^ { ۲ x } - ۱ }$$

$$\text { sech } { x } = \frac { ۱ } { \cosh x } = \frac { ۲ } { e ^ { x } + e ^ { - x } } = \frac { ۲ e ^ { ۲ x } } { e ^ { ۲ x } + ۱ }$$

اگر نسبت‌های مثلثاتی معمولی را بر حسب عدد اویلر بنویسید، شباهت‌های زیادی را بین آن‌ها با نسبت های مثلثاتی هیپربولیک پیدا می‌کنید. مجله فرادرس، در یک مطلب جداگانه به توضیح این شباهت‌ها و دیگر فرمول‌های مرتبط با توابع هذلولی پرداخته است.

کاربرد نسبت های مثلثاتی در زندگی واقعی چیست ؟

هنگام مطالعه مباحث ریاضی و آشنایی با فرمول‌های آن‌ها، احتمالا یکی از سوال‌هایی که در ذهن علم‌آموزان به وجود می‌آید، راجع به کاربرد این مباحث در زندگی واقعی است. مسائل ریاضی، فارغ از کاربردهای قابل لمس، ذهن افراد را برای حل مسائل واقعی تمرین می‌دهند.

بنابراین، در اغلب موارد، هدف از مطالعه ریاضیات، تقویت مهارت حل مسئله، حتی مسائل غیرریاضی است. در مورد نسبت‌های مثلثاتی، این موضوع کمی تفاوت دارد. این نسبت‌ها، در بسیاری از علوم و حتی فعالیت‌های روزمره قابل استفاده هستند. در این بخش، به معرفی برخی از کاربردهای نسبت های مثلثاتی می‌پردازیم.

کاربرد مثلثات در نجوم

از ابتدای شروع تمدن‌های بشری، انسان‌ها به دنبال رسم منظومه شمسی بوده‌اند. منجمان از مثلثات برای محاسبه فاصله بین ستاره‌ها و سیارات دیگر تا زمین استفاده می‌کنند. ساخت و پرتاب سفینه‌های فضایی نیز بر اساس روابط مثلثاتی صورت می‌گیرد. اگر این روابط کشف نمی‌شدند، انسان هرگز نمی‌توانست بر روی ماه قدم بگذارد.

کاربرد مثلثات در موسیقی

مثلثات، یکی از اصول تئوری موسیقی است. امواج صوتی، مطابق با الگوهای تکرارشونده جابجا می‌شوند. تابع سینوس و کسینوس، توابع معرف نحوه گسترش این امواج هستند. یک منحنی سینوسی، می‌تواند معرف یک نُت و ترکیب چندین منحنی سینوسی، می‌توانند معرف یک آکورد باشند. به تصویر کشیدن امواج صوتی در قالب منحنی‌های توابع مثلثاتی، امکان ساخت موسیقی در کامپیوتر و تنظیم صدا به شکل دلخواه را فراهم می‌کند.

کاربرد مثلثات در ساخت و تولید

نسبت‌های مثلثاتی، به طور گسترده در صنعت ساخت مورد استفاده قرار می‌گیرند. مهندسان از این نسبت‌ها برای پیش‌بینی ابعاد و زوایای قطعات مکانیکی به کار رفته در ماشین‌آلات، ابزارآلات و تجهیزات استفاده می‌کنند. این کاربرد، برای صنعت خودروسازی بسیار حیاتی است؛ چراکه امکان اندازه‌گیری دقیق هر آیتم و اطمینان از عملکرد ایمن آیتم‌ها در کنار یکدیگر را فراهم می‌کند. مثلثات، در محاسبه پارچه مورد نیاز برای دوخت لباس با شکل‌های خاص نیز به کار می‌رود.

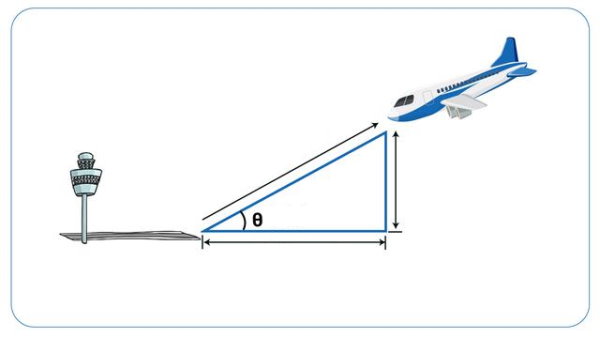
کاربرد مثلثات در مسیریابی

به مطالعه موقعیت اجسام متحرک، مسیریابی می‌گویند. ابزارها و فرمول‌های مختلفی برای انجام مسیریابی و تعیین موقعیت دقیق اجسام متحرک مورد استفاده قرار می‌گیرند. یکی از کاربردهای ملموس نسبت های مثلثاتی در زندگی روزمزه، به کارگیری آن به منظور مسیریابی تعیین فاصله بین دو نقطه است.

کاربرد مثلثات در صنعت پزشکی و داروسازی

در ارتوپدی، از نسبت های مثلثاتی به منظور تعیین زاویه انحراف ستون فقرات و آسیب‌دیدگی احتمالی اعصاب استفاده می‌شود. این نسبت‌ها، در ساخت دست و پای مصنوعی نیز کاربرد دارند. به همین ترتیب، تشخیص و درمان بیماری‌ها توسط روش‌های تصویربرداری، فراصوت، هسته‌ای و مغناطیسی، بر اساس اصول مثلثات انجام می‌گیرند.

سوالات متداول در رابطه با نسبت های مثلثاتی

در این بخش، به برخی از سوالات پرتکرار در رابطه با نسبت‌های مثلثاتی به طور مختص پاسخ می‌دهیم.

نام نسبت های مثلثاتی چیست ؟

سینوس، کسینوس، تانژانت، کتانژانت، کسکانت و سکانت، نام شش نسبت مثلثاتی است.

نسبت های مثلثاتی بیانگر چه هستند ؟

نسبت‌های مثلثاتی، نسبت ضلع‌های یک مثلث قائم‌الزاویه و ارتباط آن با زوایای حاده مثلث را نمایش می‌دهند.

تعریف سینوس در مثلث قائم الزاویه چیست؟

در یک مثلث قائم‌الزاویه، سینوس هر زاویه حاده، برابر با نسبت ضلع مقابل به آن زاویه بر وتر است.

تعریف کسینوس در مثلث مثلث قائم الزاویه چیست؟

در یک مثلث قائم‌الزاویه، کسینوس هر زاویه حاده، برابر با نسبت ضلع مجاور آن زاویه بر وتر است.

تعریف تانژانت در مثلث مثلث قائم الزاویه چیست؟

در یک مثلث قائم‌الزاویه، تانژانت هر زاویه حاده، برابر با نسبت ضلع مقابل به آن زاویه بر ضلع مجاور آن زاویه است.

تعریف کتانژانت در مثلث مثلث قائم الزاویه چیست؟

در یک مثلث قائم‌الزاویه، کتانژانت هر زاویه حاده، برابر با نسبت ضلع مجاور آن زاویه بر ضلع مقابل به آن زاویه است.

تعریف کسکانت در مثلث مثلث قائم الزاویه چیست؟

در یک مثلث قائم‌الزاویه، کسکانت هر زاویه حاده، برابر با نسبت وتر بر ضلع مقابل به آن زاویه است.

تعریف سکانت در مثلث مثلث قائم الزاویه چیست؟

در یک مثلث قائم‌الزاویه، سکانت هر زاویه حاده، برابر با نسبت وتر بر ضلع مجاور آن زاویه است.

رابطه بین تانژانت و کتانژانت چیست ؟

تانژانت و کتانژانت هر زاویه، عکس یکدیگرند. به عبارت دیگر، تانژانت هر زاویه، با تقسیم عدد یک بر کتانژانت آن زاویه برابری می‌کند.

رابطه بین کسکانت و سینوس چیست ؟

سینوس و کسکانت هر زاویه، عکس یکدیگرند. به عبارت دیگر، کسکانت هر زاویه، با تقسیم عدد یک بر سینوس آن زاویه برابری می‌کند.

رابطه بین سکانت و کسینوس چیست ؟

کسینوس و سکانت هر زاویه، عکس یکدیگرند. به عبارت دیگر، سکانت هر زاویه، با تقسیم عدد یک بر کسینوس آن زاویه برابری می‌کند.

علامت کدام یک از نسبت های مثلثاتی در ربع اول دایره واحد مثبت است ؟

علامت تمام نسبت‌های مثلثاتی در ربع اول دایره واحد مثبت است.

علامت کدام یک از نسبت های مثلثاتی در ربع دوم دایره واحد مثبت است ؟

علامت سینوس در ربع دوم دایره واحد مثبت است.

علامت کدام یک از نسبت های مثلثاتی در ربع سوم دایره واحد مثبت است ؟

علامت تانژانت و کتانژانت در ربع سوم دایره واحد مثبت است.

علامت کدام یک از نسبت های مثلثاتی در ربع چهارم دایره واحد مثبت است ؟

علامت کسینوس در ربع چهارم دایره واحد مثبت است.

چگونه علامت نسبت های مثلثاتی را حفظ کنیم ؟

حروف عبارت اختصاری «هستک» (همه، سینوس، تانژانت و کتانژانت، کسینوس)، ابتدای نسبت‌های مثلثاتی دارای علامت مثبت را به ترتیب در ربع‌های اول تا چهارم نمایش می‌دهند.

کدام نسبت های مثلثاتی صفر هستند ؟

سینوس و تانژانت زوایای ۰ و ۱۸۰ درجه به همراه کسینوس و کتانژانت زوایای ۹۰ و ۲۷۰ درجه، برابر با ۰ هستند.

کدام نسبت های مثلثاتی تعریف نشده هستند ؟

تانژانت زوایای ۹۰ و ۲۷۰ درجه به همراه کتانژانت زوایای ۰ و ۱۸۰ درجه تعریف نشده‌اند؛ زیرا عدد ۰ در مخرج این نسبت‌ها ظاهر می‌شود. تقسیم هر عدد بر ۰ نیز یک مقدار تعریف نشده است.