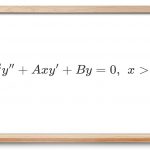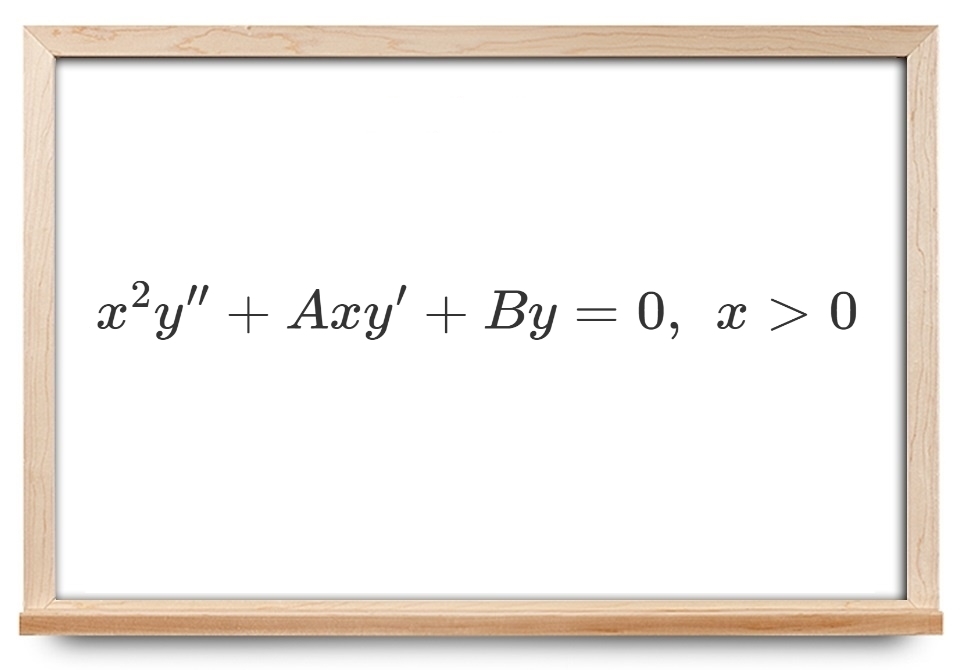معادله اویلر مرتبه دوم – به زبان ساده

در آموزش‌های قبلی مجله فرادرس، با معادلات دیفرانسیل آشنا شدیم. در این آموزش‌ها، روش‌های حل معادلات دیفرانسیل مرتبه اول، معادلات دیفرانسیل مرتبه دوم و معادلات مرتبه بالاتر را معرفی کردیم. همچنین به روش حل معادلات خاص، مانند معادله دیفرانسیل چبیشف پرداختیم. در این آموزش، دسته دیگری از معادلات دیفرانسیل را به نام «معادله اویلر مرتبه دوم» (Second Order Euler Equation) معرفی و روش حل آن‌ را بیان خواهیم کرد.

معادله اویلر مرتبه دوم

معادله دیفرانسیل خطی مرتبه دوم به فرمِ

$$\large { { x ^ 2 } y ^ { \prime \prime } + A x y’ + B y = 0 , \; \; \; } \kern-0.3pt { { x \gt 0 } }$$

یک «معادله دیفرانسیل اویلر مرتبه دوم» (Euler Differential Equation) نامیده می‌شود. این معادله را می‌توان به یک معادله دیفرانسیل همگن خطی با ضرایب ثابت کاهش داد. این کار از دو طریق قابل انجام است که در ادامه آن‌ها را معرفی می‌کنیم.

روش اول حل معادله اویلر مرتبه دوم

از تغییر متغیر $$x = {e^t}$$ استفاده می‌کنیم. بنابراین، مشتقات زیر را خواهیم داشت:

$$\large { y’ = \frac { { d y } } { { d x } } = \frac { { \frac { { d y } } { { d t } } } } { { \frac { { d x } } { { d t } } } } } = { \frac { { \frac { { d y } } { { d t } } } } { { { e ^ t } } } } = { { e ^ { – t } } \frac { { d y } } { { d t } } , }$$

$$\large \begin {align*} y ^ { \prime \prime } & = \frac { d } { { d x } } \left ( { \frac { { d y } } { { d x } } } \right ) = { \frac { d } { { d x } } \left ( { { e ^ { – t } } \frac { { d y } } { { d t } } } \right ) } = { \frac { { \frac { d } { { d t } } } } { { \frac { { d x } } { { d t } } } } \left ( { { e ^ { – t } } \frac { { d y } } { { dt } } } \right) } \\ & = { \frac { { – { e ^ { – t } } \frac { { d y } } { { d t } } + { e ^ { – t } } \frac { { { d ^ 2 } y } } { { d { t ^ 2 } } }} } { { { e ^ t } } } } = { { e ^ { – 2 t } } \left ( { \frac { { { d ^ 2 } y }} { { d { t ^2 } } } – \frac { { d y } } { { d t } } } \right ) . } \end {align*}$$

فیلم آموزش حل معادلات دیفرانسیل با متمتیکا Mathematica در فرادرس

کلیک کنید

با قرار دادن این عبارت در معادله اویلر اصلی، خواهیم داشت:

$$ \large \begin {align*}<br /> \require {cancel} & { { \cancel { e ^ { 2 t } } \cancel { e ^ { – 2 t } } \left ( { \frac { { { d ^ 2 } y } } { { d { t ^ 2 } } } – \frac { { d y } } { { d t } } } \right ) } + { A \cancel { e ^ t } \cancel { e ^ { – t } } \frac { { d y } } { { d t } } + B y = 0 , \; \; } } \\ & \Rightarrow { { \frac { { { d ^ 2 } y } } { { d { t ^ 2 } } } – \frac { { d y } } { {d t } } } + { A \frac { { d y } } { { d t } } + B y = 0 , \; \; } } \Rightarrow { { \frac { { { d ^ 2 } y } } { { d { t ^ 2 } } } + \left ( { A – 1 } \right ) \frac { { d y } } { { d t } } } + { B y = 0 . } }<br /> \end {align*} $$

همان‌طور که می‌بینیم، یک معادله خطی با ضرایب ثابت به دست آمده است. معادله مشخصه مربوط به این معادله دیفرانسیل به صورت زیر است:

$$\large { k ^ 2 } + \left ( { A – 1 } \right ) k + B = 0 .$$

حال می‌توانیم ریشه‌های معادله مشخصه را به دست آورده و جواب عمومی $$y ( t)$$ را بنویسیم. پس از آن، به سادگی به تابع $$y ( x )$$ باز می‌گردیم و داریم:

$$\large y \left ( t \right ) = y \left ( { \ln x } \right ) .$$

روش دوم حل معادله اویلر مرتبه دوم

در روش دوم، باید جواب معادله را به فرم تابع توانی $$y = {x^k}$$ پیدا کنیم که $$k$$ یک عدد مجهول است. در این صورت، خواهیم داشت:

$$\large { \frac { { d y } } { { d x } } = k { x ^ { k – 1 } } , \; \; } \kern-0.3pt { \frac { { { d ^ 2 } y } } { { d { x ^ 2 } } } = k \left ( { k – 1 } \right ) { x ^ { k – 2 } } . }$$

با قرار دادن عبارات بالا در معادله دیفرانسیل، به نتیجه زیر می‌رسیم:

$$\large { { { x ^ 2 } k \left ( { k – 1 } \right ) { x ^ { k – 2 } } } + { A x k { x ^ { k – 1 } } + B { x ^ k } = 0 , \; \; } } \\ \large \Rightarrow { { k \left ( { k – 1 } \right ) { x ^ k } } + { A k { x ^ k } + B { x ^ k } = 0 , \; \; } } \\ \large \Rightarrow { \left [ { k \left ( { k – 1 } \right ) + A k + B } \right ] { x ^ k } } = { 0 . }$$

از آنجا که $${x^k} \ne 0$$، داریم:

$$\large { k \left ( { k – 1 } \right ) + A k + B = 0 , \; \; } \Rightarrow { { k ^ 2 } + \left ( { A – 1 } \right ) k + B = 0 . }$$

این معادله مشخصه، مشابه معادله مشخصه‌ای است که از روش اول به دست آوردیم. پس از یافتن ریشه‌ها می‌توانیم جواب عمومی معادله دیفرانسیل را بنویسیم.

معادله اویلر ناهمگن

معادله اویلر ناهمگن به صورت زیر نوشته می‌شود:

$$\large { { x ^ 2 } \frac { { { d ^ 2 } y } } { { d { x ^ 2 } } } + A x \frac { { d y } } { { d x } } + B y } = { f \left ( x \right ) , \; \; } \kern-0.3pt { { x \gt 0 } . }$$

اگر سمت راست معادله به فرم زیر باشد:

$$\large f \left ( x \right ) = { x ^ \alpha } { P _ m } \left ( { \ln x } \right ) ,$$

می‌توانیم به سادگی جواب عمومی را مشابه روش حل معادلات دیفرانسیل ناهمگن با ضرایب ثابت به دست آوریم. الگوریتم حل به صورت زیر است:

1. جواب عمومی معادله اویلر همگن را محاسبه کنید.
2. با استفاده از روش ضرایب نامعین یا روش تغییر پارامترها، جواب خصوصی وابسته به سمت راست معادله ناهمگن را به دست آورید.
3. جواب عمومی معادله ناهگن، برابر با مجموع جواب عمومی معادله همگن و جواب خصوصی معادله ناهمگن است.

مثال‌ها

در این بخش، چند مثل از حل معادله اویلر مرتبه دوم را بررسی می‌کنیم.

مثال ۱

جواب عمومی معادله دیفرانسیل $$4{x^2}y^{\prime\prime} + y = 0$$ را با فرض $$x > 0$$ به دست آورید.

حل: از تغییر متغیر $$x = e ^ t$$ به صورت زیر استفاده می‌کنیم:

$$\large y ^ { \prime \prime } = { e ^ { – 2 t } } \left ( { \frac { { { d ^ 2 } y } } { { d { t ^ 2 } } } – \frac { { d y } } { { d t } } } \right ) ,$$

بنابراین، معادله به صورت زیر در خواهد آمد:

$$ \large \require {cancel} { { 4 \cancel { e ^ { 2 t } } \cancel { e ^ { – 2t } } \left ( { \frac { { {d ^ 2 } y } } { { d { t ^ 2 } } } – \frac { { d y } } { { d t } } } \right ) } + { y = 0 , \; \; } } \Rightarrow { { 4 \frac { { { d ^ 2 } y } } { { d { t ^ 2 } } } – 4 \frac { { d y } } { { d t } } + y = 0 . } } $$

اکنون ریشه‌های معادله مشخصه متناظر را محاسبه می‌کنیم:

$$\large { 4 { k ^ 2 } – 4 k + 1 = 0 , \; \; } \Rightarrow { D = 1 6 – 1 6 = 0 , \; \; } \Rightarrow { k = \frac { 4 } { { 2 \cdot 4 } } = \frac { 1 } { 2 } . }$$

معادله یک ریشه تکراری دارد و در نتیجه، جواب عمومی $$y ( t)$$ به صورت زیر خواهد بود:

$$\large y \left ( t \right ) = \left ( { { C _ 1 } + { C _ 2 } t } \right ) { e ^ { \large \frac { t } { 2 } \normalsize } } .$$

اکنون می‌توانیم جواب عمومی را به سادگی به فرم $$y ( x )$$ بنویسیم:

$$\large { y \left ( x \right ) } = { \left ( { { C _ 1 } + { C _ 2 } \ln x } \right ) { e ^ { \large \frac { { \ln x } } { 2 } \normalsize } } } = { \left ( { { C _ 1 } + { C _ 2 } \ln x } \right ) { x ^ { \large \frac { 1 } { 2 } \normalsize } } } = { \left ( { { C _ 1 } + { C _ 2 } \ln x } \right ) \sqrt x , }$$

که در آن، $$C _ 1$$ و $$C _ 2$$ اعداد حقیقی دلخواهی هستند.

مثال ۲

معادله دیفرانسیل $${x^2}y^{\prime\prime} – xy’ – 8y = 0$$ را با فرض $$x > 0$$ حل کنید.

حل: از روش دوم، یعنی یافتن جوابی به فرم $$y = {x^k}$$ برای حل معادله استفاده می‌کنیم. بنابراین، داریم:

$$\large { y’ = k { x ^ { k – 1 } } , \; \; } \kern-0.3pt { y ^ { \prime \prime } = k \left ( { k – 1 } \right ) {x ^ { k – 2 } } . }$$

با جایگذاری این عبارات در معادله اصلی، خواهیم داشت:

$$\large \begin {align*} & { { { x ^ 2 } k \left ( { k – 1 } \right ){ x ^ { k – 2 } } } - { x k { x ^ { k – 1 } } – 8 { x ^ k } = 0 , \; \; } } \\ & \Rightarrow { { k \left ( { k – 1 } \right ) { x ^ k } } - { k { x ^ k } – 8 { x ^ k } = 0 , \; \; } } \\\ & \Rightarrow { { \left [ { k \left ( { k – 1 } \right ) – k – 8 } \right ] { x ^ k } } = { 0 . } } \end {align*}$$

معادله مشخصه و ریشه‌های آن نیز به صورت زیر هستند:

$$\large { k \left ( { k – 1 } \right ) – k – 8 = 0 , \; \; } \Rightarrow { { k ^ 2 } – 2 k – 9 = 0 , \; \; } \\ \large \Rightarrow { D = 4 + 3 2 = 3 6 , \; \; } \Rightarrow { { k _ { 1 , 2 } } = \frac { { 2 \pm 6 } } { 2 } = 4 , – 2 . }$$

در نتیجه، جواب عمومی $$y ( t )$$ به صورت زیر خواهد بود:

$$\large y \left ( t \right ) = { C _ 1 } { e ^ { 4 t } } + { C _ 2 } { e ^ { – 2 t } } .$$

تابع $$y ( x )$$ نیز به سادگی برابر خواهد بود با:

$$\large { y \left ( x \right ) } = { { C _ 1 } { e ^ { 4 \ln x } } + { C _ 2 } { e ^ { – 2 \ln x } } } = { { C _ 1 } { x ^ 4 } + { C _ 2 } { x ^ { – 2 } } } = { { C _ 1 } { x ^ 4 } + \frac { { { C _ 2 } } } { { { x ^ 2 } } } . }$$

که در آن، $$C _ 1$$ و $$C _ 2$$ ثابت‌های حقیقی دلخواهی هستند.

مثال ۳

معادله اویلر $${ x ^ 2 } y ^ { \prime \prime } + x y’ + y = 5 { x ^ 2 }$$ را برای $$x > 0$$ حل کنید.

حل: ابتدا جواب عمومی معادله همگن را می‌نویسیم:

$$\large { x ^ 2 } y ^ { \prime \prime } + x y’ + y = 0 .$$

از تغییر متغیر زیر استفاده می‌کنیم:

$$\large { x = { e ^ t } , \; \; } \kern-0.3pt { y’ = { e ^ { – t } } \frac { { d y } } { { d t } } , \; \; } \kern-0.3pt { y ^ { \prime \prime } = { e ^ { – 2 t } } \left ( { \frac { { { d ^ 2 } y } } { { d { t ^ 2 } } } – \frac { { d y } } {{ d t } } } \right ) . }$$

در نتیجه، یک معادله دیفرانسیل به فرم زیر خواهیم داشت:

$$ \large \require {cancel} { { \cancel { e ^ { 2 t } } \cancel { e ^ { – 2 t } } \left ( { \frac { { { d ^ 2 } y } } { { d { t ^ 2 } } } – \frac { { dy } } { { d t } } } \right ) } + { \cancel { e ^ t } \cancel { e ^ { – t } } \frac { { d y } } { { d t } } } + { y = 0 , \; \; } } \\ \large \Rightarrow { { \frac { { { d ^ 2 } y } } { { d { t ^ 2 } } } – \cancel { \frac { { d y } } { { d t } } } + \cancel { \frac { { d y } } { { d t } } } } + { y = 0 , \; \; } } \Rightarrow { \frac { { { d ^ 2 } y } } { { d { t ^ 2 } } } + y = 0 . } $$

معادله مشخصه را حل می‌کنیم:

$$\large {{k^2} + 1 = 0,\;\; }\Rightarrow {{k_{1,2}} = \pm i.}$$

همان‌طور که می‌بینیم، ریشه‌های معادله مشخصه موهومی هستند. بنابراین، جواب عمومی معادله همگن به صورت زیر خواهد بود:

$$\large { { y _ 0 } \left ( t \right ) } = { { C _ 1 } \cos t + { C _ 2 } \sin t , }$$

که در آن، $$C_ 1$$ و $$C_ 2$$ ثابت‌های حقیقی هستند.

اکنون جواب خصوصی معادله ناهمگن را محاسبه می‌کنیم:

$$\large \frac { { { d ^ 2 } y }} {{ d { t ^ 2 } } } + y = 5 { e ^ { 2 t } } .$$

با توجه به عبارت سمت راست معادله اخیر، یک جواب خصوصی به فرم $${y_1}\left( t \right) = a{e^{2t}}$$ خواهیم داشت، که در آن، $$a$$ یک ضریب ثابت است. بنابراین، خواهیم داشت:

$$\large { \frac { { d { y _ 1 } } } { { d t } } = 2 a { e ^ { 2 t } } , \; \; } \kern-0.3pt { \frac { { { d ^ 2 } { y _ 1 } } } {{ d { t ^ 2 } } } = 4 a { e ^ { 2 t } } . }$$

با جایگذاری تابع و مشتقات آن در معادله، ضریب $$a$$ به دست می‌آید:

$$\large { 4 a { e ^ { 2 t } } + a { e ^ { 2 t } } = 5 { e ^ { 2 t } } , \; \; } \Rightarrow { 5 a { e ^ { 2 t } } = 5 { e ^ { 2 t } } , \; \; } \Rightarrow { a = 1 . }$$

بنابراین، یک جواب خصوصی معادله ناهمگن به صورت زیر است:

$$\large { y _ 1 } \left ( t \right ) = { e ^ { 2 t } } .$$

اکنون می‌توانیم جواب عمومی معادله ناهمگن را بنویسیم:

$$\large { y \left ( t \right ) = { y _ 0 } \left ( t \right ) + { y _ 1 } \left ( t \right ) } = { { C _ 1 } \cos t + { C _ 2 } \sin t } + { { e ^ { 2 t } } . }$$

بر حسب متغیر $$x$$ خواهیم داشت:

$$\large { y \left ( x \right ) } = { { C _ 1 } \cos \left ( { \ln x } \right ) } + { { C _ 2 } \sin \left ( { \ln x } \right ) } + { { e ^ { 2 \ln x } } . }$$

از آنجا که $${ e ^ { 2 \ln x } } = { e ^ { \ln { x ^ 2 } } } = x ^ 2$$، جواب نهایی به صورت زیر خواهد بود:

$$\large { y \left ( x \right ) } = { { C _ 1 } \cos \left ( { \ln x } \right ) } + { { C _ 2 } \sin \left ( { \ln x } \right ) } + { { x ^ 2 } . }$$

مثال ۴

معادله اویلر ناهمگن $${ x ^ 2 } y ^ { \prime \prime } – 2 x y’ + 2 y = 6 { x ^ 2 } + 4 \ln x$$ را با فرض $$x > 0$$ حل کنید.

حل: ابتدا معادله همگن را حل می‌کنیم:

$$\large { { x ^ 2 } y ^ { \prime \prime } – 2 x y’ + 2 y } = { 0 . }$$

با قرار دادن $$x = e ^ t$$، می‌توانیم معادله بالا را به معادله‌ای با ضرایب ثابت تبدیل کنیم:

$$\large { \frac { { { d ^ 2 } y } } { { d { t ^ 2 } } } – 3 \frac { { d y } } { { d t } } } + { 2 y } = { 0 . }$$

اکنون ریشه‌های معادله مشخصه را محاسبه کرده و جواب عمومی $$y _ 0 ( t)$$ معادله دیفرانسیل همگن را می‌نویسم:

$$\large { { k ^ 2 } – 3 k + 2 = 0 , \; \; } \Rightarrow { D = 9 – 4 \cdot 2 = 1 , \; \; } \Rightarrow { { k _ { 1 , 2 } } = \frac { { 3 \pm 1 } } { 2 } = 2 , 1 . }$$

بنابراین، خواهیم داشت:

$$\large { { y _ 0 } \left ( t \right ) } = { { C _ 1 } { e ^ { 2 t } } + { C _ 2 } { e ^ t } . }$$

حال، معادله ناهمگن را برحسب $$t$$ می‌نویسیم:

$$\large { { \frac { { { d ^ 2 } y } } { { d { t ^ 2 } } } – 3 \frac { { d y } } { { d t } } + 2 y } = { 6 { e ^ { 2 t } } + 4 \ln \left ( { { e ^ t } } \right ) , \; \; } } \\ \large \Rightarrow { { \frac { { { d ^ 2 } y } }{ { d { t ^ 2 } } } – 3 \frac { { d y } } { { d t } } + 2 y } = { 6 { e ^ { 2 t } } + 4 t . } }$$

ضریب توان $$t$$ تابع نمایی در سمت راست معادله برابر با ۲ است که منطبق با یکی از ریشه‌های معادله مشخصه است. بنابراین، جواب خصوصی به فرم زیر را می‌یابیم:

$$\large { y _ 1 } \left ( t \right ) = a t { e ^ { 2 t } } + b t + c ,$$

که در آن، $$a$$، $$b$$ و $$c$$ اعداد مجهولی هستند.

مشتقات این تابع به صورت زیر هستند:

$$\large { \frac { { d { y _ 1 } } } { { d t } } } = { a {e ^ { 2 t } } + 2 a t { e ^ { 2 t } } + b , }$$

$$\large { \frac { { { d ^ 2 } { y _ 1 } } } { { d { t ^ 2 } } } } = { 2 a { e ^ { 2 t } } + 2 a { e ^ { 2 t } } + 4 a t { e ^ { 2 t } } } = { 4 a { e ^ { 2 t } } + 4 a t { e ^ { 2 t } } . }$$

با قرار دادن این مشتقات در معادله ناهمگن، داریم:

$$ \large \require {cancel} { 4 a { e ^ { 2 t } } + 4 a t { e ^ { 2 t } } }<br /> – { 3 \left ( { a { e ^ { 2 t } } + 2 a t { e ^ { 2 t } } + b } \right ) }<br /> + { 2 \left ( { a t { e ^ { 2 t } } + b t + c } \right ) }<br /> = { 6 { e ^ { 2 t } } + 4 t , } \\ \large { \Rightarrow 4 a { e ^ { 2 t } } + \cancel { 4 a t { e ^ { 2 t } } } – 3a { e ^ { 2 t } } }<br /> – { \cancel { 6 a t { e ^ { 2 t } } } – 3 b }<br /> + { \cancel { 2 a t { e ^ { 2 t } } } + 2 b t + 2 c }<br /> = { 6 { e ^ { 2 t } } + 4 t , } $$

رابطه آخر تحلیلی است، یعنی برای همه مقادیر $$t$$ درست است. با برابر قرار دادن ضرایب جملات مشابه در دو طرف، خواهیم داشت:

$$\large { \left \{ \begin {array} { l } a = 6 \\ 2 b = 4 \\ – 3 b + 2 c = 0 \end {array} \right . , \; \; } \Rightarrow { \left \{ \begin {array} { l } a = 6 \\ b = 2 \\ c = 3 \end {array} \right . . }$$

بنابراین، یک جواب خصوصی معادله ناهمگن به صورت زیر است:

$$\large { { y _ 1 } \left ( t \right ) } = { 6 t { e ^ { 2 t } } + 2 t + 3 . }$$

اکنون می‌توانیم جواب عمومی معادله اویلر ناهمگن را بنویسیم:

$$\large { y \left ( t \right ) = { y _ 0 } \left ( t \right ) + { y _ 1 } \left ( t \right ) } = { { C _ 1 } { e ^ { 2 t } } + { C _ 2 }{ e ^ t } } + { 6 t { e ^ { 2 t } } } + { 2 t + 3 . }$$

از آنجا که $$t = \ln x$$، جواب نهایی به صورت زیر است:‌

$$\large { y \left ( x \right ) } = { { C _ 1 } { x^ 2 } + { C _ 2 } x } + { 6 { x ^ 2 } \ln x } + { 2 \ln x + 3 , }$$

که در آن، $$C _ 1$$ و $$C _ 2$$ ثابت‌های حقیقی هستند.