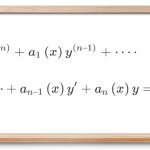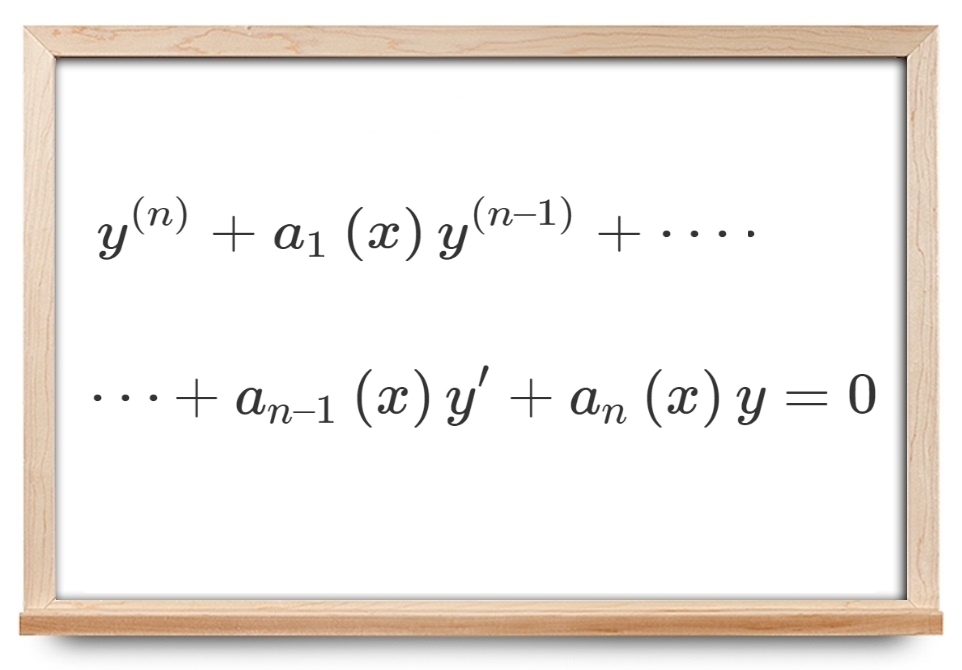معادلات دیفرانسیل مرتبه بالا با ضرایب متغیر – از صفر تا صد

در آموزش‌های قبلی از مجموعه مطالب ریاضیات مجله فرادرس، با معادلات دیفرانسیل آشنا شدیم. در این آموزش‌ها، روش‌های حل معادلات دیفرانسیل مرتبه اول، معادلات دیفرانسیل مرتبه دوم و معادلات مرتبه بالاتر را معرفی کردیم. در این آموزش، نوع خاصی از معادلات دیفرانسیل مرتبه بالا، یعنی معادلات مرتبه بالا با ضرایب متغیر را بررسی می‌کنیم.

معادلات مرتبه بالا با ضرایب متغیر

یک معادله دیفرانسیل مرتبه بالای مرتبه $$n$$ همگن با ضرایب متغیر، به صورت زیر است:

$$\large { { y ^ { \left ( n \right ) } } + { a _ 1 } \left ( x \right ){ y ^ { \left ( { n – 1 } \right ) } } + \cdots } + { { a _ { n – 1 } } \left ( x \right ) y ^ \prime } + { { a _ n } \left ( x \right ) y } = { 0 }$$

که در آن، ضرایب $${a_1}\left( x \right)$$، $${a_2}\left( x \right)$$، $$\cdots$$ و $${a_n}\left( x \right)$$ توابعی پیوسته در بازه $$\left[ {a,b} \right]$$ هستند.

سمت چپ معادله دیفرانسیل را می‌توان با استفاده از عملگر دیفرانسیلی خطی $$L$$ به صورت زیر نوشت:

$$\large L y \left ( x \right ) = 0$$

که در آن، $$L$$ مجموعه‌‌ای از حاصلضرب عملگر‌های دیفرانسیلی و ضرایب $${a_i}\left( x \right)$$ و جمع است.

عملگر $$L$$ خطی است و بنابراین مشخصات زیر را دارد:

1. $$\large L \left [ { { y _ 1 } \left ( x \right ) + { y _ 2 } \left ( x \right ) } \right ] = L \left [ { { y _ 1 } \left ( x \right ) } \right ] + L \left [ { { y _ 2 } \left ( x \right ) } \right ]$$
2. $$\large L \left [ { C y \left ( x \right ) } \right ] = C L \left [ { y \left ( x \right ) } \right ]$$

که در آن، $$y _1 (x)$$ و $$y _2 (x)$$ دلخواه بوده و $$n-1$$ بار مشتق‌پذیر هستند و $$C$$ یک عدد دلخواه است.

با توجه به ویژگی‌های عملگر $$L$$، اگر توابع $$y_1$$، $$y _2$$، $$\ldots$$ و $$y_n$$ جواب‌های معادله دیفرانسیل همگن مرتبه $$n$$ باشند، آنگاه تابعِ

$$\large { y \left ( x \right ) } = { { C _ 1 } { y _ 1 } + { C _ 2 } { y _ 2 } + \cdots } + { { C _ n } { y _ n } }$$

که در آن، $$C_1$$، $$C_2$$، $$\ldots$$ و $$C _n$$ ضرایبی اختیاری هستند، در معادله صدق می‌کند.

اگر توابع $$y_1$$، $$y _2$$، $$\ldots$$ و $$y_n$$ یک دستگاه اساسی از جواب‌ها را تشکیل دهند، عبارت اخیر، جواب عمومی معادله دیفرانسیل همگن خواهد بود.

دستگاه اساسی جواب‌ها

مجموعه $$n$$ جواب خصوصی مستقل خطی $$y _1$$، $$y_2$$، $$\ldots$$ و $$y_n$$، یک دستگاه اساسی معادله دیفرانسیل خطی همگن مرتبه $$n$$ نامیده می‌شوند.

فیلم آموزش معادلات دیفرانسیل با میپل Maple در فرادرس

کلیک کنید

توابع $$y_1$$، $$y _ 2$$، $$\ldots$$ و $$y _n$$ در بازه $$\left[ {a,b} \right]$$ مستقل خطی خواهند بود، اگر تساویِ

$$\large { { \alpha _ 1 } { y _ 1 } + { \alpha _ 2 } { y _ 2 } + \cdots } + { { \alpha _ n } { y _ n } } \equiv { 0 }$$

فقط در شرایط زیر برقرار باشد:

$$\large { { \alpha _ 1 } = { \alpha _ 2 } = \cdots } = { { \alpha _ n } } = { 0 }$$

و در آن، اعداد $${\alpha _1}$$، $${\alpha _2}$$، $$\ldots$$ و $${\alpha _n}$$ همزمان صفر نباشند.

برای آزمایش استقلال خطی توابع، به سادگی می‌توان از رونسکین استفاده کرد:

$$ \large { W \left ( x \right ) = { W _ { { y _ 1 } , { y _ 2 } , \ldots , { y _ n } } } \left ( x \right ) }<br /> = { \left | { \begin {array} { * { 2 0 } { c } }<br /> { { y _ 1 } } & { { y _ 2 } } & \cdots & { { y _ n } } \\<br /> { { y ^ \prime _ 1 } } & { { y ^ \prime _ 2 } } & \cdots & { { y ^ \prime _ n } } \\<br /> \cdots & \cdots & \cdots & \cdots \\<br /> { y _ 1 ^ { \left ( { n – 1 } \right ) } } & { y _ 2 ^ { \left ( { n – 1 } \right ) } } & \cdots & { y _ n ^ { \left ( { n – 1 } \right ) } }<br /> \end {array} } \right | . } $$

فرض کنید توابع $$y _1$$، $$y _2$$، $$\ldots$$ و $$y _n$$، $$n-1$$ بار در بازه $$\left[ {a,b} \right]$$ مشتق‌پذیر باشند. اگر این توابع، در این بازه وابسته خطی باشند، آنگاه تساوی زیر برقرار است:‌

$$\large W \left ( x \right ) \equiv 0 .$$

بر همین اساس، اگر این توابع در بازه مذکور مستقل خطی باشند، عبارت زیر را داریم:

$$\large W \left ( x \right ) \ne 0.$$

دستگاه اساسی جواب‌ها، یک معادله دیفرانسیل همگن خطی را تعریف می‌کند. در عمل، دستگاه اساسی $$y _1$$، $$y_2$$ و $$y _3$$ یک معادله مرتبه سوم را تعریف می‌کند که با دترمینان زیر توصیف می‌شود:

$$ \large { \left | { \begin {array} { * { 2 0 } { c } }<br /> { { y _ 1 } } & { { y _ 2 } } & { { y _ 3 } } & y \\<br /> { { y ’ _ 1 } } & { { y ’ _ 2 } } & { { y ’ _ 3 } } & y ’ \\<br /> { { y ^ { \prime \prime } _ 1 } } & { { y ^ { \prime \prime } _ 2 } } & { { y ^ { \prime \prime } _ 3 } } & y ^ { \prime \prime } \\<br /> { { y ^ { \prime \prime \prime } _ 1 } } & { { y ^ { \prime \prime \prime } _ 2 } } & { { y ^ { \prime \prime \prime } _ 3 } } & y ^ { \prime \prime \prime }<br /> \end {array} } \right | } = { 0 . } $$

به طریق مشابه، توصیف معادله دیفرانسیل مرتبه $$n$$ را می‌توان به صورت زیر نوشت:

$$ \large { \left | { \begin {array} { * { 2 0 } { c } }<br /> { { y _ 1 } } & { { y_ 2 } } & \cdots & { { y _ n } } & y \\<br /> { { y ’ _ 1 } } & { { y ’ _ 2 } } & \cdots & { { y ’ _n } } & y ’ \\<br /> \cdots & \cdots & \cdots & \cdots & \cdots \\<br /> { y _ 1 ^ { \left ( n \right ) } } & { y _ 2 ^ { \left ( n \right ) } } & \cdots & { y _ n ^ { \left ( n \right ) } } & { { y ^ { \left ( n \right ) } } }<br /> \end {array} } \right | } = { 0 . } $$

فرمول لیوویل

فرض کنید توابع $$y _1$$، $$y _2$$،، $$\ldots$$ و $$y _n$$ یک دستگاه اساسی از جواب‌ها برای معادلات دیفرانسیل مرتبه $$n$$ هستند. همچنین فرض کنید نقطه $$x _0$$ در باز ه $$[a , b ]$$ قرار دارد. در این صورت، رونسکین را می‌توان با استفاده از فرمول لیوویل تعیین کرد:

$$\large { W \left ( x \right ) } = { W \left ( { { x _ 0 } } \right ) { e ^ { – \int \limits _ { { x _ 0 } } ^ x { { a _ 1 } \left ( t \right ) d t } } } }$$

که در آن، $${a_1}$$ ضریب مشتق $${y^{\left( {n – 1} \right)}}$$‌ در معادله دیفرانسیل است. در اینجا فرض کرده‌ایم ضریب $${a_0}\left( x \right)$$ مربوط به $${y^{\left( n \right)}}$$ در معادله دیفرانسیل، برابر با $$1$$ باشد. در غیر این صورت، فرمول لیوویل به صورت زیر خواهد بود:

$$\large { W \left ( x \right ) } = { W \left ( { { x _ 0 } } \right ){ e ^ { – \int \limits _ { { x _ 0 } } ^ x { \frac { { { a _ 1 } \left ( t \right ) } } { { { a _ 0 } \left ( t \right ) } } d t } } } , \; \; } \kern-0.3pt { { a _ 0 } \left ( t \right ) \ne 0 , \; \; } \kern-0.3pt { t \in \left [ { a , b } \right ] . }$$

کاهش مرتبه یک معادله خطی همگن

مرتبه معادله همگن خطیِ

$$\large { L y \left ( x \right ) } = { { y ^ { \left ( n \right ) } } + { a _ 1 } \left ( x \right ) { y ^ { \left ( { n – 1 } \right ) } } + \cdots } + { { a _ { n – 1 } } \left ( x \right ) y ’ } + { { a _ n } \left ( x \right ) y } = { 0 }$$

را می‌توان با تغییر متغیر $$y’ = yz$$ کاهش داد. معمولاً‌ تغییر متغیر همیشه منجر به ساده شدن مسئله نمی‌شود، زیرا معادله جدید بر حسب $$z$$ غیرخطی خواهد شد.

اگر جواب خصوصی $$y _ 1$$ را بدانیم، آنگاه مرتبه معادله دیفرانسیل را - ضمن خطی ماندن - می‌توان با تغییر متغیرهای زیر کاهش داد:

$$\large y = { y _ 1 } z , \; \; z ’ = u .$$

در حالت کلی، اگر $$k$$ جواب خصوصی مستقل خطی داشته باشیم، مرتبه معادله را می‌توان به اندازه $$k$$ واحد کاهش داد.

مثال‌ها

در ادامه، چند مثال را از موارد گفته شده بیان می‌کنیم.

مثال ۱

نشان دهید توابع $$x$$، $$\sin x$$ و $$\cos x$$ مستقل خطی هستند.

حل: برای تحقیق استقلال خطی توابع، ماتریس رونسکین $$W (x )$$ آن‌ها را تشکیل می‌دهیم‌:

$$ \large \begin {align*} \require {cancel}<br /> { W \left ( x \right ) } & = { \left | { \begin {array} { * { 2 0 } { c } }<br /> x & { \sin x } & { \cos x } \\<br /> 1& { \cos x } & { – \sin x } \\<br /> 0 & { – \sin x } & { – \cos x }<br /> \end {array} } \right | }<br /> = { x \left | { \begin {array} { * { 2 0 } { c } }<br /> { \cos x } & { – \sin x } \\<br /> { – \sin x } & { – \cos x }<br /> \end {array} } \right | }<br /> – { 1 \cdot \left | { \begin {array} { * { 2 0 } { c } }<br /> { \sin x } & { \cos x } \\<br /> { – \sin x } & { – \cos x }<br /> \end {array} } \right | } \\<br /> & = { x \left ( { – { { \cos } ^ 2 } x – { { \sin } ^ 2 } x } \right ) }<br /> – { 1 \cdot } \kern0pt { \left ( { – \cancel { \sin x \cos x } + \cancel { \sin x \cos x } } \right ) }<br /> = { – x \ne 0 . } \end {align*} $$

فیلم آموزش حل معادلات دیفرانسیل با متمتیکا Mathematica در فرادرس

کلیک کنید

از آنجایی که رونسکین مخالف صفر است، توابع مورد نظر مستقل خطی هستند.

مثال ۲

نشان دهید توابع $$x$$، $$x^ 2$$، $$x ^ 3$$ و $$x ^ 4$$ یک دستگاه مستقل خطی را تشکیل می‌دهند.

حل: رونسکین متناظر با دستگاه توابع را به صورت زیر می‌نویسیم:

$$ \large \begin {align*} { W \left ( x \right ) } & = { \left | { \begin {array} { * { 2 0 } { c } }<br /> x & { { x ^ 2 } } & { { x ^ 3 } } & { { x ^ 4 } } \\<br /> 1 & { 2 x } & { 3 { x ^ 2 } } & { 4 { x ^ 3 } } \\<br /> 0 & 2 & { 6 x} & { 1 2 { x ^ 2 } } \\<br /> 0 & 0 & 6 & { 2 4 x }<br /> \end {array} } \right | \begin {array} { * { 2 0 } { c} }<br /> { } \\<br /> { \small { { R _ 1 } – x { R _ 2 } } \normalsize } \\<br /> { } \\<br /> { }<br /> \end {array} } \\<br /> & = { \left ( { – \frac { 1 } { x } } \right ) \cdot } \kern0pt { \left | { \begin {array} { * { 2 0 } { c } }<br /> x & { { x ^ 2 } } & { { x ^ 3 } } & { { x ^ 4 } } \\<br /> 0 & { – { x ^ 2 } } & { – 2 { x ^ 3 } } & { – 3 { x ^ 4 } } \\<br /> 0 & 2 & { 6 x } & { 1 2 { x ^ 2 } } \\<br /> 0 & 0 & 6 & { 2 4 x }<br /> \end {array}} \right | } \\<br /> & = { { \left ( { – \frac { 1 } { x } } \right ) \cdot x \cdot \left ( { – 1 } \right ) \cdot } \kern0pt { \left | { \begin {array} { * { 2 0 } { c } }<br /> { { x ^ 2 } } & { 2 { x ^ 3 } } & { 3 { x ^ 4 } } \\<br /> 2 & { 6 x } & { 1 2 { x ^ 2 } } \\<br /> 0 & 6 & { 2 4 x }<br /> \end {array} } \right | } } \\<br /> & = { { { x ^ 2 } \left | { \begin {array} { * { 2 0 } { c } }<br /> { 6 x } & { 1 2 { x ^ 2 } } \\<br /> 6 & { 2 4 x }<br /> \end {array} } \right | }<br /> – { 2 \left | { \begin {array} { * { 2 0 } {c } }<br /> { 2 { x ^ 3 }} & { 3 { x ^ 4 } } \\<br /> 6 & { 2 4 x }<br /> \end {array} } \right | } } \\<br /> & = { { x ^ 2 } \left ( { 1 4 4 { x ^ 2 } – 7 2 { x ^ 2 } } \right ) }<br /> – { 2 \left ( { 4 8 { x ^ 4 } – 1 8 { x ^ 4 } } \right ) }<br /> = { 1 2 { x ^ 4 } \ne 0 . } \end {align*} $$

از آنجایی که دترمینان برابر با صفر نیست، این توابع مستقل خطی هستند.

مثال ۳

معادله دیفرانسیلی را بنویسید که بر اساس دستگاه اساسی از توابع $$1$$، $$x ^ 2$$ و $$e ^ x$$ تشکیل شده باشد.

حل: معادله دیفرانسیل را می‌توان بر اساس دترمینان زیر تشکیل داد:

$$ \large { \left | { \begin {array} { * { 2 0 } { c } }<br /> 1 & { { x ^ 2 } } & { { e^ x } } & y \\<br /> 0 & { 2 x } & { { e ^ x } } & { y ’ } \\<br /> 0 & 2 & { { e ^ x } } & { y ^ { \prime \prime } } \\<br /> 0 & 0 & { { e ^ x } } & { y ^ { \prime \prime \prime } }<br /> \end {array} } \right | = 0 , \; \; } \Rightarrow<br /> { 1 \cdot \left | { \begin {array} { * { 2 0 } { c } }<br /> { 2 x } & { { e ^ x } } & { y ’ } \\<br /> 2 & { { e ^ x } } & { y ^ { \prime \prime } } \\<br /> 0 & { { e ^ x } } & { y ^ { \prime \prime \prime } }<br /> \end {array} } \right | = 0 , \; \; } \\ \Rightarrow<br /> { { 2 x \left ( { { e ^ x } y ^ { \prime \prime \prime } – { e ^ x } y ^ { \prime \prime } } \right ) } } - { { 2 \left ( { { e ^ x } y ^ { \prime \prime \prime } – { e ^ x } y ’ } \right ) = 0, \; \; } } \\ \Rightarrow<br /> { { 2 x { e ^ x } y ^ { \prime \prime \prime } – 2 x { e ^ x } y ^ { \prime \prime \prime } } } - { { 2 { e ^ x } y ^ { \prime \prime \prime } + 2 { e ^ x } y ’ = 0 , \; \; }} \\ \Rightarrow<br /> { { 2 { e ^ x } \left ( { x y ^ { \prime \prime \prime } – x y ^ { \prime \prime } } \right . } - { \left . { y ^ { \prime \prime \prime } + y ’ } \right ) = 0 , \; \; } } \\ \Rightarrow<br /> { { \left ( { x – 1 } \right ) y ^ { \prime \prime \prime } } - { x y ^ { \prime \prime } + y ’ = 0 . } } $$

مثال ۴

جواب عمومی معادله دیفرانسیل $$\left ( { 2 x – 3 } \right ) y ^ { \prime \prime \prime } - \; \left ( { 6 x – 7 } \right ) y ^ { \prime \prime } + \; 4 x y ’ – 4 y = 0$$ را با جواب‌های خصوصی $${y_1} = {e^x}$$ و $${y_2} = {e^{2x}}$$ به دست آورید.

حل: از تغییر متغیر $$y = { y _ 1 } z = { e ^ x } z$$ استفاده می‌کنیم. در نتیجه، مشتق‌های اول تا سوم برابرند با:‌

$$\large \begin {align*} y ’ & = { \left ( { { e ^ x } z } \right ) ^ \prime } = { { e ^ x } z + { e ^ x } z ’ } = { { e ^ x } \left ( { z + z ’ } \right ) , } \\ y ^ { \prime \prime } & = { \left [ { { e ^ x } \left ( { z + z ’ } \right ) } \right ] ^ \prime } = { { e ^ x } \left ( { z + z ’ } \right ) + { e ^ x } \left ( { z ’ + z ^ { \prime \prime } } \right ) } \\ & = { { e ^ x } \left ( { z + 2 z ’ + z ^ { \prime \prime } } \right ) , } \\ y ^ { \prime \prime \prime } & = { \left [ { { e ^ x } \left ( { z + 2 z ’ + z ^ { \prime \prime } } \right ) } \right ] ^ \prime } = { { { e ^ x } \left ( { z + 2 z ’ + z ^ { \prime \prime } } \right ) } + { { e ^ x } \left ( { z ’ + 2 z ^ { \prime \prime } + z ^ { \prime \prime \prime } } \right ) } } \\ & = { { { e ^ x } \left ( { z + 3 z ’ + 3 z ^ { \prime \prime } } \right . } + { \left . { z ^ { \prime \prime \prime } } \right ) . } } \end {align*}$$

مشتق مرتبه $$n$$ ضرب دو تابع $$y _1 z$$ را می‌توان به راحتی از فرمول لایب نیتس برای مشتق محاسبه کرد:

$$\large { { y ^ { \left ( n \right ) } } \left ( x \right ) = { \left ( { { y _ 1 } z } \right ) ^ { \left ( n \right ) } } } = { \sum \limits _ { i = 0 } ^ n { \left [ { C _ n ^ i y _ 1 ^ { \left ( i \right ) } { z ^ { \left ( { n – i } \right ) } } } \right ] } . }$$

با جایگذاری مشتق‌ها در معادله و تقسیم آن بر $$e ^ x$$، داریم:

$$\large { { \left ( { 2 x – 3 } \right ) \cdot } \kern0pt { \left ( { z + 3 z ’ + 3 z ^ { \prime \prime } + z ^ { \prime \prime \prime } } \right ) } } \\ \large – { \left ( { 6 x – 7 } \right ) \left ( { z + 2 z ’ + z ^ { \prime \prime } } \right ) } + { 4 x \left ( { z + z ’ } \right ) – 4 z } = { 0 . }$$

بعد از چند عملیات ریاضی ساده، معادله به صورت زیر در خواهد آمد:

$$\large { \left ( { 2 x – 3 } \right)z} + \left( {6x – 9} \right)z’ + \left ( { 6 x – 9 } \right ) z ^ { \prime \prime }$$

$$\large + \left ( { 2 x – 3 } \right ) z ^ { \prime \prime \prime } – { { \left ( { 6 x – 7 } \right ) z } – \left ( { 1 2 x – 1 4 } \right ) z ’ }$$

$$\large – { \left ( { 6 x – 7 } \right ) z ^ { \prime \prime } } + { { 4 x z } + 4 x z ’ – { 4 z } = 0 , \; \; }$$

$$\large \Rightarrow { \left ( { 2 x – 3 } \right ) z ^ { \prime \prime \prime } } - { 2 z ^ { \prime \prime } – \left ( { 2 x – 5 } \right ) z ’ } = { 0 . }$$

با قرار دادن $$z’ = u$$، یک معادله مرتبه دوم خطی همگن به دست می‌آید:

$$\large { \left ( { 2 x – 3 } \right ) u ^ { \prime \prime } – 2 u ’ } - { \left ( { 2 x – 5 } \right ) u } = { 0 . }$$

مرتبه معادله بالا را می‌توان با استفاده از جواب خصوصی دوم، یعنی $${y_2} = {e^{2x}}$$ به یک کاهش داد. تابع $$z _ 2$$ متناظر با این حل است:

$$\large { { y _ 2 } = { y _ 1 } { z _ 2 } , \; \; } \Rightarrow { { z _ 2 } = \frac { { { y _ 2 } } } { { { y _ 1 } } } = \frac { { { e ^ { 2 x } } } } { { { e ^ x } } } = { e ^ x } . }$$

در نتیجه، جواب خصوصی $$u _1$$ به دست می‌آید:

$$\large { { u _ 1 } = { z ’ _ 2 } = { \left ( { { e ^ x } } \right ) ^ \prime } } = { { e ^ x } . }$$

به طریق مشابه داریم:

$$\large { u = { u _ 1 } v = { e ^ x } v , \; \; } \\ \large \Rightarrow { u ’ = { e ^ x } \left ( { v + v ’ } \right ) , \; \; } \\ \large \Rightarrow { u ^ { \prime \prime } = { e ^ x } \left ( { v + 2 v ’ + v ^ { \prime \prime } } \right ) . }$$

معادله دیفرانسیل برای متغیر جدید $$v$$ به صورت زیر خواهد بود:

$$\large { { \left ( { 2 x – 3 } \right ) \left ( { v + 2 v ’ + v ^ { \prime \prime } } \right ) } - { 2 \left ( { v + v ’ } \right ) } - { \left ( { 2 x – 5 } \right ) v = 0 , \; \; } }$$

$$\large \Rightarrow { { \left ( { 2 x – 3 } \right ) v } + \left ( { 4 x – 6 } \right ) v ’ } + \left ( { 2 x – 3 } \right ) v ^ { \prime \prime }$$

$$\large – { 2 v } - { 2 v ’ } - { { \left ( { 2 x – 5 } \right ) v } = 0 , \; \; }$$

$$\large \Rightarrow { \left ( { 2 x – 3 } \right ) v ^ { \prime \prime } + \left ( { 4 x – 8 } \right ) v ’ } = { 0 . }$$

با تعریف $$v’ = w$$ به رابطه زیر می‌رسیم:

$$\large { \left ( { 2 x – 3 } \right ) w ’ } + { \left ( { 4 x – 8 } \right ) w } = { 0 . }$$

معادله اخیر، یک معادله مرتبه اول با متغیرهای جداشدنی است. جواب عمومی این معادله به صورت زیر است:‌

$$\large \begin {align*} \left ( { 2 x – 3 } \right ) \frac { { d w } } { { d x } } = { – \left ( { 4 x – 8 } \right ) w , \; \; } & \Rightarrow { \frac { { d w } } { w } = – \frac { { 4 x – 8 } } { { 2 x – 3 } } d x , \; \; } \\ & \Rightarrow { \int { \frac { { d w } } { w } } = – \int { \frac { { 4 x – 8 } } { { 2 x – 3 } } d x } , \; \; } \\ & \Rightarrow { { \int { \frac { { d w } } { w } } } = { – \int { \left ( { 2 – \frac { 2 } { { 2 x – 3 } } } \right ) d x } , \; \; } } \\ & \Rightarrow { { \ln \left | w \right | } = { – 2 x + \ln \left | { 2 x – 3 } \right | } + { \ln { C _ 1 } , \; \; } } \\ & \Rightarrow { { \ln \left | w \right | = \ln { e ^ { – 2 x } } } + { \ln \left | { 2 x – 3 } \right | } + { \ln { C _ 1 } , \; \; } } \\ & \Rightarrow { { \ln \left | w \right | } = { \ln \left ( { { C _ 1 } \left | { 2 x – 3 } \right | { e ^ { – 2 x } } } \right ) , \; \; } } \\ & \Rightarrow { w = { C _ 1 } \left ( { 2 x – 3 } \right ) { e ^ { – 2 x } } . } \end {align*}$$

اکنون می‌توانیم با انتگرال‌گیری از $$\omega$$ به تابع $$v$$ برسیم:

$$\large { v = \int { w d x } } = { { C _ 1 } \int { \left ( { 2 x – 3 } \right ) { e ^ { – 2 x } } d x } . }$$

حاصل انتگرال به صورت زیر خواهد بود:

$$\large \begin {align*} v & = { C _ 1 } \int { \left ( { 2 x – 3 } \right ) { e ^ { – 2 x } } d x } \\ & = { { { C _ 1 } \left ( { 2 x – 3 } \right ) \left ( { – \frac { 1 } { 2 } } \right ) { e ^ { – 2 x } } } } - { { \int { 2 \left ( { – \frac { 1 } { 2 } } \right ){ e ^ { – 2 x } } d x } } } \\ & = { { { C _ 1 } \left [ { \left ( { – x + \frac { 3 } { 2 } } \right ) { e ^ { – 2 x } } } \right . } +{ \left . { \int { { e ^ { – 2 x } } d x } } \right] }} \\ & = { { { C _ 1 } \left [ { \left ( { – x + \frac { 3 } { 2 } } \right ) { e^ { – 2 x } } } \right . } - { \left . { \frac { 1 } { 2 } {e ^ { – 2 x } } } \right ] } + { { C _ 2 } } } \\ & = { – { C _ 1 } { e ^ { – 2 x } } \left ( {x – \frac { 3 } { 2 } + \frac { 1 } { 2 } } \right ) } + { { C _ 2 } } \\ & = { – { C _ 1 } \left ( { x – 1 } \right ) { e ^ { – 2 x } } } + { { C _ 2 } . } \end {align*}$$

اکنون تابع $$u$$ را محاسبه می‌کنیم:

$$\large \begin {align*} u = { u _ 1 } v = { e ^ x } v & = { { {e ^ x } \left [ { – { C _ 1 } \left ( { x – 1 } \right ) { e ^ { – 2 x } } } \right . } + { \left.{ { C _ 2 } } \right ] } } \\ & = { - { C _ 1 } \left ( { x – 1 } \right ){ e ^ { – x } } } + { { C _ 2 } {e ^ x } . } \end {align*}$$

با یک بار دیگر انتگرال‌گیری، تابع $$z$$ را به دست می‌آوریم:

$$\large \begin {align*} z & = \int { u d x } = { { \int { \left [ { – { C _ 1 } \left ( { x – 1 } \right ) { e ^ { – x } } } \right . } + { \left . { { C _ 2 } { e ^ x } } \right ] d x } } } \\ & = { { – { C _ 1 } \int { \left ( { x – 1 } \right ) { e ^ { – x } } d x } } + { { C _ 2 } \int { { e ^ x } d x } } } \\ & = { { – { C _ 1 } \Big [ { – \left ( { x – 1 } \right ) { e ^ { – x } } } } - { { \int { \left ( { – { e ^ { – x } } } \right ) d x } } \Big ] } } + { { { C _ 2 } \int { { e^ x } d x } } } \\ & = { { – { C _ 1 } \left [ { – \left ( { x – 1 } \right ) { e ^ { – x } } – { e ^ { – x } } } \right ] } + { { C _ 2 } { e ^ x } + { C _ 3 } } } \\ & = { { C _ 1 } x { e ^ { – x } } + { C _ 2 } { e ^ x } + { C _ 3 } . } \end {align*}$$

در نهایت، جواب عمومی $$y (x)$$ را تعیین می‌کنیم:

$$\large \begin {align*} y & = { e ^ x } z = { { e ^ x } \left ( { { C _ 1 } x { e ^ { – x } } + { C _ 2 } { e ^ x } + { C _ 3 } } \right ) } \\ & = { { C _ 1 } x + { C _ 2 } {e ^ { 2 x } } + { C _ 3 } {e ^ x } } \end {align*}$$