مجموع زوایای داخلی چند ضلعی محدب چیست؟ – به زبان ساده + حل مثال

مجموع زوایای داخلی چند ضلعی محدب برابر °۱۸۰ × (n - ۲) است. در این رابطه، n، تعداد ضلع‌های چندضلعی را نمایش می‌دهد. در این آموزش، به معرفی فرمول محاسبه مجموع زوایای داخلی چند ضلعی محدب منتظم و غیر منتظم به همراه حل چندین مثال متنوع و کاربردی می‌پردازیم.

چند ضلعی محدب چیست؟

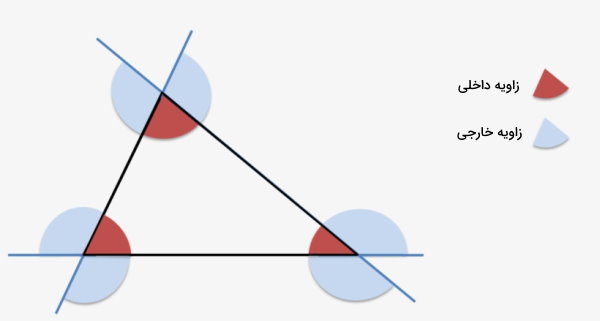
چندضلعی محدب یا کوژ، یک خط شکسته بسته است از راس‌هایی با زاویه کمتر از ۱۸۰ درجه تشکیل می‌شود. تصویر زیر، زوایای داخلی و خارجی یک سه‌ضلعی را نمایش می‌دهد.

در این سه‌ضلعی، تمام زوایای داخلی، کمتر از ۱۸۰ درجه هستند. بنابراین، این شکل، یک چندضلعی محدب در نظر گرفته می‌شود.

مجموع زوایای داخلی چند ضلعی محدب چگونه بدست می آید؟

مجموع زوایای داخلی چند ضلعی محدب، از رابطه زیر به دست می‌‌آید:

۱۸۰° × (۲ - تعداد ضلع‌ها) = مجموع زوایای داخلی

عبارت جبری را بطه بالا به صورت زیر نوشته می‌شود:

$$S = ( n - ۲ ) \times ۱۸۰°$$

این فرمول، برای تعیین جمع زاویه‌های داخلی چندضلعی‌های دیگر نیز مورد استفاده قرار می‌گیرد.

مثال ۱: محاسبه مجموع زوایای داخلی چند ضلعی محدب

در شکل زیر، تمام زاویه‌های داخلی، کوچک‌تر از ۱۸۰ درجه هستند. مجموع این زوایا را حساب کنید.

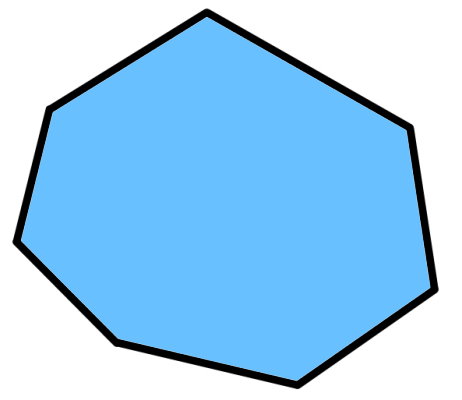
شکل بالا دارای ۷ ضلع بوده و تمام زاویه‌های آن، از ۱۸۰ درجه کمتر هستند. بنابراین، این شکل، یک هفت‌ضلعی محدب در نظر گرفته می‌شود. مجموع زوایای داخلی چندضلعی‌های محدب از فرمول زیر به دست می‌آید:

۱۸۰° × (۲ - تعداد ضلع‌ها) = مجموع زوایای داخلی

۱۸۰° × (۲ -۷) = مجموع زوایای داخلی هفت ضلعی

۱۸۰° × (۵) = مجموع زوایای داخلی هفت ضلعی

۹۰۰° = مجموع زوایای داخلی هفت ضلعی

در نتیجه، مجموع زوایای داخلی شکل، برابر با ۹۰۰ درجه است.

مثال ۲: تعیین نوع چندضلعی محدب

مجموع زوایای داخلی یک چندضلعی محدب برابر با ۱۸۰ درجه است. این چندضلعی چیست؟

به منظور تعیین نوع چندضلعی، فرمول مجموع زوایای داخلی آن را می‌نویسیم:

$$S = ( n - ۲ ) \times ۱۸۰°$$

• S: مجموع زوایای داخلی برابر ۱۸۰ درجه
• n: تعداد ضلع‌ها

اندازه معلوم را درون فرمول قرار می‌دهیم:

$$۱۸۰° = ( n - ۲ ) \times ۱۸۰°$$

$$( n - ۲ ) = \frac { ۱۸۰° } { ۱۸۰° }$$

$$( n - ۲ ) = ۱$$

$$n = ۱ + ۲$$

$$n = ۳$$

تعداد ضلع‌های چندضلعی برابر با ۳ است. چندضلعی محدب با سه ضلع، مثلث نام دارد. مجموع زوایای داخلی مثلث، همواره برابر با ۱۸۰ درجه است.

مثال ۳: محاسبه زاویه چندضلعی محدب

مجموع چهار زاویه داخلی یک پنج‌ضلعی برابر با ۴۳۲ درجه است. اندازه زاویه پنجم این چندضلعی را به دست بیاورید. آیا امکان تعیین مقدار هر یک از زاویه‌های دیگر این چندضلعی وجود دارد؟

مجموع زوایای داخلی پنج‌ضلعی مورد سوال برابر است با:

زاویه پنجم + مجموع چهار زاویه = مجموع زوایای داخلی پنج‌ضلعی

بنابراین، زاویه پنجم، با استفاده از رابطه زیر محاسبه می‌شود:

مجموع چهار زاویه - مجموع زوایای داخلی پنج‌ضلعی = زاویه پنجم

مجموع چهار زاویه را داریم. مجموع زوایای داخلی پنج‌ضلعی را نیز از رابطه زیر تعیین می‌کنیم:

$$S = ( n - ۲ ) \times ۱۸۰°$$

• S: مجموع زوایای داخلی
• n: تعداد ضلع‌ها برابر ۵

$$S = ( ۵ - ۲ ) \times ۱۸۰°$$

$$S = ( ۳ ) \times ۱۸۰°$$

$$S = ۵۴۰°$$

مجموع زوایای داخلی پنج ضلعی برابر با ۵۴۰ درجه است. اکنون می‌توانیم زاویه پنجم پنج‌ضلعی را به دست بیاوریم:

مجموع چهار زاویه - مجموع زوایای داخلی پنج‌ضلعی = زاویه پنجم

۴۳۲° - ۵۴۰° = زاویه پنجم

۱۰۸° = زاویه پنجم

در نتیجه، زاویه پنجم برابر با ۱۰۸ درجه است. امکان تعیین مقدار هر یک از چهار زاویه دیگر وجود ندارد. فقط در صورتی این کار شدنی است که چندضلعی محدب، منتظم باشد.

مجموع زوایای داخلی چند ضلعی محدب منتظم

چندضلعی منتظم، یکی از انواع چندضلعی‌ها با ضلع‌های برابر و زاویه‌های هم‌اندازه است. مجموع زوایای داخلی این نوع چندضلعی عبارت است از:

$$S = ( n - ۲ ) \times ۱۸۰°$$

• S: مجموع زوایای داخلی
• n: تعداد ضلع‌ها

به دلیل برابر بودن اندازه تمام زاویه‌های چندضلعی منتظم، امکان محاسبه اندازه هر زاویه توسط فرمول زیر وجود دارد:

$$\theta = \frac {( n - ۲ ) \times ۱۸۰^{ \circ } } { n }$$

• θ: اندازه هر زاویه چندضلعی منتظم
• n: تعداد ضلع‌ها

به خاطر داشته باشید که تمام چندضلعی‌های منتظم، محدب هستند. به عبارت دیگر، هیچ یک از چندضلعی‌های منتظم نمی‌توانند زاویه داخلی بزرگ‌تر از ۱۸۰ درجه داشته باشند.

مثال ۴: محاسبه مجموع زوایای داخلی چند ضلعی محدب منتظم

شکل زیر، یک چهارضلعی منتظم را نمایش می‌دهد. مجموع زوایای داخلی این چهارضلعی را به دست بیاورید. سپس، اندازه هر یک از زاویه‌ها را حساب کنید. این چهارضلعی، با چه عنوانی شناخته می‌شود؟

مجموع زوایای داخلی چهارضلعی بالا برابر است با:

$$S = ( n - ۲ ) \times ۱۸۰°$$

• S: مجموع زوایای داخلی
• n: تعداد ضلع‌ها برابر ۴

$$S = ( ۴ - ۲ ) \times ۱۸۰°$$

$$S = ( ۲ ) \times ۱۸۰°$$

$$S = ۳۶۰°$$

مجموع زوایای داخلی چند ضلعی محدب منتظم با چهار ضلع، برابر با ۳۶۰ درجه است. به منظور محاسبه هر یک از زاویه‌های داخلی، عدد به دست آمده را بر تعداد راس‌ها تقسیم می‌کنیم:

۹۰° = ۴ ÷ ۳۶۰° = هر زاویه چهارضلعی منتظم

مربع، یک چندضلعی محدب با چهار ضلع هم‌اندازه و چهار زاویه قائمه (۹۰ درجه) است. بنابراین، شکل مورد سوال، یک مربع را نمایش می‌دهد. به دلیل مشخص بودن تمام زاویه‌های مربع، می‌توانیم مجموع زوایای داخلی آن را با استفاده از جمع ساده نیز به دست بیاوریم:

۹۰° + ۹۰° + ۹۰° + ۹۰° = مجموع زوایای داخلی مربع

۳۶۰° = مجموع زوایای داخلی مربع

مثال ۵: محاسبه تمام زوایای چندضلعی منتظم

اندازه هر یک از زاویه‌های چندضلعی منتظم زیر را به دست بیاورید.

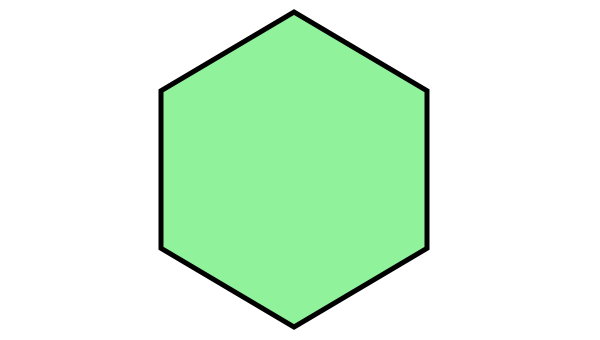
چندضلعی منتظم بالا، دارای شش ضلع است. بنابراین، اندازه هر یک از زاویه‌های داخلی آن از رابطه زیر به دست می‌آید:

$$\theta = \frac {( n - ۲ ) \times ۱۸۰^{ \circ } } { n }$$

• θ: اندازه هر زاویه چندضلعی منتظم
• n: تعداد ضلع‌ها برابر ۶

$$\theta = \frac {( ۶ - ۲ ) \times ۱۸۰^{ \circ } } { ۶ }$$

$$\theta = \frac {( ۴ ) \times ۱۸۰^{ \circ } } { ۶ }$$

$$\theta = \frac {۷۲۰^{ \circ } } { ۶ }$$

$$\theta = ۱۲۰^{ \circ }$$

در نتیجه، هر زاویه داخلی یک شش‌ضلعی منتظم برابر با ۱۲۰ درجه است. توجه داشته باشید که تقریبا در تمام موارد، منظور از زاویه‌های یک چندضلعی، زاویه‌های داخلی آن است. مجموع زوایای خارجی چند ضلعی محدب، نیازی به محاسبه ندارد. در بخش‌های بعدی، به معرفی این زاویه‌ها و ارتباط آن‌ها با زاویه‌های داخلی نیز خواهیم پرداخت.

مثال ۶: محاسبه تعداد ضلع‌های چندضلعی منتظم

زاویه داخلی یکی از راس‌های یک چندضلعی منتظم، برابر با ۱۳۵ درجه است. تعداد ضلع‌های این چندضلعی را حساب کنید.

به منظور محاسبه تعداد ضلع‌های یک چندضلعی منتظم از روی زاویه داخلی آن، ابتدا فرمول زیر را می‌نویسیم و پس از قرار دادن اندازه‌های معلوم، آن را بر حسب n حل می‌کنیم:

$$\theta = \frac {( n - ۲ ) \times ۱۸۰^{ \circ } } { n }$$

• θ: اندازه هر زاویه چندضلعی منتظم برابر ۱۳۵ درجه
• n: تعداد ضلع‌ها

$$۱۳۵^{ \circ } = \frac {( n - ۲ ) \times ۱۸۰^{ \circ } } { n }$$

$$۱۳۵^{ \circ }n = ( n - ۲ ) \times ۱۸۰^{ \circ }$$

$$۱۳۵^{ \circ }n = ۱۸۰^{ \circ }n - ۳۶۰^{ \circ }$$

$$۱۸۰^{ \circ }n - ۱۳۵^{ \circ }n = ۳۶۰^{ \circ }$$

$$۴۵^{ \circ }n = ۳۶۰^{ \circ }$$

$$n = \frac{ ۳۶۰^{ \circ } } { ۴۵^{ \circ } }$$

$$n = ۸$$

در نتیجه، تعداد ضلع‌های چندضلعی برابر با ۸ است. مجموع زوایای داخلی این هشت‌ضلعی منتظم برابر با ۱۰۸۰ درجه خواهد بود.

مجموع زوایای داخلی و خارجی چند ضلعی محدب

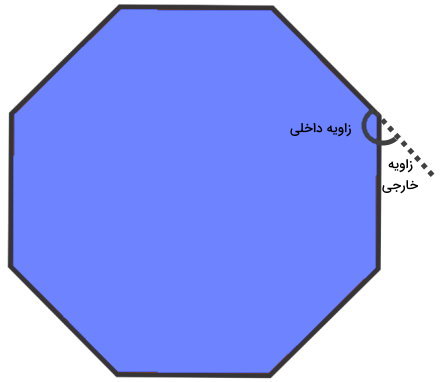
زاویه خارجی چندضلعی محدب، زاویه بین یک ضلع و امتداد ضلع مجاور آن است. زاویه داخلی و خارجی، مکمل یکدیگر هستند:

۱۸۰° = زاویه خارجی + زاویه داخلی

در صورت داشتن زاویه خارجی، امکان تعیین زاویه داخلی مجاور آن فراهم می‌شود.

مثال ۷: تعیین زاویه داخلی ذوزنقه از روی زاویه خارجی

اندازه زاویه A در ذوزنقه زیر را حساب کنید.

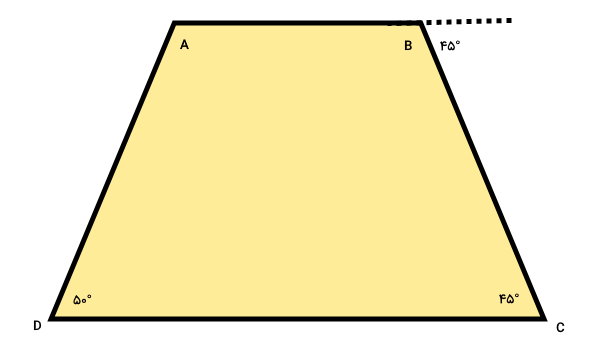
در شکل بالا، دو زاویه داخلی و یک زاویه خارجی ذوزنقه معلوم هستند. به منظور تعیین زاویه A، ابتدا زاویه داخلی B را از روی زاویه خارجی مجاورش به دست می‌آوریم:

۱۸۰° = زاویه خارجی مجاور B + زاویه B

۱۸۰° = ۴۵° + زاویه B

۴۵° - ۱۸۰° = زاویه B

۱۳۵° = زاویه B

زاویه B برابر با ۱۳۵ درجه است. در مرحله بعد، مجموع زوایای داخلی ذوزنقه را محاسبه می‌کنیم:

$$S = ( n - ۲ ) \times ۱۸۰°$$

• S: مجموع زوایای داخلی
• n: تعداد ضلع‌ها برابر ۴

$$S = ( ۴ - ۲ ) \times ۱۸۰°$$

$$S = ( ۲ ) \times ۱۸۰°$$

$$S = ۳۶۰°$$

مجموع زوایای داخلی را به صورت زیر می‌نویسیم:

$$A + B + C + D = ۳۶۰^{ \circ }$$

اندازه زاویه‌های معلوم را درون رابطه بالا جایگذاری می‌کنیم:

$$A + B + C + D = ۳۶۰^{ \circ }$$

$$A + ۲۳۰^{ \circ } = ۳۶۰^{ \circ }$$

$$A = ۳۶۰^{ \circ } - ۲۳۰^{ \circ }$$

$$A = ۱۳۰^{ \circ }$$

به این ترتیب، زاویه A برابر با ۱۳۰ درجه به دست آمد. در این مثال مشاهده کردید که مجموع زوایای داخلی ذوزنقه با مجموع زوایای داخلی مربع برابر شد چراکه مجموع زوایای داخلی چند ضلعی محدب، نَه به شکل، بلکه به تعداد ضلع‌ها بستگی دارد.

اثبات فرمول مجموع زوایای داخلی چند ضلعی محدب

فرمول مجموع زوایای داخلی چند ضلعی محدب، با استفاده از قضیه مجموع زوایای داخلی مثلث اثبات می‌شود.

بر اساس این قضیه، جمع زاویه‌های داخلی هر مثلث، همواره برابر با ۱۸۰ درجه است. با درنظر داشتن این نکته، چند ضلعی محدب زیر را در نظر بگیرید.

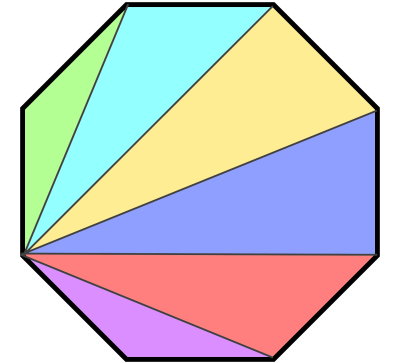
یکی از راس‌های چندضلعی بالا را توسط چند پاره‌خط به تمام راس‌های غیر مجاور وصل کرده‌ایم. با این کار، چندضلعی به چند مثلث تقسیم می‌شود. تعداد این مثلث‌ها، همواره برابر با n-۲ است. n، تعداد ضلع‌های چندضلعی را نمایش می‌دهد. جمع زوایای داخلی چندضلعی، از جمع زوایای داخلی تمام مثلث‌ها به دست می‌آید.

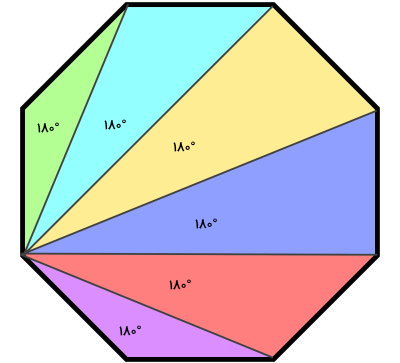
مجموع زوایای داخلی مثلث، همواره برابر با ۱۸۰ درجه است. بنابراین، مجموع زوایای داخلی چندضلعی محدب، از رابطه زیر به دست می‌آید:

۱۸۰° × تعداد مثلث‌ها = مجموع زوایای داخلی

به عبارت دیگر:

۱۸۰° × (۲ - n) = مجموع زوایای داخلی

این رابطه، همان فرمول مجموع زوایای داخلی چند ضلعی محدب است. برای یادگیری نحوه اثبات مجموع زوایای داخلی مثلث، مطالعه مطلب «مجموع زوایای داخلی مثلث چند درجه است؟ + اثبات و مثال به زبان ساده» را به شما پیشنهاد می‌کنیم.