حرکت نسبی چیست؟ – به زبان ساده + فرمول
حرکت نسبی، حرکت بین دو جسم متفاوت است که نسبت به یکدیگر حرکت میکنند. در حرکت نسبی حتی یکی از اجسام میتواند ساکن و جسم دیگر در حال حرکت باشد. حرکت نسبی را میتوانیم از جنبههای مختلفی مانند سرعت، تندی یا شتاب بررسی کنیم. در این مطلب از مجله فرادرس، ابتدا حرکت نسبی را به زبان ساده تعریف، سپس آن را در یک و دو بعد با یکدیگر بررسی و برای درک بهتر آن مثالهای متنوعی را با یکدیگر حل میکنیم.
- یاد میگیرید حرکت نسبی یعنی چه و چارچوب مرجع چه نقشی در آن دارد.
- خواهید توانست سرعت و شتاب نسبی را با استفاده از فرمول تفاضلی محاسبه کنید.
- یاد میگیرید چگونه جهت و علامت سرعت در چارچوبهای مختلف تغییر میکند.
- با روش حل مسائل حرکت نسبی یکبعدی و دوبعدی آشنا میشوید.
- یاد میگیرید چگونه از بردارها برای ترکیب سرعتها و حل مسائل واقعی استفاده کنید.
- میآموزید چگونه نیروهای جانبی مانند باد یا جریان آب بر حرکت نسبی اثر میگذارند.


حرکت نسبی چیست ؟
لغت «نسبی»، کلمهای بسیار عمومی است و برای بسیاری از کمیتهای فیزیکی، غیرفیزیکی، برداری و نردهای استفاده میشود. هر مقایسهای بین کمیتهای مختلف ماهیتی نسبی دارد. به عنوان مثال، فرض کنید قد پدر شما برابر ۱۷۸ سانتیمتر و قد شما برابر ۱۶۰ سانتیمتر است. اگر از شما بپرسیم «پدرتان نسبت به شما چه قدر بلندتر هستید؟»، پاسخ شما برابر ۱۸ سانتیمتر خواهد بود. ۱۸ سانتیمتر چگونه بهدست آمد؟ به سادگی، قد خودتان را از قد پدرتان کم کردید. این روش را میتوان در همه جا استفاده کرد. با استفاده از این روش میتوانیم سرعت یا شتاب نسبی را بهدست آوریم. سرعت نسبی جسم A نسبت به جسم B به صورت زیر نوشته میشود:
به طور مشابه، شتاب نسبی جسم A نسبت به جسم B به صورت زیر نوشته میشود:
توجه به این نکته مهم است که سرعت نسبی جسم A نسبت به جسم B برابر منفی سرعت نسبی جسم B نسبت به A است:
همچنین، شتاب نسبی جسم A نسبت به جسم B برابر منفی شتاب نسبی جسم B نسبت به A است:
برای درک بهتر این موضوع مثالی را با یکدیگر حل میکنیم.

مثال حرکت نسبی در یک بعد
سارا با سرعت یک متر بر ثانیه به سمت راست و پرنیا با سرعت دو متر بر ثانیه به سمت چپ حرکت میکنند. سرعت سارا نسبت به پرنیا چه مقدار است؟
پاسخ
قبل از پاسخ به این مثال، به این نکته توجه داشته باشید که حرکت نسبی ممکن است در یک یا دوبعد رخ دهد. در این مثال، سارا روی خط مستقیم به سمت راست و پرنیا روی همان خط به سمت چپ حرکت میکند. بنابراین، حرکت نسبی در یکبعد را در نظر میگیریم. سرعت سارا برابر یک متر بر ثانیه به سمت راست یا شرق و سرعت پرنیا برابر ۲ متر بر ثانیه به سمت چپ یا غرب است. قبل از حل این مثال باید با مفهوم دیگری به نام چارچوب مرجع آشنا شویم. چارچوب مرجع شبیه حالتی است که شخصی قاب عکسی دارد و تلاش میکند تمام جهان را از طریق آن مشاهده کند. به بیان دیگر، شخص این قاب به عنوان مرجعی برای دیدن جهان از دید خود انتخاب میکند. یکی از لبههای قاب را محور y و لبه دیگر را محور مینامیم. همچنین، محل تقاطع این دو محور را به عنوان مبدأ مختصات انتخاب میکنیم.

چارچوب نشان داده شده در تصویر بالا، چارچوب مرجع دوبعدی است. در این مثال میخواهیم سرعت سارا نسبت به پرنیا را بهدست آوریم. این بدان معنا است که میخواهیم سرعت سارا را از دید پرنیا بدانیم. برای بهدست آوردن سرعت سارا نسبت به پرنیا باید سرعت سارا را از سرعت پرنیا کم کنیم. اگر سرعت سارا را با و سرعت پرنیا را با نشان دهیم، سرعت نسبی سارا نسبت به پرنیا برابر است با:
با قرار دادن مقدارهای سرعت سارا و پرنیا در رابطه فوق داریم:
بنابراین، سرعت نسبی سارا نسبت به پرنیا برابر ۳ متر بر ثانیه بهدست میآید.
مثال ۱
تمرین و آزمون
حرکت نسبی و چارچوب های مرجع لخت
در بخش قبل و به هنگام حل مثال فهمیدیم برای بهدست آوردن سرعت نسبی بین دو جسم متحرک به چارچوبی به نام چارچوب مرجع نیاز داریم. در این بخش رابطه بین حرکت نسبی و چارچوب مرجع را با جزییات بیشتری بررسی میکنیم. حرکت اجسام و بررسی کمی این حرکت در فیزیک از اهمیت ویژهای برخوردار است. اگر عمیق نگاه کنیم به این نکته پی خواهیم برد که هر جسمی حرکت میکند. بنابراین، بررسی حرکت اجسام مختلف ممکن است کاری چالشبرانگیز باشد. هنگامی که میگوییم اتومبیلی با سرعت ۱۰۰ کیلومتر بر ساعت در بزرگراه حرکت میکند، چرخش سطح زمین به دور مرکز آن با سرعت ۱۷۰۰ کیلومتر بر ساعت در استوا را نادیده گرفتهایم. زمین علاوه بر چرخش به دور محور خود با سرعت ۳۰ کیلومتر بر ثانیه نیز به دور خورشید میچرخد.
به طور مشابه، منظومهشمسی با سرعت ۲۰ کیلومتر بر ثانیه به دور مرکز کهکشان میچرخد و کهکشان راه شیری با سرعت ۲۳۰ کیلومتر بر ثانیه در کیهان حرکت میکند. بنابراین، تصور اینکه اتومبیل موردنظر با سرعت بسیار زیاد ۲۳۰ کیلومتر بر ثانیه در اتوبان حرکت میکند دور از انتظار نیست. این بدان معنا است که در زمینهای خاص و از نقطه نظر سرعت مطلق هیچ تفاوتی میان نشستن در هواپیمای در حال پرواز و نشستن روی صندلی در خانه، وجود ندارد. اما به این نکته توجه داشته باشید که در زندگی روزمره متوجه حرکت زمین، خورشید یا کهکشان نمیشویم. از دید ما، زمین ساکن به نظر میرسد. بنابراین، در بیشتر مواقع در فیزیک، حرکت اجسام را به صورت نسبی نسبت به سطح زمین بررسی میکنیم. برای انجام این کار به چارچوبی به نام چارچوب مرجع لخت نیاز داریم. این چارچوب میتواند فرد، مکان یا جسمی دلخواه باشد که در حالت کاملا ساکن فرض میشود.
پس از انتخاب چارچوب مرجع لخت موردنظر، حرکت اجسام دیگر را نسبت به آن بررسی میکنیم. به عنوان مثال، اگر زمین را به عنوان چارچوب مرجع لخت انتخاب کنیم و حرکت آن به دور خود و خورشید را نادیده بگیریم، جمله «اتومبیل با سرعت ۱۰۰ کیلومتر بر ساعت نسبت به زمین حرکت میکند» معنا پیدا میکند. اما اگر داخل اتومبیل باشیم و با سرعت ثابت حرکت کنیم، اینگونه به نظر میرسد که ما حرکت نمیکنیم بلکه اجسام اطرافِ ما با سرعت ۱۰۰ کیلومتر بر ساعت حرکت و از کنار ما عبور میکنند. در این حالت، اتومبیل، چارچوب مرجع لخت میشود و گویی در حالت سکون قرار دارد و تمام اجسام اطراف نسبت به آن حرکت میکنند. شاید کمی عجیب به نظر برسد که فرض کنیم اتومبیل ساکن است. اما به یاد بیاورید که زمین را نیز ساکن در نظر میگیریم. کلمه نسبی را از یاد نبرید.

به طور حتم از خود پرسیدهاید منظور از لخت در چارچوب مرجع لخت چیست. چارچوب مرجع لخت به چارچوب انتخابی گفته میشود که یا ساکن است و یا با سرعت ثابت حرکت میکند. فرض کنید در قطار متحرکی نشستهاید. توپ کوچکی را به سمت بالا پرتاب میکنید و آن را میگیرید. از نگاه فردی که در قطار قرار دارد، توپ مستقیم و روی خط صاف به سمت بالا حرکت و پس از رسیدن به ارتفاعی بیشینه و تغییر جهت، به سمت پایین حرکت میکند. آیا توپ از دید ناظر روی زمین مسیر مشابهی را طی میکند؟ خیر. از دید ناظر روی زمین، توپ روی مسیر سهمی شکل حرکت میکند. دلیل این موضوع آن است که توپ به هنگام ترک دست، سرعتی برابر سرعت حرکت قطار دارد. به بیان دیگر، سرعت توپ علاوه بر مولفه عمودی، مولفه افقی نیز دارد. اما اگر ناظر داخل چارچوب مرجع لختِ قطار باشد، از دید او قطار در حالت سکون قرار دارد و حرکت نمیکند. از دید این ناظر، اجسام اطراف قطار حرکت میکنند. بنابراین توپ، هیچ سرعت افقی ندارد.
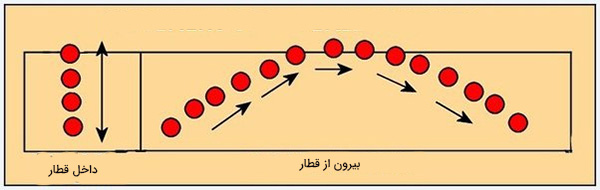
انتخاب چارچوب مرجعِ مناسب و فهمیدن مفهوم آنها بخش مهمی از فیزیک است. گالیله نخستین کسی بود که حرکت نسبی را به طور عمیق مطالعه کرد. او برای مطالعه حرکت نسبی، آزمایشی را در کشتی در حال حرکت انجام داد. گالیله در عرشه کشتی متحرکی با سرعت ثابت ایستاد و توپی را به سمت پایین پرتاب و مسیر حرکت آن را دنبال کرد. توپ بدون انحراف و روی خطی مستقیم به پایین آمد و داخل آب فرو رفت. حرکت توپ در این حالت شبیه حالتی است که کشتی در بندر ساحلی لنگر انداخته و حرکت نمیکند. سپس، گالیله با خود فکر کرد ماهی داخل دریا پرتاب توپ به سمت پایین را چگونه میبیند. از دید ماهی، توپ روی خط مستقیم حرکت نمیکند، بلکه به هنگام پایین آمدن به سمت جلو نیز حرکت خواهد کرد. به بیان دیگر، توپ، نهتنها مولفه عمودی، بلکه مولفه افقی نیز دارد. مسیر حرکت توپ از دید ماهی و گالیله متفاوت است.

گالیله با استفاده از این آزمایش نشان داد اندازهگیری سرعت به چارچوب مرجع انتخابی وابسته است. گالیله با استفاده از این ایده حرکت زمین به دور خورشید را توصیف کرد. این قسمت از کار گالیله، نسبیت گالیله نام گرفت. در حدود دو قرن پس از مطرح شدن نسبیت گالیله، فیزیکدانی به نام اینشتین نظریهای به نام نسبیت خاص را بنا نهاد.
پرتاب سیب
فرض کنید داخل اتومبیلی نشستهاید و به سمت شمال کشور حرکت میکنید. حوصلهتان سر رفته است، برای تفریح سیبی را از پنجره به بیرون پرتاب میکنید. چه چیزی مشاهده میکنید؟ سیب پس از برخورد به زمین به دنبال اتومبیل میآید. چرا؟ هنگامیکه سیب را در دست خود داخل اتومبیل نگه داشتهایم، اینگونه به نظر میرسد که سیب در حالت سکون قرار دارد. اما سیب نسبت به جاده با سرعتی برابر سرعت اتومبیل حرکت میکند. هنگامیکه سیب را از پنجره به بیرون پرت میکنیم، به سیب سرعتی در خلاف جهت سرعت اولیه آن میدهیم. بنابراین، سرعت کلی سیب کاهش مییابد.

سیب هنور به سمت جلو حرکت میکند، اما سرعت آن کمتر از سرعت ماشین است. به همین دلیل، سیب به آهستگی از ماشین دور میشود. سیب حتی پس از برخورد به زمین سرعتی رو به جلو در راستای حرکت اتومبیل دارد. بنابراین، سیب قبل و بعد از برخورد به زمین، سرعت رو به جلو دارد. در نتیجه، پس از برخورد به زمین تا مسافتی به دنبال اتومبیل حرکت میکند. چرا پس از بیرون انداختن سیب از پنجره و قبل از برخورد آن به زمین، حس میکنیم سیب به سمت عقب حرکت میکند؟ دلیل این موضوع به عملکرد مغز بازمیگردد. قبل از برخورد سیب با زمین، مغز حرکت سیب را با توجه به ماشین تجزیه و تحلیل میکند. به بیان دیگر، قبل از برخورد سیب به زمین، مغز، ماشین را به عنوان چارچوب مرجع انتخاب میکند. با توجه به این چارچوب مرجع، سیب سرعتی در خلاف جهت اتومبیل دارد. در واقع، سرعت سیب در این حالت برابر سرعت اولیه موقع پرتاب است. بنابراین، قبل از برخورد سیب به زمین، حرکت آن را به سمت عقب حس میکنیم.
اما پس از برخورد سیب به زمین، مغز حرکت سیب را با توجه به زمین، تجزیه و تحلیل میکند. در این حالت، جهت سرعت سیب به سمت جلو و در راستای حرکت اتومبیل است. در نتیجه، مغز قبل از برخورد سیب به زمین، اتومبیل را به عنوان چارچوب مرجع و پس از برخورد توپ به زمین، زمین را به عنوان چارچوب مرجع انتخاب میکند. این مثال، مقدمهای بر حرکت نسبی و ارتباط آن با انتخاب چارچوب مرجع است.
حرکت نسبی دو قطار نسبت به یکدیگر
فرض کنید داخل کابین قطاری نشستهاید و از پنجره بیرون را تماشا میکنید. در این حال، قطار دیگری را کنار قطار خود مشاهده میکنید. پس از مدتی ملاحظه میکنید که قطار کناری حرکت میکند. از خود میپرسید حرکت قطار به کدام سمت است. پس از مدتی متوجه میشوید که قطار کناری ساکن است و حرکت نمیکند. در واقع، قطار کناری جایی نمیرود، بلکه این قطار شماست که حرکت میکند. گرچه اینگونه به نظر میرسد که قطار کناری در حال حرکت است، این قطار شما است که از ایستگاه دور میشود. عجیب به نظر میرسد. این همان چیزی است که به عنوان حرکت نسبی در فیزیک میشناسیم. حرکت نسبی میگوید مشاهده هر جسمی در حال حرکت این حقیقت را نشان میدهد که ما آن را در حال حرکت میبینیم. اما این بدان معنا نیست که جسم متحرک از دید ما، لزوما نسبت به ناظرهای دیگر نیز حرکت میکند.
شما در قطار نشستهاید و در ابتدا فکر میکنید قطار کناری شروع به حرکت میکند، اما پس از مدتی متوجه میشوید قطار شما در حال دور شدن از ایستگاه است. همچنین، از دید ناظران داخل ایستگاه، قطار شما شروع به حرکت میکند، اما قطار کناری در ایستگاه در حالت سکون قرار دارد و حرکت نمیکند. به این نکته توجه داشته باشید که شما نسبت به قطاری که داخل آن نشستهاید حرکت نمیکنید، اما قطار شما نسبت به مسافران داخل ایستگاه در حال حرکت است. به بیان دیگر، تمام حرکتها به ناظر وابسته است. فرض کنید در ایستگاهِ قطار ایستادهاید و قطاری را مشاهده میکنید که از سمت چپ به سمت راست حرکت میکند. مسافر آکروباتبازی روی سقف قطار ایستاده است. آکروباتباز نیز به همراه قطار از چپ به راست حرکت میکند.

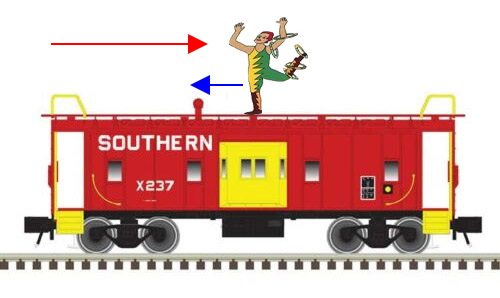
اکنون فرض کنید در قطار نشستهاید. از دید شما قطار حرکت نمیکند. در این لحظه آکروباتباز تصمیم میگیرد روی سقف قطار به سمت جلو و در راستای حرکت قطار راه برود و نمایش اجرا کند. در این حالت، آکروباتباز نسبت به شما که داخل قطار نشستهاید حرکت میکند. سوالی که ممکن است مطرح شود آن است که آکروباتباز با چه سرعتی نسبت به ناظرِ داخل ایستگاه حرکت میکند. آیا او با سرعتی برابر سرعت قطار یا سرعتی بیشتر از آن حرکت میکند؟ اکنون فرض کنید آکروباتباز تصمیم میگیرد در خلاف جهت حرکت قطار و از راست به چپ حرکت کند. از دید شما که در قطار نشستهاید، آکروباتباز به سمت عقب و از راست به چپ حرکت میکند. اما از دید ناظرِ داخل ایستگاه آکروباتباز هنوز در جهت حرکت قطار و از چپ به راست حرکت میکند. چرا؟ زیرا قطار از چپ به راست حرکت میکند.
آکروباتباز در خلاف جهت حرکت قطار حرکت میکند، اما سرعت حرکت او بسیار کمتر از سرعت حرکت قطار است. از اینرو، آکروباتباز از دید ناظرِ داخل ایستگاه از چپ به راست حرکت میکند. به تصویر نشان داده شده در ادامه توجه کنید. سرعت حرکت قطار و آکروباتباز به ترتیب با استفاده از دو پیکان قرمز و آبی نشان داده شدهاند. همانطور که مشاهده میکنید سرعت حرکت قطار بسیار بزرگتر از سرعت حرکت آکروباتباز است.
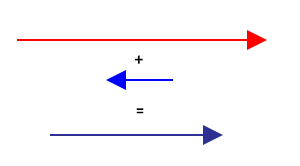
برای بهدست آوردن سرعت حرکت آکروباتباز از دید ناظرِ داخل ایستگاه از جمع برداری استفاده میکنیم. دو بردارِ سرعت در یک راستا، اما در دو جهت مخالف قرار دارند. بنابراین، بردارِ حاصل برابر است با:
در مطالب بالا در مورد چارچوب مرجع صحبت کردیم. چارچوب مرجع و حرکت نسبی، جداناپذیر هستند و با یکدیگر ارتباط نزدیکی دارند. به بیان دیگر، حرکت نسبی به انتخاب چارچوب مرجع بستگی دارد. همانطور که در مطالب بالا اشاره شد چارچوب مرجع همانند قاب عکسی است که از طریق آن جهان را مشاهده میکنیم. چارچوب مرجع دستگاه مختصات دکارتی است که شما در مرکز آن ایستادهاید. هر چیزی که در اطراف خود مشاهده میکنید، نسبت به چارچوب مرجع شما حرکت میکند. اکنون مثال قطار و آکروباتباز را با توجه به چارچوب مرجع بررسی میکنیم. ابتدا حالتی را در نظر میگیریم که روی سکو ایستاده باشد. قطار روی محور از چپ به راست حرکت میکند.
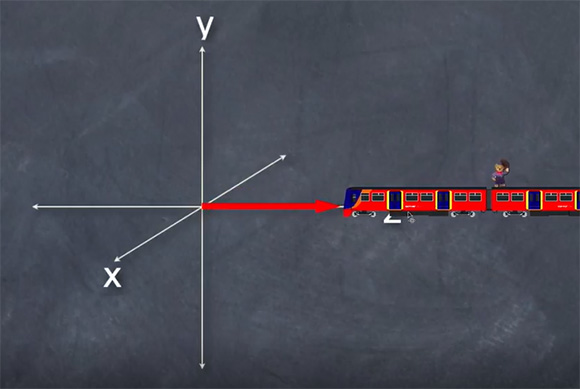
همانطور که در تصویر بالا دیده میشود، حرکت قطار توسط برداری روی محور نشان داده شده است. در ادامه، کمی نزدیکتر نگاه میکنیم و وارد قطار میشویم. در این حالت، چارچوب مرجع با ما سفر میکند. در چارچوب مرجع متصل به قطار، قطار ساکن به نظر میرسد. اما از آنجا که آکروباتباز روی سقف قطار، از چپ به راست، حرکت میکند، نسبت به چارچوب مرجع متصل به قطار، متحرک به نظر میرسد. بردار سرعت آکروباتباز توسط برداری در راستای محور نشان داده شده است.

در این حالت، بردار سرعت آکروباتباز و قطار، همراستا و همجهت هستند. از اینرو، حرکت یا سرعت آکروباتباز نسبت به ناظری ساکن در ایستگاه قطار برابر جمع دو بردار قرمز و قهوهایرنگ است.
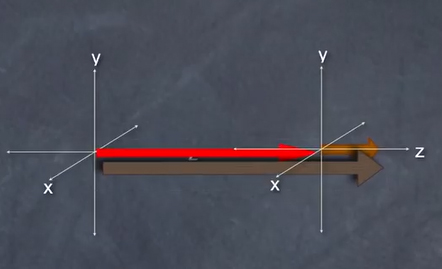
با توجه به تصویر نشان داده شده در بالا، سرعت آکروباتباز نسبت به ناظرِ ساکن در ایستگاه قطار برابر جمع سرعت قطار و سرعت آکروباتباز نسبت به قطار است:
سرعت آکروباتباز نسبت به ناظر ساکن = سرعت قطار + سرعت آکروباتباز نسبت به قطار
اکنون اگر آکروباتبار در خلاف جهت قطار شروع به راه رفتن کند، سرعت آن نسبت به ناظر ساکن روی زمین برابر است با:
سرعت آکروباتباز نسبت به ناظر ساکن = سرعت آکروباتباز نسبت به قطار - سرعت قطار
شاید از خود بپرسید رابطه کلی سرعت نسبی چیست. دو جسم A و B را در نظر بگیرید که نسبت به یکدیگر حرکت میکنند. سرعت جسم A نسبت به ناظر ساکن برابر است با:
رابطه فوق را برحسب مینویسیم:
این رابطه در یک، دو و سه بعد صادق است.
سرعت نسبی
تا اینجا حرکت نسبی را با ذکر مثالهای مختلف توضیح دادیم. نخستین فکری که پس از شنیدن سرعت نسبی به ذهن شما خطور میکند چیست؟ به سرعت جسمی نسبت به جسم دیگر، سرعت نسبی گفته میشود. در بخش قبل کمی در این مورد صحبت کردیم و فرمول کلی سرعت نسبی را نوشتیم. در حالت کلی، به هنگام محاسبه سرعت نسبی، تفاوت میان دو سرعت است. سرعت جسم B نسبت به جسم A است. در اینجا، تمرکز اصلی روی جسم B است و چارچوب مرجع را متصل به جسم A در نظر میگیریم. همانطور که در مطالب بالا اشاره شد، با استفاده از رابطه زیر بهدست میآید:
و به ترتیب سرعتهای دو جسم A و B هستند. سوالی که ممکن است مطرح شود آن است که سرعت این دو جسم نسبت به چه چارچوب مرجعی اندازه گرفته شدهاند. این دو سرعت نسبت به زمین اندازه گرفته میشوند. قطاری با سرعت ۱۲۰ کیلومتر بر ساعت نسبت به زمین حرکت میکند. اگر بدون حرکت روی زمین ایستاده باشیم، سرعت قطار را برابر ۱۲۰ کیلومتر بر ساعت اندازه میگیریم.
مثال سرعت نسبی
شخص A داخل قطار A قرار دارد و این قطار با سرعت ۵۰ کیلومتر بر ساعت نسبت به زمین حرکت میکند. همچنین، شخص B داخل قطار B نشسته است و این قطار با سرعت ۶۰ کیلومتر بر ساعت نسبت به زمین، همجهت با قطار A حرکت میکند. سرعت ناظر A نسبت به ناظر B و ناظر B نسبت به ناظر A را بهدست آورید.
پاسخ
سرعت قطار B ده کیلومتر بر ساعت بزرگتر از قطار A است. سرعت ناظر A نسبت به ناظر B برابر است با:
سرعت ناظر B نسبت به ناظر A برابر است با:
تا اینجا میدانیم حرکت نسبی در حالت کلی چیست. در حرکت نسبی جسمی نسبت به جسم دیگر میتوانیم سرعت یا شتاب نسبی را محاسبه کنیم. در مطالب بالا فهمیدیم چگونه سرعت نسبی را در حالت کلی بهدست آوریم. در ادامه، حرکت نسبی را در یک و دو بعد بررسی میکنیم.
حرکت نسبی در یک بعد
حرکت نسبی در یک بعد را با ذکر مثالی ساده توضیح میدهیم. اتوبانی خارج از شهر را در نظر بگیرید. دو اتومبیل به نامهای A و B در این اتوبان در یک جهت با سرعتهای یکسان ۱۰۰ کیلومتر بر ساعت حرکت میکنند. برای بهدست آوردن سرعت اتومبیل A نسبت به اتومبیل B، سرعت دو اتومبیل را با نشستن در اتومبیل A با یکدیگر مقایسه میکنیم. با مقایسه سرعت دو اتومبیل میبینیم که هر دو با سرعت یکسانی حرکت میکنند. بنابراین، اتومبیل A با سرعت صفر کیلومتر بر ساعت نسبت به اتومبیل B حرکت میکند. اکنون فرض کنید راننده اتومبیل B سرعت آن را به ۱۰۵ کیلومتر بر ساعت افزایش میدهد. سرعت نسبی اتومبیل B نسبت به اتومبیل A چه مقدار است؟ سرعت نسبی اتومبیل B نسبت به A برابر ۵ کیلومتر بر ساعت است. به بیان دیگر، سرعت اتومبیل B پنج کیلومتر بر ساعت بیشتر از اتومبیل A است.
ناظر C بدون حرکت کنار اتوبان ایستاده است. او میبیند اتومبیل A با سرعت ۱۰۰ کیلومتر بر ساعت در اتوبان حرکت میکند. اما ناظر داخل اتومبیل صحنه متفاوتی را میبیند. از دید این ناظر، ناظر C با سرعت ۱۰۰ کیلومتر بر ساعت در خلاف جهت اتومبیل به سمت عقب حرکت میکند. در حرکت نسبی دو جسم نسبت به یکدیگر سه کمیت فیزیکی را بررسی میکنیم:
- جابجایی
- سرعت
- شتاب
برای جابجایی نسبی داریم:
برای سرعت نسبی داریم:
همچنین، شتاب نسبی بین دو جسم نیز به صورت زیر نوشته میشود:
اجازه دهید فرمولهای بالا را با مفهوم بردار بیشتر توضیح دهیم. به این نکته دقت داشته باشید که در این بخش حرکت نسبی در یک بعد را بررسی میکنیم. بنابراین، جسم روی خطی مستقیم به سمت راست یا چپ و بالا یا پایین حرکت میکند. سه اتومبیل A و B و C را فرض کنید که در جادهای مستقیم حرکت میکنند.
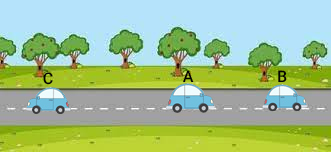
همانطور که در تصویر بالا دیده میشود اتومبیلهای A و B به سمت راست و اتومبیل C به سمت چپ حرکت میکنند. این اتومبیلها را در دستگاه مختصات دوبعدی قرار میدهیم. محل تقاطع دو محور و را به عنوان مبدأ مختصات در نظر میگیریم.
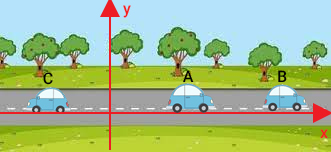
فرض کنید جابجایی اتومبیل A نسبت به مبدأ مختصات برابر ۲ متر و جابجایی اتومبیل B نسبت به مبدأ مختصات برابر ۵ باشد. همچنین، اتومبیل C نسبت به مبدأ مختصات، سه متر جابجا میشود. جابجایی اتومبیل A نسبت به اتومبیل C چه مقدار است؟
$$\overline { x } _ { AC} = \overline { x } _ A - \overline { x } _ C\ $$
با توجه به شکل نشان داده شده در بالا، مثبت و منفی است. بنابراین، جابجایی اتومبیل A نسبت به C برابر است با:
$$\overline { x } _ { AC}= ( 2 ) - (- 3 ) = + \ 5 \ m\ $$
جابجایی اتومبیل C نسبت به اتومبیل A چه مقدار است؟
در ادامه، جابجایی اتومبیل A نسبت به اتومبیل B را بهدست میآوریم:
$$\overline { x } _ { AB} = \overline { x _ A} - \overline { x _ B }\ $$
با قرار دادن مقدارهای نشان داده شده در تصویر بالا را بهدست میآوریم:
بدان معنا است که اتومبیل A را از جایگاه اتومبیل B مشاهده میکنیم. آیا میدانید جابجایی اتومبیل B نسبت به A چه مقدار است؟ از آنجا که جابجایی اتومبیل A نسبت B برابر ۳- متر بهدست آمد، جابجایی اتومبیل B نسبت به A برابر ۳+ متر خواهد بود.
تا اینجا با رابطههای جابجایی، سرعت و شتاب در حرکت نسبی یکبعدی آشنا شدیم. در ادامه، این روابط را اثبات میکنیم.
فرمول های حرکت نسبی در یک بعد
در حرکت نسبی در فضای یکبعدی اجسام و ناظرها روی خطِ مستقیم افقی یا عمودی حرکت میکنند. آنها روی خط مستقیم افقی به سمت چپ یا راست و روی خط مستقیم عمودی، تنها میتوانند به سمت بالا یا پایین حرکت کنند.
جابجایی جسم نقطه ای
دو ناظر A و B را در نظر بگیرید. ناظر A نسبت به زمین ساکن است و ناظر B با سرعت نسبت به ناظر A حرکت میکند. هر دو ناظر حرکت جسمی نقطهای مانند C را تماشا و ناظر B و جسم C در امتداد خط مستقیم یکسانی حرکت میکنند. موقعیت مکانی جسم C نسبت به دو ناظر A و B به ترتیب برابر و است. دو ناظر A و B با چارچوب مرجع متصل به خود در تصویر زیر نشان داده شدهاند.
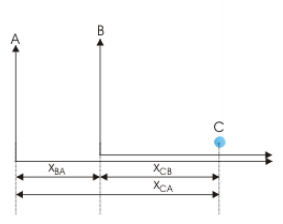
با توجه به تصویر بالا:
سرعت جسم نقطه ای
برای بهدست آوردن سرعت جسم از رابطه نسبت به زمان مشتق میگیریم. از آنجا که اندازهگیریهای انجام شده برای مکان جسم نقطهای در هر یک از چارچوبهای مرجع متفاوت است، انتظار میرود سرعت اندازهگیری شده در هر یک از چارچوبها نیز با یکدیگر تفاوت داشته باشند. دلیل این موضوع آن است یکی از ناظرها ساکن و ناظر دیگر با سرعت ثابت حرکت میکند:
اکنون میتوانیم با استفاده از رابطه ، رابطه بین دو سرعت بالا را بهدست آوریم:
در رابطه فوق:
- سرعت جسم C نسبت به ناظر A است.
- سرعت جسم C نسبت به ناظر B است.
- سرعت ناظر B نسبت به ناظر A است.
مثال اول سرعت نسبی در یک بعد
دو اتومبیل در فاصله مشخصی نسبت به یکدیگر در حالت سکون قرار دارند. سپس هر دو با سرعتهای یک و دو متر بر ثانیه در جادهای مستقیم به سمت یکدیگر شروع به حرکت میکنند. سرعت نزدیک شدن دو اتومبیل به یکدیگر را بهدست آورید.
پاسخ
زمین را با A، ماشین اول را با B و ماشین دوم را با C نشان میدهیم. فرمول سرعت نسبی در این حالت برابر است با:
در اینجا باید جهت مرجعی را برای مشخص کردن علامت سرعتها تعیین کنیم. به این دو نکته توجه داشته باشید که اتومبیلها در خلاف جهت یکدیگر روی خط مستقیم حرکت میکنند، بنابراین علامت سرعت آنها باید مخالف یکدیگر باشد. برای انجام این کار جهت حرکت اتومبیل B را به عنوان جهت مرجع انتخاب میکنیم. جهت مرجع همان جهت مثبت است. در نتیجه:
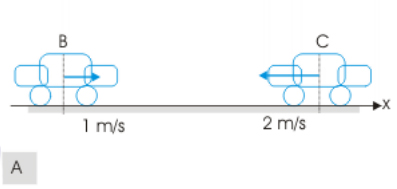
با توجه به انتخاب جهت مرجع یا مثبت، مقدارهای سرعت را در رابطه جایگزین میکنیم:
این بدان معنا است که اتومبیل C در امتداد خط مستقیم با سرعت ۳- متر بر ثانیه به اتومبیل B نزدیک میشود. به طور معادل، اتومبیل B با سرعت ۳ متر بر ثانیه به اتومبیل C در امتداد خط مستقیم نزدیک میشود. بنابراین، دو اتومبیل با سرعت نسبی ۳ متر بر ثانیه به یکدیگر نزدیک میشوند.
شتاب جسم نقطه ای
اگر جسم مشاهده شده با شتاب حرکت کند، شتاب آن با مشتق گرفتن از طرفین رابطه بهدست میآید.
در رابطه فوق:
- شتاب جسم C نسبت به ناظر A است.
- شتاب جسم C نسبت به ناظر B است.
- شتاب ناظر B نسبت به ناظر A است.
به این نکته توجه داشته باشید که در این مطلب چارچوبهای مرجع لخت یا چارچوبهایی که با سرعت ثابت حرکت میکنند را به عنوان چارچوب مرجع انتخاب میکنیم. این بدان معنا است که سرعت نسبی ناظر B نسبت به ناظر A ثابت است. به بیان دیگر، شتاب B نسبت به A برابر صفر است، . بنابراین:
در نتیجه، ناظرهایی که با سرعت ثابت نسبت به یکدیگر حرکت میکنند، شتاب یکسانی را برای جسم نقطهای اندازه میگیرند. این نتیجه یکی از ویژگیهای مهم چارچوبهای مرجع لخت است.
تفسیر معادله سرعت نسبی
نکته مهم در مورد سرعت نسبی در یک بعد آن است که جسم، تنها میتواند در دو جهت چپ و راست یا بالا و پایین حرکت کند. در یک بعد، نیازی به استفاده از بردارها برای بهدست آوردن سرعتهای نسبی نیست. بنابراین، در این حالت میتوانیم با بردار همانند کمیت نردهای یا اسکالر رفتار کنیم. همانطور که در حل مثال حرکت نسبی دیدیم، برای تعیین علامت سرعت، جهتی را به عنوان جهت مرجع یا مثبت انتخاب میکنیم. اگر جسم در جهت مرجع حرکت کند، سرعت آن مثبت و در غیر این صورت، علامت سرعت آن منفی است. معادله سرعت نسبی، رابطه سرعتها نسبت به چارچوبهای مرجع متفاوت را نشان میدهد. معادله سرعتهای نسبی نسبت به چارچوبهای مرجع متفاوت را به صورت زیر بهدست آوردیم:
همانطور که در رابطه فوق دیده میشود، دو سرعت نسبت به A اندازه گرفته شدهاند. A همان چارچوب مرجع زمین است، بنابراین میتوانیم آن را به راحتی حذف کنیم. از اینرو، هر سرعتی با اندیس تکی به معنای سنجیدن آن نسبت به زمین است:
رابطه نوشته شده در بالا، رابطه بسیار مهمی است. این رابطه در حرکت نسبی در یک بعد استفاده میشود. از این معادله برای تعیین سرعت نسبی دو جسم متحرک با سرعتهای یکنواخت (B و C) و با دانستن سرعت آنها نسبت به زمین استفاده میکنیم.
مثال دوم سرعت نسبی در یک بعد
دو اتومبیل در ابتدا در فاصله ۱۰۰ متری از یکدیگر قرار گرفتهاند. سپس با سرعتهای یک و دو متر بر ثانیه در امتداد جاده مستقیم شروع به حرکت به سمت یکدیگر میکنند. زمان رسیدن دو اتومبیل به یکدیگر را بهدست آورید.
پاسخ
سرعت نسبی دو اتومبیل نسبت به یکدیگر (اتومبیلهای ۱ و ۲) برابر است با:
در اینجا جهت را به عنوان جهت مرجع یا جهت مثبت در نظر میگیریم. بنابراین، مقدار برابر ۱+ متر بر ثانیه و مقدار برابر ۲- متر بر ثانیه است. در نتیجه، سرعت نسبی دو اتومبیل نسبت به یکدیگر برابر است با:
این بدان معنا است که اتومبیل ۲ در امتداد جاده مستقیم با سرعت ۳- متر بر ثانیه به اتومبیل یک نزدیک میشود. به طور مشابه، اتومبیل یک در امتداد خط مستقیم با سرعت ۳ متر بر ثانیه به اتومبیل ۲ نزدیک خواهد شد. بنابراین، دو اتومبیل با سرعت ۳ متر بر ثانیه به یکدیگر نزدیک میشوند. فرض کنید دو اتومبیل در مدت زمان t به یکدیگر میرسند.
ترتیب اندیس ها
شاید به هنگام محاسبه کمیتهای نسبی مانند سرعت در حرکت نسبی و به خصوص ترتیب نوشتن اندیسها دچار اشتباه شده باشید. اندیس AB در به معنای سرعت نسبی A نسبت به B است و برای محاسبه آن سرعت B را از سرعت A کم میکنیم.
همچنین، اندیس BA در به معنای سرعت B نسبت به A است و برای محاسبه آن سرعت A را از سرعت B کم میکنیم.
ارزیابی سرعت نسبی با ثابت نگه داشتن جسم مرجع
با بررسی معادله سرعت نسبی به ویژگی جالبی از آن پی میبریم. باید بر این نکته تایید کنیم که معادله سرعت نسبی، معادلهای برداری است. در حرکت یکبعدی، این معادله را میتوانیم به صورت معادلهای بین کمیتهای نردهای بنویسیم.
معادله فوق از دو کمیت برداری و تشکیل شده است. بنابراین سرعت نسبی را میتوانیم به صورت زیر بهدست آوریم:
- سرعت جسم مرجع را (به عنوان مثال جسم A) را برای دو جسم به کار ببرید و جسم مرجع را ساکن در نظر بگیرید.
- سرعت بهدست آمده برای جسم دیگر (B) برابر سرعت نسبی B نسبت به A است.
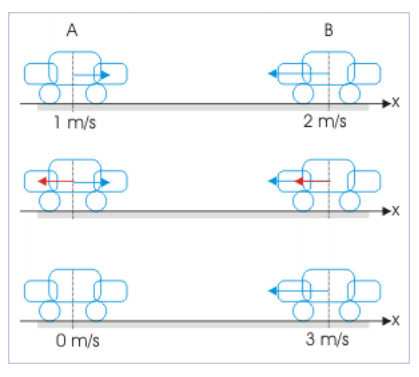
ساکن کردن جسم مرجع در تصویر زیر توضیح داده شده است. برای بهدست آوردن سرعت نسبی اتومبیل B نسبت به اتومبیل A، بردار سرعت اتومبیل A را برای هر دو اتومبیل به کار میبریم. سرعت نسبی اتومبیل B نسبت به اتومبیل A برابر سرعت بهدست آمده اتومبیل B است. این تکنیک، روشی بسیار مناسب برای حرکت نسبی در دو بعد است. در تصویر زیر دو اتومبیل A و B به ترتیب با سرعتهای یک و دو متر بر ثانیه در جادهای مستقیم به سمت یکدیگر حرکت میکنند. اتومبیل A را به عنوان جسم مرجع انتخاب میکنیم و سرعت آن را برابر صفر قرار میدهیم. برای صفر شدن سرعت A باید برداری به اندازه یک و در خلاف جهت (بردار قرمزرنگ) بر آن اعمال کنیم. به طور مشابه، این بردار را بر اتومبیل B نیز اعمال میکنیم. در این حالت، سرعت اتومبیل A برابر صفر و سرعت B برابر ۳ متر بر ثانیه در جهت منفی میشود.
نمودارها در حرکت نسبی در یک بعد
سرعت نسبی ممکن است در مقدار و علامت تغییر کند. با توجه به مقدارهای مطلق اجسام، سرعت نسبی ممکن است مثبت، منفی یا حتی صفر شود. اگر سرعتهای و در یک جهت باشند، سرعت نسبی جسم ۲ نسبت به جسم یک برابر است. اگر دو جسم در دو جهت مخالف حرکت کنند، سرعت نسبی برابر خواهد بود. در ادامه سه حالت مختلفِ حرکت نسبی دو جسم P و Q را بررسی میکنیم.
حالت ۱
در این حالت، دو جسم P و Q در یک جهت و با سرعت یکسانی حرکت میکنند.
هنگامیکه دو جسم با سرعت یکسان در یک جهت حرکت میکنند، فاصله بین آنها همواره ثابت باقی میماند:
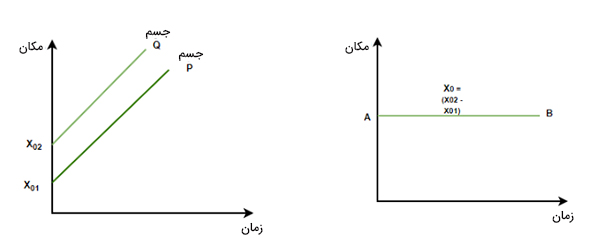
حالت ۲
در این حالت، دو جسم در یک جهت حرکت میکنند و سرعت جسم Q بزرگتر از سرعت جسم P است.
فرض کنید جسم Q جلوتر از جسم P حرکت میکند. هنگامیکه جسم دوم (جسم Q) با سرعت بزرگتری نسبت به جسم اول (P) حرکت میکند، فاصله بین آنها همواره مثبت خواهد بود، زیرا P نمیتواند از Q عبور کند.
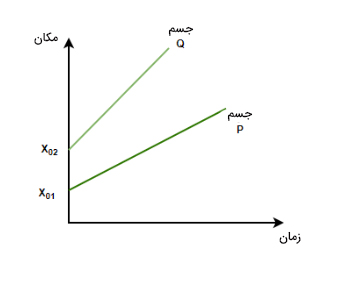
حالت ۳
در این حالت، جسم P با سرعت بزرگتری نسبت به جسم Q در یک جهت حرکت میکنند. بنابراین، جسم P به راحتی از Q میگذرد و تفاوت فاصله بین آنها منفی میشود.
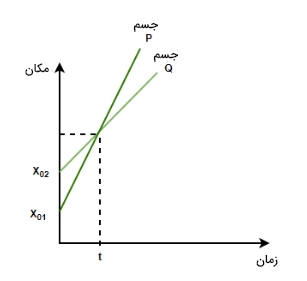
معادلات حرکت در حرکت نسبی
دو ذره یک و دو داریم. معادله مستقل از مکان ذره یک به صورت زیر نوشته میشود:
معادله مستقل از مکان ذره دو نیز به صورت زیر نوشته میشود:
دو معادله فوق را از یکدیگر کم میکنیم.
همانطور که در مطالب بالا گفتیم، برابر سرعت نسبی ذره ۲ نسبت به ذره یک است. همچنین، و نیز به ترتیب سرعت نسبی و شتاب نسبی ذره ۲ نسبت به ذره یک هستند. بنابراین، تفاضل دو رابطه بالا به صورت زیر نوشته میشود:
بنابراین، در حرکت نسبی صورت معادله حرکت مستقل از مکان تغییر نمیکند، اما ماهیت آن نسبی میشود. دیگر معادلات حرکت نیز به صورت مشابه بهدست میآیند.
مثال سوم سرعت نسبی در یک بعد
فردی در مدت زمان از پلهبرقی ساکنی بالا میرود. اگر پلهبرقی روشن باشد و فرد روی یکی از پلهها ساکن باشد در مدت زمان به بالای پلهبرقی میرسد. اگر طول پلهبرقی برابر L باشد:
- تندی فرد نسبت به پلهبرقی را بهدست آورید.
- تندی پله برقی را محاسبه کنید.
- چه مدت زمانی طول میکشد تا فرد از پله برقی روشن بالا برود؟

پاسخ
ابتدا سرعت فرد نسبت به پلهبرقی را بهدست میآوریم. فرد در مدت زمان از پلهبرقی ساکن بالا میرود. برای حل این مثال، فرد را با M و پلهبرقی را با E نشان میدهیم. سرعت نسبی فرد نسبت به زمین به صورت زیر نوشته میشود:
در رابطه فوق:
- سرعت فرد نسبت به پلهبرقی است.
- سرعت پلهبرقی نسبت به زمین است.
اگر پلهبرقی ساکن باشد، سرعت پلهبرقی نسبت به زمین یا برابر صفر خواهد بود. در این حالت، سرعت فرد نسبت به زمین برابر سرعت فرد نسبت به پلهبرقی است. در حالت اول فرد از پلهبرقی ساکن بالا میرود و مسافت L را در مدت زمان طی میکند. بنابراین، سرعت فرد نسبت به زمین برابر است با:
از آنجا که پلهبرقی ساکن و سرعت آن نسبت به زمین برابر صفر است، سرعت فرد نسبت به پلهبرقی نیز برابر خواهد بود. اگر پلهبرقی حرکت کند، چه اتفاقی رخ میدهد؟ در ادامه میخواهیم سرعت پلهبرقی را بهدست آوریم. اگر پله برقی حرکت کند، سرعت آن نسبت به زمین مخالف صفر خواهد بود. سوالی که ممکن است مطرح شود آن است که آیا در این حالت سرعت فرد نسبت به زمین باز هم برابر است، خیر. در این حالت، سرعت فرد نسبت به زمین بسته به اینکه از پلهبرقی بالا میرود یا پایین میآید ممکن است بزرگتر یا کوچکتر از باشد. بنابراین، هنگامی که پلهبرقی حرکت میکند، سرعت فرد نسبت به زمین با سرعت فرد نسبت به پلهبرقی متفاوت است.
هنگامیکه پلهبرقی ساکن است، فرد در مدت زمان از آن بالا میرود. بنابراین سرعت او نسبت به پلهبرقی برابر است با:
در ادامه، اگر پلهبرقی حرکت کند و فرد روی آن بدون حرکت بایستد، در مدت زمان به بالای پلهبرقی میرسد. بنابراین، سرعت پلهبرقی نسبت به زمین برابر بهدست میآید. در قسمت آخر، فرض میکنیم فرد روی پله برقی روشن به بالا میرود. در این حالت میخواهیم مدت زمان رسیدن فرد به بالای پلهبرقی را بهدست آوریم. برای انجام این کار از فرمول سرعت نسبی استفاده میکنیم:
در قسمتهای قبل سرعت فرد نسبت به پلهبرقی و سرعت پلهبرقی نسبت به زمین را بهدست آوردیم. با قرار دادن آنها در رابطه بالا داریم:
پلهبرقی به سمت بالا حرکت میکند و فرد چون عجله دارد از آن با سرعت بالا میرود. در این حالت، زمان رسیدن فرد به بالای پلهبرقی متحرک برابر مسافت طی شده توسط او تقسیم بر سرعت فرد نسبت به زمین است:
با جایگزین کردن در رابطه فوق داریم:
با حذف L از صورت و مخرج کسر و ساده کردن به رابطه زیر برای t میرسیم:
مثال چهارم سرعت نسبی در یک بعد
دو اتومبیل یک و دو در امتداد جاده مستقیم و در یک جهت، به ترتیب با سرعتهای و حرکت میکنند. هنگامیکه دو اتومبیل در فاصله d از یکدیگر قرار گرفتهاند، راننده اتومبیل یک ترمز میکند و اتومبیل با شتاب کندشونده به حرکت خود ادامه میدهد. همزمان، راننده اتومبیل ۲ پای خود را روی پدال گاز میگذارد و اتومبیل ۲ با شتاب تندشونده به حرکت خود ادامه میدهد. اگر باشد، کمینه فاصله اولیه بین دو اتومبیل برای آنکه به یکدیگر برخورد نکنند را بهدست آورید.
پاسخ
با توجه به صورت سوال، دو اتومبیل یک و دو در امتداد جاده مستقیم به ترتیب با سرعتهای و در یک جهت حرکت میکنند. هنگامیکه دو اتومبیل در فاصله d از یکدیگر قرار دارند:
- راننده اتومبیل یک ترمز میکند و اتومبیل با شتاب کندشونده به حرکت خود ادامه میدهد.
- راننده اتومبیل دو پای خود را روی پدال گاز میگذارد و اتومبیل ۲ با شتاب به حرکت خود ادامه میدهد.
ابتدا این مثال را در چارچوب زمین و سپس در چارچوب حرکت نسبی حل میکنیم.
پاسخ در چارچوب زمین
موقعیت دو اتومبیل نسبت به یکدیگر در زمان صفر در تصویر زیر نشان داده شده است. برای حل این مثال، جهت راست را به عنوان جهت مثبت انتخاب میکنیم. از آنجا که اتومبیل یک با شتاب کندشونده حرکت میکند، جهت در خلاف جهت مثبت است. به این نکته توجه داشته باشید که برای حل این سوال در چارچوب حرکت نسبی باید به جهت قراردادی بسیار پایبند باشید و جهت سرعتها و شتابها را متناسب با آن انتخاب کنید.
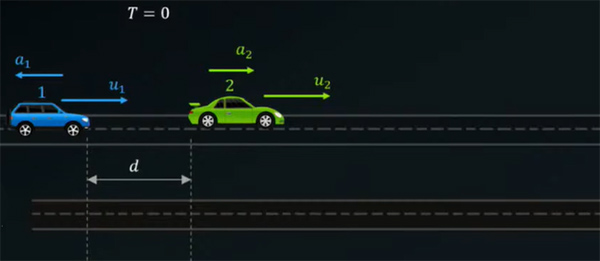
پس از ترمزِ راننده اتومبیل یک و افزایش سرعت اتومبیل دو، چه اتفاقی رخ میدهد؟ اتومبیل یک، مسافت و اتومبیل ۲ مسافت را طی میکنند. در این حالت فرض میکنیم اتومبیل یک در فاصله بسیار نزدیکی نسبت به اتومبیل دو متوقف میشود، اما به آن برخورد نمیکند.
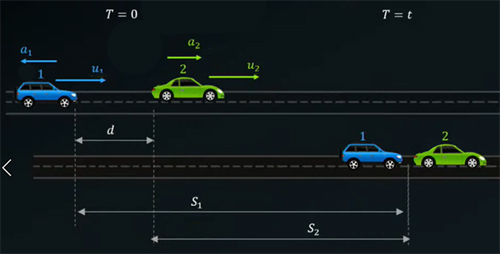
برای جلوگیری از برخورد دو اتومبیل با یکدیگر، سرعت نهایی اتومبیل یک در زمان t چه مقدار باید باشد؟ در زمان t سرعت اتومبیل یک برابر و سرعت اتومبیل 2 برابر میشود. برای آنکه اتومبیل یک به اتومبیل دو برخورد نکند، سرعتهای نهایی دو اتومبیل باید با یکدیگر برابر باشند:
معادله حرکت اتومبیل دو به صورت زیر نوشته میشود:
معادله حرکت اتومبیل یک نیز به صورت زیر نوشته میشود:
علامت منفی برای شتاب در معادله حرکت اتومبیل یک بدان علت است که شتاب آن کندشونده و در خلاف جهت مثبت قرار دارد. با توجه به تصویر نشان داده شده در بالا، تفاضل و برابر d، فاصله اولیه دو اتومبیل از یکدیگر، است. بنابراین، دو معادله حرکت نوشته شده برای دو اتومبیل را از یکدیگر کم میکنیم:
از آنجا که برابر d است، معادله فوق به صورت زیر نوشته میشود:
معادله فوق را برحسب t مرتب میکنیم و به معادله درجه دوم برحسب t میرسیم:
فرض کنید دو اتومبیل با یکدیگر تصادف میکنند، این به چه معنا است؟ هنگامیکه دو اتومبیل با یکدیگر تصادف میکنند، در یک زمان در یک مکان قرار میگیرند. در این صورت معادله جوابی حقیقی دارد. اما همانطور که در صورت مثال گفتیم، به دنبال کمینه فاصله اولیه دو اتومبیل با یکدیگر هستیم تا تصادفی رخ ندهد. بنابراین، معادله فوق نباید جوابی داشته باشد. از ریاضیات دبیرستان به یاد داریم برای آنکه معادلهای درجه دو جوابی نداشته باشد، دلتای آن باید کوچکتر از صفر باشد:
دلتا با استفاده از رابطه زیر بهدست میآید:
در معادله :
مقدارهای فوق را در رابطه قرار میدهیم:
از آنجا که داریم:
۴ از طرفین رابطه بالا حذف میشود. نامعادله فوق را برحسب d حل میکنیم:
بنابراین، کمینه فاصله اولیه دو اتومبیل برای آنکه با یکدیگر تصادف نکندد باید برابر باشد. در این قسمت، کمینه فاصله اولیه دو اتومبیل را در چارچوب زمین بهدست آوردیم. در ادامه، این مثال در در چارچوب حرکت نسبی حل میکنیم.
پاسخ در چارچوب حرکت نسبی
در بخش قبل، زمین را به عنوان چارچوب مرجع انتخاب کردیم. در این قسمت، اتومبیل ۲ را به عنوان چارچوب مرجع انتخاب و دوربینی را به آن متصل و حرکت را از دید این دوربین بررسی میکنیم. آیا اتومبیل دو از دید دوربین متصل به آن حرکت میکند؟ خیر. زیرا دوربین به اتومبیل دو متصل است و همراه با آن حرکت میکند. بنابراین، اتومبیل دو از دید دوربین ساکن است. دوربین اتومبیل یک را میبیند که در فاصله d از اتومبیل دو قرار دارد و به سمت آن حرکت میکند. سوالی که ممکن است مطرح شود آن است که سرعت اتومبیل یک نسبت به چارچوب مرجع جدید چه مقدار است. سرعت اولیه اتومبیل یک نسبت به اتومبیل دو برابر است با:
به این نکته توجه داشته باشید که دو اتومبیل در جهت یکسانی حرکت میکنند و سرعتهای آنها در جهت مثبت قرار دارند. به طور مشابه، شتاب اتومبیل یک نسبت به اتومبیل ۲ به صورت زیر نوشته میشود:
به این نکته توجه داشته باشید که شتابهای اتومبیلهای یک و دو در خلاف جهت یکدیگر قرار دارند. جابجایی اتومبیل یک نسبت به دو نیز با استفاده از رابطه زیر بهدست میآید:
علامت d چیست؟ از آنجا که اتومبیل به سمت جلو حرکت کرده، علامت d مثبت است. در ادامه، مقدار ، سرعت نهایی اتومبیل یک نسبت به اتومبیل دو، را بهدست میآوریم. مقدار این سرعت باید به گونهای باشد که اتومبیل یک با اتومبیل دو تصادف نکند. از دید دوربین متصل به اتومبیل دو، این اتومبیل حرکت نمیکند و ساکن است. بنابراین، از دید این دوربین، اتومبیل یک برای آنکه به اتومبیل دو برخورد نکند، باید قبل از رسیدن به اتومبیل دو و در فاصلهای بسیار نزدیک به آن بایستد. در نتیجه، باید برابر صفر شود.
از آنجا که برابر صفر است، داریم:
در نتیجه، کمینه مقدار d برابر بهدست میآید. همانطور که مشاهده میکنید کمینه مقدار d در چارچوب حرکت نسبی بسیار راحتتر بهدست آمد.
مثال پنجم حرکت نسبی در دو بعد
ماشین پلیسی با سرعت ۳۰ کیلومتر بر ساعت در بزرگراهی حرکت میکند. پلیسی از داخل ماشین گلولهای را به سمت دزدی شلیک میکند که با سرعت ۱۹۲ کیلومتر بر ساعت در جهت حرکت ماشین پلیس از آن دور میشود. اگر سرعت دهانه گلوله برابر ۱۵۰ متر بر ثانیه باشد، سرعت نسبی برخورد گلوله با ماشین دزد را بهدست آورید.
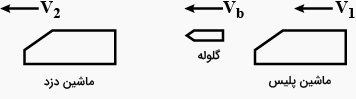
پاسخ
ابتدا سرعت ماشین پلیس و ماشین دزد را به از کیلومتر بر ثانیه به متر بر ثانیه تبدیل میکنیم:
- تبدیل سرعت ماشین پلیس از کیلومتر بر ثانیه به متر بر ثانیه:
- تبدیل سرعت ماشین دزد از کیلومتر بر ثانیه به متر بر ثانیه:
سرعت دهانه، سرعت گلوله نسبت به تفنگ بلافاصله پس از شلیک شدن است. در اینجا سرعت تفنگ مشابه ماشین پلیس است و گلوله در جهت یکسانی با ماشین شلیک میشود.
در رابطه فوق سرعت گلوله نسبت به زمین است. سرعت دهانه برابر ۱۵۰ متر بر ثانیه و سرعت گلوله نسبت به زمین برابر متر بر ثانیه است. در نتیجه، سرعت گلوله نسبت به زمین برابر بهدست میآید. در ادامه، سرعت گلوله نسبت به ماشین دزد را بهدست میآوریم.
مثال ششم حرکت نسبی در یک بعد
تمرین و آزمون
حرکت نسبی در دو بعد چیست ؟
در حالت کلی، حرکت نسبی در دو بعد مشابه حرکت نسبی در یک بعد است، با این تفاوت که حرکت نسبی در دو بعد را به حرکتهای نسبی در یک بعد میشکنیم. به بیان دیگر، باید بردارهای سرعت، شتاب و جابجایی را به مولفههای آن در راستای محورهای افقی و عمودی تجزیه و حرکت نسبی را در راستای افقی و عمودی به صورت جداگانه بررسی کنیم. دو جسم A و B به ترتیب در مکانهای و قرار گرفتهاند. مکان نسبی جسم A نسبت به جسم B برابر است با:
با مشتق گرفتن از طرفین رابطه داریم:
مشتق مکان نسبت به زمان برابر سرعت است، بنابراین سرعت نسبی جسم A نسبت به جسم B در دو بعد به صورت زیر نوشته میشود:
از طرفین رابطه نسبت به زمان مشتق میگیریم:
مشتق سرعت نسبت به زمان برابر شتاب است، بنابراین شتاب نسبی جسم A نسبت به جسم B در دو بعد به صورت زیر نوشته میشود:
مثال حرکت نسبی در دو بعد برای پرتاب توپ در قطار متحرک
قطاری در امتداد خط مستقیم با شتاب ثابت حرکت میکند. پسری داخل قطار ایستاده است. او توپی را با سرعت ۱۰ متر بر ثانیه با زاویه ۶۰ درجه نسبت به افق و نسبت به خود به سمت جلو پرتاب میکند. توپ پس از مدتی به ارتفاع بیشینه میرسد و سپس به سمت پایین فرود میآید. پسر برای گرفتن توپ باید مسافت ۱/۱۵ متر داخل قطار به سمت جلو حرکت کند. شتاب قطار چند متر بر مجذور ثانیه است؟
پاسخ
برای حل این مثال باید بدانیم، شتاب، سرعت و مسافت طی شده نسبت به چه چارچوبی اندازه گرفته شدهاند. برای حل این مثال ابتدا صورت مسئله را با دقت میخوانیم. به هنگام حل مسائل فیزیک، فهمیدن صورت مسئله کمک بزرگی به حل آن میکند. ابتدا در مورد سرعت پرتاب توپ صحبت میکنیم. بر طبق صورت سوال، توپ با زاویه ۶۰ درجه نسبت به افق و با سرعت ۱۰ متر بر ثانیه به جلو پرتاب میشود. این سرعت نسبت به پسر داده شده است. آیا ۱۰ متر بر ثانیه نسبت به چارچوب متصل به قطار اندازه گرفته شده است یا نسبت با چارچوب متصل به زمین؟ پسر داخل قطار است و سرعت او و قطار به هنگام پرتاب توپ با یکدیگر برابر هستند، بنابراین ۱۰ متر بر ثانیه نسبت به چارچوب متصل به قطار داده شده است. در نتیجه، سرعت توپ نسبت به قطار برابر ۱۰ متر بر ثانیه است:
پسر برای دریافت دوباره توپ باید ۱/۱۵ متر به سمت جلو جابجا شود. آیا مسافت طی شده توسط توپ و پسر نسبت به چارچوب متصل به قطار اندازهگیری شده است یا چارچوب متصل به زمین؟ چارچوب مرجع متصل به قطار. بنابراین، جابجایی توپ نسبت به قطار برابر ۱/۱۵ متر است:
بنابراین، حل این مثال در چارچوب مرجع متصل به قطار بسیار راحتتر خواهد بود.
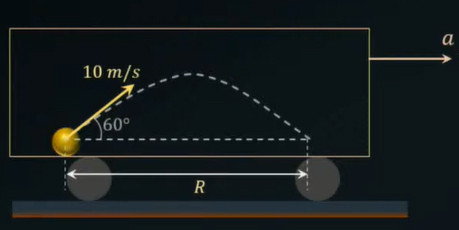
برای حل این مثال از دید ناظر داخل قطار یا نسبت به چارچوب متصل به قطار، دوربینی را داخل واگن قطار میگذاریم. در مورد شتاب حرکت توپ نسبت به قطار چه میتوانیم بگوییم؟ توپ با زاویه ۶۰ درجه نسبت به افق پرتاب میشود. بنابراین، شتاب آن را میتوانیم به مولفههای و تجزیه کنیم. مولفه عمودی شتاب توپ نسبت به قطار برابر است با:
آیا میدانید شتاب عمودی توپ چیست؟ توپ با زاویه ۶۰ درجه نسبت به افق به سمت جلو پرتاب میشود، بنابراین شتاب عمودی آن برابر g است. از آنجا که جهت g به سمت پایین آست، علامت آن را منفی در نظر میگیریم. شتاب قطار در جهت محور عمود چیست؟ قطار به صورت افقی حرکت میکند، بنابراین شتاب آن در جهت y صفر خواهد بود. در نتیجه، برابر است. بنابراین، شتاب توپ در راستای y به صورت زیر نوشته میشود:
در ادامه، شتاب توپ را در راستای افقی بهدست میآوریم:
شتاب توپ در راستای افقی چیست؟ توپ با زاویه ۶۰ درجه نسبت به افق پرتاب میشود. از آنجا که حرکت توپ، حرکت پرتابی است، هیچ شتابی در راستای افقی ندارد. بنابراین، شتاب توپ نسبت به زمین در راستای افقی برابر صفر است، . شتاب قطار در راستای افق چیست؟ همانطور که در صورت سوال گفته شد، قطار با شتاب a در راستای مثبت محور افقی حرکت میکند. بنابراین، شتاب افقی توپ نسبت به قطار برابر است با:
تا اینجا همه چیز را در مورد حرکت توپ نسبت به قطار میدانیم. توپ با زاویه ۶۰ درجه نسبت به محور افقی و با سرعت ۱۰ متر بر ثانیه نسبت به قطار پرتاب میشود. شتاب توپ از دو مولفه تشکیل شده است:
- مولفه عمودی به سمت پایین و برابر g.
- مولفه افقی به سمت چپ و برابر a.
از اینجا به بعد حل سوال بسیار ساده است. سرعت توپ را به مولفههای افقی و عمودی آن به شکل نشان داده شده در تصویر زیر تجزیه میکنیم.
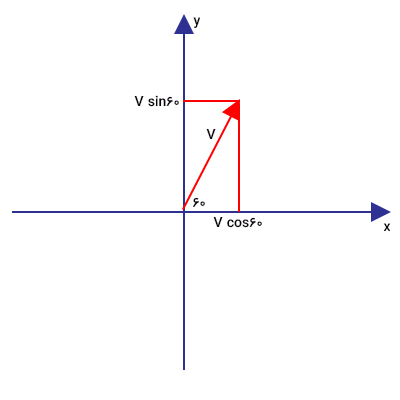
آیا میدانید مدت زمان حرکت توپ در هوا به چه پارامترهایی وابسته است؟ مدت زمان حرکت توپ در هوا، تنها به مولفههای عمودی وابسته خواهد بود. مدت زمان پرواز به صورت زیر بهدست میآید:
در ادامه، جابجایی توپ را بهدست میآوریم. ابتدا جابجایی توپ در راستای افقی را بهدست میآوریم. توپ در راستای افقی به اندازه ۱/۱۵ متر جابجا میشود.
مقدارهای داده شده را در رابطه فوق جایگزین میکنیم:
معادله فوق را برحسب a حل میکنیم و شتاب حرکت قطار را بهدست میآوریم.
مثال حرکت نسبی در دو بعد برای حرکت دو اتومبیل در جاده
کامیونی با سرعت ۷۰ کیلومتر بر ساعت به سمت جنوب حرکت میکند و به تقاطعی نزدیک میشود. همزمان، اتومبیلی با سرعت ۸۰ کیلومتر بر ساعت به سمت شرق حرکت و به تقاطع نزدیک میشود. سرعت اتومبیل نسبت به کامیون را بهدست آورید.
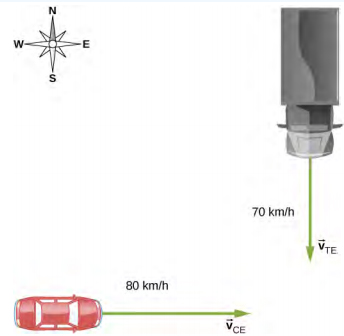
پاسخ
ابتدا چارچوب مرجعی بری کامیون و اتومبیل مشخص میکنیم. برای حل این مثال، زمین را به عنوان چارچوب مرجع در نظر میگیریم. سپس، سرعتهای هر یک از وسیلههای نقلیه را نسبت به چارچوب زمین مینویسیم. با انجام این کار، رابطهای برداری بین سرعتها بهدست میآوریم و سرعت اتومبیل نسبت به کامیون را محاسبه میکنیم. اتومبیل در راستای محور و از غرب به شرق حرکت میکند. جهت راست یا شرق را جهت مثبت در نظر میگیریم. از آنجا که اتومبیل به سمت راست حرکت میکند، جهت آن مثبت خواهد بود. از اینرو، سرعت اتومبیل نسبت به زمین برابر است با:
کامیون در راستای محور و از شمال به جنوب حرکت میکند. جهت شمال یا بالا را جهت مثبت در نظر میگیریم. از آنجا که کامیون به سمت جنوب حرکت میکند، جهت آن منفی خواهد بود. از اینرو، سرعت کامیون نسبت به زمین برابر است با:
سرعت اتومبیل نسبت به کامیون را با استفاده از قانون جمع بردارهای به صورت زیر مینویسیم:
در معادله فوق:
- سرعت اتومبیل نسبت به کامیون است.
- سرعت اتومبیل نسبت به زمین است.
- سرعت زمین نسبت به کامیون است.
همانطور که در ابتدای حل این مثال عنوان شد زمین به عنوان چارچوب مرجع انتخاب شده است. در این مثال، سرعت کامیون نسبت به زمین داده شده است. قرینه بردار سرعت زمین نسبت به کامیون برابر بردار سرعت کامیون نسبت به زمین است:
نمودار برداری معادله در تصویر زیر نشان داده شده است.
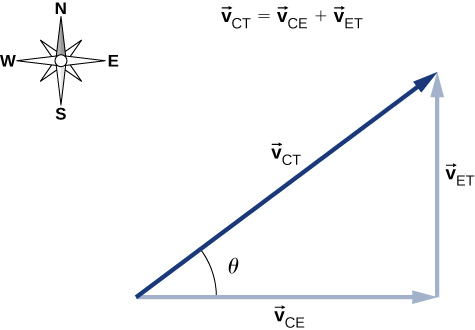
با توجه به تصویر زیر، سرعت اتومبیل نسبت به کامیون به صورت زیر بهدست میآید:
زاویه نیز به صورت زیر بهدست میآید:
مثال حرکت نسبی در دو بعد برای حرکت هواپیما و وزش باد
خلبانی برای رسیدن به مقصد باید هواپیما را به سمت شمال هدایت کند. هواپیما میتواند با سرعت ۳۰۰ کیلومتر بر ساعت در هوای آرام حرکت کند. باد با سرعت ۹۰ کیلومتر بر ساعت به سمت شمالشرق میوزد.
- سرعت هواپیما نسبت به زمین را بهدست آورید.
- خلبان برای آنکه به سمت شمال پرواز کند، هواپیمای خود را در چه جهتی باید حرکت دهد؟
پاسخ
اگر باد نمیوزید، خلبان به راحتی میتوانست هواپیما را به سمت شمال حرکت دهد. اما باد با سرعت بالای ۹۰ کیلومتر بر ساعت در راستای شمال شرق میوزد. به همین دلیل، هواپیما نمیتواند با قرار گرفتن در راستای شمال، در همان راستا به راه خود ادامه دهد. در نتیجه، خلبان باید هواپیما را در جهتی بین شمال و شرق قرار دهد تا تغییر مسیر آن به دلیل وزیدن باد جبران شود. باید معادله برداری متشکل از سرعت هواپیما نسبت به زمین، سرعت هواپیما نسبت به هوا و سرعت هوا نسبت به زمین بنویسیم. از آنجا که سرعتهای هواپیما نسبت به هوا و هوا نسبت به زمین را میدانیم، به راحتی میتوانیم سرعت هواپیما نسبت به زمین را بهدست آوریم. با رسم بردارها در نمودار برداری میتوانیم سرعت خواپیما نسبت به زمین را محاسبه کنیم.
همچنین، با استفاده از نمودار برداری میتوان زاویه سرعت هواپیما نسبت به شمال را بهدست آوریم. این زاویه مسیر حرکت هواپیما را به ما نشان میدهد. معادله برداری به صورت زیر نوشته میشود:
در معادله فوق:
- سرعت هواپیما نسبت به زمین است.
- سرعت هواپیما نسبت به هوا است.
- سرعت هوا نسبت به زمین است.
بردارهای فوق در تصویر زیر نشان داده شدهاند.
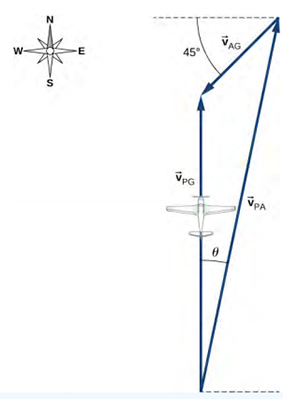
اندازه سرعتهای هواپیما نسبت به هوا و هوا نسبت به زمین به ترتیب برابر ۳۰۰ کیلومتر بر ساعت و ۹۰ کیلومتر بر ساعت است. این دو سرعت را در معادله حرکت جایگزین و سرعت هواپیما نسبت به زمین را برابر ۲۳۰ کیلومتر بر ساعت بهدست میآوریم. همچنین، زاویه برابر است با:
مثال حرکت نسبی در دو بعد برای قایق در رودخانه
عرض رودخانهای برابر ۴۰ متر است. آب با سرعت ثابت ۶ متر بر ثانیه از چپ به راست نسبت به چارچوب مرجع در نقطه O حرکت میکند. قایقی میخواهد از عرض رودخانه عبور کند و از نقطه A به نقطه B برود. بردار سرعت قایق نسبت به رودخانه برابر است. موتورسواری با سرعت ثابت ۲ متر بر ثانیه نسبت به O از شمال به جنوب حرکت میکند و از پل روی رودخانه عبور میکند. کمیتهای زیر را بهدست آورید:
- بردار سرعت قایق نسبت به نقطه O
- بردار سرعت قایق نسبت به موتورسوار
- مدت زمان عبور قایق از رودخانه
- فاصله بین نقطه A تا B
- اگر سرعت آب دو برابر شود، قایق در چه مدت زمانی عرض رودخانه را طی میکند؟
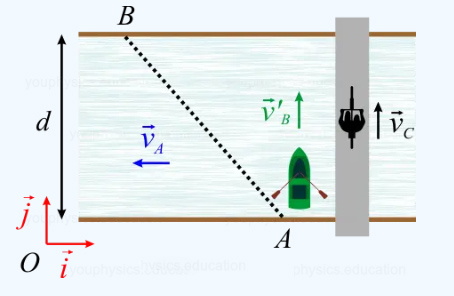
پاسخ
ابتدا سرعتهای داده شده را به صورت برداری مینویسیم. برای انجام این کار جهت بالا و راست را به عنوان جهتهای مثبت در راستای عمودی و افقی انتخاب میکنیم.
- آب در رودخانه با سرعت ثابت ۶ متر بر ثانیه به سمت چپ حرکت میکند. بنابراین، علامت سرعت، منفی و بردار سرعت آن به صورت زیر نوشته میشود:
- قایق با سرعت ثابت ۴ متر بر ثانیه به سمت بالا حرکت میکند. بنابراین، علامت سرعت قایق، مثبت و بردار سرعت آن به صورت زیر نوشته میشود:
- موتورسوار با سرعت ثابت ۲ متر بر ثانیه روی پل به سمت شمال حرکت میکند. بنابراین، علامت سرعت آن مثبت و بردار سرعت آن به صورت زیر نوشته میشود:
در این مثال سرعتهایی داریم که نسبت به دو چارچوب مرجع اندازه گرفته میشوند.
- چارچوب مرجع O که ساکن است.
- آب رودخانه که حرکت میکند و آن را مینامیم.
با سرعت ثابت نسبت به O حرکت میکند. به این نکته توجه داشته باشید که هر دو چارچوب مرجع، لخت هستند. تبدیل گالیله برای سرعت به صورت زیر نوشته میشود:
در رابطه فوق:
- سرعت نسبت به چارچوب مرجع ساکن است.
- سرعت اندازهگیری شده نسبت به چارچوب مرجعی است که با سرعت ثابت نسبت به چارچوب اول حرکت میکند.
بنابراین، در معادله ، سرعت قایق نسبت به O برابر و سرعت قایق نسبت به آب برابر یا خواهد بود. سرعت حرکت چارچوب مرجع نسبت به چارچوب ساکن است. در این مثال، برابر سرعت آب نسبت به O یا خواهد بود. در بخش یک میخواهیم سرعت قایق نسبت به چارچوب مرجع O را بهدست آوریم:
با جایگذاری مقدارهای داده شده در این رابطه داریم:
قسمت ۲: در این قسمت بردار سرعت قایق نسبت به موتورسوار را بهدست میآوریم. در این حالت، موتورسوار چارچوب مرجع متحرک، است:
قسمت ۳: برای آنکه بدانیم قایق در چه مدت زمانی عرض رودخانه را طی میکند، از عرض داده شده، d، و مولفه عمودی سرعت قایق نسبت به O استفاده میکنیم:
قسمت ۴: در این قسمت فاصله بین نقطه A تا B را بهدست میآوریم. از زمان محاسبه شده در قسمت ۳ میتوانیم فاصله افقی طی شده توسط قایق را محاسبه کنیم. برای محاسبه فاصله افقی از مولفه افقی سرعت قایق استفاده میکنیم:
برای محاسبه فاصله بین نقطههای A و B از قضیه فیثاغورت استفاده میکنیم:
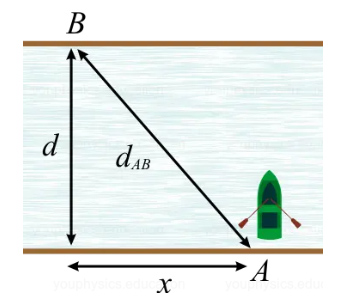
قسمت ۵: اگر سرعت حرکت آب رودخانه دو برابر میشد، قایق باز هم در مدت زمان یکسانی عرض رودخانه را طی میکرد. زیرا مولفه عمودی سرعت تغییر نمیکرد.
جمعبندی
در این مطلب، در مورد حرکت نسبی در یک و دو بعد به همراه حل مثالهای متنوع صحبت کردیم. انتخاب مرجع در حرکت نسبی بسیار مهم است. بنابراین، به هنگام حل مسائل مربوط به حرکت نسبی باید ابتدا نکتههای زیر را در نظر بگیریم:
- مسئله را با دقت بخوانی.
- طرحی ساده از مسئله رسم و سعی کنیم چارچوبهای مرجع را با دقت انتخاب کنیم.
- مقدارهای داده شده و خواسته شده را یادداشت کنیم.












