انرژی کوانتومی چیست؟ — به زبان ساده

انرژی کوانتومی یا «کوانتای انرژی» (Energy Quantization) به تراز‌های انرژی در سطوح زیر اتمی مربوط می‌شود. در فیزیک مدرن انرژی را به صورت بسته‌های گسسته‌ای به نام فوتون توصیف می‌کنند. در این مطلب با مفهوم انرژی کوانتومی آشنا می‌شویم و به پرسش انرژی کوانتومی چیست پاسخ می‌دهیم.

انرژی کوانتومی چیست ؟

فرض کنید لباسی را به قیمت بیست هزار تومان خریده‌اید. به هنگام پرداخت پول از اسکناس‌های ده هزار تومانی یا پنج هزار تومانی استفاده می‌کنید. اما اسکناس سه یا چهار هزار تومانی ندارید. بنابراین، پول را کمیتی کوانتومی می‌دانیم. به بیان ساده‌تر، مقادیر آن گسسته است.

فیلم آموزش مکانیک کوانتومی 1 – جامع و با نکات کاربردی در فرادرس

کلیک کنید

سوالی که ممکن است مطرح شود آن است که مفهوم کوانتوم در فیزیک چیست و چه کمیت‌هایی در فیزیک گسسته هستند.

کوانتوم چیست ؟

کوانتوم کلمه‌ای لاتین برای مقدار است. در مفهوم مدرن، به کوچک‌ترین واحد گسسته ممکن برای هر کمیت فیزیکی مانند انرژی یا ماده، کوانتوم گفته می‌شود. این مفهوم برای نخستین بار توسط فیزیکدان آلمانی بهانرژی کوانتوم تاچ چیس نام «ماکس پلانک» (Max Planck) استفاده شد. او به هنگام توضیح تابش جسم سیاه از لفظ کوانتوم استفاده کرد.

تابش جسم سیاه چیست ؟

در بعضی سیستم‌ها، انرژی کوانتیزه یا گسسته است. این جمله به این معنی است که نه هر مقداری، بلکه مقدارهای عددی مشخصی به انرژی نسبت داده می‌شود. حالت بیان شده برخلاف فیزیک کلاسیک است. در فیزیک نیوتونی، انرژی می‌تواند هر مقداری داشته باشد. سوالی که ممکن است مطرح شود آن است که اگر در فیزیک کلاسیک انرژی گسسته باشد چه اتفاقی رخ خواهد داد.

فرض کنید انرژی جنبشی ماشین در حال حرکتی گسسته است. از آنجایی که جرم ماشین در حال حرکت ثابت است، تنها مقدار متغیر سرعت خواهد بود. در نتیجه ماشین نمی‌تواند با هر سرعتی حرکت کند و فقط با سرعت‌های مشخصی حرکت خواهد کرد. آیا سرعت حرکت ماشین واقعا کمیتی گسسته است؟ پاسخ به این سوال خیر است.

با مفهوم کوانتوم در سیستم‌هایی مانند اتم‌ها و مولکول‌ها آشنا هستیم، اما مفهوم انرژی کوانتومی را کمتر شنیده‌ایم. در حالی‌که اولین نشانه‌های پیدایش فیزیک کوانتوم، انرژی کوانتومی بود. آیا می‌دانید انرژی کوانتومی در چه سیستم‌هایی مشاهده شده است؟ در ادامه به این پرسش پاسخ خواهیم داد.

تابش و جذب امواج الکترومغناطیسی را در نظر بگیرید. بر طبق پیش‌بینی فیزیک کلاسیک، اجسام با دمای بالا انرژی الکترومغناطیسی را به شکل پیوسته منتشر می‌کنند. به بیان دیگر، نور با هر طول موجی منتشر می‌شود. سال‌ها بعد پلانک با بررسی تابش جسم با دمای بالا یا تابش جسم سیاه، این نظریه را رد کرد.

طول موج انرژی منتشر شده توسط جسم تنها به دما بستگی دارد. بنابراین، مشعل اجاق برقی یا فیلامان بخاری‌ها هنگامی که گرم می‌شوند به رنگ قرمز مات یا نارنجی درمی‌آیند. در حالی‌که، سیم تنگستن با دمای بسیار بالاتر در لامپ، به رنگ زرد دیده می‌شود.

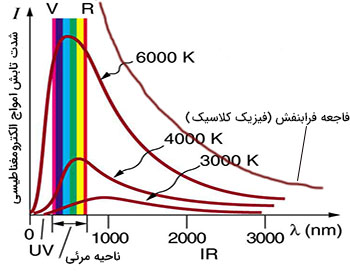
شدت تابش به صورت انرژی تابیده شده بر واحد سطح تعریف می‌شود. شدت تابش جسم سیاه بر حسب طول موج در دماهای متفاوت در تصویر زیر نشان داده شده است. در فیزیک کلاسیک یک فرضیه اساسی برای تابش جسم سیاه در نظر گرفته شده بود:

• افزایش یا کاهش انرژی به صورت منحنی صاف و پیوسته رخ می‌دهد. به عنوان مثال، با کاهش طول موج، شدت تابش جسم به صورت پیوسته، بدون هیچ محدودیتی در دما افزایش می‌یابد.

بنابراین، فیزیک کلاسیک قادر به توضیح کاهش شدید شدت تابش در طول موج‌های کوتاه‌تر نبود (فاجعه فرابنفش). در سال 1900، پلانک با فرض کردن مقادیر گسسته برای انرژی الکترومغناطیسی، فاجعه فرابنفش را توضیح داد. بر طبق فرضیه او، در هر دمایی، مقدار بیشینه‌ای برای شدت تابش جسم سیاه وجود دارد. بنابراین، شدت تابش جسم سیاه به صورت منحنی صاف و افزایشی نخواهد بود. در نتیجه، انرژی به صورت مضربی از کوچک‌ترین واحد انرژی به نام کوانتوم مبادله می‌شود.

معادله انرژی کوانتومی چیست ؟

مفهوم انرژی کوانتومی در نگاه اول ناآشنا به نظر می‌رسد اما با این عبارت بارها مواجه شده‌ایم. پلانک به منظور به دست آوردن رابطه ریاضی برای انرژی تابیده شده از جسم سیاه، فرض کرد مولکو‌ل‌ها داخل جسم مانند فنر عمل می‌کنند.

فیلم آموزش مکانیک کوانتومی 1 – مرور و حل تمرین در فرادرس

کلیک کنید

این فنرها تابش را جذب یا منتشر می‌کنند. به منظور توصیف طیف تابشی جسم سیاه، انرژی اتم‌ها و مولکول‌های نوسان‌کننده باید کوانتیزه باشد. از این‌‌رو، انرژی نوسان‌گری با فرکانس ‌f به صورت زیر نوشته می‌شود:

$$E= (n \ +\ \frac{1}{2})hf$$

در رابطه بالا مقادیر n برابر صفر، یک، دو، و ... است. همچنین، h ثابت پلانک نام دارد و مقدار آن برابر $$6.626 \ \times \ 10^{-34} \ J.s$$ خواهد بود.

معنای رابطه نوشته شده برای انرژی به صورت زیر است:

انرژی نوسان‌گر با فرکانس ‌f (تابش یا جذب تشعشع موج الکترومغناطیسی با فرکانس f) تنها به صورت گسسته و با گام‌های $$\triangle E = hf$$ افزایش یا کاهش می‌یابد. 

به منظور داشتن درک بهتری از مفهوم انرژی کوانتومی، مثال‌هایی از انرژی کوانتومی در سیستم ماکروسکوپیک ارائه می‌شود. آونگی را در نظر بگیرید که تنها با دامنه‌هایی با مقادیر مشخص نوسان ‌می‌کند. انرژی کوانتومی همچنین در موج ایستاده در طناب نیز مشاهده می‌شود. در این سیستم هارمونیک‌های مشخصی اجازه انتشار دارند. همچنین حالتی را در نظر بگیرید که از پله‌های ساختمانی بالا می‌روید. در این حالت انرژی پتانسیل گرانشی به صورت گسسته تغییر می‌کند. در واقع تفاوت انرژی پتانسیل به تعداد پله‌هایی که بالا رفته‌اید بستگی دارد.

مثال انرژی کوانتومی

انرژی فوتون نور سبز با فرکانس $$5.75\times10^{14}$$ چه مقدار است؟

پاسخ:

قبل از حل این مثال ابتدا فوتون را تعریف می‌کنیم. فوتون ذره تابش الکترومغناطیسی (نور) با جرم صفر است که یک کوانتوم انرژی را حمل می‌کند.

داده‌های مثال به صورت زیر داده شده است:

$$f = 5.75 \times 10^{14} \ Hz \\ h = 6.626 \times 10^{-34} \ J.s$$

رابطه انرژی کوانتومی به صورت زیر نوشته می‌شود:

$$E=hf$$

 با قرار دادن داده‌ها در رابطه بالا داریم:

$$E = (6.626 \ \times \ 10^{-34} \ J.s) \ \times \ (5.75 \ \times \ 10^{14} \ Hz) = 3.81 \ \times \ 10^{-19} \ J$$

همان‌طور که می‌بینید انرژی به دست آمده بسیار کوچک به نظر می‌رسد. اما مقدار به دست آمده، انرژی یک فوتون نور است. نور مرئی از تعداد بسیار زیادی فوتون تشکیل شده است.

انرژی کوانتومی الکترون چیست ؟

حرکت الکترون آزاد نیست. الکترون توسط نیروی جاذبه به هسته اتم مقید است. بر طبق پیش‌بینی مکانیک کوانتوم انرژی کل الکترون کوانتیزه است و به صورت زیر نوشته می‌شود:

$$E_n = \frac{-2 \pi^2 m e^4 Z^2}{n^2 h^2} \ \ (n = 1,2,3,4, ...)$$

فیلم آموزش مروری مکانیک کوانتومی 2 در فرادرس

کلیک کنید

برای رابطه بالا داریم:

• n: عدد کوانتومی
• m: جرم الکترون
• e: بزرگی بار الکترون
• h: ثابت پلانک
• Z: عدد اتمی (تعداد بارهای مثبت داخل هسته).

رابطه بالا برای هر اتم یا یون تک الکترونی صدق می‌کند. به عنوان مثال، $$He^+$$ سیستمی تک الکترونی با عدد اتمی برابر دو است. برای این سیستم می‌توانیم نمودار تراز انرژی را به صورت زیر رسم کنیم. هر خط نشان‌دهنده مقدار مجاز انرژی است.

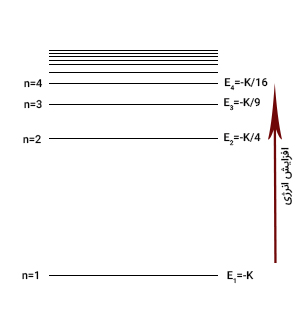
در تصویر بالا تمام ثابت‌ها داخل ثابت کلی به نام ‌K گذاشته شده‌اند. بنابراین رابطه انرژی به صورت زیر به دست خواهد آمد:

$$E_n = \frac{-K}{n^2} \ (n=1,2,3,...)$$

از آنجایی که در سیستم واقعی حرکت الکترون در سه بعد اتفاق می‌افتد، بنابراین باید سه عدد کوانتومی برای اتم هیدروژن در نظر گرفته شود. اما، مقدار انرژی، تنها به عدد کوانتومی کلی n بستگی دارد. بنابراین به ‌n عدد کوانتومی اصلی گفته می‌شود. در این حالت، مقدار انرژی متناسب با عکس $$n^2$$ است. با افزایش مقدار n، انرژی مثبت‌تر و فاصله خطوط انرژی کمتر می‌شود.

هنگامی که مقدار ‌n به سمت بی‌نهایت میل می‌کند، مقدار انرژی صفر می‌شود. در این هنگام الکترون از قید انرژی جاذبه هسته آزاد می‌شود و آزادانه حرکت می‌کند. فاصله متوسط بین هسته و الکترون (r) با افزایش ‌n و در نتیجه انرژی، افزایش می‌یابد. بنابراین، به منظور رهاسازی الکترون از قید هسته انرژی باید به اندازه کافی بزرگ باشد.

تفات انرژی $$E_1$$ و $$E_{\infty}$$ عبارت است از:

$$E_{\infty} - E_1 = 0 - (-K) = K = \frac{2\pi ^2me^4 }{h^2} = \frac{e^2}{2a_0}$$

به این تفاوت انرژی، انرژی یونش گفته می‌شود. به مقدار انرژی لازم برای آزاد کردن کامل الکترون از قید هسته انرژی یونش می‌گوییم. در نتیجه داریم:

$$H \rightarrow H^+\ + e^- \ \ (\triangle E = K= 13.60 \ eV = \frac{1}{2} \ au)$$

مقدار انرژی محاسبه شده در بالا برای آزاد کردن الکترون از قید هسته کافی است. اگر مقدار انرژی داده شده به الکترون از K بیشتر باشد، الکترون پس از آزاد شدن مقداری انرژی جنبشی نیز به دست می‌آورد. هنگامی که الکترون از قید هسته آزاد می‌شود، با هر سرعنی می‌تواند حرکت کند. بنابراین انرژی آن می‌تواند هر مقداری داشته باشد. در این حالت، مقادیر انرژی الکترون پیوسته است.

طیف اتمی

اکنون به انتشار و جذب تابش الکترومغناطیسی توسط گازها توجه می‌کنیم. خورشید یکی از بهترین مثال‌‌ها برای این حالت است. مطالعه انتشار گاز‌های داغ در حدود دو قرن قبل شروع شد. با مطالعه طیف‌های تابش گازها اطلاعات بسیار زیادی در مورد اتم‌ها به دست می‌آوریم. به عنوان مثال، نوع گاز و دمای آن مشخص می‌شود.

این تابش‌های الکترومغناطیسی ناشی از انتقال الکترون‌ها بین ترازهای انرژی اتم‌ها و مولکول‌های تکی است. بنابراین، به این طیف‌ها، طیف‌های اتمی می‌گوییم. تصویر زیر نمونه‌ای از طیف تابشی اکسیژن را نشان می‌دهد.

یکی از مهم‌ترین مشخصه‌های این طیف‌ها، گسستگی آن‌ها است. این گسستگی بدان معنا است که تنها طول موج‌ها و در نتیجه آن فرکانس‌های مشخصی منتشر می‌شوند. اگر انرژی و فرکانس به صورت زیر با یکدیگر رابطه داشته باشند:

$$\triangle E = hf$$

آن‌گاه انرژی الکترون‌ها در اتم‌ها و مولکول‌های تابشی گسسته است.

طیف اتم هیدروژن

لوله شیشه‌ای پر شده از گاز هیدروژن را در نظر بگیرید. در صورت اعمال ولتاژ، نور رنگی از نمونه تابیده می‌شود. انرژی الکتریکی، بسیاری از مولکول‌های هیدروژن را به اتم‌ها تبدیل می‌کند.

$$H_2 \rightarrow H+H$$

الکترون‌های داخل اتم‌ها و مولکول‌ها پس از جذب انرژی به ترازهای انرژی بالاتر منتقل می‌شوند. همچنین یونیزاسیون گاز نیز اتفاق می‌افتد. به حالتی که در آن الکترون در تراز انرژی بالاتر از پایین‌ترین تراز قرار داشته باشد، حالت برانگیخته می‌گوییم. طول عمر حالت برانگیخته بسیار کم و از مرتبه بزرگی $$10^{-8}$$ ثانیه است. الکترون با رفتن به تراز انرژی پایین‌تر، انرژی از دست می‌دهد. ذکر این نکته مهم است که الکترون هم‌زمان با از دست دادن انرژی، فوتون نیز تابش می‌کند.

مقدارهای فرکانس‌های فوتون‌های تابشی با استفاده از تفاوت انرژی بین دو تراز محاسبه می‌شوند:

$$f=\frac{\triangle E}{h} = \frac{E_{n^{'}}-E_n}{h} \ \ (n^{'} >n)$$

فرض کنید هنگامی که الکترون به پایین‌ترین تراز انرژی می‌رود، تمام فرکانس‌های ممکنه را در نظر می‌گیریم:

$$f=\frac{\triangle E}{h} = \frac{E_{n^{}}-E_1}{h} = \frac{K}{h}(\frac{1}{1}-\frac{1}{n^2}) \ (n=2,3,...)$$

با جایگذاری هر مقدار ‌n در رابطه فوق، مقدار مشخصی ‌‌برای ‌f به دست خواهد آمد.

فرمول ریدبرگ

در مطالب فوق گفتیم در صورتی که الکترون از تراز انرژی بالاتر به تراز انرژی پایین‌تر بیاید، فوتون تابش خواهد کرد. اگر الکترون از تراز انرژی پایین‌تر به تراز انرژی بالاتر برود، فوتون توسط اتم جذب می‌شود. فرکانس یا طول موج فوتون جذب شده یا تابشی توسط فرمول ریدبرگ به صورت زیر به دست می‌آید:

$$f = \frac{1}{\lambda} R (\frac{1}{n_1^2}-\frac{1}{n_2^2})$$

در رابطه بالا $$n_1$$ و $$n_2$$ اعداد طبیعی هستند و $$n_2$$ همیشه از $$n_1$$ بزرگتر است. همچنین به R ریدبرگ گفته می‌شود و به طور معمول با $$R_H$$ نشان داده می‌شود.

مثال معادله ریدبرگ

اگر $$n_1 = 3$$ و $$n_2 = 4, 5, ...$$ باشند، فرکانس و طول موج مربوط به دومین تراز انرژی را به دست آورید.

پاسخ:

اعداد داده شده برای n، سری پاشن نامیده می‌شود. در اینجا دومین خط این سری را محاسبه می‌کنیم.

$$(n_1 = 3 , n_2 = 5) \\ f=\frac{1}{\lambda}=109680 (\frac{1}{3^2} - \frac{1}{5^2})cm^{-1} = 7.799 \times10^3 \ cm^{-1} \\ \lambda = 1.282 \times10^{-4} \ cm = 1282 \ nm$$

مقدار به دست آمده برای طول موج در نزدیکی ناحیه فروسرخ یا مادون قرمز قرار دارد.

معرفی فیلم آموزش مکانیک کوانتومی ۱

مجموعه فرادرس در تولید و محتوای آموزشی خود اقدام به تهیه فیلم آموزش فیزیک کوانتومی ۱ برای دانش‌جویان سال دوم و سوم علوم پایه رشته‌های فیزیک و شیمی کرده که این مجموعه آموزشی از شش درس تشکیل شده است.

در درس یکم مبحث تابش جسم سیاه، مدل‌های مشخصه در داخل یک کاواک، نظریه کوانتومی پلانک و نظریه کوانتومی ماده تدریس می‌شود. در این مطلب با تابش جسم سیاه و انرژی کوانتومی آشنا شدید. پس از دیدن درس یکم این فیلم آموزشی، درک عمیق‌تری از این مفاهیم خواهید داشت. مباحث مربوط به شکل نیوتنی مکانیک، معادلات لاگرانژ و دینامیک نسبیتی در درس دوم آموزش داده خواهد شد. برای مقایسه فیزیک کلاسیک و فیزیک نیوتونی دیدن درس دوم توصیه می‌شود. با صورت‌بندی مکانیک کوانتومی، عملگرها و اصول موضوع‌ مکانیک کوانتومی در درس‌ سوم آشنا می‌شوید.

درس چهارم در مورد مکانیک موجی در یک بعد است. در این درس رفتار کوانتومی ذره در یک‌بعد و انرژی‌ آن توضیح داده می‌شود. همچنین در مورد انواع انرژی‌ها به اختصار توضیح داده شد. در پایان، با مکانیک موجی در سه‌بعد و ذرات بدون برهم‌کنش بیشتر آشنا می‌شوید.

• برای دیدن فیلم آموزش مکانیک کوانتومی ۱ + اینجا کلیک کنید. 

تاکنون با مفهوم انرژی کوانتومی چیست آشنا شدیم، در ادامه به سوال‌هایی در زمینه انرژی کوانتومی پاسخ می‌دهیم.

معنای کوانتوم در فیزیک کوانتوم چیست ؟

کلمه کوانتوم از کلمه‌ لاتین quantus به معنای چقدر خوب می‌آید. در فیزیک کوانتوم تمام پدیده‌های فیزیکی مانند انرژی و تکانه، گسسته هستند و مقادیر آن‌ها مضربی از مقدار کوچکی به نام کوانتوم است. به عنوان مثال، فوتون ذره نور و انرژی آن برابر E=hf است. این انرژی کوانتوم فوتون است. در این صورت، اگر فوتون‌هایی را با فرکانس ‌f در نظر بگیرید، مقدارهای انرژی آن‌ها تنها برابر با 2hf، ۳hf و ... خواهند بود.

ثابت پلانک چیست ؟

پلانک و دیگر فیزیکدان‌ها در اواخر قرن 19 و اوایل قرن ۲۰ در تلاش بودند تفاوت میان فیزیک کلاسیک و فیزیک کوانتوم را بفهمند. فیزیک کلاسیک در مورد حرکت اجسام در جهان اطرافمان است. در حالی‌که فیزیک جدید در مورد جهانی بسیار کوچک و غیرقابل‌مشاهده است. انرژی در فیزیک کوانتوم گاهی مانند موج و گاهی مانند ذره‌ای به نام فوتون رفتار می‌کند.

در مکانیک کوانتوم، فیزیک با تجربه ما از جهان ماکروسکوپیک بسیار تفاوت دارد. کودکی را در حال تاب‌سواری در نظر بگیرید. در فیزیک کلاسیک کودک، تاب را تا هر ارتفاعی که بتواند بالا می‌برد. انرژی این سیستم متناسب با مجذور دامنه است. بنابراین، کودک در هر محدوده انرژی تاب‌سواری می‌کند. اما هنگامی که به محدوده فیزیک کوانتومی می‌رویم چه اتفاقی می‌افتد؟ در اینجا رفتار اجسام به طور کامل متفاوت است.

مقدارهای انرژی نوسان‌گر مانند پله‌های نردبان گسسته است. ترازهای انرژی به صورت hf از هم جدا شده‌اند. در اینجا، f فرکانس فوتون (ذره نور) است.

در سال 2016 فیزیکدانی به نام «Darine El Haddad» (دارین حداد) ثابت پلانک را با استفاده از استعاره ریختن شکر در چای توضیح داد. در فیزیک کلاسیک انرژی پیوسته است. این جمله بدان معنا است که اگر قاشق پر از شکری داشته باشیم، هر مقدار شکر بخواهیم می‌توانیم داخل لیوان چای بریزیم. از این استعاره می‌توان نتیجه گرفت که در فیزیک کلاسیک هر مقدار انرژی پذیرفتنی است. اما ماکس پلانک نگاه عمیق‌تری داشت. بر طبق نظر او انرژی گسسته است. در این صورت تنها می‌توان یک، دو یا سه قاشق شکر به چای اضافه کرد. در نتیجه، انرژی تنها مقادیر مشخصی دارد.

ثابت پلانک مقدار انرژی فوتون را به فرکانس آن ربط می‌دهد. تابش الکترومغناطیسی و ذرات بنیادی به طور ذاتی ویژگی‌های ذره و موج را از خود نشان می‌دهند. ثابت بنیادی پلانک این دو رفتار (ذره‌ای و موجی) را به یکدیگر متصل می‌کند.

نکته عجیبی در مورد ثابت پلانک وجود دارد. مقدار آن با گذر زمان به اندازه بسیار کوچکی تغییر کرده است. در سال ۱۹۸۵ مقدار پذیرفته شده برای این ثابت برابر $$6.626176 \times 10^{-34} \ J.s$$ بود. این عدد در سال ۲۰۱۸ بار دیگر محاسبه شد و مقدار $$6.62607015 \times 10^{-34} \ J.s$$ به دست آمد. ذکر این نکته مهم است که مقدار همه ثابت‌های فیزیکی در جهان ثابت هستند ولی ما مقدار دقیق آن‌ها را نمی‌دانیم. برای اندازه‌گیری این ثابت‌ها آزمایش‌هایی طراحی می‌شوند. در نتیجه مقدار به دست آمده برای ثابت پلانک از آزمایش‌های انجام شده و میانگین‌گیری به دست آمده است.

اگر مقدار ثابت پلانک از عدد گفته شده بسیار بزرگ‌تر یا کوچک‌تر بود، آن‌گاه جهان اطراف ما کاملا متفاوت از جهان کنونی بود. به عنوان مثال اگر مقدار آن زیاد می‌شد، اندازه اتم‌های ثابت چندین برابر ستاره‌ها می‌شد.

اگر مقدار ثابت پلانک برابر $$6.62 \times 10^{-20} \ J.s$$ بود چه رخ می‌داد ؟

ثابت پلانک عدد مهمی در فیزیک کوانتوم است. با افزایش مقدار عدد ثابت پلانک تغییرات زیادی در اطرافمان رخ می‌داد. ممکن بود هیچ اتمی در جهان نباشد. انرژی لازم برای یونیزه کردن اتم هیدروژن متناسب با $$\frac{1}{h^2}$$ است. در نتیجه اگر مقدار ثابت پلانک به اندازه $$10^{14}$$ برابر افزایش پیدا کند، انرژی یونیزاسیون هیدروژن به اندازه $$10^{-28}$$ کاهش می‌یابد. بنابراین، اتم با کوچک‌ترین تحریک یونیزه خواهد شد.

حتی اگر اتم‌های پایداری وجود داشته باشند، اندازه آن‌ها بسیار بزرگ خواهد بود. اندازه شعاع اتم با مجذور h رابطه مستقیم دارد. در نتیجه اندازه اتم از $$0.53 \times 10^{-10}$$ متر به $$0.53 \times 10^{18}$$ متر افزایش خواهد یافت. این مقدار در حدود ۱۰۰ برابرِ فاصله نزدیک‌ترین ستاره است. بنابراین با افزایش ثابت پلانک، در جهان بسیار متفاوتی زندگی می‌کردیم.

جمع‌بندی

در این مطلب در مورد انرژی کوانتومی صحبت کردیم و به پرسش انرژی کوانتومی چیست پاسخ دادیم. همچنین با تابش جسم سیاه و طیف اتم هیدروژن آشنا شدیم. گفتیم در فیزیک کوانتوم مقدارهای نسبت داده شده به انرژی گسسته است و با رابطه E=hf به دست می‌آید. در این رابطه ثابت جهانی به نام ثابت پلانک وجود دارد که مقدادر عددی آن بسیار مهم است. با افزایش یا کاهش مقدار آن، جهانی که اکنون می‌شناسیم به طور کامل تغییر می‌کرد.