اتحاد مربع دو جمله ای چیست؟ – اثبات، فرمول و حل تمرین و مثال

در آموزش‌های پیشین مجله فرادرس، با اتحادها آشنا شدیم و دیدیم که یکی از کاربردهای مهم آن‌ها تجزیه عبارت‌های جبری است. همچنین، مطالبی را درباره اتحادهای مهم، از قبیل اتحاد مزدوج، اتحاد جمله مشترک، اتحاد چاق و لاغر و اتحاد مکعب بیان کردیم. در آموزش «اتحاد مربع چیست ؟ — اثبات، فرمول و نمونه سوال با جواب» نیز در این آموزش، مطالبی را درباره اتحاد مربع دو جمله ای بیان می‌کنیم و مثال‌هایی از آن را حل خواهیم کرد.

$$\large a ^ 2 - b ^ 2 = (a-b)(a+b)$$

اتحاد مربع دو جمله ای مجموع

اتحاد مربع دو جمله ای مجموع که به آن اتحاد نوع اول نیز می‌گویند، برای دو جمله عمومی $$a$$ و $$b$$ به‌صورت زیر بیان می‌شود: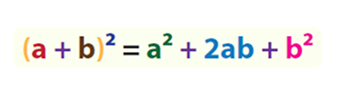

بنابراین، اتحاد مربع برای مجموع دو جمله این‌گونه بیان می‌شود: مربع مجموع دو جمله برابر است با مربع جمله اول به‌علاوه دو برابر حاصل‌ضرب دو جمله به‌علاوه مربع جمله دوم.

اثبات اتحاد مربع دو جمله ای مجموع

برای اثبات اتحاد مربع دو جمله ای مجموع کافی است که سمت چپ اتحاد، یعنی عبارتی را که به توان دو رسیده است، ساده کنیم و ببینیم که با طرف دیگر اتحاد برابر است. بنابراین، می‌نویسیم:

$$\large \begin{aligned} ( a + b ) ^ 2 & = ( a + b ) ( a + b ) \\ & = a ( a + b ) + b ( a + b ) \\ & = a ^ 2 + a b + b a +b ^ 2 \\ & = a ^ 2 + 2 a b + b ^ 2 \end{aligned}$$

مشاهده می‌کنیم که طرف اول و دوم اتحاد با هم مساوی هستند و بنابراین، اثبات کامل می‌شود.

اثبات اتحاد مربع دو جمله ای مجموع با شکل

برای اثبات اتحاد مربع دو جمله ای مجموع با شکل، مربعی به ضلع $$( a + b )$$ را در نظر می‌گیریم. به تقسیم‌بندی این مربع در شکل زیر دقت کنید.

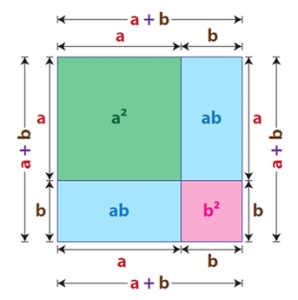
می‌دانیم که مساحت مربع با به توان دو رساندن اندازه ضلع آن محاسبه می‌شود. بنابراین، برای مربع شکل بالا خواهیم داشت:

$$\large ( a + b ) ^ 2$$

اکنون به روش دیگری نیز مساحت این مربع را محاسبه می‌کنیم. می‌بینیم که مربع بزرگ، خود از چهار شکل کوچک‌تر تشکیل شده است:‌

• مربعی به ضلع $$a$$
• مستطیلی به عرض $$b$$ و طول $$a$$
• مربعی به ضلع $$b$$
• مستطیلی به عرض $$b$$ و طول $$a$$

مجموع مساحت‌های این چهار شکل، برابر است با

$$\large a ^ 2 + a b + ab + b ^ 2 = a ^ 2 + 2 a b + b ^ 2$$

از آنجا که مساحت مربع بزرگ برابر با مساحت این چهار شکل است، می‌توان نوشت:‌

$$( a + b ) ^ 2 = a ^ 2 + 2 a b + b ^ 2$$

اتحاد مربع دو جمله ای تفاضل

اتحاد مربع برای تفاضل دو جمله $$a$$ و $$b$$ به‌صورت زیر بیان می‌شود:

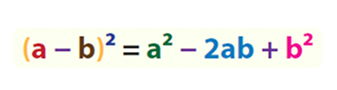
بنابراین، اتحاد مربع برای تفاضل دو جمله این‌گونه بیان می‌شود: مربع تفاضل دو جمله برابر است با مربع جمله اول منهای دو برابر حاصل‌ضرب دو جمله به‌علاوه مربع جمله دوم.

اثبات اتحاد مربع دو جمله ای‌ تفاضل

برای اثبات اتحاد مربع تفاضل دو جمله، مشابه اثبات اتحاد مربع مجموع دو جمله عمل می‌کنیم. بنابراین، کافی است که سمت چپ اتحاد، یعنی عبارتی را که به توان دو رسیده است، ساده کنیم و ببینیم که با طرف دیگر اتحاد برابر است. بنابراین، می‌نویسیم:

$$\large \begin{aligned} ( a - b ) ^ 2 & = ( a - b ) ( a - b ) \\ & = a ( a - b ) - b ( a - b ) \\ & = a ^ 2 - a b - b a +b ^ 2 \\ & = a ^ 2 - 2 a b + b ^ 2 \end{aligned}$$

مشاهده می‌کنیم که طرف اول و دوم اتحاد با هم مساوی هستند و بنابراین، اثبات کامل می‌شود.

فیلم آموزش ریاضی – پایه دهم | رشته های تجربی و ریاضی + گواهینامه در فرادرس

کلیک کنید

اثبات اتحاد مربع دو جمله ای‌ تفاضل با شکل

یک راه دیگر اثبات اتحاد مربع تفاضل دو جمله، استفاده از شکل است. برای اثبات اتحاد مربع با شکل، فرض کنید مربعی به ضلع $$a$$ داریم که هر ضلع آن را به دو بخش $$b$$ و $$a - b$$ تقسیم کرده‌ایم. این مربع در شکل زیر نشان داده شده است.

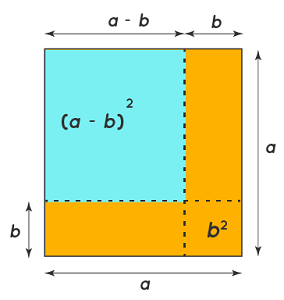
همان‌طور که می‌دانیم، مساحت یک مربع با به توان دو رساندن اندازه ضلع آن به‌دست می‌آید که برای این مربع برابر است با

$$\large a ^ 2$$

اما، همان‌طور که مشاهده می‌کنیم، مساحت این مربع خود از چهار مساحت تشکیل شده است:‌

• مربعی به ضلع $$a-b$$
• مستطیلی به عرض $$b$$ و طول $$a-b$$
• مربعی به ضلع $$b$$
• مستطیلی به عرض $$b$$ و طول $$a-b$$

بنابراین، خواهیم داشت:

$$\large \begin {align*} (a-b) ^ 2 + (a-b) b + (a-b)b + b ^ 2 & = a ^ 2 \\ (a-b)^2 +ab - b^2+ab - b ^ 2 + b^ 2 &= a ^ 2 \\ (a -b ) ^ 2 + 2 a b - b ^ 2 = a ^ 2 \\ ( a - b ) ^ 2 = a ^ 2 - 2 a b + b ^ 2 \end {align*}$$

می‌بینیم که طرف اول و دوم اتحاد با هم برابرند و بنابراین، اثبات کامل می‌شود.

مثال‌های اتحاد مربع دو جمله ای‌

در این بخش، مثال‌هایی را از اتحاد مربع دو جمله ای بیان می‌کنیم.

مثال اول اتحاد مربع دو جمله ای‌

فرض کنید $$x$$ یک عدد حقیقی است و در معادله $${ x } ^ { 2 } - 6 x + 5 = 0$$ صدق می‌کند. مقدار $$( x - 3 ) ^ 2$$ را به‌دست آورید.

حل: برای محاسبه عبارت، ابتدا معادله را به‌شکل اتحاد مربع دوجمله‌ای بازنویسی می‌کنیم. بدین منظور، عدد $$4$$ را به دو طرف معادله اضافه کنیم. چون به هر دو طرف معادله عدد $$4$$ را افزوده‌ایم، تغییری در جواب آن حاصل نمی‌شود.

بنابراین، داریم:

$$\large \begin {align} (r^ 2 - 6 r + 5 )+ 4 & = 0 + 4 \\ r ^ 2 - 6 r + 9 & = 4 \\ ( r - 3 ) ^ 2 & = 4 \\ \end {align}$$

در نتیجه، مقدار عبارت مورد نظر برابر با $$4$$ است.

فیلم روش تشخیص اتحادهای جمله مشترک، مزدوج، مربع دوجمله‌ای و سه جمله‌ای + مثال (آموزش رایگان) در فرادرس

کلیک کنید

مثال دوم اتحاد مربع دو جمله ای‌

مقدار عددی $$6 ^ 4$$ را به‌دست آورید.

حل: این عبارت را به‌صورت زیر می‌نویسیم:‌

$$\large 6 ^ 4 = (( 3 + 3 ) ^ 2 ) ^ 2$$

در واقع عبارت بالا یک سمت اتحاد مربع دوجمله‌ای است، که در آن، $$a = 3$$ و $$b = 3$$:

$$\large (( a + b ) ^ 2 ) ^ 2$$

با استفاده از اتحاد مربع دوجمله‌ای، می‌توان نوشت:

$$\large ( 3+ 3) ^2 = 3 ^ 2 + 2 ( 3 ) ( 3 ) + 3 ^ 2 = 36$$

بنابراین، داریم:

$$\large 6 ^ 4 = 36 ^ 2$$

باز هم می‌توانیم از اتحاد مربع دوجمله‌ای استفاده کنیم:

$$\large \begin {align} 36 ^ 2 & = ( 30 + 6 ) ^ 2 = 3 0^ 2 + 2 ( 30 ) ( 6 ) + 6 ^ 2 \\ & = 900+ 360+ 36 \\ & = 1296 \end {align}$$

بنابراین، جواب این مثال $$1296$$ است.

مثال سوم اتحاد مربع دو جمله ای‌

با استفاده از اتحاد مربع دو جمله ای مجموع و تفاضل، تساوی زیر را اثبات کنید.

$$\large ( x - y ) ^ 2 + ( x + y ) ^ 2 = 2 ( x ^ 2 + y ^ 2 )$$

حل: از دو اتحاد زیر استفاده می‌کنیم:

$$\large ( x - y ) ^ 2 = x ^ 2 - 2 x y + y ^ 2$$

$$\large ( x + y ) ^ 2 = x ^ 2 + 2 x y + y ^ 2$$

در نتیجه، می‌توان نوشت:

$$ \large \require {cancel} \begin {align*} ( x - y ) ^ 2 + ( x+ y ) ^ 2 & = x ^ 2 \cancel {- 2 x y} + y ^ 2 + x ^ 2 + \cancel { 2 x y } + y ^ 2\\ & = 2 x ^ 2 + 2 y ^ 2 = 2 ( x ^ 2 + y ^ 2 ) \end {align*} $$

مثال چهارم اتحاد مربع دو جمله ای

مقدار عبارت عددی زیر را إه‌دست آورید:

$$\large 73 ^ 2 + 2 \times 27 \times 73 + 27 ^ 2$$

حل: فرض می‌کنیم $$a = 73$$ و $$b = 27$$ باشد. در این‌‌صورت، می‌توانیم بنویسیم:

$$\large a ^ 2 + 2 \times b \times a + b ^ 2 = ( a + b) ^ 2 = 100 ^ 2 = 10000$$

مثال پنجم اتحاد مربع دو جمله ای‌

عبارت جبری زیر را تجزیه کنید.

$$\large p ^ 4 + 4$$

حل: باید این عبارت را به مربع کامل تبدیل کنیم. بدین منظور، جمله $$4 n ^ 2$$ را به عبارت اضافه و از آن کم می‌کنیم. بنابراین، خواهیم داشت:

$$\large p ^ 4 + 4 p ^ 2 + 4 - 4 p ^ 2 = ( p ^ 2 + 2 ) ^ 2 - 4 p ^ 2$$

اکنون از اتحاد مزدوج استفاده می‌کنیم و می‌نویسیم:

$$\large ( p ^ 2 + 2 ) ^ 2 - 4 p ^ 2 = ( p ^ 2 + 2 ) ^ 2 - ( 2 p ) ^ 2 = ( p ^ 2 + 2 + 2 p ) ( p ^ 2 + 2 - 2 p )$$

مثال ششم اتحاد مربع دو جمله ای‌

معادله زیر را در نظر بگیرید:

$$\large { a ^ 2 + b ^ 2 + c ^2 + d ^ 2 = a b + b c + c d + d a }$$

آیا اعداد حقیقی و متمایز $$a$$ و $$b$$ و $$c$$ و $$d$$ وجود دارند که در معادله بالا صدق کنند؟

حل: ابتدا، عدد $$2$$ را در این معادله ضرب می‌کنیم، سپس سمت راست آن را به سمت چپ می‌آوریم:

$$\large 2 ( a ^ 2 + b ^ 2 + c ^ 2 + d ^ 2 ) - 2 ( a b + b c + c d + d a ) = 0$$

جملات را به‌صورت زیر در کنار هم قرار می‌دهیم:

$$\large ( a ^ 2 - 2 a b + b ^ 2 ) + ( b ^ 2 - 2 b c + c ^ 2 ) + ( c ^ 2 - 2 c d + d ^ 2 ) + ( d ^ 2 - 2 d a + a ^ 2 ) = 0$$

اکنون از اتحاد مربع دو جمله ای استفاده می‌کنیم و تساوی زیر را خواهیم داشت:

$$\large ( a - b ) ^ 2 + ( b - c ) ^ 2 + ( c - d ) ^ 2 + ( d - a ) ^ 2 = 0$$

همان‌طور که می‌بینیم، طرف چپ تساوی مجموع چهار مربع کامل است. مربع کامل نیز تنها می‌تواند مثبت یا صفر باشد. بنابراین، برای آنکه تساوی برقرار باشد، باید چهار مربع کامل برابر با صفر باشند:

$$\large ( a - b ) ^ 2 = ( b - c ) ^ 2 = ( c - d ) ^ 2 = ( d - a ) ^ 2 = 0$$

در نتیجه، باید داشته باشیم:

$$\large a − b = b − c = c − d = d − a = 0$$

این یعنی اینکه $$a = b = c = d$$ که متناقض با مجزا بودن $$a$$ و $$b$$ و $$c$$ و $$d$$ است. در نتیجه، پاسخ به سؤال، خیر است.

مثال هفتم اتحاد مربع دو جمله ای‌‌

اگر $$x + \frac 1 x = 5$$ باشد، آنگاه مقدار عبارت $$x ^ 4 + \frac {1} { x ^ 4 }$$ را به‌دست آورید.

حل: اتحاد مربع دو جمله ای زیر را برای دو جمله $$x$$ و $$\frac 1 x$$ داریم:

$$\large ( x + \frac 1 x ) ^ 2 = x ^ 2 + 2 ( x ) ( \frac 1 x ) + (\frac 1 x ) ^ 2 = x ^ 2 +2 + \frac 1 { x ^ 2 } = x ^ 2 + \frac 1 { x ^ 2 } + 2$$

مقدار $$x + \frac 1 x = 5$$ را می‌دانیم و در تساوی بالا قرار می‌دهیم. بنابراین، خواهیم داشت:

$$\large ( 5) ^ 2 = 25 = x ^ 2 + \frac 1 { x ^ 2 } + 2$$

بنابراین، تساوی زیر را داریم:

$$\large x ^ 2 + \frac 1 { x ^ 2 } = 23$$

اکنون دو طرف تساوی بالا را به توان دو می‌رسانیم و می‌نویسیم:

$$\large \left ( x ^ 2 + \frac 1 { x ^ 2 } = 23 \right ) ^ 2 \Rightarrow \left ( x ^ 2 + \frac 1 { x ^ 2 } \right )^ 2 = 23 ^ 2$$

با به توان دو رساندن عبارت سمت چپ، می‌توان نوشت:

$$\large (x ^ 2)^ 2 + 2 ( x ^ 2 ) ( \frac 1 { x ^ 2 } ) + ( \frac 1 { x ^ 2 } ) ^ 2 = 529 \\ \large \Rightarrow x ^ 4 + 2 + \frac 1 { x ^ 4 } = 529 \\ \large \Rightarrow x ^ 4 + \frac 1 { x ^ 4 } = 529 - 2 = 527$$

مثال هشتم اتحاد مربع دو جمله ای‌

تساوی‌های زیر داده شده‌اند:

$$\large \begin {aligned} a + b & = c + 6 \\ a b - a c & = b c - 1 \\ \end {aligned}$$

مقدار $$a ^ 2 + b ^ 2 + c ^ 2$$ را محاسبه کنید.

حل: با استفاده از مقادیری که داده شده، می‌توانیم بنویسیم:

$$\large \begin {array} {lll} a ^ 2 + b ^ 2 + c ^ 2 & ={ ( a + b + c ) } ^ 2 - 2 ( a b + b c + ac ) \\ & = { ( ( c +6 ) + c ) }^ 2 - 2 ( ( b c + a c - 1 ) + b c + a c ) \\ & = { ( 2 c + 6 ) } ^ 2 - 2 ( 2 b c + 2 a c - 1 ) \\ & = { ( 4 c ^ 2 + 2 4 c + 3 6 ) } - 2 ( 2 c (b + a ) - 1 ) \\ & = { ( 4 c ^ 2 + 2 4 c+ 3 6) } - 2 ( 2 c ( c + 6 ) - 1 ) \\ & = { ( 4 c ^ 2 + 2 4 c + 3 6 ) } - ( 4 c ^ 2+ 2 4 c - 2 ) \\ & = 36 - ( - 2 ) = 36 + 2 = 38 \end {array}$$

مثال نهم اتحاد مربع دو جمله ای‌

با استفاده از اتحاد مربع دوجمله‌ای، مقدار عددی $$110^ 2$$ را محاسبه کنید.

حل: این عدد را می‌توان با استفاده از اتحاد جمع دوجمله‌ای یا همان اتحاد مربع دو جمله ای به صورت زیر نوشت و محاسبه کرد:

$$\large \begin {align*} ( 110 ) ^ 2 & = ( 100 + 10 ) ^ 2 = 100 ^ 2 + 2 ( 100 ) ( 10 ) + 10^ 2 \\ & = 10000+2000+ 100 = 12100 \end {align*}$$

مثال دهم اتحاد مربع دو جمله ای‌

اگر $$x + y = 10$$ و $$x y = 5$$ باشد، حاصل $$x ^ 2 + y ^ 2$$ را به دست آورید.

حل: از اتحاد مربع دو جمله ای کمک می‌گیریم:

$$\large ( x + y ) ^ 2 = x ^2 + 2 x y + y ^ 2$$

طبق این رابطه، می‌توانیم تساوی زیر را بنویسیم:

$$\large x ^ 2 + y ^ 2 = ( x + y ) ^ 2 - 2 x y$$

بنابراین، مقدار مورد نظر این‌گونه به‌دست می‌آید:

$$\large x ^ 2 + y ^ 2 = ( 10) ^ 2 - 2 ( 5 ) = 100 -10 = 90$$

جمع‌بندی

در این مطلب از مجله فرادرس، با اتحاد مربع دو جمله ای آشنا شدیم. همچنین، اثبات آن را به دو روش بیان کردیم. در پایان نیز مثال‌های متنوعی را از کاربرد این اتحاد حل کردیم.