رگرسیون خطی چندگانه (Multiple Linear Regression) – به زبان ساده

یکی از روش‌های مرسوم در تحلیل چند متغیره، تکنیک «رگرسیون خطی چندگانه» (Multiple Linear Regression) است. بر اساس تحلیل رگرسیونی، یک رابطه خطی بین «متغیر پاسخ» (Response Variable) با یک یا چند «متغیر توصیفی» (Explanatory Variable) برقرار می‌شود. البته گاهی به متغیر پاسخ، «متغیر وابسته» (Dependent Variable) و به متغیرهای توصیفی، «متغیرهای مستقل» (Independent Variables) نیز می‌گویند.

اگر رابطه خطی بین یک متغیر پاسخ و یک متغیر مستقل برقرار شود، تکنیک رگرسیون را رگرسیون خطی ساده (Simple Linear Regression) می‌نامند. ولی در صورت به کارگیری چندین متغیر توصیفی یا مستقل در مدل رگرسیونی، روش رگرسیونی را «چند گانه» (Multiple Linear Regression) می‌گویند. البته روش رگرسیونی دیگری براساس چند متغیر پاسخ و مستقل نیز به کار گرفته می‌شود که به آن «رگرسیون چند متغیره» (Multivariate Regression) گفته شده و بیش از یک متغیر پاسخ مورد تحلیل و مدل‌سازی قرار می‌گیرد.

از رگرسیون خطی چندگانه در بسیاری از شاخه‌های علوم بخصوص فیزیک و شیمی استفاده می‌شود. همچنین برای پیشگویی روند داده‌های مالی از رگرسیون چندگانه بهره می‌گیرند.

البته در این نوشتار به بررسی رگرسیون چندگانه می‌پردازیم. برای اطلاع از مبانی و تاریخچه رگرسیون بهتر است مطلب رگرسیون خطی — مفهوم و محاسبات به زبان ساده را بخوانید. همچنین خواندن نوشتار ضریب‌های همبستگی (Correlation Coefficients) و شیوه‌ محاسبه آن‌ها — به زبان ساده و هم خطی در مدل رگرسیونی — به زبان ساده نیز خالی از لطف نیست.

رگرسیون خطی چندگانه (Multiple Linear Regression)

در رگرسیون خطی چندگانه، پارامترهای یک مدل خطی به کمک یه تابع هدف و مقدارهای متغیرها، برآورد می‌شوند. در رگرسیون خطی، مدل در نظر گرفته شده، یک رابطه خطی برحسب پارامترهای مدل است.

به این ترتیب اگر $$n$$ مشاهده از متغیر مستقل $$p$$ بعدی $$X$$ داشته باشیم و بخواهیم یک رابطه خطی با متغیر پاسخ $$y$$ برقرار کنیم، می‌توانیم از مدل رگرسیون خطی زیر استفاده کنیم.

$$\large y_{i}=\beta _{0}1+\beta _{1}x_{i1}+\cdots +\beta _{p}x_{ip}+\varepsilon _{i},\qquad i=1,\ldots ,n$$

از آنجایی که متغیر مستقل $$X$$ دارای $$p$$ بعد است، مقدار آن را در هر بعد با یک متغیر مستقل یک بعدی جایگزین کرده‌ایم. مشخص است که اندیس $$i$$ نیز شماره مشاهده را نشان می‌دهد. در انتها نیز $$\varepsilon$$ جمله خطای مدل رگرسیونی محسوب می‌شود.

نکته: باید توجه داشت که در مدل رگرسیون خطی، رابطه بین پارامترها خطی است. به این ترتیب مدلی به صورت $$y=\beta_0+\beta_1x_1+\beta_2x^2_2+\epsilon$$ نیز یک مدل خطی برحسب پارامترها است. در حالیکه رابطه $$y=\beta_0+x_1^{\beta_1}+\beta^2_2x^2_2+\epsilon$$ دیگر یک رابطه خطی براساس پارامترها محسوب نخواهد شد.

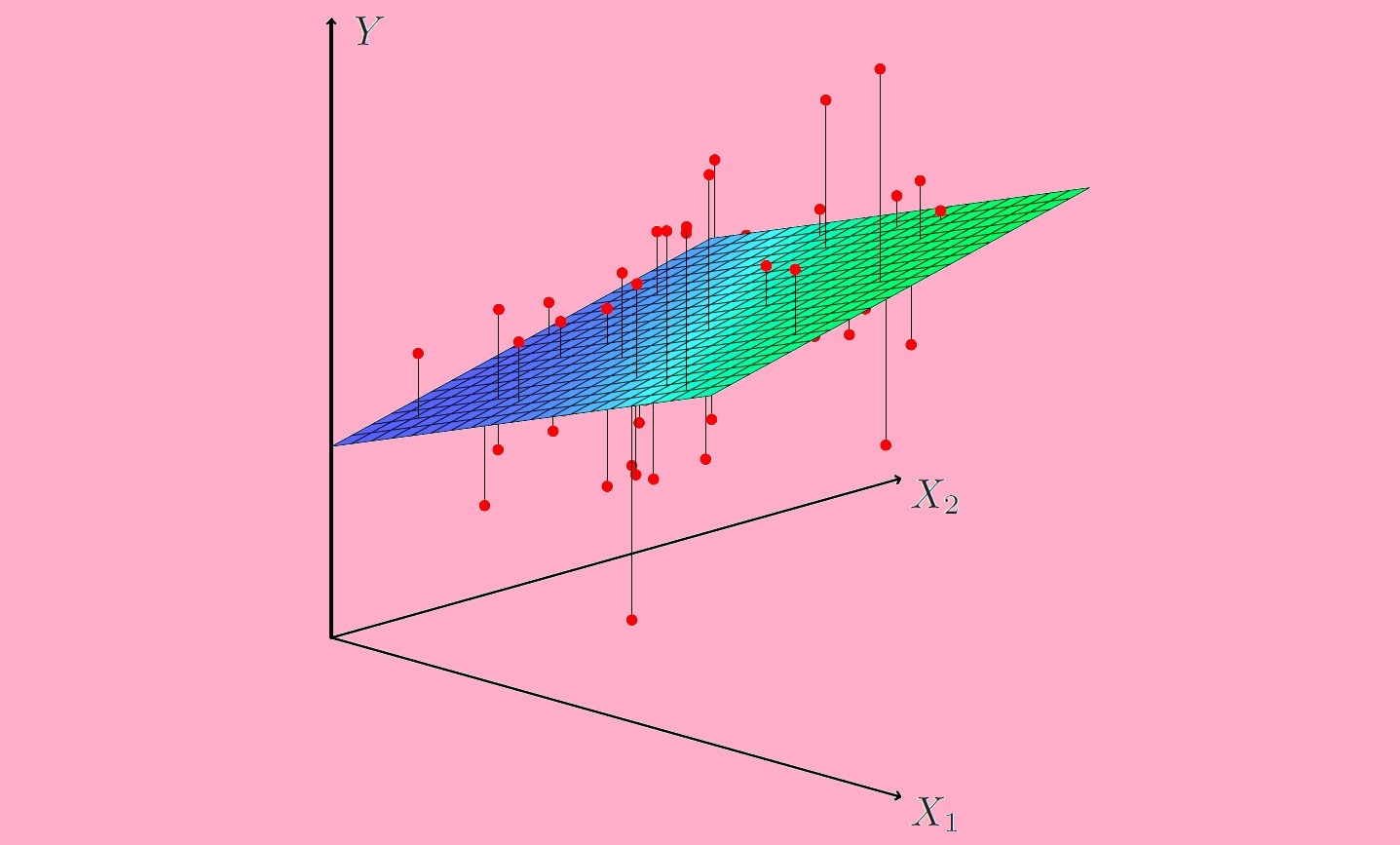
در رگرسیون خطی ساده، رابطه بین متغیر مستقل و وابسته به صورت معادله یک خط بیان می‌شود. در رگرسیون چندگانه، اگر دو متغیر مستقل با یک متغیر وابسته در رابطه خطی باشند، شکل این رابطه به صورت یک صفحه (plane) در خواهد آمد. در صورتی که بیش از دو متغیر مستقل در مدل رگرسیون خطی به کار روند، مدل به شکل یک «ابرصفحه» (Hyperplane) ظاهر می‌شود.

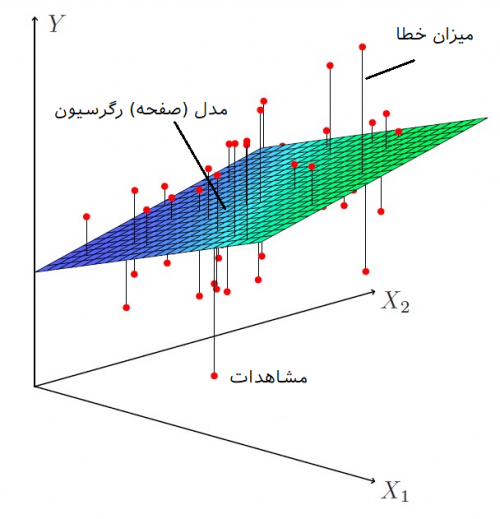
مدل رگرسیون خطی

مدل رگرسیون خطی را می‌توان به صورت یک رابطه برداری نیز نوشت.

$$\large \mathbf{y}_i= \mathbf {x}_{i}^{\mathsf {T}}{\mathbf{\beta }}+\varepsilon _{i},\qquad i=1,\ldots ,n$$

در این حالت، $$x_{i}^T$$، یک بردار است که دارای $$p$$ ستون است. همچنین $$\beta$$ نیز برداری است که $$p$$ سطر دارد. ضمناً منظور از $$\mathbf {x}_{i}^{\mathsf {T}}{\mathbf{\beta }}$$‌ نیز ضرب داخلی این دو بردار است که حاصل آن یک عدد (Scalar) خواهد بود. اگر بردارهای $$x_i$$ و $$\beta$$ مشخص باشند می‌توان مقدار متغیر پاسخ یعنی $$y_i$$ را با میزان خطای متوسط $$\epsilon$$، بر اساس هر مشاهده برآورد کرد.

این محاسبات را به صورت ماتریسی و برای همه مشاهدات به صورت یکجا نیز نوشته‌اند. فرض کنید که $$y$$ بردار مشاهدات متغیر پاسخ باشد. به همین ترتیب $$X$$ نیز ماتریس مربوط به متغیر مستقل $$p$$ بعدی و $$\beta$$ نیز بردار پارامترهای مدل با $$p$$ سطر باشد. اگر بردار خطا را نیز $$\epsilon$$ بنامیم، مدل رگرسیون خطی را می‌توان به زبان ماتریس و بردارها به صورت زیر بازنویسی کرد.

$$\large y=X\beta+\epsilon$$

ماتریس‌ها و بردارها به کار رفته در رابطه بالا در ادامه قابل مشاهده‌اند.

$$\large \mathbf {y} ={\begin{pmatrix}y_{1}\\y_{2}\\\vdots \\y_{n}\end{pmatrix}}_{n\times 1},\quad {\displaystyle X={\begin{pmatrix}\mathbf {x} _{1}^{\mathsf {T}}\\\mathbf {x} _{2}^{\mathsf {T}}\\\vdots \\\mathbf {x} _{n}^{\mathsf {T}}\end{pmatrix}}_{n\times (p+1)}={\begin{pmatrix}1&x_{11}&\cdots &x_{1p}\\1&x_{21}&\cdots &x_{2p}\\\vdots &\vdots &\ddots &\vdots \\1&x_{n1}&\cdots &x_{np}\end{pmatrix}}_{n \times (p+1)}} \\\large {\displaystyle {\boldsymbol {\beta }}={\begin{pmatrix}\beta _{0}\\\beta _{1}\\\beta _{2}\\\vdots \\\beta _{p}\end{pmatrix}}_{(p+1)\times 1},\quad {\boldsymbol {\varepsilon }}={\begin{pmatrix}\varepsilon _{1}\\\varepsilon _{2}\\\vdots \\\varepsilon _{n}\end{pmatrix}}}_{n\times 1}$$

در ادامه به بررسی ماتریس‌ و بردار مورد استفاده در رابطه بالا خواهیم پرداخت.

بردار مشاهدات متغیر پاسخ ($$y$$): این بردار از مقدارهای متغیر پاسخ برای هر مشاهده یعنی $$y_i$$ ها تشکیل شده است. به این ترتیب $$y_1$$ مقدار متغیر پاسخ برای مشاهده اول و $$y_i$$ مقدار متغیر پاسخ برای مشاهده iام و در انتها نیز $$y_n$$ نیز مقدار متغیر پاسخ برای مشاهده nام است. پس $$y$$ یک بردار n سطری است.

ماتریس متغیر‌های مستقل ($$X$$): سطرهای این ماتریس، از مقدار مشاهدات متغیرهای مستقل تشکیل شده است. به این ترتیب سطر اول مربوط به مقدارهای متغیرهای مستقل برای مشاهده اول است. از آنجایی که هر مشاهده دارای $$p$$ متغیر مستقل است، تعداد ستون‌های این ماتریس نیز $$p+1$$ است. از طرفی با توجه به $$n$$ مشاهده نیز مشخص است که تعداد سطرهای این ماتریس باید برابر با $$n$$ باشد. پس این ابعاد این ماتریس را می‌توان به صورت $$(p+1)\times n$$ در نظر گرفت.

نکته: همانطور که در ماتریس $$X$$ مشاهده می‌کنید، همه مقادیر مربوط به ستون اول برابر با ۱ هستند. در نتیجه این ماتریس دارای $$n$$ سطر و $$p+1$$ ستون است. این امر به علت آن است که برای مقدار ثابت در بردار $$\beta$$ (یعنی مقدار $$\beta_0$$) نیز امکان محاسبه وجود داشته باشد. اگر در مدل رگرسیون مقدار ثابت در نظر گرفته نشود، این ستون را حذف کرده و در بردار پارامترها نیز $$\beta_0$$ را در نظر نمی‌گیرند. گاهی به ماتریس $$X$$، «ماتریس طرح» (Design Matrix) نیز می‌گویند.

بردار پارامترها ($$\beta$$): این بردار در حالت عمومی دارای $$p+1$$ سطر است که $$\beta_0$$ مقدار ثابت در مدل را نشان می‌دهد. این پارامترهای در صورت برآورد، همان «ضرایب مدل رگرسیونی» (Regression Coefficients) هستند. مقدار این ضرایب، حساسیت متغیر پاسخ را به هر یک از متغیرهای مستقل نشان می‌دهد. محاسبه این ضرایب به کمک کمینه سازی «مجموع مربعات خطا» (Ordinary Least Square) و براساس محاسبه «مشتقات جزئی» (partial deviation) صورت می‌گیرد. اگر مقدار ثابت ($$\beta_0$$) در مدل رگرسیون لحاظ نشود، این بردار دارای $$p$$ سطر خواهد بود. البته باید توجه داشت که در این حالت، ماتریس $$X$$ نیز دچار تغییر خواهد شد. به متن مربوط به نکته بالا توجه کنید.

بردار خطا ($$\epsilon$$): این بخش از مدل رگرسیون خطی، «جمله خطا» (Error Term) نامیده می‌شود. مقدار این عبارت شامل همه عواملی است که ممکن است روی مقدار متغیر پاسخ تاثیر گذار بوده ولی در مدل رگرسیونی منظور نشده‌اند. این بردار به تعداد مشاهدات سطر دارد. به این ترتیب بُعد آن به صورت $$n \times 1$$ است.

مثال

در فیزیک و قوانین حرکت خوانده‌ایم که مسافت طی شده از مکان $$h_0$$ در طی زمان $$t$$ برای یک جسم با شتاب $$a$$ و سرعت اولیه $$v_0$$ به صورت زیر نوشته می‌شود.

$$\large h(t)=h_0+v_0\;t+\frac{1}{2}a\;t^2+\varepsilon(t)$$

واضح است که در این مدل یک رابطه رگرسیون خطی وجود دارد. با استفاده از داده‌های اندازه‌گیری شده برای حرکت یک جسم با شتاب، سرعت اولیه و زمان‌های مختلف، امکان برآورد این پارامترها بوجود می‌آید. حال می‌توان مشاهدات برای چنین مدلی را به صورت زیر نشان داد.

$$\large h_{i}=\beta_0+\beta _{1}t_{i}+\beta _{2}t_{i}^{2}+\varepsilon _{i}$$

در اینجا مشخص است که یک مدل رگرسیون دوگانه مورد نظر است. متغیرهای توصیفی در این مدل به ترتیب $$t$$ و $$t^2$$ هستند و هر مشاهده به  صورت $$X_i=(x_{i1},x_{i2})$$ متناظر با $$(t_i,t^2_i)$$ نوشته می‌شوند. این مدل برحسب متغیر زمان، غیر خطی ولی براساس پارامترها یک مدل خطی محسوب می‌شود. به این ترتیب $$\beta_1=v_0$$ و $$\beta_2=\frac{1}{2}a$$ خواهند بود. $$\beta_0$$ نیز تغییر مکان در زمان صفر است. (البته می‌توان در چنین مدلی مقدار $$\beta_0$$ را صفر در نظر گرفت زیرا در زمان صفر هیچ تغییر مکانی وجود ندارد.

برآورد پارامترهای مدل رگرسیون خطی

مدل برداری و ماتریسی رگرسیون خطی را در نظر بگیرید. همانطور که بیان کردیم، یکی از روش‌های برآورد پارامترهای این مدل استفاده از تکنیک OLS یا «کمینه سازی مربعات خطا» (Ordinary Least Square) است. در این قسمت به بررسی این روش به منظور برآورد پارامترهای مدل رگرسیون خطی می‌پردازیم.

فیلم آموزش تحلیل رگرسیون لجستیک دو حالتی در SPSS اس پی اس اس در فرادرس

کلیک کنید

اگر $$S(\beta)$$ را به صورت زیر معرفی کنیم، هدف از برآورد پارامترهای مدل رگرسیون خطی، محاسبه بردار $$\beta$$ برحسب مقدار مشاهدات است تا $$S(\beta)$$ حداقل ممکن شود.

$$\large {\displaystyle S({\boldsymbol {\beta }})=\sum _{i=1}^{n}{\bigl |}y_{i}-\sum _{j=1}^{p}X_{ij}\beta _{j}{\bigr |}^{2}={\bigl \|}\mathbf {y} -\mathbf {X} {\boldsymbol {\beta }}{\bigr \|}^{2}}$$

مشخص است که منظور از $${\bigl \|}\mathbf {y} -\mathbf {X} {\boldsymbol {\beta }}{\bigr \|}^{2}$$ مربع فاصله یا نرم اقلیدسی است. اگر برآورد بردار پارامترها را با $$\widehat{\beta}$$ نشان دهیم، پارامترهای مدل، مقادیری هستند که در رابطه زیر صدق کنند.

$$\large {\widehat {\boldsymbol {\beta }}}={\underset {\boldsymbol {\beta }}{\operatorname {arg\,min} }}\,S({\boldsymbol {\beta }})$$

به کمک مشتق‌گیری و حل معادلات ماتریسی، برآورد پارامترها به صورت زیر خواهد بود.

$$\large {\displaystyle {\widehat {\boldsymbol {\beta }}}=(\mathbf {X} ^{\rm {T}}\mathbf {X} )^{-1}\mathbf {X} ^{\rm {T}}\mathbf {y}}$$

توجه داشته باشید که این برآورد، زمانی امکان پذیر است که ماتریس $$(X^TX)^{-1}$$ معکوس پذیر باشد. به این معنی که دترمینان آن باید مخالف صفر بوده تا نشان دهنده عدم وابستگی خطی بین سطرها یا ستون‌های ماتریس باشد. به همین دلیل یکی از شرط‌های اصلی در مدل رگرسیون خطی، استقلال متغیرهای توصیفی است. در غیر این صورت ماتریس $$(X^TX)^{-1}$$ معکوس پذیر نبوده و امکان برآورد پارامترها وجود ندارد. همچنین وجود شرط کم بودن تعداد متغیرها نسبت به مشاهدات ($$p<$$) نیز به این منظور باید رعایت شود. در نوشتار رگرسیون لاسو (Lasso Regression) — به زبان ساده، مثالی وجود دارد که با توجه به بزرگ بودن بعد مسئله نسبت به مشاهدات، معکوس‌پذیری ماتریس $$(X^TX)$$ از بین می‌رود.

توجه داشته باشید اگر فقط یک متغیر مستقل وجود داشته باشد، مدل رگرسیونی به صورت مدل رگرسیونی خطی ساده در خواهد آمد. برآورد پارامترهای چنین مدلی به سادگی به کمک مشتق از تابع مربعات خطا و حل یک دستگاه حاصل می‌شود. به این ترتیب $$\beta_0$$ «عرض از مبدا» (Intercept) و $$\beta_1$$ نیز «شیب خط» (Coefficient) را نشان می‌دهند.

نکته: اگر تعداد پارامترها بیشتر از تعداد مشاهدات باشد باید از روش‌های رگرسیون دیگر مانند رگرسیون لاسو (Lasso Regression) استفاده کرد.

فرضیات مدل رگرسیون خطی در تکنیک OLS

در برآورد پارامترهای مدل رگرسیون خطی به روش OLS باید شرط‌هایی را در نظر گرفت تا مدل ارائه شده، معتبر باشد. در ادامه این شرط‌ها مورد بررسی قرار می‌گیرند.

مدل توصیفی

در هنگام ایجاد مدل رگرسیونی باید متغیرهایی مستقلی که بیشترین میزان رابطه را با متغیر پاسخ دارند به کار گرفت. همچنین به منظور بررسی رابطه خطی بین متغیرهای پاسخ و مستقل از ضرایب همبستگی یا ترسیم نقاط در حالت سه بعدی (یا حتی زوج‌های متغیرهای مستقل و پاسخ) کار ساز است.

عدم وابستگی متغیرهای مستقل با جمله خطا

جملات خطا نباید هیچ وابستگی با متغیرهای مستقل داشته باشند، از طرفی میانگین جملات خطا نیز باید صفر باشد. به این ترتیب باید شرط $$E(\varepsilon)=0$$ و همچنین $$E(\varepsilon|X)=0$$ بررسی و مورد تایید قرار گیرد تا مدل حاصل از OLS در رگرسیون خطی معتبر باشد. توجه دارید که منظور از $$E(\varepsilon)$$ امید ریاضی (میانگین) جملات خطا است.

فیلم آموزش رگرسیون خطی ساده (رایگان) در فرادرس

کلیک کنید

عدم وابستگی خطی

همانطور که دیدیم، یکی از شرط‌ها در محاسبات OLS، معکوس پذیر بودن ماتریس $$X^TX$$ بود. به این ترتیب ماتریس $$X$$ باید پر رتبه باشد. به بیان دیگر باید رابطه زیر برای این ماتریس برقرار باشد.

$$\large \Pr \!{\big [}\,\operatorname {rank} (X)=p\,{\big ]}=1$$

این شرط بوسیله عدم وابستگی خطی بین متغیرهای مستقل تضمین می‌شود. به این ترتیب قبل از اجرا و انجام محاسبات رگرسیون خطی باید وجود رابطه خطی بین متغیرهای مستقل بوسیله ضریب همبستگی یا رسم نمودارهای نقطه‌ای (Scatter Plot) مورد تایید قرار گیرد. در صورت وابستگی خطی بین متغیرهای توصیفی با مشکل «هم‌خطی چندگانه» (Multicollinear) مواجه خواهیم شد و مقدار هر متغیر در پارامترهای متغیرهای دیگر تاثیر گذار خواهد بود. در این صورت واریانس براوردگرها بزرگ شده و اعتبار مدل از بین خواهد رفت.

خصوصیات جملات خطا

به منظور اعتبار بخشی و همچنین بررسی فرضیات برآوردهای صورت گرفته توسط روش OLS باید شرایط زیر را برای جملات خطا مورد کاوش قرار دارد.

ثابت بودن واریانس: واریانس جملات خطا باید ثابت باشد. به این معنی که با توجه به مشاهدات صورت گرفته، واریانس جمله خطا تغییر نکند. به بیان آماری این جمله را به صورت زیر بیان می‌کنیم.

$$\large E[ \varepsilon^2_i | X ] = \sigma^2$$

در صورتی که واریانس ثابت نباشد، با استفاده از وزن‌دهی به مشاهدات می‌توان واریانس را ثابت کرد. این عمل در برآورد پارامترهای «رگرسیونی وزنی» (Weighted Least Squares) مورد استفاده قرار می‌گیرد.

عدم وابستگی جملات خطا: استقلال عبارت خطا برای مشاهدات یکی از فرضیات مهم در روش OLS محسوب می‌شود. با توجه به ثابت بودن واریانس عبارت خطا، عدم وابستگی بین جملات خطا را می‌توان به صورت زیر نشان داد.

$$\large E[ \varepsilon_i\varepsilon_j | X ] =0$$

توزیع نرمال برای جملات خطا: هر چند این شرط، مربوط به تکنیک OLS‌ نیست ولی گاهی اوقات برای امکان اجرای آزمون فرض در مورد پارامترهای برآورد شده این شرط ضروری به نظر می‌رسد. به این ترتیب توزیع احتمالی عبارت خطا به شرط متغیرهای مستقل باید نرمال باشد. با توجه به توضیحات گفته شده در این بخش، خواهیم داشت:

$$\large \varepsilon \mid X\sim {\mathcal {N}}(0,\sigma ^{2}I_{n})$$

در ادامه به بررسی مثالی می‌پردازیم که در آن بوسیله رگرسیون خطی، یک تابع غیرخطی مثل $$\sin(x)$$ را برآورد می‌کنیم.

تخمین تابع سینوس بوسیله رگرسیون خطی

همانطور که در مطلب سری تیلور — از صفر تا صد خوانده‌اید، می‌دانید که امکان تقریب زدن توابع مثلثاتی بوسیله چند جمله‌ای‌ها وجود دارد. بسط یا سری تیلور برای تابع سینوس به صورت زیر نوشته می‌شود.

$$\large \sin(x) = x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}+...$$

در اینجا هم با کمی اقماض در مورد وابستگی متغیرهای مستقل، سعی می‌کنیم به کمک داده‌های تولید شده بوسیله بسط یا سری تیلور و برآورد پارامترهای مدل رگرسیونی، تقریبی مناسب برای تابع سینوس ارائه دهیم. هر چه تعداد جملات سری تیلور بیشتر باشد دقت در محاسبه سینوس زاویه بیشتر می‌شود. در مدل رگرسیون خطی نیز اگر تعداد متغیرها را بیشتر در نظر بگیریم و از جملاتی بیشتر سری تیلور استفاده کنیم، دقت برآوردها بیشتر شده و به مقدار واقعی سینوس هر زاویه نزدیکتر می‌شویم.

مثال

جدول زیر مربوط به داده‌هایی است که براساس مقدار توان‌های فرد (یک، سه و پنچ) از زاویه‌های مختلف (برحسب رادیان) و همچنین مقدار سینوس آن زوایه‌ها ساخته شده است. قرار است، بوسیله مدل رگرسیون خطی، ضرایب مربوط به بسط یا سری تیلور را محاسبه کنیم تا با دقت مناسب مقدار سینوس هر زاویه را بدست آوریم. البته از آنجایی که سینوس هر زاویه از قبل مشخص است، می‌توانیم مقدار خطا را اندازه‌گیری کرده و نسبت به مناسب بودن مدل (کم بودن خطای مدل) تصمیم بگیریم.

از آنجایی که برای برآورد مقدار تابع سینوس از متغیرهای $$X$$ و $$X^3$$ استفاده خواهیم کرد، لازم است ابتدا ماتریس‌ $$X$$ و بردارهای $$\beta$$ و $$y$$ را تشکیل دهیم.

بردار $$y$$ بوسیله مقدارهای ستون $$y=sin(x)$$ ساخته می‌شود. پس داریم:

$$\large \mathbf {y} ={\begin{pmatrix}0\\0.2\\0.39\\0.56\\0.72\\0.84\end{pmatrix}}_{6\times 1}$$

حال به ایجاد ماتریس $$X$$ می‌پردازیم. توجه داشته باشید که در این مسئله از دو متغیر توصیفی برای پیش‌بینی مقدار سینوسن در بسط تیلور استفاده خواهیم کرد.

$$\large {\displaystyle X={\begin{pmatrix}\mathbf {x} _{1}^{\mathsf {T}}\\\mathbf {x} _{2}^{\mathsf {T}}\\\vdots \\\mathbf {x} _{n}^{\mathsf {T}}\end{pmatrix}}_{n\times p}={\begin{pmatrix}0&0\\0.2&0.008\\ 0.4&0.064\\ 0.6&0.216 \\ 0.8&0.512\\ 1&1\end{pmatrix}}_{6 \times 2}}$$

نکته: از آنجایی که در این مدل، مقدار ثابت وجود ندارد ماتریس $$X$$ دارای $$p=2$$ ستون خواهد بود. همین موضوع را در هنگام نوشتن بردار $$\beta$$ نیز رعایت می‌کنیم و برای آن فقط $$p=2$$ سطر در نظر می‌گیریم. به این ترتیب مقدار $$\beta_0=0$$ است.

با در نظر گرفتن این موضوع، بردار $$\beta$$ هم به شکل زیر نوشته می‌شود.

$$\large {\displaystyle {\boldsymbol {\beta }}={\begin{pmatrix}\beta _{1}\\\beta _{2}\end{pmatrix}}_{2\times 1}}$$

حال با استفاده از رابطه $$\widehat{\beta}=(X^TX)^{-1}X^Ty$$ برآورد پارامترها را محاسبه می‌کنیم. در گام اول بخش ابتدایی رابطه یعنی $$X^TX$$ را محاسبه می‌کنیم. به کمک روابطی که در جبر خطی برای پیدا کردن ترانهاده ماتریس‌ها و ضرب آن‌ها به یاد داریم، نتیجه این محاسبه به صورتی که در ادامه قابل مشاهده است در خواهد آمد.

$$\large X^TX=\begin{pmatrix}2.2&1.5664\\1.5664&1.31296\end{pmatrix}$$

در گام دوم به معکوس ماتریس بالا احتیاج داریم. به این ترتیب معکوس این ماتریس مطابق با رابطه زیر خواهد بود.

$$\large (X^TX)^{-1}=\begin{pmatrix}3.019&-3.6017\\-3.6017&5.0586\end{pmatrix}$$

در گام سوم نیز حاصل ضرب ماتریس $$X^T$$ در بردار مشاهدات متغیر پاسخ $$y$$ نیز به صورت زیر قابل محاسبه است.

$$\large X^Ty=\begin{pmatrix}0&0.2&0.4&0.6&0.8&1\\0&0.008&0.064&0.216&0.512&1 \end{pmatrix}\begin{pmatrix}0\\0.2\\0.39\\0.56\\0.72\\0.84\end{pmatrix} =\begin{pmatrix}1.948\\1.3562 \end{pmatrix}$$

در انتها، براساس ضرب این قسمت‌ها، برآورد پارامترهای مدل رگرسیون دو گانه، حاصل خواهد شد.

$$(X^TX)^{-1}X^Ty=\begin{pmatrix}0.9964\\-0.1559\end{pmatrix}$$

پس مشخص است که پارامتر اول برای این مدل رگرسیونی برابر $$\beta_1=0.9964$$ و پارامتر دوم نیز برابر با $$\beta_2=-0.1559$$ است.

نکته: همانطور که در سری یا بسط تیلور تابع سینوس دیده می‌شود ضرایب مربوط به هر یک از متغیرها به ترتیب به صورت $$1$$ و $$-\frac{1}{3!}=-0.166$$ است که با برآوردهای حاصل از رگرسیون بسیار نزدیک است.

اگر بوسیله مدل بدست آمده، خطا (مقدار تفاضل واقعی سینوس از برآورد مقدار سینوس توسط مدل رگرسیونی) را اندازه‌گیری کنیم، مجموع مربعات خطا، حداقل ممکن را نسبت به هر رابطه خطی دیگر خواهد داشت. به جدول زیر توجه کنید.

همانطور که دیده می‌شود، مجموع مربعات خطای این مدل بسیار به صفر نزدیک است که نشانگر مناسب بودن مدل است. سنجش فرض‌های مربوط به رگرسیون خطی برای چنین مدلی به علت کم بودن تعداد مشاهدات به درستی صورت نخواهد گرفت. البته به منظور ارزیابی مدل حاصل باید از روش‌های دیگری مانند آنالیز واریانس و آزمون فرض استفاده کرد که در این نوشتار از آن‌ها صرفنظر می‌کنیم. در دیگر نوشتارهای فرادرس با موضوع رگرسیون خطی با SPSS به بررسی و سنجش فرضیات مدل و ارزیابی آن خواهیم پرداخت.

اگر مطلب بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش های SPSS
• مجموعه آموزش‌های داده کاوی یا Data Mining در متلب
• مجموعه آموزش‌های نرم‌افزارهای آماری
• آموزش همبستگی و رگرسیون خطی در SPSS
• رگرسیون خطی — مفهوم و محاسبات به زبان ساده
• تحلیل واریانس (Anova) — مفاهیم و کاربردها

^^