فرادرسولتاژ متوسط — از صفر تا صد
در این مطلب قصد داریم به بررسی روش‌های محاسبه ولتاژ متوسط (Average Voltage) در یک شکل موج سینوسی بپردازیم. برای یافتن ولتاژ متوسط از هر دو روش گرافیکی و نیز روش عددی استفاده خواهیم کرد.
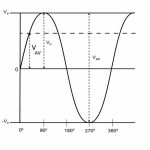
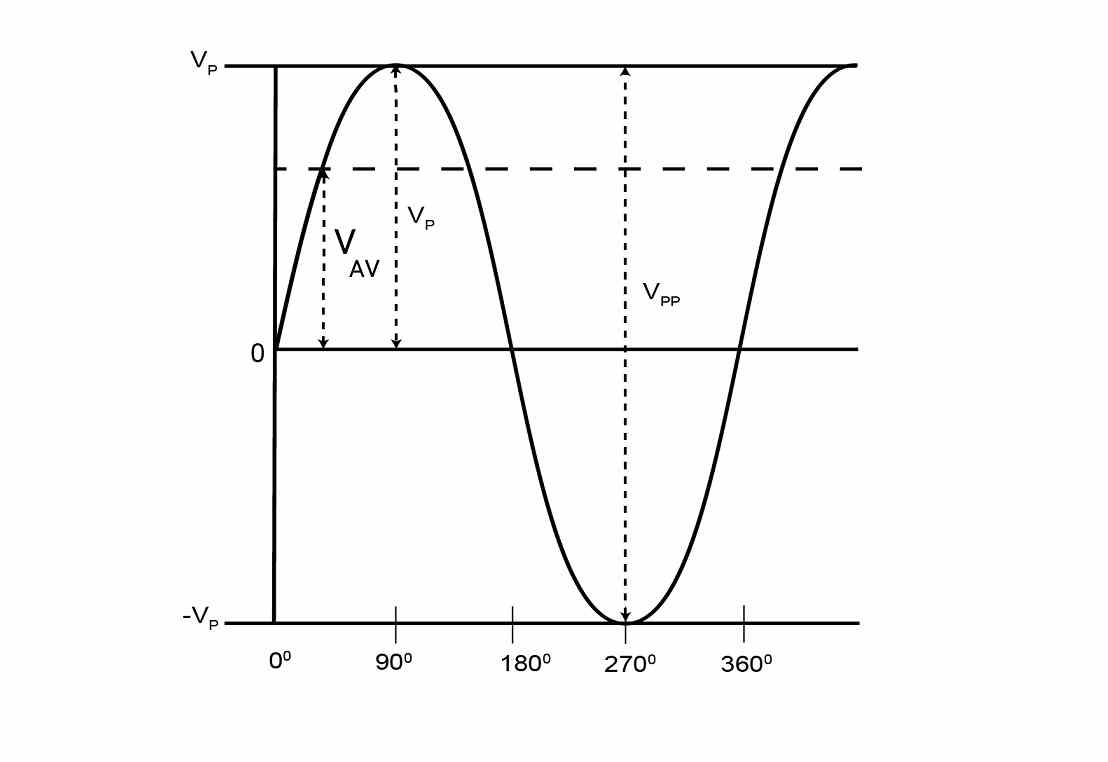
ولتاژ متوسط
فرایند یافتن ولتاژ متوسط یا میانگین مربوط به یک شکل موج متناوب بسیار شبیه به یافتن مقدار RMS سیگنال است که در مطالب قبلی مجله فرادرس به آن پرداخته شد. تنها تفاوتی که در محاسبه مقدار ولتاژ متوسط و ولتاژ RMS سیگنال وجود دارد این است که در محاسبه ولتاژ متوسط، مقادیر لحظه‌ای به توان دو نمی‌رسند و در واقع برای محاسبه ولتاژ متوسط از جذر مجموع مربعات سیگنال استفاده نمی‌شود.
مقدار جریان یا ولتاژ متوسط یک شکل موج متناوب سینوسی، مربعی یا مثلثی یا ... به صورت حاصل تقسیم ناحیه زیر آن شکل موج در یک دوره تناوب از سیگنال، تقسیم بر اندازه زمان محاسبه می‌شود. به عبارت دیگر، مقدار میانگین تمام ولتاژهای لحظه‌ای در راستای محور زمان در یک دوره تناوب کامل از سیگنال برابر با مقدار ولتاژ متوسط خواهد بود.
برای یک سیگنال متناوب، ناحیه بالای محور افقی عددی مثبت در نظر گرفته می‌شود، در حالی‌که ناحیه زیر محور افقی عددی منفی محسوب خواهد شد. در نتیجه مقدار متوسط یا میانگین یک سیگنال متناوب متقارن برابر با صفر به دست خواهد آمد؛ زیرا ناحیه بالای محور افقی در نیم‌سیکل مثبت برابر با ناحیه زیر محور افقی در نیم‌سیکل منفی است و به همین دلیل این دو مقدار مثبت و منفی همدیگر را خنثی می‌کنند و مقدار ولتاژ متوسط نهایی برابر با صفر به دست می‌آید.
بنابراین برای محاسبه مقدار متوسط یا میانگین یک سیگنال متناوب متقارن، مانند یک سیگنال سینوسی، باید مقدار متوسط اندازه‌گیری شده در نصفی از یک دوره تناوب به عنوان ولتاژ متوسط در نظر گرفته شود. زیرا همان طور که گفتیم، مقدار میانگین یک سیگنال متناوب در یک دوره تناوب کامل، علی رغم مقدار پیک آن، برابر با صفر به دست خواهد آمد. به همین دلیل سیگنال را در نصفی از دوره تناوب خود در نظر می‌گیریم.
عبارت ولتاژ متوسط یا ولتاژ میانگین و نیز جریان متوسط را می‌توان هم در تجزیه و تحلیل مدارات AC و هم در مدارات DC مورد استفاده قرار داد. نمادی که برای نشان دادن ولتاژ متوسط به کار می‌رود، به صورت $$ V _ {A V } $$ است. همچنین برای نمایش جریان متوسط از نماد $$ I _ { AV } $$ استفاده می‌شود.
محاسبه ولتاژ متوسط با روش گرافیکی
همان طور که گفتیم، برای محاسبه مقدار ولتاژ متوسط باید سیگنال را در یک نیمه از دوره تناوب آن در نظر بگیریم. مقدار ولتاژ متوسط یا میانگین یک سیگنال را می‌توان از طریق مقادیر با فواصل برابر، با دقت قابل قبولی به دست آورد. نیمه مثبت شکل موج را به n قسمت برابر تقسیم می‌کنیم که به هر بخش یک فاصله میانی (Mid-Ordinate) می‌گوییم. عرض هر قسمت برابر با n درجه یا t ثانیه است. ارتفاع هر نیمه نیز برابر با مقدار لحظه‌ای شکل موج در آن نقطه در راستای محور x در نظر گرفته می‌شود. در تصویر زیر نمایی از روش محاسبه ولتاژ میانگین به روش گرافیکی نشان داده شده است.
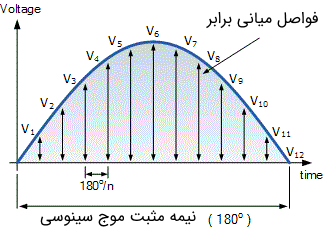
هر مقدار فاصله میانی از شکل موج ولتاژ به مقدار فاصله میانی قبلی افزوده می‌شود و مجموع کل مقادیر از $$ V _ 1 $$ تا $$ V _ { 12 } $$ بر تعداد فاصله میانی‌های استفاده شده تقسیم می‌شود. این مقدار به دست آمده برابر با ولتاژ متوسط سیگنال است. بنابراین می‌توان گفت که مقدار ولتاژ متوسط یا $$ V_ { AV } $$ برابر با میانگین ریاضی مجموع فاصله میانی‌های شکل موج ولتاژ است:
$$ V _ { A V } = \frac { \text { sum of all the mid-ordinates } } { \text { number of mid-ordinates } } $$
برای مثال ساده بالا، ولتاژ متوسط را می‌توان به صورت زیر محاسبه کرد:
$$ V _ { A V } = \frac { V _ 1 + V _ 2 + V _ 3 + V _ 4 + V _ 5 + ... + V_ { 11 } + V _ { 12 } } { 12 } $$
حال فرض کنید که یک ولتاژ متناوب با پیک ولتاژ ۲۰ ولت در یک نیم سیکل به صورت زیر تغییر می‌کند.
| ولتاژ (ولت) | $$ 6.2 $$ | $$ 11.8 $$ | $$ 16.2 $$ | $$ 19 $$ | $$ 20 $$ | $$ 19 $$ | $$ 16.2 $$ | $$ 11.8 $$ | $$ 6.2 $$ | $$ 0 $$ |
| زاویه | $$ 18 ^ o $$ | $$ 36 ^ o $$ | $$ 54 ^ o $$ | $$ 72 ^ o $$ | $$ 90 ^ o $$ | $$ 108 ^ o $$ | $$ 126 ^ o $$ | $$ 144 ^ o $$ | $$ 162 ^ o $$ | $$ 180 ^ o $$ |
با توجه به مقادیر فوق، مقدار ولتاژ متوسط به صورت زیر محاسبه می‌شود:
$$ V _ { A V } = \frac { 6.2 + 11.8 + 16.2 + 19 + 20 + 19 + 16.2 + 11.8 + 6.2 + 0} { 10 } $$
$$ V _ { A V } = \frac { 126.4 } { 10 } = 12. 64 \; \text {volts } $$
بنابراین مقدار ولتاژ متوسط برای یک نیم سیکل با استفاده از روش گرافیکی برابر با ۱۲٫۶۴ ولت به دست می‌آید:
محاسبه ولتاژ متوسط به روش عددی
همان طور که قبلا بیان کردیم، مقدار ولتاژ متوسط یک شکل موج متناوب که دو نیم سیکل آن دقیقا با یکدیگر مشابه اما دارای علامت مختلف باشند، برابر با صفر خواهد بود. البته توجه کنید که این مقدار برای تمام سیگنال‌های پریودیک سینوسی یا غیرسینوسی در یک دوره تناوب کامل صادق است. بنابراین برای محاسبه مقدار ولتاژ متوسط، باید مقادیر لحظه‌ای را در طول یک نیم سیکل از سیگنال با یکدیگر جمع کنیم.
اما اگر سیگنال ولتاژ، یک شکل موج غیر متقارن یا پیچیده باشد، ولتاژ یا جریان متوسط را باید در طول تمام دوره تناوب در نظر گرفت. مقدار ولتاژ متوسط را می‌توان به صورت ریاضی و با استفاده از تقریب ناحیه زیر منحنی در بازه‌های مختلف به طول بازه محاسبه کرد. در تصویر زیر نمایی از نحوه محاسبه ولتاژ متوسط با تقریب ناحیه زیر نمودار نشان داده شده است.
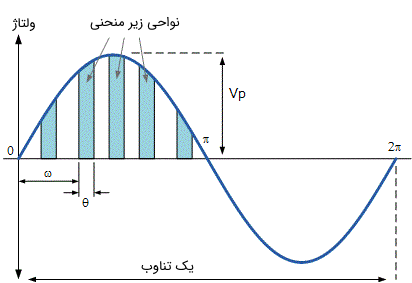
از طریق تقریب ناحیه مستطیلی یا مثلثی زیر نمودار، می‌توان یک ایده حدسی از ناحیه واقعی زیر هر بخش به دست آورد. حال با جمع کردن هر یک از این نواحی با یکدیگر، می‌توان مقدار ولتاژ متوسط را به دست آورد. اگر از تعداد بی‌نهایت ناحیه باریک‌تر مستطیلی شکل استفاده شود، آن‌گاه نتیجه نهایی از دقت بالاتری برخوردار خواهد بود؛ زیرا به $$ \frac { 2 } { \pi } $$ نزدیک‌تر می‌شود.
ناحیه زیر نمودار را می‌توان به روش‌های مختلفی به دست آورد. از جمله این روش‌ها می‌توان به قاعده ذوزنقه‌ای، قاعده فاصله میانی و قاعده سیمپسون (Simpson) اشاره کرد. بنابریان ناحیه زیر نیم سیکل مثبت از یک سیگنال متناوب با دوره تناوب T، که با رابطه $$ V ( t ) = V _ P cos ( \omega t) $$ تعریف می‌شود را می‌توان با استفاده از انتگرال و به صورت زیر به دست آورد:
$$ \text { Area } = \int_{0}^{ \pi} V _ P \; sin ( \omega t ) dt $$
در رابطه فوق، مقادیر ۰ و $$ \pi $$ برابر با کران‌های انتگرال هستند؛ زیرا ما قصد داریم مقدار ولتاژ متوسط را در طول یک نیم سیکل از شکل موج ولتاژ محاسبه کنیم. بنابراین با استفاده از فرمول بالا، نهایتا ناحیه زیر منحنی را برابر با $$ 2 V _ P $$ به دست می‌آوریم. حال که مقدار ناحیه زیر نیم سیکل مثبت (یا منفی) از منحنی را می‌دانیم، می‌توانیم به راحتی مقدار ولتاژ متوسط متعلق به نیم سیکل مثبت (یا منفی) را از طریق انتگرال‌گیری از مقدار سینوسی در طول یک نیم سیکل و تقسیم کردن بر نصف مقدار دوره تناوب به دست آوریم.
به عنوان مثال، اگر معادله ولتاژ سینوسی به صورت $$ V = V _ P \; sin ( \theta ) $$ داده شده باشد و دوره تناوب این سیگنال برابر با $$ 2 \pi $$ باشد، آن‌گاه برای محاسبه ولتاژ متوسط باید به صورت زیر عمل کنیم:
$$ V _ { AV } = \frac { 1 } { \pi } \int_{0}^{ \pi} V _ P \; sin ( \theta ) d \theta $$
$$ V _ { AV } = \frac { V _ P } { \pi } ( - cos \theta ) _0 ^ \pi $$
$$ = \frac { 2 V _ P } { \pi } = \frac { 2 } { \pi } V_ P = 0.637 V _ P $$
بنابراین معادله استاندارد برای محاسبه ولتاژ متوسط یک شکل موج سینوسی را می‌توان به صورت زیر نوشت:
$$ V _ { AV } = \frac { 2 V _ P } { \pi } = 0.637 V _ P $$
پس نتیجه می‌گیریم که ولتاژ متوسط یک شکل موج سینوسی، با ضرب کردن ولتاژ پیک سیگنال در عدد ثابت ۰٫۶۳۷ به دست می‌آید که این عدد حاصل تقسیم ۲ بر عدد $$ \pi $$ است. بنابراین مقدار ولتاژ متوسط که می‌توان به آن ولتاژ میانگین نیز گفت، به دامنه شکل موج بستگی دارد و به هیچ وجه تابعی از فرکانس یا زاویه فاز آن نیست.
بنابراین این مقدار متوسط که می‌تواند متعلق به یک شکل موج ولتاژ یا جریان سینوسی باشد را نیز می‌توان به صورت یک مقدار DC معادل از ناحیه و زمان نشان داد. در تصویر زیر نمایی از ناحیه ولتاژ متوسط در سیگنال با شکل موج سینوسی نشان داده شده است.
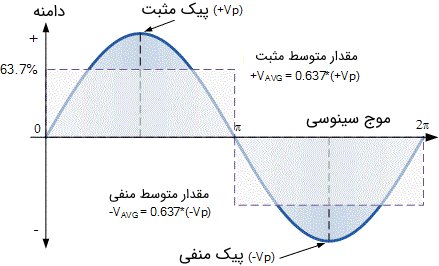
همان طور که در تصویر فوق می‌بینید، مقدار میانگین سیگنال در یک دوره تناوب کامل برابر با صفر است؛ زیرا در جمع نواحی، مقدار میانگین در نیم سیکل مثبت توسط مقدار میانگین در نیم سیکل منفی خنثی می‌شود ($$ V _ { AV } + (- V_ { AV } ) $$) و در نهایت مقدار ولتاژ متوسط در یک دوره تناوب کامل سیگنال سینوسی برابر با عدد صفر به دست می‌آید.
حال در مسئله‌ای که ولتاژ میانگین را به روش گرافیکی محاسبه کردیم، دیدیم که مقدار ولتاژ پیک ($$ V _ { PK } $$) برابر با ۲۰ ولت در نظر گرفته شده بود. برای همین مسئله، با استفاده از روش عددی مقدار ولتاژ متوسط را می‌توان به صورت زیر محاسبه کرد:
$$ V _ {AV } = V _ { PK } \times 0. 637 = 20 \times 0.637 = 12. 74 \; \text { volts } $$
با دقت در فرمول فوق، مشاهده می‌کنید که عدد به دست آمده به عنوان ولتاژ متوسط با استفاده از روش عددی دارای اختلاف بسیار کمی با مقدار ولتاژ متوسط به دست آمده با استفاده از روش گرافیکی است.
حال می‌خواهیم مقدار ولتاژ پیک را با در دست داشت مقدار ولتاژ متوسط محاسبه کنیم. برای این کار، باید فرمول را بازنویسی کنیم و سپس آن را بر یک عدد ثابت تقسیم نماییم. به عنوان مثال، می‌خواهیم مقدار ولتاژ پیک $$ V _ { PK } $$ یک سیگنال را در صورتی به دست بیاوریم که مقدار متوسط آن برابر با ۶۵ ولت باشد. برای این کار محاسبات را به صورت زیر انجام می‌دهیم:
$$ V _ { PK } = V _ { AV } \div 0. 637 = 65 \div 0.637 = 102 \; \text { volts } $$
توجه کنید که ضرب کردن مقدار پیک یا بیشینه در یک عدد ثابت 0٫۶۳۷ فقط به سیگنال‌هایی با شکل موج سینوسی قابل اعمال است.
مقایسه ولتاژ متوسط و ولتاژ موثر
در این مطلب به بررسی نحوه محاسبه مقدار ولتاژ متوسط یا جریان متوسط یک سیگنال پرداختیم. هنگامی که با یک ولتاژ یا جریان متناوب رو‌به‌رو می‌شویم، عبارت مقدار میانگین (Average Value) را معمولا برای یک دوره تناوب کامل مورد استفاده قرار می‌دهیم. در حالی‌که عبارت مقدار متوسط (Mean Value) بیشتر برای یک نیم سیکل از سیگنال متناوب استعمال می‌شود.
مقدار ولتاژ میانگین در طول یک دوره تناوب کامل از شکل موج سینوسی برابر با صفر به دست می‌آید. زیرا مقادیر موجود در دو نیم سیکل مثبت و منفی از سیگنال یکدیگر را خنثی می‌کنند. مقدار متوسط یک سیگنال سینوسی ولتاژ یا جریان را می‌توان با ضرب کردن ۰٫۶۳۷ در مقدار پیک سیگنال ولتاژ یا جریان محاسبه کرد. این رابطه ریاضی بین مقدار میانگین و مقدار پیک سیگنال را می‌توان هم به سیگنال‌های AC و هم به سیگنال‌های DC اعمال کرد.
گاهی اوقات لازم است که مقدار ولتاژ یا جریان مستقیم خروجی از یک مدار یکسوساز (Rectifier) یا یک مدار نوع پالس مانند مدار PWM موتور را محاسبه کرد. زیرا در این مدارات ولتاژ و جریان با اینکه معکوس نمی‌شوند، اما به صورت پیوسته تغییر می‌کنند. در این کاربردها، هیچ معکوس‌سازی فازی وجود ندارد، بنابراین مقدار RMS سیگنال اهمیتی ندارد و در عوض باید از مقدار متوسط سیگنال استفاده کرد.
تفاوت اصلی بین مقدار RMS یک سیگنال و مقدار متوسط آن، در این است که مقدار متوسط سیگنال متناوب برابر با میانگین تمام مقادیر لحظه‌ای یا تمام نواحی زیر نمودار در یک تناوب خاص از شکل موج است. اگر شکل موج مورد نظر ما یک سیگنال سینوسی باشد، این دوره تناوب را برابر با یک نیم سیکل از موج کامل در نظر می‌گیریم. برای راحتی معمولا نیم سیکل مثبت سیگنال را در نظر می‌گیرند.
از طرف دیگر، مقدار موثر یا مقدار RMS یک سیگنال را برابر با مقدار گرمای موثر حاصل از یک سیگنال در مقایسه با مقدار DC پایدار در نظر می‌گیرند. این مولفه از طریق ریشه یا جذر مجموع مربعات مقادیر لحظه‌ای یک سیگنال در طول یک دوره تناوب کامل از آن محاسبه می‌شود.
فقط برای یک شکل موج سینوسی خالص، می‌توان مقادیر ولتاژ یا جریان متوسط و نیز ولتاژ یا جریان RMS را با فرمول‌های ساده شده زیر محاسبه کرد:
$$ \text { Average value } = \text { maximum or peak value }(V _ { PK }) \times 0. 637 $$
$$ \text { RMS value } = \text { maximum or peak value }(V _ { PK }) \times 0. 707 $$
در تصویر زیر نمایی از مقایسه نحوه به دست آوردن مقدار متوسط و نیز مقدار RMS یک سیگنال سینوسی نشان داده شده است.
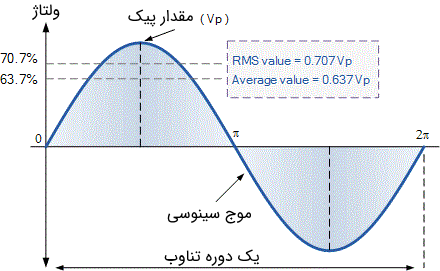
در مورد استفاده از مقدار متوسط و نیز مقدار RMS یک شکل موج، می‌توان به یک نکته دیگر نیز اشاره کرد. از هر دو مقدار می‌توان برای نشان دادن ضریب شکل (Form Factor) یک سیگنال سینوسی متناوب استفاده کرد. ضریب شکل به عنوان شکل یک سیگنال AC تعریف می‌شود و به صورت حاصل تقسیم مقدار RMS ولتاژ بر مقدار متوسط آن محاسبه می‌شود:
$$ \text {form factor = rms value/average value} $$
بنابراین برای یک شکل موج سینوسی یا پیچیده، مقدار ضریب شکل برابر با $$ \frac { \pi } { 2 \sqrt { 2 } } $$ محاسبه می‌شود که تقریبا برابر با عدد ثابت 1٫۱۱ است. توجه کنید که ضریب شکل هیچ واحد الکتریکی ندارد. اگر ضریب شکل یک سیگنال سینوسی را داشته باشیم، آن‌گاه با استفاده از مقدار ولتاژ RMS می‌توانیم مقدار ولتاژ متوسط را با توجه به فرمول فوق محاسبه کنیم و بر عکس این قضیه هم صادق است؛ زیرا مقدار ولتاژ متوسط برابر با ۰٫۹ ضرب در مقدار ولتاژ RMS یک سیگنال سینوسی است.
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد می‌شوند:
مرضیه خانم خیلی ممنون کلی از مطلبتون استفاده کردم
عالی بود
درود
و سپاس از دانش ی ک در اختیار عموم قرار دادید
مفید و کاربردی
لدفا کمی با زبان سادهتر هم بفرمایید تا خواننده توجیه بشد و بعد از خواندن , دنبال کسی نگرده که مطلبو براش توجیه کنه
سپاسم