نظریه مجموعه در ریاضیات | مفاهیم اولیه و کاربردها

نظریه مجموعه (Set Theory) شاخه‌ای از منطق ریاضی است که مجموعه‌ها را مورد مطالعه قرار می‌دهد. به طور غیررسمی تعریف مجموعه براساس اعضای آن صورت می‌گیرد. اگرچه هر نوع شیئ را می‌توان در یک مجموعه جمع آوری کرد، اما نظریه مجموعه بیشتر روی اشیایی که با ریاضیات در ارتباط هستند (یعنی مثلا اعداد یا ساختارهای ریاضیاتی) متمرکز است. با استفاده از زبان نظریه مجموعه می‌توان همه شاخه‌های ریاضی را بازسازی کرد. یکی از تلاش‌های ریاضیدانان این است که اصول و قضیه‌های معروف در ریاضیات را با نظریه مجموعه هماهنگ کنند.

از زبان نظریه مجموعه می‌توان برای تعریف تقریباً همه اشیاء ریاضی استفاده کرد. به همین منظور این نوشتار از مجموعه فرادرس را به نظریه مجموعه اختصاص داده‌ایم. برای آشنایی بیشتر با مفاهیم به کار رفته در این مطلب بهتر است نظریه اعداد و کاربردهای آن — به زبان ساده و میدان، حلقه و گروه در ریاضی — مفاهیم اولیه را مطالعه کنید. همچنین خواندن قواعد بخش پذیری یا عاد کردن — به زبان ساده و رابطه و تابع از نگاه مجموعه‌ ها — به زبان ساده نیز خالی از لطف نیست.

نظریه مجموعه

مطالعه مدرن نظریه مجموعه در دهه 1870 توسط «جورج کانتور» (Georg Cantor) (یا گئورگ کانتور) و «ریچارد ددکیند» (Richard Dedekind) آغاز شد. پس از کشف پارادوکس‌هایی در نسخه اولیه نظریه مجموعه، مانند «پارادوکس راسل» (Russell's Paradox)، سیستم‌های اصول‌گرای متعددی در اوایل قرن بیستم ابداع و مطرح شد. از این میان می‌توان به اصول «زرملو-فرانکل» (Zermelo–Fraenkel axioms)، با توجه به اصل انتخاب یا بدون آن، اشاره کرد که خوش‌نام‌تر و شناخته‌ شده‌‌تر است.

فیلم آموزش مبانی منطق و نظریه مجموعه ها در فرادرس

کلیک کنید

نظریه مجموعه به عنوان یک سیستم پایه برای ریاضیات بکار می‌رود، به ویژه در قالب نظریه مجموعه «زرملو-فرانکل» به همراه «اصل موضوعه انتخاب» (Axiom of Choice) ریاضیدانان بیشترین بهره را برده‌اند. ورای نقش اساسی این نظریه در ریاضیات، خود نظریه مجموعه به عنوان یک نظریه از شاخه‌های ریاضیات، هواداران و علاقمندان خود را در سال‌های اخیر پیدا کرده است. این شاخه از ریاضی دارای گستره وسیعی از حیطه‌های مختلف ریاضی از جمله «مجموعه اعداد حقیقی» (Real Numbers Line) تا «سازگاری اعداد اصلی بزرگ» (Consistency of Large Cardinals) را شامل می‌شود.

نکته: اصل موضوعه انتخاب بیان می‌کند که اگر تعداد مجموعه ناتهی (متناهی یا نامتناهی شمارا) در اختیار داشته باشیم، می‌توان مجموعه‌ای با انتخاب فقط یک عضو از هر یک از آن‌ها تشکیل داد. از آنجایی که این موضوع یک اصل محسوب می‌شود، اجباری در اثبات آن وجود ندارد. البته قبول این اصل به اثبات بسیاری از قضیه‌های مرتبط با نظریه مجموعه کمک خواهد کرد.

تاریخچه نظریه مجموعه

مباحث ریاضی به طور معمول از طریق تعامل بین بسیاری از محققان، ظهور و تکامل یافته است. نظریه مجموعه، با این حال، در سال 1874 توسط یک مقاله واحد در سال 1874 توسط «جورج کانتور» بنیانگذاری شد. این مقاله به نام «خصوصیات مجموعه اعداد حقیقی» (On a Property of the Collection of All Real Algebraic Numbers) منتشر شد. در این قضیه مقادیر بی‌نهایت که برای مجموعه اعداد نامتناهی در نظر گرفته شده بودند، دارای ترتیب شدند.

از زمان پیدایش ریاضیات و هندسه، ریاضیدانان با مفهوم بی نهایت مواجه شده و سعی در توجیه آن داشتند. در این بین مطالعات «برنارد بولزانو» (Bernard Bolzano) در نیمه اول قرن 19، قابل توجه است. درک مدرن از «بی‌نهایت» (Infinity) در دهه هفتم از قرن ۱۹ پدید آمد و توسط «کانتور» مورد تجزیه و تحلیل واقعی قرار گرفت. جلسه‌ای در سال 1872 بین «کانتور» و «ریچارد ددکیند» بر تفکر کانتور تأثیر گذاشت و منجر به انتشار مقاله معروف کانتور شد.

مطالعات و مقالاتی که کانتور در آن سال‌ها منتشر کرد، ریاضیدان‌ها را به دو گروه تقسیم کرد. گروهی مانند «کارل وایرشتراس» (Karl Weierstrass) و «ددکیند» از «کانتور» حمایت می‌کردند و در گروه دیگر «لئوپولد کرونکر» (Leopold Kronecker) و طرفدارانش قرار گرفته بودند که در مقابل ایده‌های کانتور مقاومت می‌کردند. البته «کرونکر»، امروزه به عنوان بنیانگذار سازه گرایی در ریاضیات شهرت دارد ولی مقاومت سختی در مقابل کانتور انجام داد بطوری که منجر به کنارکشیدن «کانتور» از فعالیت‌های علمی شد و سال‌ها در بیمارستان روانی تحت مداوا قرار داشت.

نظریه مجموعه کانتور که براساس اصول کانتوری استوار بود، به زودی گسترش یافت و مفاهیمی مانند «تناظر یک به یک» (One to One Correspondence) بین دو مجموعه مرسوم و کاربردی شد. این مفهوم نشان داد که تعداد اعداد حقیقی بسیار بیشتر از اعداد صحیح است. مفهوم «عدد اصلی» (Cardinal) و رابطه بین اعداد اصلی، شاخه‌ای مهم از ریاضیات جدید را بنیاد نهاد که باعث شد این نظریه به عنوان پایه‌ای برای شاخه‌های دیگری از ریاضیات دیده شود.

موج هیجان انگیز بعدی در نظریه مجموعه در حدود سال 1900 رخ داد، هنگامی که بعضی از ریاضیدانان متوجه شدند که از تفسیرهای صورت گرفته از نظریه مجموعه کانتور، منجر به ایجاد تناقضات متعددی شده است که یکی از آن‌ها به «پارادوکس راسل» شهرت دارد.

«مجموعه همه مجموعه‌ها که عضو خودشان نیستند» را در نظر بگیرید. این مجموعه باعث ایجاد یک تضاد یا تناقض می‌شود. اگر این مجموعه شامل همه مجموعه‌ها است، باید خودش را هم شامل بشود زیرا می‌دانیم که خود این شئی نیز یک مجموعه است. از طرفی این مجموعه شامل خودش نیست. در نتیجه تناقض شکل گرفته و نمی‌توان به درستی تعریفی از این مجموعه ارائه داد.

ولی وجود این گونه تناقض‌ها نتوانست جلوی پیشرفت نظریه مجموعه را بگیرید. مطالعات «ارنست زرملو» (Ernst Zermelo) در سال 1908 و تحقیقات «آبراهام فرانکل» (Abraham Fraenkel) و «تورالف اسکولم» (Thoralf Skolem) در سال 1922 منجر به مجموعه‌ای از اصول گردید که به اصول ZFC معروف است و نظریه مجموعه براساس آن‌ها شکل می‌گیرد.

نکته: عبارت ZFC دلالت بر « نظریه زرملو-رفانکل با اصل موضوع انتخاب» (Zermelo-Fraenkel with axiom of Choice) دارد.

ریاضیدانانی همچون «هنری لبگ» (Henri Lebesgue) بیشترین بهره را از نظریه مجموعه در نظریه خود با موضوع «اندازه لبگ» (Lebesgue Measure) و «انتگرال لبگ» (Lebesgue Integration) بردند. فعالیت‌های لبگ بخصوص در آنالیز ریاضی و احتمال، باعث ظهور شاخه‌ای مدرن در ریاضیات و «نظریه اندازه» (Measure Theory) گردید.

نمادها و مفاهیم اولیه

تئوری مجموعه با یک رابطه دو ضابطه‌ای بین یک شیء و مجموعه A شروع می‌شود. اگر o عضو (یا عنصری از) مجموعه A باشد، از علامت یا نماد $$o \in A$$ استفاده می‌شود. ساختار نمایشی برای یک مجموعه به صورت معرفی اعضای آن و جداسازی با علامت کاما (,) در داخل علامت‌های $$\{$$ و $$\}$$ صورت می‌گیرد. به این ترتیب اعضای یک مجموعه در رابطه عضویت صدق می‌کنند.

$$ \large \text{Membership Function} = \begin{cases} 1, & o \in A \\ 0, & o \notin A \end{cases} $$

فیلم آموزش ریاضی – پایه نهم در فرادرس

کلیک کنید

رابطه بالا نشانگر «تابع عضویت» (Membership Function) است. به این ترتیب می‌توانیم بین دو مجموعه $$A$$ و $$B$$ عملگر و رابطه‌های زیر را در نظر بگیریم.

• اگر همه اعضای مجموعه A نیز عضو مجموعه B باشند، A زیر مجموعه‌ای از B خواهد بود. این موضوع را با استفاده از نماد $$A \subseteq B $$ نشان می‌دهیم. به عنوان مثال $$\{1,2\}$$ زیر مجموعه $$\{1,2,3,\}$$ است. همچنین $$\{2\}$$ نیز زیر مجموعه $$\{1,2,3\}$$ محسوب می‌شود ولی $$\{4\}$$ زیرمجموعه آن نیست. در ضمن مشخص است که $$\{1,2,3\}$$ زیرمجموعه خودش است.

همانطور که از این تعریف تلقی می‌شود که هر مجموعه‌ای زیر مجموعه خودش است. در مواردی که بخواهیم این موضوع را از تعریف زیرمجموعه خارج کنیم از عبارت «زیرمجموعه صریح» (Proper Subset) یا مطلق استفاده می‌کنیم. در این صورت مجموعه $$A$$ زیرمجموعه صریح از مجموعه $$B$$ است اگر و فقط اگر $$A$$ زیر مجموعه $$B$$ بوده ولی با آن برابر نباشد. همانطور که عملگرهای دو پارامتری زیادی روی اعداد (نظیر جمع، ضرب، تقسیم و تفریق) اعمال می‌شود، مجموعه‌ها نیز دارای عملگرهای دو پارامتری هستند. در ادامه به معرفی بعضی از آن‌ها می‌پردازیم.

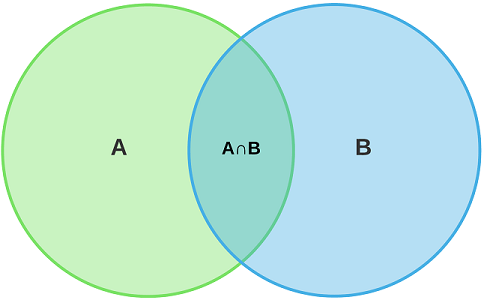
• اتحاد (Union) مجموعه‌های A و B با علامت $$A \cup B $$ مشخص شده و بیانگر مجموعه‌ای از همه اشیاء است که عضو A یا B یا هر دو هستند. اتحاد دو مجموعه $$\{1,2,3\}$$ با $$\{2,3,4\}$$ برابر است با $$\{1,2,3,4\}$$
• اشتراک (Intersection) مجموعه‌های A و B با علامت $$ A \cap B$$ نمایش داده شده و مجموعه‌ای از همه اشیایی است که هم عضو A هستند و هم عضو B. اشتراک دو مجموعه $$\{1,2,3\}$$ و $$\{2,3,4\}$$ برابر است با $$\{2,3\}$$.
• تفاضل (Subtraction) یا اختلاف مجموعه‌ای (Set Difference) مجموعه  U از  A با علامت $$U\ \text \ A$$، مجموعه‌ای از اعضای U است که عضو A نیستند. اختلاف $$\{1,2,3\} \text\ \{2,3,4\}$$ برابر است با $$\{1\}$$. در عوض، اختلاف $$\{2 , 3 , 4\} \text \ \{1 , 2 , 3\} $$ برابر است با $$\{4\}$$.

هنگامی که A زیرمجموعه U است، تفاوت مجموعه U \ A را به عنوان متمم (Complement) مجموعه A نسبت به U نیز می‌نامیم. در این حالت، اگر مجموعه U مجموعه مشخصی باشد که همه نسبت به آن آگاهی دارند، مجموعه متمم $$A$$ را نسبت به $$U$$ با نماد $$A^c$$ یا $$A^\prime$$ مشخص می‌کنند. در این حالت مجموعه $$U$$ را «مجموعه جهانی» (Universal Set) می‌نامند. منظور از مجموعه جهانی، مجموعه‌ای است که همه اعضای موضوع مورد بحث را شامل می‌شود.

• تفاضل متقارن (Symmetric difference) مجموعه‌های A و B با علامت $$ A\ \Delta \ B$$ یا $$ A \ominus B $$ نشان می‌دهند. تفاضل متقارن $$A$$ از $$B$$، مجموعه‌ای از همه اشیاء است که دقیقاً عضو مجموعه‌های A یا B هستند، اما در هر دو آن‌ها قرار ندارند. به عنوان مثال، برای مجموعه‌های $$\{1,2,3\}$$ و $$\{2,3,4\}$$ تفاضل متقارن برابر است با $$\{1,4\}$$. به بیان دیگر تفاضل متقارن، اختلاف مجموعه‌ای بین اجتماع و اشتراک دو مجموعه است. یعنی $$ A\ \Delta \ B = (A \cup B‌) \text\ (A \cap B) $$ است و از طرفی نیز رابطه $$ A\ \Delta \ B = (A\ \text\ B) \cup (B \ \text\ A)$$ برقرار خواهد بود.

• ضرب دکارتی (Cartesian Product) مجموعه A در B، با علامت $$ A \times B $$، مجموعه‌ای است که اعضای آن همه جفت‌های مرتب به شکل $$(a,b)$$ هستند که در آن a عضو A است و b عضو B است.  ضرب دکارتی $$\{1, 2 ,2 \} $$ در $$\{ \text{Red}, \text{White}\}$$ برابر است با:

$$ \large \{1 , 2 \} \times \{\text{Red}, \text{White}\} = \{(1, \text{White}), (2,\text{White}), (1,\text{ Red}) , (2,\text{Red})\}$$

• مجموعه توانی (Power Set) برای مجموعه A، مجموعه‌ای است که اعضای آن همگی از  زیر مجموعه‌های A تشکیل شده‌اند. به عنوان مثال، مجموعه توانی برای $$\{1,2\}$$ برابر است با $$\{\{1\},\{2\},\{1,2\},\emptyset\}$$. از اعضای مهم در مجموعه توانی، می‌توان به خود مجموعه $$A$$ و مجموعه تهی ($$\emptyset$$) اشاره کرد.

مجموعه‌های مهم و موثر در نظریه مجموعه، مجموعه تهی (که شامل هیچ عضوی نیست)، مجموعه اعداد طبیعی، مجموعه اعداد حقیقی و همچنین مجموعه اعداد مختلط هستند که بخصوص در نظریه اعداد و آنالیز مختلط به کار می‌روند.

هستی شناسی در نظریه مجموعه

یک مجموعه را «خالص» (Pure Set) می‌گوییم، اگر تمام اعضای آن، مجموعه باشند، همچنین تمام اعضای آن مجموعه‌ها نیز مجموعه باشند و غیره. به عنوان مثال، مجموعه {{}} که فقط شامل مجموعه تهی است، یک مجموعه خالص غیر تهی است.

فیلم آموزش مبانی منطق و نظریه مجموعه ها در فرادرس

کلیک کنید

در تئوری مجموعه مدرن، معمولا توجه را به مجموعه جهانی «ون نویمان» از مجموعه‌های خالص معطوف می‌کنند. بسیاری از سیستم‌های «نظریه مجموعه اصول‌گرا» (Axiomatic Set Theory)، به منظور اصل‌سازی روی مجموعه‌های خالص که توسط جان نویمان معرفی شدند، طراحی و ایجاد شده‌اند.

برای این موضوع مزایای فنی زیادی وجود دارد و کلیت نظریه مجموعه از بین نمی‌رود، زیرا اساساً همه مفاهیم ریاضی می‌توانند توسط مجموعه‌های خالص مدل‌بندی شوند. مجموعه‌های موجود در جهان «ون نویمان» در یک رابطه «سلسله مراتبی تجمیعی» ( Cumulative Hierarchy Relation) قرار می‌گیرند، بر اساس این که یک عضو چقدر در عمق این رابطه سلسله مراتبی قرار گرفته باشد، به هر مجموعه در این سلسله مراتب (با استفاده از رابطه بازگشتی) یک عدد ترتیبی مثل $${\displaystyle \alpha}$$ اختصاص داده که به عنوان رتبه آن شناخته می‌شود. رتبه یک مجموعه خالص $${\displaystyle X}$$ «کوچکترین کران بالایی» (Supremum) برای همه رتبه‌های اعضای $$ {\displaystyle X}$$ تعریف شده است.

به عنوان مثال، به «مجموعه تهی» رتبه 0 اختصاص داده می‌شود، در مقابل، مجموعه {{}} که حاوی فقط مجموعه خالی یا تهی است، رتبه 1 را دارد. برای هر مقدار $$\alpha$$ به عنوان ترتیب، مجموعه $$V_{\alpha}$$ بوسیله همه مجموعه‌های خالصی که دارای رتبه کمتر از $$\alpha$$ هستند، تعریف می‌شود.

نکته: اغلب در نظریه مجموعه و شاخه‌های مختلف آن، مجموعه جهانی فن نویمان را با $$V$$ نشان می‌دهند.

نظریه مجموعه اصل‌گرا

نظریه مجموعه مقدماتی را می توان به طور غیررسمی و بصری (نمودار ون- Venn Diagram) مورد مطالعه قرار داد، بنابراین می‌توان در مدارس ابتدایی با استفاده از نمودارهای ون به آموزش آن پرداخت. رویکرد شهودی نظریه مجموعه، بطور ضمنی فرض می‌کند که یک مجموعه ممکن است از کلاس همه اشیاء که در یک یا چند شرط خاص مشترک هستند، تشکیل شود. البته باید توجه داشت که این فرض پارادوکس ایجاد می‌کند که ساده‌ترین و مشهورترین آن‌ها، همانطور که قبلا نیز اشاره شد، «پارادوکس راسل» و «پارادوکس بورالی-فورتی» (Burali-Forti paradox) است. نظریه «مجموعه اصول‌گرا» (Axiomatic Set Theory) برای خلاصی نظریه مجموعه با چنین پارادوکس‌هایی ابداع شده است.

فیلم آموزش ریاضیات گسسته در فرادرس

کلیک کنید

گسترده‌ترین سیستم‌های مورد مطالعه نظریه مجموعه به شکلی بدیهی نشان می‌دهد که همه مجموعه‌ها یک سلسله مراتب تجمیعی را تشکیل می‌دهند. از دیدگاه «هستی‌شناسی» (Onthology) می‌توان آن‌ها را به گونه‌های زیر دسته‌بندی کرد.

• منحصراً مجموعه: این رویکرد شامل رایج‌ترین نظریه مجموعه یعنی نظریه مجموعه «زرملو-فرانکل» با «اصل موضوعه انتخاب» (Axiom of Choice) است که به اختصار (ZFC) خوانده می‌شود. اجزای اصلی ZFC به صورت زیر است.
  • «نظریه مجموعه زرملو»، که «اصل جایگذاری» (Axiom Schema of Replacement) را با «اصل تفکیک» (Separation) جایگزین می‌کند.
  • «نظریه مجموعه عمومی» (General Set Theory)، در بخش کوچکی با نظریه مجموعه زرملو تفاوت دارد، برای مجموعه‌های متناهی و به کارگیری «اصول پیانو» (Peano Axioms) مناسب است.
  • نظریه مجموعه «کریپکه-پلاتک» (Kripke-Platek)، که از بی‌نهایت، مجموعه توانی و همچنین اصل انتخاب صرف نظر کرده و دارای شرط‌های ضعیف‌تری برای اصول تفکیک و جایگذاری نسبت به نظریه زرملو است.
• مجموعه و کلاس‌های معین (Proper Class): این رویکرد، متناسب با «نظریه مجموعه فون نویمان-برنایز-گودل» (ٰVon Neumann–Bernays–Gödel set theory) است، که دارای همان قدرت ZFC برای قضایای مربوط به نظریه مجموعه‌ است. از طرفی نظریه مجموعه «مورس-کلیلی» (Morse–Kelley Set Theory) و نظریه مجموعه «تارسکی-گروتندیک» (Tarski–Grothendieck Set Theory)، هر دو قوی‌تر از ZFC هستند.

کاربردهای نظریه مجموعه

بسیاری از مفاهیم ریاضی را می‌توان دقیقاً با استفاده از نظریه مجموعه‌ها و اصول آن، تعریف و مورد بررسی قرار داد. به عنوان مثال، ساختارهای ریاضی مانند «گراف» (Graphs)، «منیفولدها» (Manifolds)، «حلقه‌ها» (Rings) و «فضاهای برداری» (Vector Space) توسط نظریه مجموعه قابل توصیف و اصل‌سازی هستند. همچنین «رابطه هم‌ارزی» (Equivalence) و «رابطه ترتیبی» (Order Relation) در ریاضیات بسیار فراگیر هستند و بسیاری از رابطه‌ها و ترتیب‌ها در ریاضیات را می‌توان در نظریه مجموعه توصیف کرد.

فیلم آموزش ریاضیات گسسته – حل تست کنکور کارشناسی ارشد در فرادرس

کلیک کنید

نظریه مجموعه همچنین یک سیستم بنیادی و پشتیبان برای بسیاری از شاخه‌های مختلف ریاضیات محسوب می‌شود. از زمان انتشار نخستین جلد کتاب Principia Mathematica، توسط «وایت‌هد» (Alfred North Whitehead) و «راسل» (Bertrand Russell) ادعا شده است که بیشتر یا حتی همه قضایای ریاضی را می‌توان با استفاده از مجموعه‌های طراحی شده در نظریه مجموعه، ایجاد و اثبات کرد. البته این کار بوسیله منطق مرتبه اول یا دوم میسر خواهد شد.

به عنوان مثال، خصوصیات «اعداد طبیعی» (Natural Numbers) و «اعداد حقیقی» (Real Numbers) را می‌توان در نظریه مجموعه بدست آورد، زیرا هر سیستم عدد با مجموعه‌ای از «کلاس‌های هم ارزی» (Equivalence Classes) تحت یک «رابطه هم ارزی» (Equivalence Relation) مناسب که میدان آن مجموعه نامتناهی است، قابل بیان است.

نقش نظریه مجموعه به عنوان پایه‌ای برای «آنالیز ریاضی» (Mathematical Analysis)، «توپولوژی» (Topology)، «جبر مجرد» (Abstract Algebra) و «ریاضیات گسسته» (Discrete Mathematics)، غیرقابل بحث است. همه ریاضیدانان پذیرفته‌اند که قضایای موجود در این گونه زمینه‌های مطالعاتی ریاضیات، می‌توانند از تعاریف و اصول نظریه مجموعه مشتق شوند.

البته تعداد کمی از قضیه‌های مربوط به نظریه‌های پیچیده ریاضی از طریق نظریه مجموعه به طور رسمی اثبات یا تأیید شده‌اند، زیرا چنین حوزه‌هایی اغلب به ادبیات پیشرفته‌تری در بین ریاضیدانان احتیاج دارند. در یکی از پروژه‌های تأیید شده به نام (Metamath)، بیش از 12000 قضیه ریاضی را براساس نظریه مجموعه ZFC، «منطق مرتبه اول» (First-order Logic) و «منطق گزاره‌ها» (Propositional Logic) اثبات شده است.

حیطه مطالعاتی

نظریه مجموعه یک حوزه اصلی تحقیق در ریاضیات است که دارای بسیاری از زمینه های مرتبط با هم است. در ادامه به بعضی از این حوزه‌ها، اشاره خواهیم کرد.

نظریه مجموعه ترکیبیاتی

«نظریه مجموعه ترکیبیاتی» (Combinatorial set theory)، مربوط به توسعه ترکیبات متناهی به حالت نامتناهی است که شامل مطالعه حسابی اعداد اصلی یا کاردینال و بررسی شاخه‌های مختلف «قضیه رمزی» (Ramsey's Theorem) مانند قضیه «اردوس-رادون» (Erdős-Rado) است.

فیلم آموزش ترکیبیات و کاربردها در فرادرس

کلیک کنید

نظریه مجموعه توصیفی

«نظریه مجموعه توصیفی» (Descriptive set theory)، به مطالعه زیرمجموعه‌های اعداد حقیقی و به طور کلی زیرمجموعه‌های «فضاهای لهستانی» (Polish Space) می‌پردازد. این کار با مطالعه «کلاس‌هایی از نقاط» (Pointclasses) در «سلسله مراتب بورل» (Borel Hierarchy) آغاز می‌شود و به مطالعه سلسله مراتب پیچیده‌تر مانند «سلسله مراتب تصویری» (Projective Hierarchy) ادامه می‌یابد.

بسیاری از خصوصیات «مجموعه‌های بورل» (Borel Sets) در ZFC قابل اثبات است، اما اثبات این ویژگی‌ها برای مجموعه‌های پیچیده‌تر نیاز به اصول اضافی مربوط به «اعداد اصلی بزرگ» (Large Cardinals) دارد.

کاردینال بزرگ

یک «کاردینال بزرگ» (Large Cardinals) یک عدد اصلی با یک خاصیت اضافی است. بسیاری از ویژگی‌های اعداد کاردینال بزرگ مانند «اندازه‌پذیری» (Measurable) مورد مطالعه قرار گرفته‌اند. این خصوصیات به طور معمول نشان می‌دهد که عدد اصلی یا کاردینال باید بسیار بزرگ باشند. با این حال اثبات وجودی برای اعداد کاردینال توسط نظریه مجموعه «زرملو-فرانکل» میسر نیست.

نظریه مجموعه فازی

فیلم آموزش نظریه مجموعه های فازی و کاربردهای آن در فرادرس

کلیک کنید

این دیدگاه به مجموعه و عضویت توسط ریاضیدان و مهندس برق، «لطفی زاده» (Lotfi A. Zadeh) معرفی و به نام «منطق فازی» (Fuzzy Logic) به کار رفت. این شیوه تفکر و راه و روش منطقی با چیزی که اغلب مردم در زندگی روزمره به کار می‌برند، بسیار مطابقت دارد. هر چند «زاده» از این نظریه، برای کنترل دستگاه‌های الکتریکی استفاده کرد.

برای مثال تعلق فردی به گروه بلند قدها، بسیار منعطف‌تر از دو وضعیت «بله» (Yes) و «خیر» (NO) است که در منطق باینری به کار می‌رود. برای مثال ممکن است تعلق فردی به این مجموعه در مجموعه فازی، برابر با 75٪ یا 0٫75 در نظر گرفته شود.

نظریه مجموعه در تحصیلات ریاضیاتی

از آنجا که تئوری مجموعه محبوبیت خود را به عنوان پایه و اساس ریاضیات مدرن به دست آورده است، در اوایل دوره آموزش ریاضیات، از ایده معرفی نظریه مجموعه براساس اصول اولیه می‌توان بهره گرفت.

در ایالات متحده آمریکا در دهه 1960، تجربه آموزش ریاضیات جدید با هدف آموزش پایه‌های نظریه مجموعه، از جمله مفاهیم انتزاعی، به دانش آموزان مقطع ابتدایی انجام شد. اما این کار بعدها با انتقادهای زیادی روبرو شد. برنامه درسی ریاضی در مدارس اروپایی از این روند پیروی کرده و در حال حاضر موضوع نظریه مجموعه را در مقاطع مختلف در همه رشته‌ها دخیل می‌کنند. نظریه مجموعه، برای آشنایی دانش آموزان به «اپراتورهای منطقی» (Logical Operators) مانند (NOT ، AND ، OR) استفاده می‌شود.

این کار ممکن است هنگام یادگیری برنامه‌نویسی رایانه نیز مفید باشد، زیرا مجموعه‌ها و «منطق بولی» (Boolean Logic)، بلوک‌های اساسی ساخت بسیاری از زبان‌های برنامه‌نویسی هستند. مجموعه‌ها معمولاً هنگام تدریس در مورد انواع مختلف اعداد مثل اعداد حقیقی (R)، اعداد صحیح (Z)، اعداد طبیعی (N) و غیره، هنگام تعریف توابع ریاضی به عنوان رابطه بین دو مجموعه، مورد استفاده قرار می‌گیرند.

خلاصه و جمع‌بندی

هر چند نظریه مجموعه پس از نظریه‌های زیادی در ریاضیات ظهور و مطرح گشته است، ولی به سرعت توانست جایگاه خود را در بین دیگر نظریه‌های ریاضی پیدا کرده و تبدیل به بخش از ریاضیات شود که همه شاخه‌های دیگر ریاضی از آن بهره می‌برند. اصول مطرح شده در نظریه مجموعه در حالت‌هایی، بسیار بدیهی و در بعضی از موارد بسیار پیچیده به نظر می‌رسند. ولی به هر حال امروزه قضیه و اصول این نظریه در اثبات بسیاری از قضیه‌های اساسی شاخه‌های دیگر ریاضی به کار برده شده و یاریگر دانشمندان ریاضی شده است.