مقیاس فاصله ای | ویژگی و کاربردهای آن – به زبان ساده
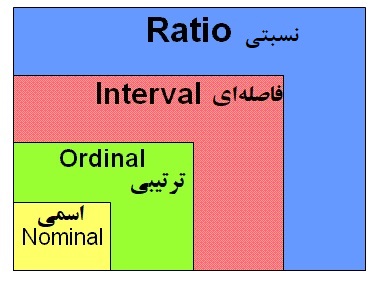
در سال 1946 میلادی، «استنلی اسمیت استیونز» (Stanley Smith Stevens) به منظور ثبت اطلاعات و دادههای آماری، چهار مقیاس اندازه گیری را معرفی کرد: «اسمی» (Nominal)، «ترتیبی» (Ordinal)، «مقیاس فاصله ای» (Interval) و «مقیاس نسبت» (Ratio). این مقیاسها، امروزه به طور گسترده به عنوان روشی برای توصیف ویژگیهای یک متغیر مورد استفاده قرار میگیرند. شناخت و آگاهی درباره مقیاسهای اندازهگیری برای یک متغیر، جنبه مهمی در انتخاب تحلیل آماری مناسب است. نوع مقیاس برای متغیرها و دادهها، روشنگر روشی است که در تحلیلهای آماری میتوان به کار برد.


برای آشنایی بیشتر با موضوع مقیاسبندی و انواع متغیرها در آمار بهتر است نوشتارهای جامعه آماری — انواع داده و مقیاسهای آنها و سطوح سنجش یا اندازه گیری | به زبان ساده را مطالعه کنید. همچنین خواندن انواع متغیرها در آمار | با مثال و به زبان ساده و استنباط آماری | مفاهیم اولیه و روشها — به زبان ساده نیز خالی از لطف نیست.
مقیاس فاصله ای
استفاده از دادهها و اطلاعات در تحلیلهای علمی و بخصوص آماری، از اهمیت زیادی برخوردار است. اغلب این گونه مقادیر و اطلاعات را به دو دسته «کمی» و «کیفی» طبقهبندی میکنیم تا نسبت به این طبقهبندی، کارایی و ویژگیهای آنها را مشخص کنیم. البته تبدیل دادههای کمی و کیفی به صورت عددی، با مقیاس و سطوح سنجش یا اندازهگیری میسر است. در این متن میخواهیم با یکی از این مقیاسها یعنی «مقیاس فاصلهای» (Interval Scale) آشنا شویم.
قبل از آن به سراغ مقیاس فاصله ای رفته و توضیحاتی در مورد آن در اختیارتان قرار دهیم، بهتر است ابتدای امر، در مورد مقیاس بندی و کاربردهای آن اطلاعاتی بیشتری داشته باشیم. در ادامه متن، به این موضوع پرداختهایم و مقیاسهایی که به مقیاسهای استیونز معروف هستند را مورد بررسی قرار داده ولی در مورد مقیاس فاصله ای بیشتر بحث کرده و با مثالهایی مفهوم آن را روشن خواهیم ساخت.

کاربرد مقیاس بندی
همانطور که اشاره شد، اعداد امکان بیان خصوصیات بسیاری از پدیدهها را دارند. بنابراین برای ویژگیهای کمی و حتی کیفی امکان توصیف پدیدهها به کمک اعداد وجود دارد. مقیاسبندی در حقیقت این تبدیل را برای محقق انجام میدهد. بهتر است ابتدا یک تعریف از مقیاس و سطوح سنجش ارائه دهیم.
تعریف: مقیاس گذاری و سطوح سنجش به معنی نسبت دادن یک عدد به یک کمیت یا کیفیت است که بوسیله یک قانون خاص صورت میگیرد. این قانون نباید به شکل تصادفی به کار رود و باید در همه حالتها، یکسان عمل کند.
تعریفی که ارائه شد، توسط «لوس» (R. Duncan Luce) آمار شناس امریکایی در سال ۱۹۸۶ معرفی گردید. او به تحلیل مقیاسهای استیونز پرداخت و بعضی از تعریفها را جابجا کرد. این دانشمند به این موضوع تکیه داشت که باید علاوه بر تعریف صحیح از مقیاسها، کاربرد و خصوصیات آنها نیز در عمل مشخص شود.

مقایسه فاصله ای و ویژگیهای آن
مقیاس فاصلهای یک مقیاس اندازهگیری مقادیر کمی است که در آن ترتیب و امکان مرتب سازی وجود دارد، از طرفی محاسبه اختلاف بین دو متغیر با این مقیاس امکانپذیر بوده و مقدار صفر در این مقیاس به صورت اختیاری یا قراردادی تعیین میشود. مقیاس فاصلهای سومین سطح سنجش یا اندازهگیری است که پس از مقیاس اسمی و مقیاس ترتیبی قرار میگیرد. درک دو سطح قبلی (اسمی و ترتیبی) به شما کمک میکند تا مقیاس فاصلهای را بهتر درک کرده و تفاوتها را بشناسید.
مقیاس اسمی زمانی استفاده میشود که متغیرها دارای یک ترتیب طبیعی یا رتبهبندی نباشند. به کمک این مقیاس میتوانید متغیرها را به صورت کدگذری، مقداردهی کنید. نمونههای رایج متغیرها با این مقیاس سنجش، شامل جنسیت، محل تولد، حزب سیاسی، نوع حیوانات خانگی و غیره است. در مقابل، در مقیاس ترتیبی، رتبهبندی روی مقادیر متغیرها امکانپذیر است. در این بین تفاوت یا فاصله بین مقادیر مرتب شده، اهمیت چندانی ندارد. برای مثال مقطع یا مدرک تحصیلی (زیر دیپلم، دیپلم، لیسانس، فوق لیسانس و دکتری) با مقیاس ترتیبی اندازهگیری میشود. توجه داشته باشید که در این مقیاس، فاصله بین مقدارهای مرتب شده معنی نداشته و فقط ترتیب قرارگیری آنها برتری را نشان میدهد.
ولی در الگو یا مقیاس بعدی فاصله بین مقادیر دارای معنی بوده و به واسطه آن، تحلیل و محاسبات بیشتری صورت میگیرد. به کمک مقیاس فاصلهای اختلاف بین مقادیر متغیرها معنی دار است و نسبت بین اختلاف مقادیر با تغییر واحد اندازهگیری یکسان خواهد بود. به این ترتیب اگر قرار است فاصله یا تفاضل بین مقادیر محاسبه و مقایسه شود، بهترین مقیاس سنجش، مقیاس فاصلهای خواهد بود. برای مثال، دما، فشار و زمان (ساعت) از مقادیری هستند که با مقیاس فاصله ای به کار گرفته میشوند.
نکته: به یاد داشته باشید که در مقیاس فاصلهای حتما یکا یا فاصله بین مقادیر در همه جا یکسان است.
هنگام استفاده از مقیاس فاصلهای میتوان اختلاف بین هر دو مقدار را با استفاده از تفریق محاسبه کرد. البته باید اشاره کرد که در این مقیاس، نسبت مقادیر معنایی ندارد ولی نسبت اختلاف دو مقدار متوالی همیشه ثابت است. در ادامه به کمک مثالهایی، کاربردهای مختلف مقیاس فاصلهای را معرفی و زوایای به کارگیری آن را بیشتر شرح خواهیم داد.
مقیاس فاصله ای و ذکر چند مثال از آن
در قسمت قبل اشاره کردیم که دما و زمان از مقادیری هستند که با مقیاس فاصلهای به کار گرفته میشوند. در این بخش میخواهیم به ذکر دو مثال بپردازیم و کاربردهای مقیاس فاصلهای را در چنین حالتهایی مشخص کنیم. البته توجه داشته باشید که pH یا میزان خاصیت اسیدی یا بازی مواد نیز با مقیاس فاصلهای اندازهگیری میشود و خصوصیات این مقیاس را دارد.
زمان و ساعت با مقیاس فاصله ای
در ابتدا سنجش زمان را به صورت ۱۲ ساعتی در نظر بگیرید. اختلاف بین ساعت ۴:۰۰ تا ۸:۰۰ بعد از ظهر معنیدار بوده و نشانگر یک طول زمانی ۴ ساعته است. اگر این بار زمانها را به صورت ۲۴ ساعتی در نظر بگیریم، فاصله بین همان ساعتها (۱۶:۰۰ و ۲۰:۰۰) باز هم برابر با ۴ ساعت خواهد بود. در نتیجه تغییر واحد اندازهگیری زمان، در نسبت فاصله تغییری ایجاد نخواهد کرد. این تفاضل را در نمودار زیر روی محورهای افقی نمایش دادهایم.
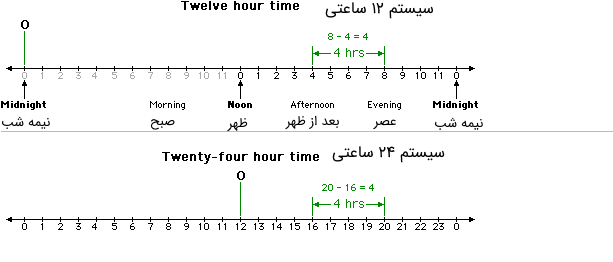
نکته: توجه داشته باشید که نسبت این دو ساعت در واحدهای مختلف برابر نیست و فقط نسبت فاصلهها یکسان خواهد بود. به نمودارهای زیر که نشانگر این وضعیت هستند، توجه کنید.

دما و مقیاس فاصله ای
معمولا از واحدهای «سلسیوس» (Celsius) یا سانتیگراد و «فارنهایت» (Fahrenheit) برای اندازهگیری دما استفاده میشود. در واحد سانتیگراد، مبدا یا مقدار صفر برای حرارت، دمای یخ زدن آب در نظر گرفته شده. از طرفی ۱۰۰ درجه هم دمای جوش آب محسوب شده است. فاصله بین این دو نقطه، به ۱۰۰ فاصله تقسیم شده است.

در مقابل فارنهایت، این فاصله را به 180 واحد تقسیم کرده و دمای یخ زدن آب را ۳۲ و دمای جوش را هم ۲۱۲ در نظر گرفت.
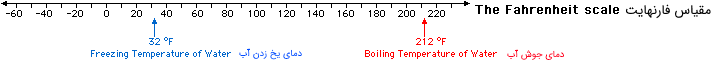
این بار دو دمای یخ زدن آب و جوش آمدن آن را با توجه به دو واحد اندازهگیری در نظر میگیریم. نسبت مقیاس سانتیگراد به فارنهایت برابر است با . همچنین این نسبت برای فارنهایت به سانتیگراد نیز به شکل خواهد بود. به این ترتیب برای تبدیل دما برحسب فارنهایت به سانتیگراد از رابطه زیر کمک میگیریم.
و برعکس به منظور نمایش دما و تبدیل از سانتیگراد به فارنهایت از فرمول زیر استفاده خواهیم کرد.
در ادامه نشان میدهیم که نسبت اختلاف دو دمای مختلف در واحد اندازهگیری سلسیوس با نسبت اختلاف همان دماها در واحد اندازهگیری فارنهایت، برابر است. دماهای زیر را در نظر بگیرید.
- 10 درجه سانتیگراد که معادل با ۵۰ درجه فارنهایت است.
- ۳۰ درجه سانتیگراد که معادل با 86 درجه فارنهایت است.
- ۴۰ درجه سانتیگراد که معادل با ۱۰۴ درجه فارنهایت است.
- ۶۰ درجه سانتیگراد که معادل با ۱۴۰ درجه فارنهایت است.
حال اختلافها را محاسبه میکنیم.
پس فاصله بین این دماها یکسان است. حال مقیاس را تغییر میدهیم و همین عملیات را براساس واحد فارنهایت اجرا میکنیم.
پس نسبت اختلاف دماها چه در واحد فارنهایت و چه در واحد سانتیگراد یکسان است. ولی این موضوع در مورد خود دماها صادق نیست. یعنی نسبت دمای اول و دوم (۱۰ درجه و ۳۰ درجه) در مقیاس سانتیگراد با نسبت همین دماها (50 و 86 درجه) در مقیاس فارنهایت یکی نیست.
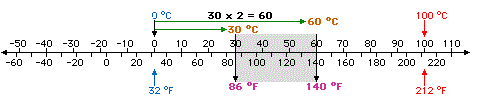
همانطور که دیده میشود، دمای ۳۰ درجه دو برابر دمای ۶۰ درجه در واحد اندازهگیری سلسیوس است در حالیکه دماهای معادل که 86 و 140 هستند این نسبت را ندارند و نمیتوان 140 را دو برابر دمای 86 درجه در نظر گرفت.
از طرفی میتوان تفاوت فاصله دمای صفر تا 60 درجه دو برابر فاصله بین دمای ۰ تا ۳۰ درجه در مقیاس سانتیگراد محسوب کرد. همین امر نیز در مقیاس فارنهایت برقرار است و میتوان دید که اختلاف بین دو دمای ۱۴۰ و ۳۲ درجه فارنهایت دو برابر اختلاف دمای ۸۶ تا ۳۲ درجه است. واضح است که این دماها معادل دماهای قبلی با مقیاس سانتیگراد هستند. پس نسبت فاصله بین دماها در هر دو واحد اندازهگیری حفظ شده است.
تفاوت و تشابه بین مقیاس فاصله ای با مقیاسهای دیگر
در جدول زیر به بعضی از ویژگیهای مقیاس فاصلهای و تشابه آن با مقیاسهای دیگر نمایش داده شده.
شاخصهای آماری قابل محاسبه برای هر یک از مقیاسهای استیونز نیز مورد اشاره قرار گرفته است.
جدول ۱: مقیاسهای سنجش و ویژگیهای آنها از لحاظ شاخصهای آماری
| نوع محاسبه | اسمی | ترتیبی | فاصلهای |
| جدول توزیع فراوانی (هیستوگرام) | OK | OK | OK |
| میانه و چندکها | NO | OK | OK |
| جمع و تفریق | NO | NO | OK |
| میانگین و انحراف استاندارد | NO | NO | OK |
| نسبت و محاسبه ضریب تغییرات | NO | NO | NO |
توجه داشته باشید که تفاوت اصلی بین متغیرهایی با مقیاس فاصلهای و نسبت (Ratio) آن است که صفر در مقیاس فاصلهای، مقداری قراردادی است. در نتیجه ضرب و تقسیم (نسبتگیری) در این مقیاس قابل استفاده نخواهد بود. در حالیکه در مقیاس نسبت، از همه نوع عملیات ریاضی میتوان بهره برد. همانطور که در جدول بالا مشاهده میکنید، به عنوان شاخصهای تمرکز برای متغیر اسمی فقط میتوان از مد استفاده کرد که از طریق جدول فراوانی قابل جستجو است.
کاربرد مقیاس فاصله ای
سوالات مطرح شده در یک پرسشنامه یکی از متداولترین روشهای جمعآوری داده در مطالعات تحقیقاتی هستند که میتوان پاسخهای آنها را از طریق مقیاس فاصلهای سنجید یا اندازه گرفت. برای دریافت پاسخ به صورت دادههای فاصلهای، باید گزینههای مربوط به پاسخها را به متغیرهایی محدود کنیم که در آن اختلاف بین دو متغیر برابر است و میتوان به آنها مقدار عددی اختصاص دهیم.
شما احتمالاً با متغیرهایی مختلفی در یک مطالعه تحقیقاتی آشنا شدهاید که دارای این ویژگی هستند. برای مثال میزان توافق، سطح رضایت که در اکثر طرحها و پرسشنامههای نظرسنجی به کار میروند، با مقیاس اندازه گیری فاصلهای سروکار دارند. به کمک این مقیاسبندی کمی سازی دادههایی که در پرسشنامه دریافت میکنید صورت میگیرد. در ادامه به چند معیار در طرحهای تحقیق آماری مبتنی بر پرسشنامه میپردازیم که از مقیاس فاصلهای استفاده میکنند.
معیار لیکرت و مقیاس فاصله ای
یکی از روشهای مقیاسبندی پاسخهای پرسشنامهها به کمک «معیار لیکرت» (Likert Scale) صورت میپذیرد که در آن از مقیاس فاصله ای استفاده میشود. در این حالت، هر گزینه، نوع یا بخشی از احساس یا میزان را به عنوان پاسخ پرسشها نشان میدهد.
نکته: پاسخهای ۵ سطحی (یا با سطوح فرد) به صورت نااریب بوده و گزینه میانی به عنوان پاسخ بیاثر یا «خنثی» (Neutral) تلقی میشود. به نمونه زیر توجه کنید که گزینههای مربوط به میزان رضایت را نشان میدهد. گزینه «نظری ندارم» به عنوان پاسخ خنثی محسوب میشود.
- رضایت کامل.
- رضایت نسبی.
- نظری ندارم.
- ناراضی.
- کاملا ناراضی
معیار NPS و مقیاس فاصله ای
در طراحی پرسشنامههای مربوط به اندازهگیری تمایل مشتریان به معرفی محصول یا خدمات شرکت به دیگران از شاخص «امتیاز خالص مروجان» (Net Promoter Score) بهره میبرند که در آن از مقیاس فاصلهای استفاده شده است. پاسخهای محتمل برای شرکتکنندگان در طرح نظر سنجی به صورت مثلا ۱۰ گزینه ارائه میشود. سرعت و سادگی این گونه پرسشنامهها در طرحهای تحقیق بازار، موجب شده است که شرکتها و سازمانهای خدماتی از آنها به فور در روشهای اندازهگیری وفاداری مشتریان بهره ببرند.
شاخص خالص مروجان (یا به اختصار NPS) در نیمی از شرکتهای توسعه یافته به کار گرفته و نتایج از آنها استخراج و نسبت به مقادیر حاصل، تصمیمگیری میشود. در تصویر زیر یک نمونه از این معیار را مشاهده میکنید که برای تبدیل مقادیر آن به اعداد (کمی کردن) از مقیاس فاصلهای استفاده شده است.

اهمیت استفاده از مقیاسها
دانستن مقیاس اندازهگیری برای متغیرها میتواند از بروز اشتباهاتی مانند گرفتن میانگین از کدهای پستی یا گرفتن نسبت دو مقدار pH جلوگیری کند. فراتر از آن، دانستن مقیاس اندازه گیری متغیرها در برنامهریزی، تجزیه و تحلیل یا تفسیر نتایج حاصل از تکنیکهای آماری به شما کمک میکند. برای مثال میدانیم که استفاده از متغیرهای کیفی (اسمی و ترتیبی) برای طبقهبندی یا رتبهبندی مشاهدات مناسب هستند در حالیکه متغیرهای کمی (فاصلهای و نسبت) برای بدست آوردن میانگین و انحراف معیار به کار میآیند.
نکته: این موضوع را همواره به یاد داشته باشید که شاخصهای «ضریب تغییرات» (Coefficient of Variation) و خطای نسبی (Relative Error) در آمار فقط برای متغیرهای نسبت قابل محاسبه است و نباید آن را برای مقادیر اندازهگیری شده با مقیاس فاصلهای به کار برد.
توجه داشته باشید که گاهی اوقات، مقیاس اندازه گیری برای یک متغیر به طور قطع مشخص نیست یا به حوزه تحقیق وابسته است. به نظر شما رنگ باید از چه نوع مقیاسی باشد؟ در یک مطالعه روانشناختی درک، رنگهای مختلف به صورت مقیاس اسمی کدگذاری شدهاند. در یک مطالعه فیزیک، رنگ با طول موج کمی میشود، بنابراین رنگ، یک متغیر با مقیاس نسبت در نظر گرفته میشود. بنابراین حوزه کار تحقیق باید همیشه مد نظر قرار گیرد تا متغیرها به درستی به کار روند.
مواردی وجود دارد که میتوانید مقیاس اندازه گیری را کنترل کنید. به عنوان مثال، با درجه حرارت، می توانید درجه C یا F را انتخاب کنید و مقیاس فاصلهای داشته باشید یا درجه کلوین را انتخاب کنید و مقیاس نسبت را داشته باشید. یا به کمک اندازهگیری درآمد، به جای ارائه دستههای درآمدی و داشتن مقیاس ترتیبی، میتوانید درآمد واقعی را بدست آورید و مقیاس نسبت داشته باشید. به طور کلی، با مقیاس ترتیبی، امکان دستهبندی میسر شده در حالیکه با مقیاس نسبت یا فاصلهای میتوان شاخصهای آماری قابل درک و مشخص را برای درک واقعیت، محاسبه و ارائه کرد.
همانطور که دیدید، مقیاس فاصله ای این امکان را به محققین در حوزه نظر سنجی میدهد تا اطلاعات را به صورت کمی درآورده و بین گزینهها تفاوت قائل شوند تا بازخورد و پاسخها بتواند به اهداف و نتایج معنیدار ختم شوند.
خلاصه و جمعبندی
در این متن به کاربرد و ویژگیهای مقیاس فاصله ای اشاره شد و دلیل استفاده از مقیاس بندی در طرحهای جمعآوری اطلاعات نیز بیان گردید. از آنجایی که در اکثر موارد، مبنای محاسبات و اجرای تحلیلهای آماری، دادهها و اطلاعات جمعآوری (کمی و کیفی) شده است، روشی باید این دادهها را به عدد تبدیل کند. مقیاس بندی یا کدگذاری به منظور انجام این کار مورد استفاده قرار میگیرد تا همه اطلاعات به صورت عددی قابل دسترس بوده و مورد تحلیلهای مشخص آماری قرار گیرند. البته تکنیک و روشهای مختلفی برای مقیاسبندی دادهها وجود دارد که در این مجال به مقیاسبندی استیونز اشاره کردیم. در نوشتارهای بعدی از مجله فرادرس به مقیاسهای دیگر متغیرها و دادهها نیز خواهیم پرداخت.













چرا مقیاس فاصله ای میانگین داره در صورتیکه صرب و تقسیم نداره
سلام علیکم مطالب را خیلی عالی شرح دادین خدا از شما راضي باشد من خیلی استفاده کردم
باسلام و سپاس از مطالب مفید و ارزنده تان
به نظرم جای پرداختن به یک موضوع به صورت جدول خالی است.
“مشخص کزدن نوع تحلیل آماری با توجه به مقیاس اندازه کیری متغیرها”
دنبال دسته بندی منظم در این خصوص بودم که در هیچ یک از متون موجود در سایت های مختلف ندیدم.