ضریب تغییرات و خطای نسبی — به زبان ساده

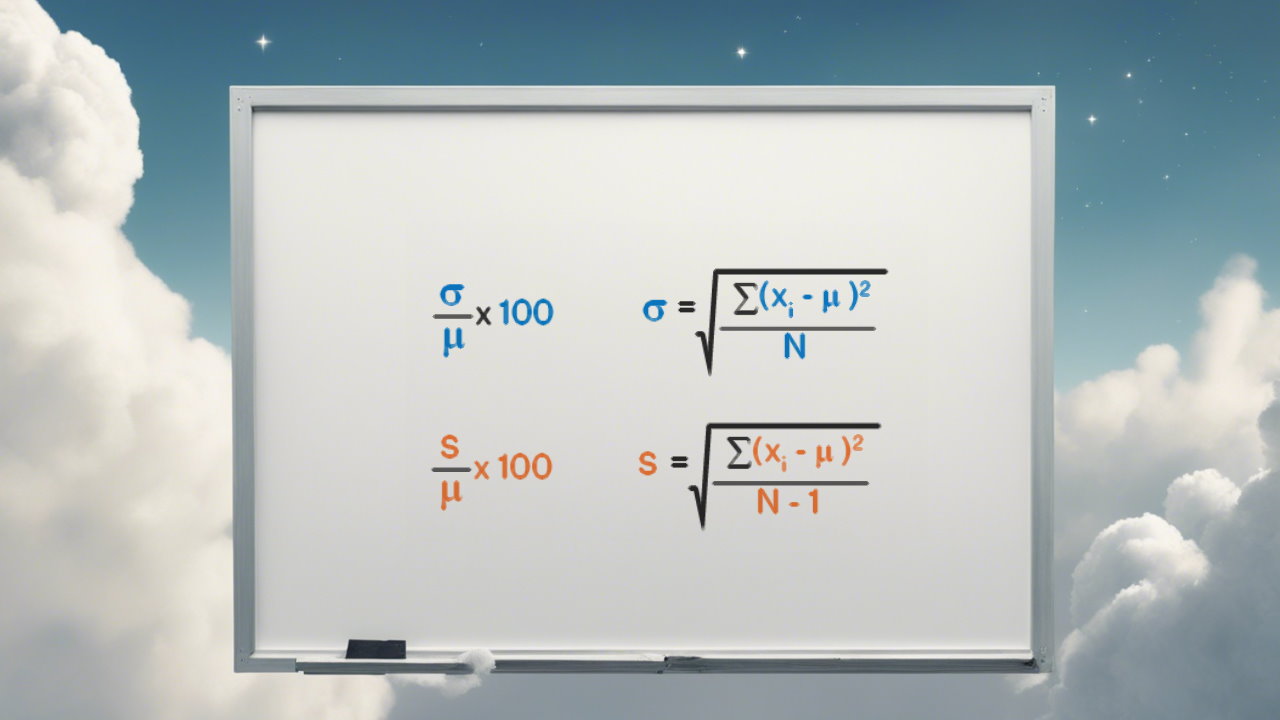
در آمار یکی از کارهایی که بیشتر اوقات صورت می‌گیرد، تخمین زدن است. معمولا میانگین نمونه‌ای را به عنوان برآوردی از میانگین جامعه در نظر می‌گیریم. به این ترتیب پارامتر جامعه را بوسیله نمونه مشخص می‌کنیم. البته می‌دانیم که این کار همیشه با مقداری خطا همراه است که با توجه به نمونه گرفته شده، مقدار این خطا قابل اندازه‌گیری است. در نوشتارهای دیگری از مجله فرادرس با مفهوم ضریب تغییرات و خطای نسبی آشنا شده‌اید. در اینجا هم می‌‌خواهیم بین این دو اصطلاح یک پیوند برقرار کنیم و مشخص کنیم آنچه که بوسیله ضریب تغییرات اندازه‌گیری می‌شود همان خطای نسبی مشاهدات برای برآورد میانگین است.

به منظور آشنایی بیشتر با مفاهیم و اصطلاحات به کار رفته در این نوشتار، بهتر است مطالب واریانس و اندازه‌های پراکندگی — به زبان ساده و خطای اندازه گیری — به زبان ساده را مطالعه کنید. همچنین خواندن نوشتارهای ضریب تغییرات در SPSS — راهنمای کاربردی و دقت و صحت اندازه گیری – به زبان ساده نیز خالی از لطف نیست.

ضریب تغییرات و خطای نسبی

یکی از شاخص‌های آمار توصیفی که اغلب برای نمایش و مقایسه میزان پراکندگی بین دو جامعه یا دو متغیر به کار می‌رود، «ضریب تغییرات» (Coefficient of Variation) است. از آنجایی که کم بودن پراکندگی، نشانگر همگن بودن جامعه است، هر چه میزان ضریب تغییرات کمتر باشد، میانگین را معیار بهتری برای نقطه تمرکز می‌یابیم.

فیلم آموزش آمار و احتمال مهندسی – جامع و با مثال های مختلف در فرادرس

کلیک کنید

بنابراین در بین دو جامعه، آن که دارای ضریب تغییرات کمتری باشد، جامعه بهتری بوده، زیرا نتایج گرفته شده از شاخص میانگین، دقت بیشتری دارند. از آنجایی که ضریب تغییرات بوسیله یک نسبت از کمیت‌های هم واحد، محاسبه و ساخته می‌شود، هیچ واحد اندازه‌گیری نداشته و به صورت درصدی مورد استفاده قرار می‌گیرد. همین موضوع نیز اهمیت استفاده از این شاخص را برای مقایسه بین جوامع مختلف، مشخص می‌کند.

از طرفی برای محاسبه یا تخمین خطا نیز روش‌های گوناگونی وجود دارد. برای مثال می‌توان به «خطای مطلق» (Absolute Error) و «خطای نسبی» (Relative Error) اشاره کرد که هر یک به شیوه‌های متفاوت، خطای یک تخمین برای یک مقدار مشخص را تعیین می‌کنند.

محاسبه ضریب تغییرات

معیارها و شاخص‌های مختلفی برای اندازه‌گیری پراکندگی داده‌ها وجود دارد. برای مثال «دامنه تغییرات» (Range) یک معیار ساده بوده که حداکثر میزان پراکندگی را نشان می‌دهد. ولی به نظر می‌رسد بعضی خصوصیات و ويژگی‌های خاصی که یک شاخص پراکندگی باید داشته باشد، در دامنه تغییرات وجود ندارد. چند نمونه از این خصوصیات در ادامه ذکر شده‌اند.

• شاخص پراکندگی باید به کمک یک عدد، میزان پراکندگی را نمایش دهد.
• شاخص پراکندگی باید فاصله یا دوری داده‌ها را اندازه‌گیری کند.
• شاخص پراکندگی باید فاصله یا دوری را نسب به یک نقطه مرکزی محاسبه کند.
• شاخص پراکندگی باید با تغییر مقیاس داده‌ها تغییر نکند.

همانطور که می‌دانید، شاخص‌های مختلفی برای اندازه‌گیری پراکندگی معرفی شده‌اند. دامنه تغییرات، میانگین قدرمطلق فاصله از میانگین، میانگین قدرمطلق فاصله از میانه، واریانس (Variance)، انحراف معیار (Standard Deviation) و ضریب تغییرات در این گروه از شاخص‌های آمار توصیفی (Descriptive Statistics) قرار گرفته‌اند.

فیلم آموزش آمار و احتمالات مهندسی – حل نمونه سوالات کنکور ارشد در فرادرس

کلیک کنید

به غیر از دامنه تغییرات، بقیه شاخص‌ها، نقطه‌ای را به عنوان معیار تمرکز در نظر گرفته و پراکندگی را حول آن اندازه‌گیری می‌کنند ولی دامنه تغییرات حداکثر فاصله را محاسبه می‌کند. جدول ۱، به بررسی خصوصیات هر یک از این شاخص‌ها پرداخته است.

جدول ۱: مقایسه ویژگی‌های شاخص‌های پراکندگی

همانطور که در جدول ۱ دیده می‌شود، به جز ضریب تغییرات، شاخص‌های پراکندگی دیگر، به مقیاس اندازه‌گیری داده‌ها وابستگی دارند در نتیجه برای مقایسه معیار پراکندگی بین دو یا چند جامعه مناسب نیستند.

به یاد دارید که میانگین ($$\bar{X}$$) و واریانس (Var)، همینطور انحراف معیار (SD) بوسیله رابطه‌های زیر محاسبه می‌شوند.

$$\large \bar{X} = \dfrac{\sum_{i=1}^n X_i } {n}$$

$$\large Var = \dfrac{\sum_{i=1}^n (X_i - \bar{X} ) ^2}{n}$$

$$\large SD = \sqrt{Var}$$

نکته: اغلب برای نمایش فرمول و رابطه محاسباتی ضریب تغییرات از علامت $$\mu$$ به عنوان میانگین و $$S$$ برای انحراف معیار استفاده می‌کنند. در نتیجه محاسبه ضریب تغییرات به شکل زیر خواهد بود.

$$\large CV = \dfrac{S}{\mu}$$

رابطه ۱

محاسبه خطای نسبی

فرض کنید مقدار $$\bar{X}$$ هدف تخمین باشد. به این منظور یک نمونه تصادفی در نظر گرفته‌ایم و می‌خواهیم بوسیله مشاهدات حاصل از آن، میانگین را تخمین بزنیم. هر یک از مقادیر مشاهده شده نسبت به مقدار واقعی که میانگین جامعه است، خطا یا اختلافی دارند.

گام اول برای محاسبه خطای نسبی، بدست آوردن خطای مطلق است. در نتیجه خطای مطلق برای هر یک از مشاهدات به صورت زیر محاسبه می‌شود. فرض کنید خطای مطلق را برای مشاهده $$i$$ام به صورت $$e_i$$ مشخص کرده‌ایم.

$$\large e_i = X_i - \bar{X}$$

رابطه ۲

نکته: اغلب برای اندازه‌گیری خطا، از قدر مطلق فاصله استفاده می‌کنند زیرا جهت خطا مهم نبوده و فقط میزان خطا از اهمیت برخوردار است. ما این کار را در گام بعدی انجام خواهیم داد.

در گام دوم با تقسیم مقدار خطای مطلق بر مقدار هدف، خطای نسبی را بدست می‌آوریم. در اینجا خطای نسبی برای مشاهده $$i$$ام را با $$R_i$$ نشان خواهیم داد.

$$\large R_i = \dfrac{ e_i} {\bar{X}}$$

رابطه ۳

گام سوم، نمایش مقدار مثبت این نسبت در رابطه ۳، است. با استفاده از قدر مطلق، می‌توان این عمل را انجام داد. ولی به علت خاصی ما از تابع مربع یا توان ۲ استفاده می‌کنیم. در نتیجه خطای نسبی (با مقدار مثبت) را به صورت زیر محاسبه می‌کنیم.

$$\large R_i^2 = \left(\dfrac{ e_i} {\bar{X}}\right)^2$$

رابطه ۴

تا اینجا، محاسبه صورت گرفته در رابطه ۴، همان خطای نسبی است که به توان ۲ رسیده است. ولی در قسمت بعدی نشان می‌دهیم که جذر این نسبت همان ضریب تغییرات است. بنابراین ضریب تغییرات و خطای نسبی هر دو ماهیت و شکل یکسانی دارند. به این ترتیب نشان می‌دهیم که ضریب تغییرات، میزان خطای نسبی مشاهدات برای میانگین‌شان است.

تفسیر ضریب تغییرات و خطای نسبی

در این قسمت رابطه ۴ را تبدیل به ضریب تغییرات معرفی شده در رابطه ۱ خواهیم کرد. طرف راست رابطه ۴ را در نظر بگیرید. با جایگزینی $$e_i$$ با مقداری که در رابطه ۲ معرفی شده، کار را ادامه می‌دهیم.

$$\large \left(\dfrac{ e_i} {\bar{X}}\right)^2 = \left(\dfrac{X_i - \bar{X}}{\bar{X}}\right)^2$$

فیلم آموزش آمار و احتمال مهندسی – حل تمرین و تست کنکور ارشد در فرادرس

کلیک کنید

حال مخرج را به توان ۲ رسانده و جداگانه نمایش می‌دهیم.

$$\large \dfrac{1}{\bar{X}^2} \left( X_i\right)^2$$

از آنجا که محاسبه صورت گرفته، فقط برای یک مشاهده است با جمع‌بندی روی همه مشاهدات، یک عدد و شاخص برای کل نمونه تصادفی ایجاد می‌کنیم.

$$\large \dfrac{1}{ \bar{ X }^2} \sum_{i = 1}^n \left( X_i - \bar{ X } \right)^2$$

در انتها نیز از میانگین‌گیری برای جمع‌بندی استفاده می‌کنیم.

$$\large \dfrac{1}{ \bar{ X }^2} \sum_{i = 1}^n \dfrac{\left( X_i - \bar{X} \right)^2 }{n}$$

حال اگر از این عبارت جذر بگیریم، به مقدار $$CV$$ خواهیم رسید.

$$\large CV = \dfrac{\sum_{i = 1}^n \left( X_i - \bar{X}\right)^2/n}{\bar{X}} \simeq \dfrac{S}{\mu}$$

در نتیجه ضریب تغییرات جذر، میانگین مربعات خطای نسبی مشاهدات برای میانگین‌شان خواهد بود. از طرفی می‌دانیم که خطای نسبی، به واحد اندازه‌گیری مقادیر وابسته نیست. به همین دلیل هم ضریب تغییرات به صورت درصدی و بدون حساسیت نسبت به واحد اندازه‌گیری است. همین ویژگی باعث می‌شود که برای مقایسه پراکندگی بین دو جامعه از این شاخص آماری استفاده شود.

خلاصه و جمع‌بندی

در این نوشتار روش محاسبه ضریب تغییرات و خطای نسبی مرور و نقاط مشترک آن‌ها مشخص شد. به سادگی می‌توان دید که ضریب تغییرات همان خطای نسبی مشاهدات برای برآورد میانگین است. بنابراین اگر میانگین را مبدا یا مرکز داده‌ها در نظر بگیریم، ضریب تغییرات، خطای نسبی را برای یک نمونه تصادفی به منظور برآورد میانگین نشان می‌دهد. مشخص است که فرمول محاسباتی ضریب تغییرات نیز همین موضوع را نشان داده و مشخص می‌کند به ازاء هر واحد تغییر در میانگین، به چه میزان یا نسبت واریانس یا انحراف معیار تغییر خواهند کرد.