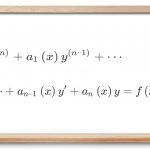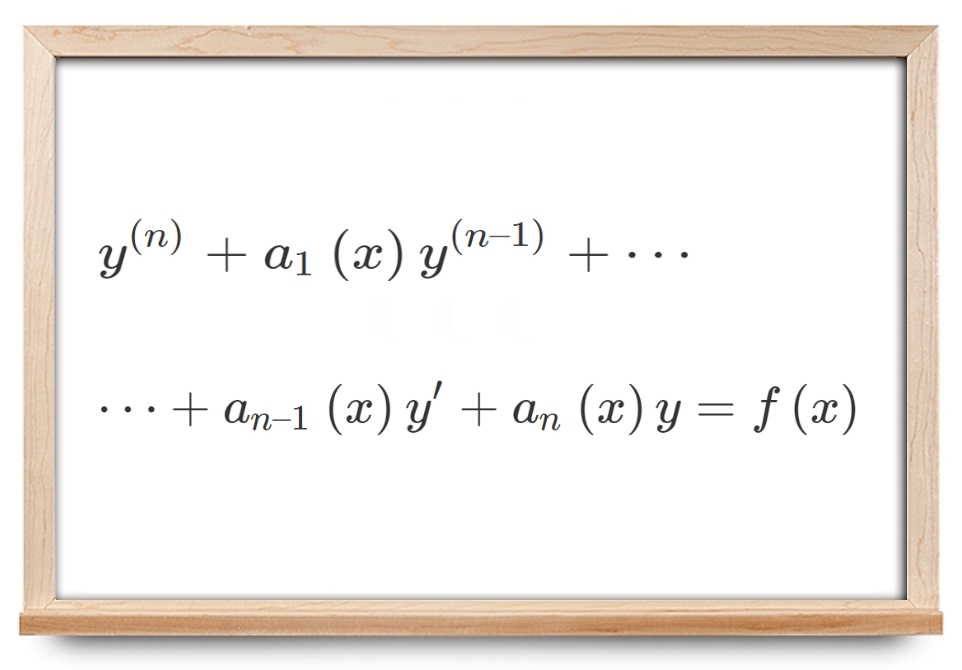معادلات دیفرانسیل ناهمگن مرتبه بالا با ضرایب متغیر – به زبان ساده

در آموزش‌های قبلی از مجموعه مطالب ریاضیات مجله فرادرس، با معادلات دیفرانسیل آشنا شدیم. در این آموزش‌ها، روش‌های حل معادلات دیفرانسیل مرتبه اول، معادلات دیفرانسیل مرتبه دوم و معادلات مرتبه بالاتر را معرفی کردیم. همچنین، با نوع خاصی از معادلات دیفرانسیل مرتبه بالا، یعنی معادلات دیفرانسیل همگن مرتبه بالا با ضرایب متغیر آشنا شدیم. در این آموزش، معادلات ناهمگن مرتبه بالا با ضرایب متغیر را بیان می‌کنیم.

معادلات ناهمگن مرتبه بالا با ضرایب متغیر

معادله‌ای به فرم زیر را معادله دیفرانسیل مرتبه بالای ناهمگن با ضرایب متغیر می‌نامند:

$$\large { { y ^ { \left ( n \right ) } } + { a _ 1 } \left ( x \right ){ y ^ { \left ( { n – 1 } \right ) } } + \cdots } + { { a _ { n – 1 } } \left ( x \right ) y ^ \prime }+{ { a _ n } \left ( x \right ) y } = { f \left ( x \right ) }$$

که در آن، $$a_1(x)$$، $$a_2(x)$$، ... و $$a_n(x)$$ توابعی پیوسته در بازه $$\left[ {a,b} \right]$$ هستند.

با استفاده از عملگر دیفرانسیلی خطی $$L$$، معادله بالا را می‌توان به شکل فشرده زیر نوشت:

$$\large L y \left ( x \right ) = f \left ( x \right )$$

که در آن، $$L$$ شامل حاصل‌ضرب عملگرهای دیفرانسیلی و ضرایب $${a_i}\left( x \right)$$ است.

همان‌طور که می‌دانیم، جواب عمومی $$y (t )$$ یک معادله دیفرانسیل ناهمگن، برابر با مجموع جواب عمومی $$y _ 0 (t)$$ معادله همگن متناظر و یک جواب خصوصی $$y _ 1 (t )$$ معادله ناهمگن است:

$$\large y \left ( x \right ) = { y _ 0 } \left ( x \right ) + { y _ 1 } \left ( x \right ) .$$

قبلاً روش‌های یافتن جواب عمومی معادلات مرتبه بالای همگن را معرفی کردیم. بنابراین، در اینجا بر یافتن جواب معادلات ناهمگن تمرکز می‌کنیم. بدین منظور، از روش تغییر ثوابت که به نام روش لاگرانژ نیز شناخته می‌شود، استفاده می‌کنیم. اگر جواب عمومی معادله همگن را بدانیم، با استفاده از این روش می‌توانیم جواب عمومی معادله ناهمگن را نیز به دست آوریم.

روش تغییر ثوابت

فرض کنید می‌خواهیم معادله دیفرانسیل ناهمگن مرتبه $$n$$ زیر را حل کنیم:‌

$$\large { { y ^ { \left ( n \right ) } } + { a _ 1 } \left ( x \right ){ y ^ { \left ( { n – 1 } \right ) } } + \cdots } + { { a _ { n – 1 } } \left ( x \right ) y ’ } + { { a _ n } \left ( x \right ) y } = { f \left ( x \right ) . }$$

فیلم آموزش معادلات دیفرانسیل با رویکرد حل مساله و تست کنکور ارشد در فرادرس

کلیک کنید

فرض می‌کنیم جواب عمومی معادله همگن متناظر به صورت زیر باشد:

$$\large { { y _ 0 } \left ( x \right ) = { C _ 1 } { Y _ 1 } \left ( x \right ) } + { { C _ 2 } { Y _ 2 } \left ( x \right ) + \cdots } + { { C _ n } { Y _ n } \left ( x \right ) }$$

که تعداد $$n$$ ثابت $$C_1$$، $$C_2$$، $$\ldots$$ و $$C_n$$ اختیاری دارد.

ایده این روش، جایگزینی ثابت‌های $$C_1$$، $$C_2$$، ... و $$C_n$$ با تابع‌های مشتق‌پذیر پیوسته $$C_1 (x)$$، $$C_2 (x)$$، ... و $$C_n (x)$$ است؛ به طوری که جواب زیر در معادله دیفرانسیل ناهمگن صدق کند:

$$\large \begin {align*} y \left ( x \right ) & = { { C _ 1 } \left ( x \right ) { Y _ 1 } \left ( x \right ) } + { { C _ 2 } \left ( x \right ) { Y _ 2 } \left ( x \right ) + \cdots } + { { C _ n } \left ( x \right ) { Y _ n } \left ( x \right ) } \\ & = { \sum \limits _ { i = 1 } ^ n { { C _ i } \left ( x \right ){ Y _ i } \left ( x \right ) } } \end {align*}$$

مشتق اول توابع $$C_i (x)$$ را می‌توان از دستگاه $$n$$ معادله‌ای زیر تعیین کرد:

$$\large \left \{ \begin {array} {l} { { C ’ _ 1 } \left ( x \right ) { Y _ 1 } \left ( x \right ) } + { { C ’ _ 2 } \left ( x \right ) { Y _ 2 } \left ( x \right ) + \cdots } + { { C ’ _ n } \left ( x \right ) { Y _ n } \left ( x \right ) } = { 0 } \\ { { C ’ _ 1 } \left ( x \right ) { Y ’ _ 1 } \left ( x \right ) } + { { C ’ _ 2 } \left ( x \right ) { Y ’ _ 2 } \left ( x \right ) + \cdots } + { { C ’ _ n } \left ( x \right ) { Y ’ _ n } \left ( x \right ) } = { 0 } \\ \cdots \cdots \cdots \cdots \cdots \cdots \cdots \\ { {C ’_ 1} \left ( x \right ) Y _ 1 ^ { \left ( { n – 1 } \right ) } \left ( x \right ) } + { { C ’ _ 2 } \left ( x \right ) Y _ 2 ^ { \left ( { n – 1 } \right ) } \left ( x \right ) + \cdots } + { { C ’ _ n } \left ( x \right ) Y _ n ^ { \left ( { n – 1 } \right ) } \left ( x \right ) } = { f \left ( x \right ) } \end{array} \right .$$

دترمینان اصلی این دستگاه، رونسکین $$W (x)$$ است که از دستگاه اساسی جواب‌های $$Y_1$$، $$Y_2$$، ... و $$Y_n$$ تشکیل شده است. از آنجایی که جواب‌های $$Y_1$$، $$Y_2$$، ... و $$Y_n$$ مستقل خطی هستند، رونسکین صفر نیست.

مشتق‌های مجهول $${C’_i}\left( x \right)$$ با استفاده از قاعده کرامر به دست می‌آیند:

$$\large { { C ’ _ i } \left ( x \right ) = \frac { { { W _ i } \left ( x \right ) } } { { W \left ( x \right ) } } , \; \; } \kern-0.3pt { i = 1 , 2 , \ldots , n }$$

که در آن، دترمینان $${{W_i}\left( x \right)}$$ از رونسکین $$W(x)$$ و با جایگزینی ستون $$i$$اُم با ستون $$\left[ {0,0, \ldots, f\left( x \right)} \right] ^ T$$ سمت راست به دست می‌آید.

علاوه بر این، توصیف $${C_i}\left( x \right)$$ را می‌توان با انتگرال زیر تعیین کرد:

$$\large { { C _ i } \left ( x \right ) } = { \int { \frac { { { W _ i } \left ( x \right ) } } { { W \left ( x \right ) } } d x } + { A _ i } , \; \; } \kern-0.3pt { i = 1 , 2 , \ldots , n . }$$

در فرمول بالا، $${A_i}$$ ثابت انتگرال‌گیری است.

در نتیجه، جواب عمومی معادله ناهمگن را می‌توان به صورت زیر نوشت:

$$\large \begin {align*} y \left ( x \right ) & = { \sum \limits _ { i = 1 } ^ n { { C _ i } \left ( x \right ) { Y _ i } \left ( x \right ) } } \\ & = { \sum \limits _ { i = 1 } ^ n { \left ( { \int { \frac { { { W _ i } \left ( x \right ) } } { { W \left ( x \right ) } } d x } + { A _ i } } \right ) { Y _ i } \left ( x \right ) } } \\ & = { \sum \limits _ { i = 1 } ^ n { { A _ i } { Y _ i } \left ( x \right ) } } + { \sum \limits _ { i = 1 } ^ n { \left ( { \int { \frac { { { W _ i } \left ( x \right ) } } { { W \left ( x \right ) } } d x } } \right ){ Y _ i } \left ( x \right ) } } \\ & = { { y _ 0 } \left ( x \right ) + { y _ 1 } \left ( x \right ) . } \end {align*}$$

در عبارت بالا، مجموع یا سیگمای اول، مربوط به جواب عمومی $$y _0 (x)$$ معادله همگن (با اعداد دلخواه $$A_i$$) است و مجموع دوم، جواب خصوصی $$y_1(x)$$ معادله ناهمگن را توصیف می‌کند.

مثال

جواب عمومی معادله دیفرانسیل زیر را به دست آورید.

$$\large { \left ( { { x ^ 2 } – 2 } \right ) y ^ { \prime \prime \prime } } - { 2 x y ^ { \prime \prime } } - { \left ( { { x ^ 2 } – 2 } \right ) y ’ } + { 2 x y } = { 2 x – \frac { 4 } { y } . }$$

حل: ابتدا جواب عمومی معادله همگن را محاسبه می‌کنیم:‌

$$\large { \left ( { { x ^ 2 } – 2 } \right ) y ^ { \prime \prime \prime } } - { 2 x y ^ { \prime \prime } } - { \left ( { { x ^ 2 } – 2 } \right ) y ’ } + { 2 x y } = { 0 . }$$

از تقارن معادله استفاده کرده و متغیر جدید زیر را معرفی می‌کنیم:

$$\large v = y ^ { \prime \prime } – y .$$

در نتیجه، معادله به صورت زیر در می‌آید:‌

$$\large \left ( { { x ^ 2 } – 2 } \right ) v ’ – 2 x v = 0 .$$

معادله اخیر را می‌توان به سادگی و با استفاده از جداسازی متغیرها حل کرد:

$$\large \begin {align*} & \left ( { { x ^ 2 } – 2 } \right ) \frac { { d v } } { { d x } } = 2 x v , \; \; \Rightarrow { \frac { { d v } } { v } = \frac { { 2 x d x} } { { { x ^ 2 } – 2 } } , \; \; } \\ & \Rightarrow { \int { \frac { { d v } } { v } } = \int { \frac { { 2 x d x } }{ { { x ^ 2 } – 2 } } } , \; \; } \Rightarrow { \int { \frac { { d v } } { v } } = \int { \frac { { d \left ( { { x ^ 2 } – 2 } \right ) } } { { { x ^ 2 } – 2 } } } , \; \; } \\ & \Rightarrow { { \ln \left | v \right | = \ln \left | { { x ^ 2 } – 2 } \right | } +{ \ln { B _ 1 } \; \left ( { { B _ 1 } \gt 0 } \right ) , \; \; } } \\ & \Rightarrow { \ln \left | v \right | = \ln \left ( { { B _ 1 } \left | { { x ^ 2 } – 2 } \right | } \right ) , \; \; } \Rightarrow { \left | v \right | = { B _ 1 } \left | { { x ^ 2 } – 2 } \right | , \; \; } \\ & \Rightarrow { v = { B _ 2 } \left ( { { x ^ 2 } – 2 } \right ) } \end {align*}$$

که در آن، $$B_2$$ یک عدد دلخواه است.

اکنون تابع $$y (x)$$ را محاسبه می‌کنیم:

 $$\large { y ^ { \prime \prime } – y = v , \; \; } \Rightarrow { y ^ { \prime \prime } – y } = { { B _ 2 } \left ( { { x ^ 2 } – 2 } \right ) . }$$

معادله بالا، یک معادله ناهمگن مرتبه دوم است. حل معادله همگن متناظر با معادله بالا، به صورت زیر است:

$$\large { y ^ { \prime \prime } – y = 0 , \; \; } \Rightarrow { { \lambda ^ 2 } – 1 = 0 , \; \; } \\ \large \Rightarrow { { \lambda _ { 1 , 2 } } = \pm 1 , \; \; } \Rightarrow { { y _ 0 } \left ( x \right ) = { C _ 1 } {e ^ x } + { C _ 2 } { e ^ { – x } } . }$$

سمت راست معادله ناهمگن، یعنی $${B_2}\left( {{x^2} – 2} \right)$$، یک چندجمله‌ای مربعی است. بنابراین، یک جواب خصوصی برای معادله ناهمگن به صورت زیر خواهد بود:

$$\large { y _ 1 } = D { x ^ 2 } + E x + F .$$

مشتق اول و دوم این جواب برابر است با:

$$\large { { y ’ _ 1 } = 2 D x + E , \,\, \, \, \; \; } \kern-0.3pt { { y ^ { \prime \prime } _ 1 } = 2 D }$$

با قرار دادن تابع و مشتق دوم آن در معادله دیفرانسیل ناهمگن، به معادلات زیر برای ضرایب $$D$$، $$E$$ و $$F$$ می‌رسیم:

$$\large { { 2 D – \left ( { D { x ^ 2 } + E x + F } \right ) } = { { B _2 } { x ^ 2 } – 2 { B _ 2 } , \; \; } } \\ \large \Rightarrow { { 2 D – D { x ^ 2 } – E x – F } = { { B _ 2 } { x ^ 2 } – 2 { B _ 2 } . } }$$

در نتیجه، داریم:

$$\large { \left\{ \begin {array} {l} – D = { B _ 2 } \\ – E = 0 \\ 2 D – F = – 2 { B _ 2 } \end {array} \right . , \; \; } \Rightarrow { \left \{ \begin {array} {l} D = – { B _ 2 } \\ E = 0 \\ F = 0 \end{array} \right..}$$

بنابراین، جواب خصوصی $$y _1$$‌ به صورت زیر خواهد بود:

 $$\large { y _ 1 } = – { B _ 2 } { x ^ 2 } .$$

در تابع بالا، به جای عدد دلخواه $$-B_2$$ ثابت $$C_3$$ را قرار می‌دهیم. در نهایت، جواب عمومی معادله همگن برابر است با:‌

$$\large { { y _ 0 } \left ( x \right ) } = { { C _ 1 } { e ^ x } } + { { C _ 2 } { e ^ { – x } } } + { { C _ 3 } { x ^ 2 } . }$$

در جواب بالا، توابع $${Y_1} = {e^x}$$، $${Y_2} = {e^{ – x}}$$ و $${Y_3} = {x^2}$$ یک دستگاه اساسی از جواب‌ها را تشکیل می‌دهند.

اکنون جواب معادله ناهمگن را با استفاده از روش تغییر ثوابت به دست می‌آوریم. جواب عمومی به فرم زیر است:‌

‍$$\large { y \left ( x \right ) } = { { C _ 1 } \left ( x \right ) { e ^ x } } + { { C _ 2 } \left ( x \right ) { e ^ { – x } } } + { {C _ 3 } \left ( x \right ) { x ^ 2 } }$$

که در آن، مشتقات توابع مجهول $$C_1 (x)$$، $$C_2 (x)$$ و $$C_3 (x)$$ در دستگاه معادلات زیر صدق می‌کنند:

$$\large \left\{ \begin {array} {l} { { C ’ _ 1 } { e ^ x } + { C ’ _ 2 } { e ^ { – x } } } + { { C ’ _ 3 } { x ^ 2 } } = { 0 } \\ { { C ’ _ 1 } { e ^ x } – { C ’ _ 2 } { e ^ { – x } } } + { 2 { C ’ _ 3 } x } = { 0 } \\ { { C ’ _ 1 } { e ^ x } + { C ’ _ 2 } { e ^ { – x } } } + { 2 { C ’ _ 3 } } = { 2 x – \frac { 4 } { x } } \end {array} \right.$$

حال دترمینان دستگاه معادلات را محاسبه می‌کنیم:

$$ \large \begin {align*} \require{cancel}<br /> W & \text { = } \kern0pt { \left | { \begin {array} { * { 2 0 } {c } }<br /> { { e ^ x } } & { { e ^ { – x } } } & { { x^ 2 } } \\<br /> { { e ^ x } } & { – { e ^ { – x } } } & { 2 x } \\<br /> { { e ^ x } } & { { e ^ { – x } } } & 2<br /> \end {array} } \right | }<br /> = { { e ^ x } { e ^ { – x } } \left | { \begin {array} { * { 2 0 } { c } }<br /> 1 & 1 & { { x ^ 2 } } \\<br /> 1 & { – 1 } & { 2 x } \\<br /> 1 & 1 & 2<br /> \end{array} } \right | } \\<br /> & = { { 1 \cdot \left [ { 1 \left ( { – 2 – 2 x } \right ) } \right . } - { \left . { 1 \left ( { 2 – { x ^ 2 } } \right ) } \right . } } + { { \left . { 1 \left ( { 2 x + { x ^ 2 } } \right ) } \right ] } } \\<br /> & = { – 2 – \cancel { 2 x } – 2 } + { { x ^ 2 } + \cancel { 2 x } + { x ^ 2 } }<br /> = { 2 { x ^ 2 } – 4 } \end {align*} $$

$$ \large \begin {align*} \require {cancel}<br /> { W _ 1} & = \kern0pt { \left | { \begin {array} { * { 2 0 } {c } }<br /> 0 & { { e ^ { – x } }} & { { x ^ 2 } } \\<br /> 0 & { – { e ^ { – x } } } & { 2 x } \\<br /> { 2 x – \frac { 4 } { x } } & { { e ^ { – x } } } & 2<br /> \end {array} } \right | }<br /> = { { \left ( { 2 x – \frac { x } { 4 } } \right ) \cdot } \kern0pt { \left ( { 2 x { e ^ { – x } } + { x ^ 2 } { e ^ { – x } } } \right ) } } \\<br /> & = { \left ( { 2 { x ^ 2 } – 4 } \right ) \left ( { x + 2 } \right ) { e ^ { – x } } } \end {align*} $$

$$ \large \begin {align*} \require {cancel}<br /> { W _ 2 } & = \kern0pt { \left | { \begin {array} { * { 2 0 } {c } }<br /> { { e ^ x } } & 0 & { { x ^ 2 } } \\<br /> { { e ^ x } } & 0 & { 2 x } \\<br /> { { e ^ x } } & { 2 x – \frac { 4 } { x } } & 2<br /> \end {array} } \right | }<br /> = { { – \left ( { 2 x – \frac { x } { 4 } } \right ) \cdot } \kern0pt { \left ( { 2 x { e ^ x } – { x ^ 2 } { e ^ x } } \right ) } } \\<br /> & = { \left ( { 2 { x ^ 2 } – 4 } \right ) \left ( { x – 2 } \right ) { e ^ x } }<br /> \end {align*} $$

$$ \large \begin {align*} \require {cancel}<br /> { W _ 3 } & = \kern0pt { \left | { \begin {array} { * { 2 0 } { c } }<br /> { { e ^ x } } & { { e ^ { – x } } } & 0 \\<br /> { { e ^ x } } & { – { e ^ { – x } } } & 0 \\<br /> { { e ^ x } } & { { e ^ { – x } } } & { 2 x – \frac { 4 } { x } }<br /> \end {array} } \right | }<br /> = { { e ^ { – x } } { e ^ x } \left | { \begin {array} { * { 2 0 } { c } }<br /> 1 & 1 & 0 \\<br /> 1 & { – 1 } & 0 \\<br /> 1 & 1 & { 2 x – \frac { 4 } { x } }<br /> \end {array} } \right | } \\<br /> & = { \left ( { 2 x – \frac { x } { 4 } } \right ) \left ( { – 1 – 1 } \right ) }<br /> = { – \frac { 2 } { x } \left ( { 2 { x ^ 2 } – 4 } \right ) . }<br /> \end {align*} $$

بنابراین، حاصل $${C’_1}$$، $${C’_2}$$ و $${C’_3}$$ به صورت زیر است:‌

$$\large \begin {align*} C ’ _ 1 & = \frac { { { W _ 1 } } } { W } = { \frac { { \cancel { \left ( { 2 { x ^ 2 } – 4 } \right ) } \left ( { x + 2 } \right ) { e ^ { – x } } } } { \cancel { 2 { x ^ 2 } – 4 } } } = { \left ( { x + 2 } \right ) { e ^ { – x } } ,} \\ C ’ _ 2 & = \frac { { { W _ 2 } } } { W } = { \frac { { \cancel { \left ( { 2 { x ^ 2 } – 4 } \right ) } \left ( { x – 2 } \right ) { e ^ {x } } } } { \cancel{ 2 { x ^ 2 } – 4 } } } = { \left ( { x – 2 } \right ) { e ^ { x } } , } \\ C ’ _ 3 & = \frac { { { W _ 3 } } } { W } = { \frac { { – \frac { 2 } { x } \cancel { \left ( { 2 { x ^ 2 } – 4 } \right ) } } } { \cancel { 2 { x ^ 2 } – 4 } } } = { – \frac { 2 } { x } . } \end {align*}$$

با انتگرال‌گیری از توابع بالا، $$C_1(x)$$، $$C_2 (x)$$ و $$C_3 (x)$$ به دست می‌آیند:

$$ \large \begin {align*} \require {cancel}<br /> { { C _ 1 } \left ( x \right ) } & = { \int { \left ( { x + 2 } \right ) { e ^ { – x } } d x } }<br /> = { \left [ { \begin {array} { * { 2 0 } { l } }<br /> { u = x + 2 } \\<br /> { v ’ = { e ^ { – x } } } \\<br /> { u ’ = 1 } \\<br /> { v = – { e ^ { – x } } }<br /> \end {array} } \right ] } \\<br /> & = { – \left ( { x + 2 } \right ) { e ^ { – x } } – \int { \left ( { – { e ^ { – x } } } \right ) d x } }<br /> = { – \left ( { x + 2 } \right ) { e ^ { – x } } + \int { { e ^ { – x } } d x } }<br /> \\ & = { – \left ( { x + 2 } \right ) { e ^ { – x } } – { e ^ { – x } } + { A _ 1 } }<br /> = { – \left ( { x + 3 } \right ) { e ^ { – x } } + { A _ 1 } }<br /> \end {align*} $$

$$ \large \begin {align*}<br /> C _ 2 \left ( x \right ) & = { \int { \left ( { x – 2 } \right ) { e ^ x } d x } }<br /> = { \left [ { \begin {array} { * { 2 0 } { l } }<br /> { u = x – 2 } \\<br /> { v ’ = { e ^ x } } \\<br /> { u ’ = 1 } \\<br /> { v = { e ^ x } }<br /> \end {array} } \right ] } \\<br /> & = { \left ( { x – 2 } \right ) { e ^ x } – \int { { e ^ x } d x } }<br /> = { \left ( { x – 2 } \right ) { e ^ x } – { e ^ x } + { A _ 2 } }<br /> \\ &= { \left ( { x – 3 } \right ) { e ^ x } + { A _ 2 } , }<br /> \end {align*} $$

$$\large \begin {align*} C _ 3 \left ( x \right ) & = { \int { \left ( { – \frac { 2 } { x } } \right ) d x } } \\ & = { – 2 \int { \frac { { d x } } { x } } } = { – 2 \ln \left | x \right | + { A _ 3 } . } \end {align*}$$

در نتیجه، جواب عمومی معادله ناهمگن به صورت زیر خواهد بود:

$$ \large \begin {align*} \require {cancel}<br /> { y \left ( x \right ) }<br /> & = { { { C _ 1 } \left ( x \right ) { Y _ 1 } \left ( x \right ) } + { { C _ 2 } \left ( x \right ) { Y _ 2 } \left ( x \right ) } } + { { { C _ 3 } \left ( x \right ) { Y _ 3 } \left ( x \right ) } } \\<br /> & = { \left [ { – \left ( { x + 3 } \right ) { e ^ { – x } } + { A _ 1 } } \right ] { e ^ x } }<br /> + { \left [ { \left ( { x – 3 } \right ) { e ^ x } + { A _ 2 } } \right ] { e ^ { – x } } }<br /> + { \left [ { – 2 \ln \left | x \right | + { A _ 3 } } \right ] { x ^ 2 } } \\<br /> & = { { A _ 1 } { e ^ x } + { A _ 2 } { e ^ { – x } } + { A _ 3 } { x ^ 2 } }<br /> – { \left ( { x + 3 } \right ) + x } - { 3 – 2 { x ^ 2 } \ln \left | x \right | }<br /> \\ & = { { A _ 1 } { e ^ x } + { A _ 2 } { e ^ { – x } } + { A _ 3 } { x ^ 2 } } - { 2 { x ^ 2 } \ln \left | x \right | – 6. }<br /> \end {align*} $$

اگر این مطلب برایتان مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• آموزش معادلات دیفرانسیل با رویکرد حل مساله و تست کنکور ارشد
• معادله دیفرانسیل برنولی — از صفر تا صد
• ﻣﻌﺎدﻻت دﯾﻔﺮاﻧﺴﯿﻞ ﺑﺎ ﻣﺸﺘﻘﺎت ﺟﺰﺋﯽ — از صفر تا صد
• معادله دیفرانسیل بسل — به زبان ساده

^^