قضیه آپولونیوس – به زبان ساده

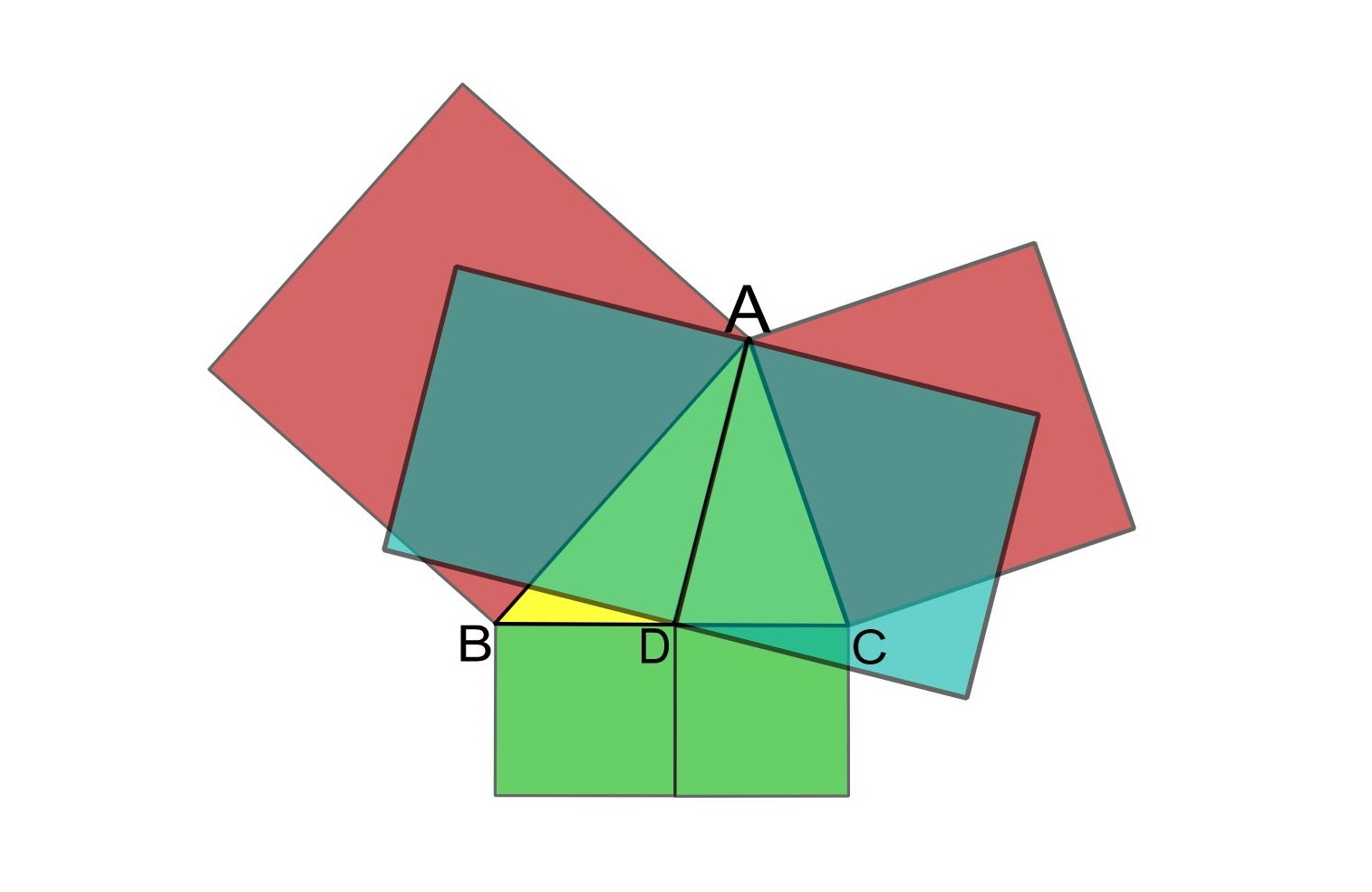
قضیه آپولونیوس یکی از قضایای هندسه مقدماتی است که طول میانه مثلث را به طول اضلاع آن مرتبط می‌کند. در حالی که در جهان این قضیه را به همین نام می‌شناسند، در شرق آسیا، این قضیه معمولاً به عنوان «قضیه پاپوس» (Pappus's Theorem) یا «قضیه نقطه میانی» (Midpoint Theorem) شناخته می‌شود. این قضیه را می‌توان با استفاده از قضیه فیثاغورس، قانون کسینوس‌ها و نیز بردارها اثبات كرد. قضیه آپولونیوس، به افتخار ریاضیدان یونانی، «آپولونیوس» (Apollonius)، نامگذاری شده است.

قضیه آپولونیوس

مثلث $$ABC$$ را در نظر بگیرید که در آن، $$M$$ نقطه میانی یا وسط $$\overline{BC}$$ است. قضیه آپولونیوس رابطه زیر را بیان می‌کند:

$$\large \overline { A B } ^ 2 + \overline { A C } ^ 2 = 2 \left\{ \overline { A M } ^ 2 + \left ( \frac { \overline { B C } }{ 2 } \right ) ^ 2 \right \} .$$

اثبات قضیه آپولونیوس با قضیه فیثاغورس

با استفاده از قضیه فیثاغورس، صحت قضیه آپولونیوس را برای مثلث $$ABC$$ که در آن، $$M$$ نقطه وسط $$\overline{BC}$$ است، اثبات می‌کنیم.

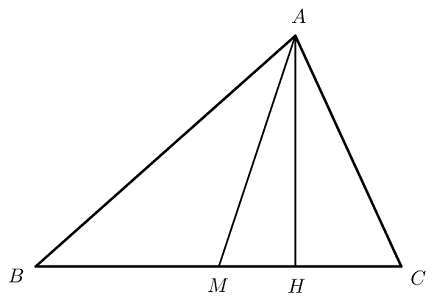
فرض کنید $$H$$ نقطه برخورد خط عمود بر $$\overline{BC}$$ باشد که از نقطه $$A$$ رسم شده است. بنابراین، خواهیم داشت:

$$\large \begin {aligned} \overline {B M } = \overline { C M } & = \frac { \overline { B C } } { 2 } \\\\ \overline { B H } + \overline { C H } & = \overline { B C } . \end {aligned}$$

با استفاده از قضیه فیثاغورس، می‌توان نوشت:

$$\large \begin {aligned} \overline { A B } ^ 2 & = \overline { A H } ^ 2 + \overline { B H } ^ 2 \\ \overline { A C } ^ 2 & = \overline { A H } ^ 2 + \overline { C H } ^ 2 \\ \overline { A M } ^ 2 & = \overline { A H } ^ 2 + \overline { M H } ^ 2 . \end {aligned}$$

با توجه به روابط بالا، خواهیم داشت:

$$\large \begin {aligned} \overline { A B } ^ 2 + \overline { A C } ^ 2 & = 2 \overline { A H } ^ 2 + \overline { B H } ^ 2 + \overline { C H } ^ 2 \\ & = 2 \overline { A H } ^ 2 + 2 \overline { M H } ^ 2 + \overline { B H } ^ 2 -\overline { M H } ^ 2 + \overline { C H } ^ 2 - \overline { M H } ^ 2 \\ & = 2 \overline { A M } ^ 2 + \left ( \overline { B H } + \overline { M H } \right ) \left ( \overline { B H } -\overline { M H } \right ) + \left ( \overline { C H } + \overline { M H } \right ) \left ( \overline { C H } - \overline { M H } \right ) \\ & = 2 \overline { A M } ^ 2 + \left ( \overline { B H } + \overline { M H } \right ) \cdot \overline { B M } + \overline { C M } \cdot \left ( \overline { C H } - \overline { M H } \right ) \\ & = 2 \overline { A M } ^ 2 + \frac { \overline { B C } ^ 2 } { 2 } \\ & = 2 \left \{ \overline { A M } ^ 2 + \left ( \frac { \overline { B C } }{ 2 } \right ) ^ 2 \right \} . \ _ \square \end {aligned}$$

اثبات قضیه آپولونیوس با قانون کسینوس‌ها

با استفاده از قانون کسینوس‌ها، صحت قضیه آپولونیوس را برای مثلث $$ABC$$ که در آن، $$M$$ نقطه میانی $$\overline{BC}$$ است، اثبات می‌کنیم.

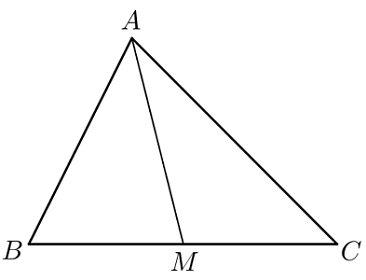
با استفاده از قانون کسینوس‌ها، می‌توان نوشت:

$$\large \begin {aligned} \overline { A B } ^ 2 & = \overline { B M } ^ 2 + \overline { A M } ^ 2 - 2 \overline { A M } \cdot \overline { B M } \cos \angle A M B \\\\ \overline { A C } ^ 2 & = \overline { C M } ^ 2 + \overline { A M } ^ 2 - 2 \overline { A M } \cdot \overline { C M } \cos \angle A M C \\ & = \overline { B M } ^ 2 + \overline { A M } ^ 2 + 2 \overline { A M } \cdot \overline { B M } \cos \angle A M B . \qquad ( \text {since } \angle A M B + \angle A M C = \pi ) \end {aligned}$$

با جمع این دو رابطه، خواهیم داشت:

$$\large \begin {aligned} \overline { A B } ^ 2 + \overline { A C } ^ 2 & = 2 \overline { A M } ^ 2 + 2 \overline { B M } ^ 2 \\ & = 2 \left \{ \overline { A M } ^ 2 + \left ( \frac { \overline { B C } } { 2 } \right ) ^ 2 \right \} . \ _ \square \end {aligned}$$

اثبات قضیه آپولونیوس با استفاده از بردارها

با استفاده از عملیات مقدماتی بردارها، صحت قضیه آپولونیوس را برای مثلث $$ABC$$ که در آن، $$M$$ نقطه میانی $$\overline{BC}$$ است، اثبات می‌کنیم.

فرض کنید $$A$$ مرکز یک دستگاه مختصات دکارتی باشد. با تعریف $$\overrightarrow { A B } = \overrightarrow { b }$$ و $$\overrightarrow { A C } = \overrightarrow { c }$$، تساوی‌های $$\overrightarrow { B C } = \overrightarrow { c } -\overrightarrow { b }$$ و $$\overrightarrow { A M } = \frac { \overrightarrow { b } + \overrightarrow { c } } { 2 }$$ را خواهیم داشت.

بنابراین، می‌توان نوشت:

$$\large \begin {aligned} \overline { A B } ^ 2 + \overline { A C } ^ 2 & = | \overrightarrow { b } | ^ 2 + | \overrightarrow { c } | ^ 2 \\ & = \dfrac { 1 } { 2 } \big ( 2 | \overrightarrow { b } | ^ 2 + 2 | \overrightarrow { c } | ^ 2 \big ) \\ & = \dfrac { 1 } { 2 } \big ( | \overrightarrow { b } | ^ 2 + | \overrightarrow { c } | ^ 2 + 2 \overrightarrow { b } \cdot \overrightarrow { c } + | \overrightarrow { b } | ^ 2 + | \overrightarrow { c } | ^ 2 - 2 \overrightarrow { b } \cdot \overrightarrow { c } \big ) \\ & = \dfrac { 1 } { 2 } \left \{ \big ( \overrightarrow {b } + \overrightarrow { c } ) ^ 2 + ( \overrightarrow { c } - \overrightarrow { b } \big ) ^ 2 \right \} \\ & = \dfrac { 1 } { 2 } \left ( 4 \overline { A M } ^ 2 + \overline { B C } ^ 2 \right ) \\ & = 2 \left \{ \overline { A M } ^ 2 + \left ( \dfrac { \overline { B C } } { 2 } \right ) ^ 2 \right \} . \ _ \square \end {aligned}$$

قضیه آپولونیوس و قضایای دیگر

قضیه آپولونیوس حالت خاصی از قضیه استوارت و همچنین، تعمیمی از قضیه فیثاغورس است.

فیلم آموزش هندسه ۳ – پایه دوازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

با جایگذاری $$\overline { B P } = \overline { C P }$$ در قضیه استوارت، یعنی $$\overline { C P } \cdot \overline { A B } ^ 2 + \overline { B P } \cdot \overline { A C } ^ 2 = \left ( \overline { B P } + \overline { C P } \right ) \left ( \overline { A P } ^ 2 + \overline { B P } \cdot \overline { C P } \right )$$، خواهیم داشت:

$$\large \overline { A B } ^ 2 + \overline { A C } ^ 2 = 2 \left ( \overline { A P } ^ 2 + \overline { B P } ^ 2 \right ) .$$

همچنین، مقادیر $$\angle BAC=\frac{\pi}{2}$$ و $$\overline{AM}=\frac{\overline{BC}}{2}$$ را در قضیه استوارت قرار می‌دهیم. در نتیجه، می‌توانیم بنویسیم:

$$\large \begin {aligned} \overline { A B } ^ 2 + \overline { A C } ^ 2 & = 2 \left \{ \left ( \frac { \overline { B C } } { 2 } \right ) ^ 2 + \left ( \frac { \overline { B C } } { 2 } \right ) ^ 2 \right \} \\ & = \overline { B C } ^ 2 . \ _ \square \end {aligned}$$

همچنین می‌توانیم «قضیه کارنو» (Carnot's Theorem) را برای نقطه $$P$$ به دست آوریم:

$$\large P A ^ 2 + P B ^ 2 + P C ^ 2 = G A ^ 2 + G B ^ 2 + G C ^ 2 + 3 P G ^ 2$$

مثال اول قضیه آپولونیوس

مثلث $$ABC$$ دارای اضلاع $$\overline{AB}=2\sqrt{3}$$ و $$\overline{BC}=2$$ است. $$D$$ نقطه میانی $$\overline{BC}$$ است و اندازه $$\overline{AD}=\sqrt{7}$$ را داریم.

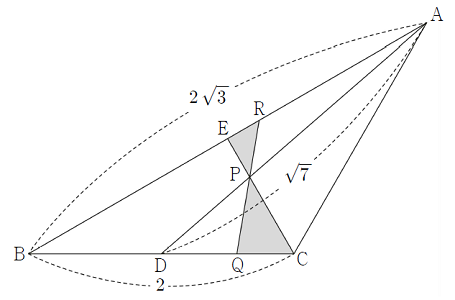
فرض کنید $$E$$ نقطه تقاطع بین $$\overline{AB}$$ و نیمساز $$\angle ACB$$ باشد. $$\overline{CE}$$ خط $$\overline{AD}$$ را در نقطه $$P$$ قطع می‌کند، و نیمساز $$\angle APE$$ در نقطه $$R$$ با $$\overline{AB}$$ برخورد دارد. امتداد $$\overline{PR}$$، خط $$\overline{BC}$$ را در $$Q$$ قطع خواهد کرد.

مساحت $$\triangle PQC$$ به اندازه $$a+b\sqrt{7}$$ برابر بزرگ‌تر از مساحت $$\triangle PRE$$ است که در آن، $$a$$ و $$b$$ اعدادی گویا هستند. مقدار $$a b$$ را به دست آورید.

حل: مقدار $$\overline{AC}=2$$ را داریم و بنابراین، $$\triangle ABC$$ یک مثلث حاده است که در آن، رابطه $$\overline{BE}=\overline{AE}=\sqrt{3}$$ و $$\overline{CE}=1$$ برقرار است.

از آنجا که $$\overline{CE}$$ و $$\overline{AD}$$ هر دو میانه $$\triangle ABC$$ هستند، مقادیر $$\overline{PE}=\dfrac{1}{3}$$، $$\overline{PC}=\dfrac{2}{3}$$، $$\overline{PA}=\dfrac{2\sqrt{7}}{3}$$ و $$\overline{PD}=\dfrac{\sqrt{7}}{3}$$ را خواهیم داشت. $$P$$ مرکزوار (محل تلاقی سه میانه) $$\triangle ABC$$ است.

$$\overline{QR}$$ زاویه‌های $$\angle APE$$ و $$\angle CPD$$ را به دو قسمت مساوی تقسیم می‌کند، بنابراین، می‌دانیم روابط $$\overline{RA}:\overline{RE}=\overline{PA}:\overline{PE}=2\sqrt{7}:1$$ و $$\overline{QD}:\overline{QC}=\overline{PD}:\overline{PC}=\sqrt{7}:2$$ برقرارند. در نتیجه، روابط $$\triangle PRE=\dfrac{1}{2\sqrt{7}+1}\triangle APE$$ و $$\triangle PQC=\dfrac{2}{2+\sqrt{7}}\triangle CPD$$ را خواهیم داشت.

با توجه به اینکه $$P$$ مرکزوار است، $$\triangle APE=\triangle CPD$$ و داریم:

$$\large \begin {aligned} a + b \sqrt { 7 } & = \dfrac { \dfrac { 2 } { 2 + \sqrt { 7 } } } { \dfrac { 1 } { 2 \sqrt { 7 } + 1 } } \\ \\ & = \dfrac { 2 ( 2 \sqrt { 7 } + 1 ) } { \sqrt { 7 } + 2 } \\ \\ & = \dfrac { 2 ( 2 \sqrt { 7 } + 1 ) ( \sqrt { 7 } - 2 ) } { 3 } \\ \\ & = \dfrac { 2 ( 1 2 - 3 \sqrt { 7 } ) } { 3 } \\ \\ & = 8 - 2 \sqrt { 7 } . \end {aligned}$$

در نتیجه، جواب مسئله به صورت زیر است:

$$\large \therefore \, ab=8\cdot(-2)=\boxed{-16}$$

مثال دوم قضیه آپولونیوس

مثلث $$ABC$$ با مرکزوار $$G$$ دارای اضلاع $$AB=15$$، $$BC=18$$ و $$AC=25$$ است. همچنین، $$D$$ نقطه میانی $$BC$$ است. طول $$GD$$ را می‌توان به صورت $$\frac{ a \sqrt{d} } { b}$$ نوشت که در آن، $$a$$ و $$b$$ اعداد صحیح مثبتی هستند که نسبت به هم اول‌اند و $$d$$ یک عدد صحیح مثبت است که جذر صحیح ندارد. مقدار $$a + b + d + 1$$ را محاسبه کنید.

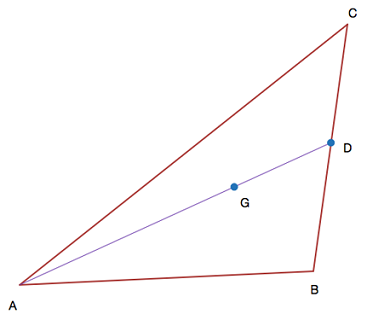
حل:‌ اندازه $$A D$$ را با استفاده از فرمولی که از قضیه استوارت برای میانه‌ها به دست آمده، می‌نویسیم:

$$\large \begin {align*} A D & = \dfrac { \sqrt { 2 ( A B ^ 2 + A C ^ 2 ) - B C^ 2 } } { 2 } \\ A D & = \dfrac { \sqrt { 2 ( 1 5 ^ 2 + 2 5 ^ 2 ) -1 8 ^ 2 } } { 2 } \\ A D & = \dfrac { \sqrt { 1 3 7 6 } } { 2 } = 2 \sqrt { 8 6 } \end {align*}$$

اکنون، از آنجا که میانه‌ها خودشان را در مرکزوار با نسبت ۲:۱ از رأس به نقطه میانی قطع می‌کنند، خواهیم داشت:

$$\large G D = \dfrac { A D } { 3 } = \dfrac { 2 \sqrt { 8 6 } }{ 3 }$$

بنابراین، $$a=2$$، $$b = 3$$ و $$d = 86$$ است. در نتیجه، مقدار $$a +b +d+1= 92$$ به دست خواهد آمد.