ضریب دید در تشعشع – از صفر تا صد

انتقال حرارت تشعشعی بین سطوح مختلف به عوامل بسیاری وابسته است. جهت‌گیری سطوح نسبت به هم و همچنین ویژگی‌های تشعشی و دمای آنها از مهمترین عواملی هستند که باید نام برد. شخصی را که در جلوی آتش نشسته در نظر بگیرید. از یک طرف سعی می‌کند در نزدیک‌ترین فاصله ممکن از آتش بنشیند و از طرف دیگر، کف دست‌هایش را طوری در مسیر گرما قرار می‌دهد تا بیشترین گرمای ممکن را از آتش دریافت کند. در این مقاله، ضریب دید را در تشعشع تعریف می‌کنیم و نقش آن را در این شیوه از انتقال حرارت بررسی خواهیم کرد.

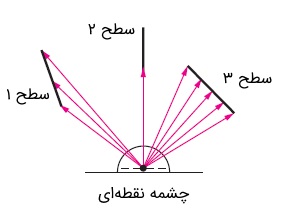
برای اینکه بتوانیم اثرات جهت‌گیری دو سطح نسبت به هم را در تشعشع بررسی کنیم، پارامتر جدیدی به نام ضریب دید (View Factor) تعریف می‌شود. ضریب دید یک کمیت هندسی بوده و مستقل از ویژگی‌ها و دمای سطح است. ضریب شکل (Shape Factor) و ضریب زاویه (Angle Factor)، نام‌های دیگریست که به این کمیت گفته می‌شود. ضریب دید از سطح $$\large i$$ به سطح $$\large j$$ را با نماد $$\large F_ {i\rightarrow j}$$ یا $$\large F_ {ij}$$ نشان می‌دهیم. ضریب دید $$\large F_ {ij}$$ به عنوان کسری از تشعشع خارج شونده از سطح $$\large i$$ تعریف می‌شود که مستقیماً به سطح $$\large j$$ برخورد می‌کند.

در واقع نماد $$\large F_ {i\rightarrow j}$$ کاملاً گویای تعریف ضریب دید است و بخشی از تشعشع را نشان می‌دهد که از سطح $$\large i$$ به سطح $$\large j$$‌ منتقل می‌شود. ولی بهتر است در هنگام نوشتن معادلات پیچیده، برای ساده‌تر شدن از نماد $$\large F_ {ij}$$ استفاده کنیم. این نکته را به خاطر داشته باشید که وقتی تشعشع به سطحی برخورد می‌کند، نیاز نیست تا لزوماً توسط آن سطح، جذب شود. همچنین اگر در مسیر رسیدن تشعشع از سطح $$\large i$$ به سطح $$\large j$$، سطح سومی نقش واسطه را داشته باشد، در محاسبه ضریب دید وارد نخواهد شد.

محاسبه ضریب دید

برای اینکه بتوانیم ضریب دید را به صورت ریاضی بیان کنیم، دو سطح دیفرانسیلی مختلف $$\large dA_1$$ و $$\large dA_2$$ را در نظر بگیرید که روی سطوح $$\large A_1$$ و $$\large A_2$$ و با جهت‌گیری دلخواه قرار دارند. فاصله بین $$\large dA_1$$ و $$\large dA_2$$ برابر $$\large r$$ و زاویه بین عمودهای این دو سطح و خطی که $$\large dA_1$$ و $$\large dA_2$$ را به یکدیگر متصل می‌کند، به ترتیب با $$\large \theta_1$$ و $$\large \theta_2$$ نشان داده شده است.

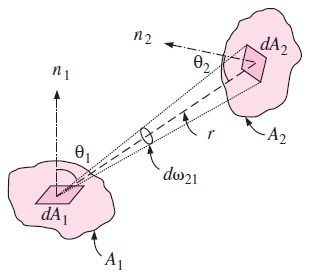
سطح شماره یک، امواج تشعشعی را با شدت یکسان $$\large I_1$$، به صورت واگرا و در همه جهت‌ها منتشر می‌کند. زاویه دید سطح $$\large dA_2$$ از سطح $$\large dA_1$$ نیز برابر $$\large d\omega _{21}$$ است. تشعشع با نرخ $$\large I_1 \cos \theta _1\text {d}A_1$$ و در زاویه $$\large \theta_1$$ سطح $$\large \text {d} A_1$$ را ترک می‌کند. به این ترتیب، قسمتی از تشعشع که به سطح $$\large \text {d} A_2$$ برخورد می‌کند به طریق زیر محاسبه می‌شود.

$$\large \text {d} \omega _{21} \:=\: \text {d}A_2 \cos \theta_2 /r^2 \\~\\ \large \Rightarrow ~~~ \dot{Q} _{dA_1 \rightarrow dA_2} \:=\: I_1 \cos \theta_1 \text {d} A_1 \text {d} \omega _{21} \:=\: I_1 \cos \theta_1 \text {d} A_1 \frac {\text {d} A_2 \cos \theta_2} {r^2}$$

نرخ کل تشعشعی که سطح $$\large \text {d} A_1$$ را در تمام جهت‌ها ترک می‌کند برابر با حاصل‌ضرب شار تشعشع خروجی کل (Radiosity) در اندازه سطح است.

$$\large J_1\:=\: \pi I_1 \\~\\ \large \Rightarrow ~~~ \dot{Q} _{dA_1} \:=\: J_1 \text {d} A_1 \:=\: \pi I_1 \text {d} A_1$$

سپس ضریب دید دیفرانسیلی $$\large \text {d} F_ {dA_1 \rightarrow dA_2}$$ را تعریف می‌کنیم که برابر با کسری از تشعشع خارج شونده از $$\large \text {d} A_1$$ است که به $$\large \text {d} A_2$$ برخورد می‌کند.

$$\large \text {d} F_ {dA_1 \rightarrow dA_2} \:=\: \frac {\dot {Q} _{dA_1 \rightarrow dA_2}} {\dot {Q} _{dA_1}} \:=\: \frac {\cos \theta_1 \cos \theta_2} {\pi r^2} \text {d} A_2$$

حالا ضریب دید از سطح دیفرانسیلی $$\large \text {d} A_1$$ به سطح $$\large A_2$$ را تعیین می‌کنیم. کسری از تشعشع خارج شونده از $$\large \text {d} A_1$$ که به سطح $$\large A_2$$ برخورد می‌کند با مجموع کسرهای تشعشعی که به سطوح $$\large \text {d} A_2$$ برخورد کرده‌اند برابر است. بدین منظور، برای تعیین ضریب دید $$\large F_ {dA_1 \rightarrow dA_2}$$، روی سطح $$\large A_2$$ از $$\large \text {d} F_ {dA_1 \rightarrow dA_2}$$ انتگرال می‌گیریم.

$$\large F_ {dA_1 \rightarrow dA_2} \:=\: \int_{A_2}^{} \frac {\cos \theta_1 \cos t\theta_2} {\pi r^2} \text {d} A_2$$

نرخ کل تشعشعی که سطح $$\large A_1$$ را در همه جهت‌ها ترک می‌کند، به صورت زیر است.

$$\large \dot{Q} _{A_1} \:=\: J_1 A_1 \:=\: \pi I_1 A_1$$

کسری از تشعشع که به سطح دیفرانسیلی $$\large \text {d} A_2$$ برخورد می‌کند را با در نظر گرفتن تشعشع خارج شونده از $$\large \text {d} A_1$$ و برخورد کننده به $$\large \text {d} A_2$$ و سپس انتگرال‌گیری از آن روی سطح $$\large A_1$$ محاسبه می‌کنیم.

$$\large \dot{Q} _{A_1 \rightarrow dA_2} \:=\: \int_ {A_1}^{} \dot {Q} _{dA_1 \rightarrow dA_2} \:=\: \int_ {A_1}^{} \frac {I_1 \cos \theta_1 \cos \theta_2 dA_2} {r^2} dA_1$$

اکنون اگر از رابطه به دست‌ آمده در بالا روی سطح $$\large A_2$$ انتگرال بگیریم، کل تشعشعی که به سطح $$\large A_2$$ برخورد می‌کند، به دست خواهد آمد.

$$\large \dot {Q} _{A_1 \rightarrow A_2} \:=\: \int_{A_2}^{} \dot {Q} _{A_1 \rightarrow dA_2} \:=\: \int_{A_2}^{} \int_{A_1}^{} \frac {I_1 \cos \theta_1 \cos \theta_2} {r^2} dA_1 dA_2$$

با تقسیم رابطه بالا به نرخ کل تشعشع خارج شونده از سطح $$\large A_1$$، ضریب دید $$\large F_ {A_1 \rightarrow A_2}$$ (یا به اختصار $$\large F_ {12}$$) به دست می‌آید که برابر با کسری از تشعشع خارج شونده از سطح $$\large A_1$$ است که به سطح $$\large A_2$$ برخورد می‌کند.

$$\large F_{12} \:=\: F_ {A_1 \rightarrow A_2} \:=\: \frac {\dot {Q}_ {A_1 \rightarrow A_2}} {\dot {Q} _{A_1}} \:=\: \frac {1} {A_1} \int_{A_2}^{} \int_{A_1}^{} \frac {\cos \theta_1 \cos \theta_2} {\pi r^2} dA_1 dA_2$$

همچنین $$\large F_ {A_2 \rightarrow A_1}$$ نیز با جابجا کردن اندیس‌ها و به راحتی نوشته می‌شود.

$$\large F_{21} \:=\: F_ {A_2 \rightarrow A_1} \:=\: \frac {\dot {Q}_ {A_2 \rightarrow A_1}} {\dot {Q} _{A_2}} \:=\: \frac {1} {A_2} \int_{A_2}^{} \int_{A_1}^{} \frac {\cos \theta_1 \cos \theta_2} {\pi r^2} dA_1 dA_2$$

توجه کنید که $$\large I_1$$ ثابت بوده ولی $$\large r$$، $$\large \theta _1$$ و $$\large \theta _2$$ متغیر هستند. این روابط تأیید می‌کند که ضریب دید بین دو سطح مختلف به جهت‌گیری آنها نسبت به هم و فاصله‌شان از یکدیگر بستگی دارد.

با ادغام دو رابطه اخیر، نتیجه زیر حاصل می‌شود.

$$\large A_1 F_{12} \:=\: A_2 F_ {21}$$

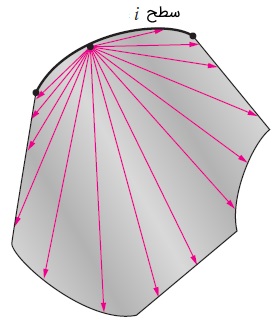
رابطه بالا به رابطه تقابل (Reciprocity Relation) برای ضریب دید معروف است. با کمک این رابطه، اگر ضریب دید سطح اول مشخص باشد، می‌توانیم به راحتی ضریب دید سطح دوم را محاسبه کنیم. روابطی که تا اینجا برای ضریب دید معرفی شد را می‌توان برای هر دو سطح $$\large i$$ و $$\large j$$ که در آنها شدت تشعشع ثابت است، به کار برد. توجه کنید که در غیاب میدان الکترومغناطیسی قوی، امواج تشعشع در مسیر مستقیم حرکت می‌کنند. ضریب دید از هر سطحی نسبت به خودش صفر است؛ مگر این‌که آن سطح خودش را «ببیند». در نتیجه، ضریب دید در سطوح صاف و محدب برابر صفر ($$\large F_{i \rightarrow i} =0$$) بوده ولی در سطوح مقعر مخالف صفر ($$\large F_{i \rightarrow i} \neq0$$) است. شکل زیر این موضوع را به خوبی نشان می‌دهد.

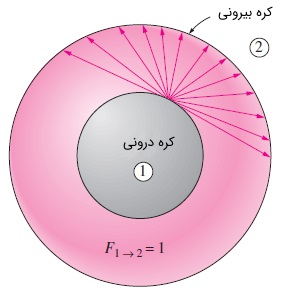
مقدار ضریب دید همواره عددی بین صفر و یک است. در حالت حدی $$\large F_{i \rightarrow j} =0$$، دو سطح هیچ دید مستقیمی به هم ندارند و تشعشع خروجی از سطح $$\large i$$ نمی‌تواند مستقیماً به سطح $$\large j$$ برخورد کند. همچنین در سوی دیگر و در حالتی که $$\large F_{i \rightarrow j} =1$$ برقرار باشد، سطح $$\large j$$ به طور کامل، سطح $$\large i$$ را احاطه کرده و تمام تشعشع خروجی از سطح $$\large i$$ به سطح $$\large j$$ می‌رسد. به عنوان مثالی از این حالت، می‌توانید دو کره هم‌مرکز را در نظر بگیرید که یکی در داخل دیگری قرار داشته باشد. در این حالت، تمام تشعشع خروجی از سطح کره کوچکتر، به سطح داخلی کره بزرگتر برخورد می‌کند و ضریب دید برابر یک خواهد بود. به شکل زیر توجه کنید.

ضریب دید نقش زیادی در تحلیل انتقال گرما از طریق تشعشع دارد. زیرا اجازه می‌دهد تا کسر تشعشع خروجی از یک سطح را که به سطحی دیگر برخورد می‌کند، برحسب جهت‌گیری آن دو سطح نسبت به هم بیان کنیم. نکته مهم این‌جاست که تشعشع دریافتی سطح از چشمه، مستقیماً با زاویه‌ای که سطح از روی چشمه دیده می‌شود، متناسب است. این حالت تنها هنگامی رخ می‌دهد که امواج گسیل شده از چشمه در همه جهت‌ها و به صورت یکنواخت حرکت کنند و فضای بین سطح و چشمه، امواج را جذب یا پراکنده نکند.

ضریب دید در هندسه‌های متداول

ضریب دید در بسیاری از هندسه‌های متداول به روش‌های مختلف تحلیلی، گرافیکی و غیره مشخص شده است. در این قسمت، ضریب دید مربوط به برخی از هندسه‌ها ارائه شده است.

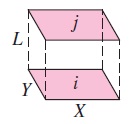
دو مستطیل را مطابق شکل زیر در نظر بگیرید که در مقابل یکدیگر قرار گرفته‌اند. روابط مربوط به این هندسه به صورت زیر است.

$$\large \overline{X} \:=\: X/L \\~\\ \large \overline{Y} \:=\: Y/L \\~\\ \large F_{i \rightarrow j} \:=\: \frac {2} {\pi \overline{X} \overline{Y}} \left\{ \ln \left[ \frac {(1\:+\: \overline{X} ^2) (1\:+\: \overline{Y} ^2)} {1\:+\: \overline{X} ^2 \:+\: \overline{Y} ^2} \right] ^ {1/2} \\~\\ \large +\: \overline{X} (1\:+\: \overline{Y} ^2) ^{1/2} \tan ^{-1} \frac {\overline{X}} {(1\:+\: \overline{Y} ^2) ^{1/2}} \\~\\ \large +\: \overline{Y} (1\:+\: \overline{X} ^2) ^{1/2} \tan ^{-1} \frac {\overline{Y}} {(1\:+\: \overline{X} ^2) ^{1/2}} \\~\\ \large -\:\overline{X} \tan ^{-1} \overline{X} \:-\: \overline{Y} \tan ^{-1} \overline{Y} \right\}$$

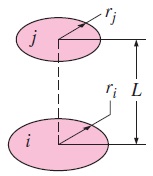
شکل زیر دو دایره هم‌مرکز را نشان می‌دهد که در مقابل هم قرار دارند و فاصله عمودی بین آنها برابر $$\large L$$ است. اگر شعاع این دو دایره $$\large r_i$$ و $$\large r_j$$ باشد، ضریب دید بین آنها به صورت زیر به دست می‌آید.

$$\large R_i \:=\: r_i /L \\~\\ \large R_j \:=\: r_j /L \\~\\ \large S\:=\: 1\:+\: \frac {1\:+\: R^2_j} {R_i^2} \\~\\ \large F_{i\rightarrow j} \:=\: \frac {1} {2} \left\{ S\:-\: \left[ S^2 \:-\: 4\left( \frac {r_j} {r_i} \right) ^2 \right] ^{1/2} \right\}$$

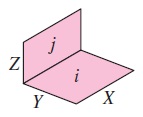
دو مستطیل زیر به هم عمودند و یکی از اضلاعشان نیز مشترک است. برای محاسبه ضریب دید بین این دو شکل به ترتیب زیر عمل می‌کنیم.

$$\large H\:=\: Z/X \\~\\ \large W\:=\: Y/X \\~\\ \large F_{i\rightarrow j} \:=\: \frac {1} {\pi W} \left( W\tan ^{-1} \frac {1} {W} \:+\: H\tan ^{-1} \frac {1} {H} \\~\\ \large -\: (H^2 \:+\: W^2) ^{1/2} \tan ^{-1} \frac {1} {(H^2 \:+\: W^2) ^{1/2}} \\~\\ \large +\: \frac {1} {4} \ln \left\{ \frac {(1\:+\: W^2) (1\:+\: H^2)} {1\:+\: W^2 \:+\: H^2} \\~\\ \large \times \: \left[ \frac {W^2 (1\:+\: W^2 \:+\: H^2)} {(1\:+\: W^2) (W^2 \:+\: H^2)} \right] ^{W^2} \\~\\ \large \times \: \left[ \frac {H^2 (1\:+\: H^2 \:+\: W^2)} {(1\:+\: H^2) (H^2 \:+\: W^2)} \right] ^{H^2} \right\} \right)$$

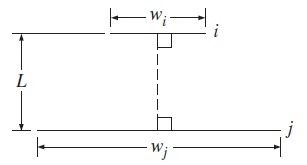
شکل‌هایی که در ادامه بررسی خواهیم کرد، دو بُعدی بوده و طول بُعد سومشان، بی‌نهایت فرض شده است. در شکل زیر، ضریب دید را بین دو صفحه موازی محاسبه می‌کنیم که فاصله عمودی بین آنها $$\large L$$ است.

$$\large W_i \:=\: w_i /L \\~\\ \large W_j \:=\: w_j /L \\~\\ \large F_ {i \rightarrow j} \:=\: \frac {\left[ (W_i \:+\: W_j) ^2 \:+\: 4 \right] ^{1/2} \:-\: \left[ \left( W_j \:-\: W_i \right) ^2 \:+\: 4 \right] ^{1/2}} {2W_i}$$

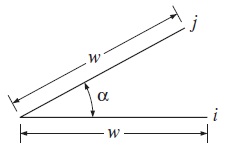
در شکل زیر دو صفحه متقاطع با عرض یکسان داریم که یک لبه مشترک دارند. ضریب دید برای این دو صفحه که زاویه بینشان برابر $$\large \alpha$$ است به صورت زیر نوشته می‌شود.

$$\large F_ {i \rightarrow j} \:=\: 1\:-\: \sin \frac {1} {2} \alpha$$

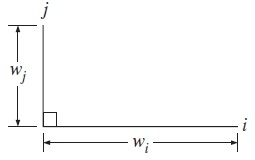
بالاخره در آخرین شکلی که در این قسمت بررسی می‌کنیم، دو صفحه با عرض‌های $$\large w_i$$ و $$\large w_j$$ به هم عمودند و یک لبه مشترک دارند.

$$\large F_ {i \rightarrow j} \:=\: \frac {1} {2} \left\{ a\:+\: \frac {w_j} {w_i} \:-\: \left[ 1\:+\: \left( \frac {w_j} {w_i} \right) ^2 \right] ^{1/2} \right\}$$

رابطه‌های مهم در ضریب دید

تحلیل تشعشع در سیستمی که از $$\large N$$ سطح تشکیل شده، مستلزم آن است که تعداد $$\large N^2$$ ضریب دید محاسبه شود. این قسمت از کار احتمالاً وقت‌گیرترین قسمت در تحلیل تشعشع یک سیستم خواهد بود. ولی نه عملی و نه ضروری است که وقتمان را صرف محاسبه تک‌تک ضرایب دید کنیم. باید راهی وجود داشته باشد تا پس از به دست آوردن چند ضریب دید مابقی آنها با روابط ساده‌تر مشخص شوند. در این بخش، برخی از این روابط را معرفی می‌کنیم.

اصل تقابل

دو ضریب دید $$\large F_ {i \rightarrow j}$$ و $$\large F_ {j \rightarrow i}$$ با هم معادل نیستند. فقط در صورتی که $$\large A_i = A_j$$ برقرار باشد، می‌توان رابطه $$\large F_ {i \rightarrow j} = F_ {j \rightarrow i}$$ را نوشت. در غیر این صورت ($$\large A_i \neq A_j$$)، رابطه به شکل $$\large F_ {i \rightarrow j} \neq F_ {j \rightarrow i}$$ خواهد بود. همان‌طور که قبلاً گفتیم، رابطه زیر که به اصل تقابل (Reciprocity Rule) معروف است را می‌توان بین این دو ضریب دید نوشت. در واقع با کمک این رابطه، می‌توانیم از بین $$\large F_ {i \rightarrow j}$$ و $$\large F_ {j \rightarrow i}$$ هرکدام که ساده‌تر بود را ابتدا محاسبه کرده و سپس با کمک رابطه تقابل، ضریب دید متقابل آن را به دست آوریم.

اصل حاصل‌ جمع

تحلیل تشعشع یک سطح در حالت عادی نیازمند آن است که امواج ورودی و خروجی در همه جهت‌ها در نظر گرفته شوند. بنابراین در بیشتر مسائل مربوط به تشعشع، با حجم‌های بسته سر و کار خواهیم داشت. هنگام تحلیل یک مسئله تشعشعی، فضای بسته‌ای رسم می‌کنیم تا تمام سطوحی که در تشعشع درگیر هستند، درون آن قرار بگیرند. در چنین روشی، حتی دریچه‌های باز هم به عنوان سطوح فرضی در نظر گرفته می‌شوند که رفتار تشعشعی آنها با دریچه‌های باز معادل باشد.

اصل پایستگی انرژی نیازمند این است که تمام تشعشع خارج شونده از هر سطح $$\large i$$ مربوط به این محفظه به سطوح آن برخورد کند. بنابراین، حاصل‌جمع ضرایب دید مربوط به سطح $$\large i$$ از یک محفظه، نسبت به تمام سطوح آن محفظه، که شامل سطح $$\large i$$ هم می‌شود، باید برابر یک باشد. این رابطه را که به عنوان اصل حاصل‌جمع (Summation Rule)‌ نامیده می‌شود، به صورت زیر تعریف می‌کنیم.

$$\large \sum_{j=1}^N F_ {i \rightarrow j} \:=\:1$$

در رابطه بالا، $$\large N$$ تعداد سطوح داخلی محفظه را نشان می‌دهد. به عنوان مثال، اگر رابطه حاصل‌جمع را برای سطح شماره ۱ در محفظه‌ای با ۳ سطح بنویسیم، به صورت زیر خواهد بود.

$$\large \sum_{j=1}^3 F_ {1 \rightarrow j} \:=\: F_ {1 \rightarrow 1} \:+\: F_ {1 \rightarrow 2} \:+\: F_ {1 \rightarrow 3} \:=\:1$$

رابطه حاصل‌جمع را می‌توانیم به هر سطحی در محفظه اعمال کرده و $$\large i$$ را هر مقداری در بازه $$\large 1$$ تا $$\large N$$ قرار دهیم. در نتیجه، اعمال رابطه حاصل‌جمع برای هریک از $$\large N$$ سطح داخل یک محفظه، در مجموع، $$\large N$$ رابطه برای تعیین ضرایب دید ایجاد می‌کند. همچنین، تعداد رابطه‌های متقابلی که به این عدد اضافه می‌شود برابر با $$\large \frac {1} {2} N(N -1)$$ است. در این صورت، تعداد کل ضرایب دید لازم که باید در یک محفظه $$\large N$$ سطحی به صورت مستقیم محاسبه شود، به صورت زیر است.

$$\large N^2 \:-\: \left[ N \:+\: \frac {1} {2} N (N \:-\: 1) \right] \:=\: \frac {1} {2} N (N \:-\: 1)$$

به عنوان مثال، در محفظه‌ای که از شش سطح تشکیل شده، باید $$\large \frac {1} {2} \times 6 (6 -1) =15$$ از $$\large 6^2 =36$$ ضریب دید را مستقیماً محاسبه کنیم. بیست و یک ضریب دید باقی‌مانده را می‌توان با کمک رابطه تقابل یا رابطه حاصل‌جمع به دست آورد.

مثال ۱: محاسبه ضریب دید در دو کره هم‌مرکز

سؤال: ضریب دید مربوط به محفظه تشکیل شده از دو کره هم‌مرکز شکل زیر را به دست آورید.

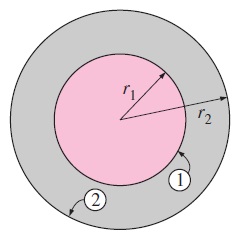
پاسخ: سطح بیرونی کره کوچکتر را سطح شماره ۱ و سطح داخلی کره بزرگتر را سطح شماره ۲ می‌نامیم. در نتیجه، در این محفظه $$\large N=2$$ است و این محفظه شامل $$\large N^2=4$$ ضریب دید است که شامل $$\large F_{11}$$، $$\large F_{12}$$، $$\large F_{21}$$ و $$\large F_{22}$$ می‌شود. در این محفظه دو سطحی فقط کافیست تا به تعدادی که در رابطه زیر به دست می‌آید، ضریب دید را مستقیماً محاسبه کنیم.

$$\large \frac {1} {2} N(N\:-\:1) \:=\: \frac {1} {2} \times 2(2\:-\:1) \:=\: 1$$

سه ضریب دید باقیمانده را می‌توان به راحتی و با اعمال رابطه‌های تقابل و حاصل‌جمع به دست آورد. ولی با کمی دقت متوجه می‌شویم که دو تا از این ضرایب دید را می‌توان به صورت مستقیم و با کمترین محاسبات ممکن محاسبه کرد. هیچ یک از امواج تشعشعی خارج شونده از سطح شماره، به همان سطح برخورد نمی‌کند. پس اولین ضریب دید را به صورت $$\large F_{11} \:=\: 0$$ یافتیم. دومین ضریب دید هم به صورت $$\large F_{12} \:=\: 1$$ است، زیرا تمام امواج خارج شونده از سطح ۱ به سطح ۲ برخورد می‌کنند. حالا می‌توانیم از رابطه حاصل‌جمع استفاده کنیم. اعمال این رابطه برای سطح شماره ۱، نتیجه $$\large F_{11} + F_{12} \:=\: 1$$ را در پی دارد؛ که با اعدادی که تا اینجا به دست آوردیم، سازگار است.

حالا از رابطه تقابل استفاده می‌کنیم تا ضریب دید $$\large F_{21}$$ تعیین شود.

$$\large A_1 F_{12} \:=\: A_2 F_ {21} \\~\\ \large \Rightarrow ~~~ F_{21} \:=\: \frac {A_1} {A_2}F_{12} \:=\: \frac {4\pi r^2_1} {4\pi r^2_2} \times 1 \:=\: (\frac {r_1} {r_2})^2$$

در نهایت نیز، چهارمین مجهول این مسئله که ضریب دید $$\large F_{22}$$ است، با کمک رابطه حاصل‌جمع به دست می‌آید.

$$\large F_{21} \:+\: F_ {22} \:=\: 1\\~\\ \large F_ {22} \:=\: 1\:-\: F_{21} \:=\: 1\:-\: \left( \frac {r_1} {r_2} \right) ^2$$

توجه کنید هنگامی که کره بیرونی نسبت به کره درونی خیلی بزرگتر باشد ($$\large r_2 \gg r_1$$) مقدار حدی ضریب دید $$\large F_{22}$$ به عدد یک میل می‌کند. این موضوع دور از انتظار نیست. زیرا در آن وضعیت، کسری از امواج تشعشعی خارج شونده از کره بیرونی که به کره درونی برخورد می‌کنند، قابل چشم‌پوشی خواهد بود.

اصل برهم‌نهی

حالت‌هایی پیش می‌آید که در آنها، ضریب دید هندسه مورد سؤال، در هیچ کتاب و جدول استانداردی از پیش تعیین نشده است. در چنین مواردی بهتر است هندسه مورد سؤال را به هندسه‌های کوچکتری تقسیم کنیم که ضریب دید هریک از آنها مشخص باشد. اصل برهم‌نهی (Superposition Rule) که در شاخه‌های مختلفی از علوم معتبر است، منجر به معرفی رابطه‌ای تحت عنوان رابطه برهم‌نهی می‌شود. براساس اصل برهم‌نهی، ضریب دید از سطح $$\large i$$ به سطح $$\large j$$ برابر با مجموع ضرایب دید از سطح $$\large i$$ به تک‌تک قسمت‌های سطح $$\large j$$ است. توجه کنید که برعکس این قانون درست نیست. یعنی ضریب دید از سطح $$\large j$$ به سطح $$\large i$$ را نمی‌توان با مجموع ضرایب دید از قسمت‌های سطح $$\large j$$ به سطح $$\large i$$ معادل دانست.

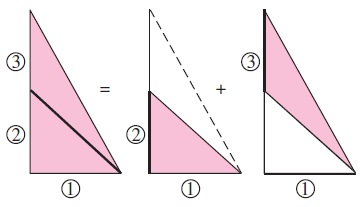
هندسه نشان داده شده در شکل بالا را در نظر بگیرید. طول بُعد سوم این شکل بینهایت بوده و عمود به صفحه است. تشعشع خارج شونده از سطح ۱ که به مجموع سطوح ۲ و ۳ برخورد می‌کند، با مجموع تشعشع برخورد کننده به سطح ۲ و سطح ۳ برابر است. در نتیجه، ضریب دید از سطح ۱ به سطح ترکیبی ۲ و ۳ به صورت زیر است.

$$\large F_ {1 \rightarrow (2,3)} \:=\: F_ {1 \rightarrow 2} \:+\: F_ {1 \rightarrow 3}$$

اکنون، اصل تقابل را به این رابطه اعمال می‌کنیم.

$$\large \left( A_2 \:+\: A_3 \right) F_ {(2,3) \rightarrow 1} \:=\: A_2 F_ {2 \rightarrow 1} \:+\: A_3 F_ {3 \rightarrow 1} \\~\\ \large \Rightarrow ~~~ F_ {(2,3) \rightarrow 1} \:=\: \frac {A_2 F_ {2 \rightarrow 1} \:+\: A_3 F_ {3 \rightarrow 1}} {A_2 \:+\: A_3}$$

برای سطوحی که به صورت مجموع بیش از دو سطح بیان می‌شوند نیز می‌توان از همین روش استفاده کرد.

مثال ۲: محاسبه کسر تشعشع خارج‌ شونده از دریچه

سؤال: کسر تشعشع خارج‌شونده از قاعده محفظه استوانه‌ای نشان داده شده در شکل زیر را محاسبه کنید. دریچه قرار گرفته در قاعده این محفظه با استوانه هم‌مرکز است. شعاع و ارتفاع این محفظه به ترتیب برابر با $$\large r_1 \:=\: 10\: cm$$ و $$\large L \:=\: 10\: cm$$ بوده و شعاع درونی و بیرونی دریچه نیز به ترتیب برابر با $$\large r_2 \:=\: 5\: cm$$ و $$\large r_3 \:=\: 8\: cm$$ است.

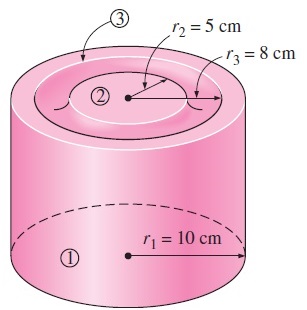
پاسخ: می‌خواهیم کسر تشعشع خارج‌شونده را از دریچه‌ای حلقوی که روی قاعده بالایی استوانه قرار دارد به دست آوریم. در واقع باید ضریب دید $$\large F_ {1\rightarrow \text {ring}}$$ را از قاعده محفظه به سطح حلقوی شکل پیدا کنیم. این مقدار به طور مستقیم یا از طریق جداول ضریب دید قابل محاسبه نیست. اما می‌توانیم بدین منظور از ضریب دید بین دو دایره موازی و هم‌مرکز کمک بگیریم.

سطح قاعده با شعاع $$\large r_1 \:=\: 10\: cm$$ را سطح شماره ۱ فرض می‌کنیم. دو دایره به شعاع‌های $$\large r_2 \:=\: 5\: cm$$ و $$\large r_3 \:=\: 8\: cm$$ را نیز به ترتیب سطوح شماره ۲ و ۳ در نظر می‌گیریم. با استفاده از اصل برهم‌نهی، ضریب دید از سطح ۱ به سطح ۳ به صورت زیر بیان می‌شود.

$$\large F_ {1\rightarrow 3} \:=\: F_ {1\rightarrow 2} \:+\: F_ {1\rightarrow \text {ring}}$$

می‌دانیم سطح ۳ برابر با مجموع سطوح ۲ و ناحیه حلقوی است. ضریب دید $$\large F_ {1\rightarrow 2}$$ و $$\large F_ {1\rightarrow 3}$$ را می‌توانیم با استفاده از جداول ضریب دید یا رابطه‌ای که برای ضریب دید دو دایره موازی و هم‌مرکز معرفی کردیم، محاسبه کنیم.

$$\large \frac {L} {r_1} \:=\: \frac {10\: cm} {10\: cm} \:=\:1 ~~~ ~~~ ~~~ \frac {r_2} {L} \:=\: \frac {5\: cm} {10\: cm} \:=\: 0.5 \\~\\ \large \Rightarrow ~~~ F_ {1 \rightarrow 2} \:=\: 0.11 \\~\\ \large \frac {L} {r_1} \:=\: \frac {10\: cm} {10\: cm} \:=\:1 ~~~ ~~~ ~~~ \frac {r_3} {L} \:=\: \frac {8\: cm} {10\: cm} \:=\: 0.8 \\~\\ \large \Rightarrow ~~~ F_ {1 \rightarrow 3} \:=\: 0.28$$

حالا با جایگذاری این مقادیر در رابطه‌ای که برای اصل برهم‌نهی نوشتیم، $$\large F_ {1 \rightarrow \text {ring}}$$ به دست می‌آید.

$$\large F_ {1 \rightarrow \text {ring}} \:=\: F_ {1 \rightarrow 3} \:-\: F_ {1 \rightarrow 2} \:=\: 0.28 \:-\: 0.11 \:=\: 0.17$$

اصل تقارن

اگر هندسه مسئله، دارای تقارن باشد، محاسبه ضریب دید از این هم ساده‌تر خواهد شد. بنابراین، بهتر است پیش از اقدام به تعیین ضریب دید، وجود هرگونه تقارن در شکل مشخص شود. تشعشع خارج شونده از سطوح مشابهی که جهت‌گیری یکسانی دارند، رفتارشان نیز مشابه یکدیگر است. اصل تقارن به این صورت بیان می‌شود که اگر دو (یا چند) سطح، نسبت به سطح سوم، تقارن داشته باشند، ضریب دید مشابهی از آن سطح خواهند داشت. به شکل زیر دقت کنید.

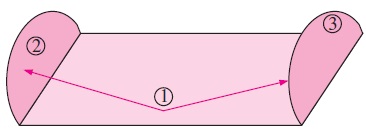
براساس این قانون، اگر سطوح $$\large j$$ و $$\large k$$ نسبت به سطح $$\large i$$ متقارن باشند، آنگاه رابطه $$\large F_ {i \rightarrow j} \:=\: F_ {i \rightarrow k}$$ برقرار خواهد بود. در این صورت، با استفاده از اصل تقابل می‌توان نشان داد که رابطه $$\large F_ {j \rightarrow i} \:=\: F_ {k \rightarrow i}$$ نیز صحیح است.

مثال ۳: محاسبه ضریب دید در یک هرم چهار وجهی

سؤال: ضریب دید از قاعده هرم چهاروجهی نشان داده شده در شکل زیر به هریک از چهار سطح جانبی را بیابید. قاعده هرم مربع بوده و هریک از سطوح جانبی آن، یک مثلث متساوی‌الساقین است.

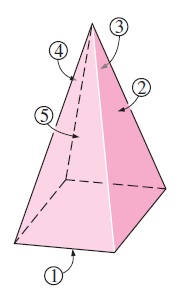
قاعده هرم (سطح شماره ۱) و هریک از چهار سطح جانبی آن (سطوح شماره ۲، ۳، ۴ و ۵) یک محفظه ۵ سطحی را تشکیل داده‌اند. اولین نکته‌ای که در بررسی این محفظه به چشم می‌]ورد، تقارن آن است. چهار سطح جانبی نسبت به قاعده هرم، تقارن دارند. بنابراین، اصل تقارن به شکل زیر نوشته می‌شود.

$$\large F_ {1 \rightarrow 2} \:=\: F_ {1 \rightarrow 3} \:=\:F_ {1 \rightarrow 4} \:=\:F_ {1 \rightarrow 5}$$

همچنین، استفاده از رابطه حاصل‌جمع، نتیجه زیر را در پی دارد.

$$\large \sum_{j=1}^5 F_{1j} \:=\: F_{11} \:+\: F_{12} \:+\: F_{13} \:+\: F_{14} \:+\: F_ {15} \:=\: 1$$

می‌دانیم مقدار $$\large F_{11} =0$$ برابر صفر است. در نتیجه، مقادیر ضریب دید به صورت زیر به دست می‌آید.

$$\large F_ {12} \:=\: F_ {13} \:=\:F_ {14} \:=\:F_ {15} \:=\: 0.25$$

همان‌طور که مشاهده کردید، هریک از سطوح جانبی هرم، یک چهارم تشعشع خارج شونده از سطح قاعده را دریافت کرد و استفاده از اصل تقارن، باعث شد محاسبات بسیار ساده‌تر انجام شود.

مثال ۴: محاسبه ضریب دید در یک مجرای مثلثی

سؤال: مجرای مثلثی نشان داده شده در شکل زیر را در نظر بگیرید که طول آن بی‌نهایت است. ضریب دید هریک از سطوح این مجرا را نسبت به سطح جانبی‌اش تعیین کنید.

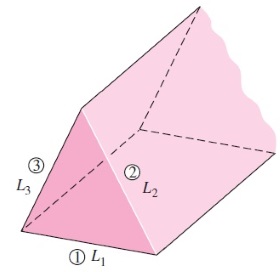
پاسخ: عرض سطوح جانبی این مجرای مثلثی برابر با $$\large L_1$$، $$\large L_2$$ و $$\large L_3$$ است. مساحت سطوح متناظر با این ابعاد را نیز به ترتیب برابر با $$\large A_1$$، $$\large A_2$$ و $$\large A_3$$ فرض می‌کنیم. از آنجایی که طول این مجرا تا بینهایت ادامه دارد، کسر تشعشع خارج‌شونده از هر سطح که از وجه انتهای مجرا می‌گریزد، قابل چشم‌پوشی است. بنابراین، این مجرا را به عنوان یک محفظه با سه سطح در نظر می‌گیریم ($$\large N=3$$). این محفظه دارای $$\large N^2 =9$$ ضریب دید است و تعداد ضرایب دیدی که باید مستقیماً محاسبه شود به صورت زیر مشخص می‌شود.

$$\large \frac {1} {2} N(N-1) \:=\: \frac {1} {2} \times 3(3-1) \:=\: 3$$

خوشبختانه رابطه زیر (با توجه به مسطح بودن هر سه سطح) برای یافتن این سه ضریب دید مجهول کفایت می‌کند.

$$\large F_{11} \:=\: F_ {22} \:=\: F_ {33} \:=\: 0$$

سایر ضرایب دید به راحتی و با به کارگیری اصل حاصل‌جمع و تقابل به دست می‌آیند. ابتدا اصل حاصل‌جمع را به هریک از سه سطح مجرا اعمال می‌کنیم.

$$\large F_{11} \:+\: F_ {12} \:+\: F_ {13} \:=\: 1 \\~\\ \large F_{21} \:+\: F_ {22} \:+\: F_ {23} \:=\: 1 \\~\\ \large F_{31} \:+\: F_ {32} \:+\: F_ {33} \:=\: 1$$

با استفاده از مقادیر به دست آمده و ضرب هریک از سطرها در مساحت سطح متناظرش، مجموعه رابطه‌های زیر به دست می‌آید.

$$\large A_1 F_{12} \:+\: A_1 F_{13} \:=\: A_1 \\~\\ \large A_2 F_{21} \:+\: A_2 F_{23} \:=\: A_2 \\~\\ \large A_3 F_{31} \:+\: A_3 F_{32} \:=\: A_3$$

حالا با نوشتن رابطه‌های تقابل، مجموعه روابط بالا را بازنویسی می‌کنیم.

$$\large A_1 F_{12} \:=\: A_2 F_{21} \\~\\ \large A_1 F_{13} \:=\: A_3 F_{31} \\~\\ \large A_2 F_{23} \:=\: A_3 F_{32} \\~\\ \large \Rightarrow ~~~ A_1 F_ {12} \:+\: A_1 F_ {13} \:=\: A_1 \\~\\ \large \Rightarrow ~~~ A_1 F_ {12} \:+\: A_2 F_ {23} \:=\: A_2 \\~\\ \large \Rightarrow ~~~ A_1 F_ {13} \:+\: A_2 F_ {23} \:=\: A_3$$

اکنون باید دستگاه معادلات سه معادله و سه مجهول بالا را حل کنیم.

$$\large F_ {12} \:=\: \frac {A_1 \:+\: A_2 \:-\: A_3} {2A_1} \:=\: \frac {L_1 \:+\: L_2 \:-\: L_3} {2L_1} \\~\\ \large F_ {13} \:=\: \frac {A_1 \:+\: A_3 \:-\: A_2} {2A_1} \:=\: \frac {L_1 \:+\: L_3 \:-\: L_2} {2L_1} \\~\\ \large F_ {23} \:=\: \frac {A_2 \:+\: A_3 \:-\: A_1} {2A_2} \:=\: \frac {L_2 \:+\: L_3 \:-\: L_1} {2L_2}$$

می‌توان این‌گونه نتیجه گرفت که ضریب دید از هر سطح یک مجرای مثلثی با طول بینهایت به سطح دیگر آن، برابر با حاصل‌جمع عرض این دو سطح منهای عرض سطح سوم، تقسیم به دو برابر عرض سطح اول است.

ضریب دید بین سطوحی با طول بینهایت: روش رشته‌های متقاطع

در بسیاری از مسئله‌های عملی با مواردی مواجه می‌شویم که در آنها یک کانال یا مجرا دارای سطح مقطع یکسان و طول بینهایت هستند. به عبارت دیگر، طول یک بُعد نسبت به دو بُعد دیگر،‌ به سمت بینهایت میل می‌کند. چنین شکل‌هایی را می‌توان دو بُعدی در نظر گرفت. ضریب دید در این موارد، با کمک روش بسیار ساده‌ای تعیین می‌شود که به روش رشته‌های متقاطع (Crossed Strings) معروف است. ضمناً دیگر نیازی نیست تا سطوح مورد نظر مسطح باشند و وجود هر گونه تحدب، تقعر یا هر بی‌نظمی دیگری ایجاد مشکل نخواهد کرد.

به شکل زیر توجه کنید. می‌خواهیم ضریب دید $$\large F_ {1 \rightarrow 2}$$ بین سطوح شماره ۱ و ۲ را مشخص کنیم. اولین کار، مشخص کردن نقاط ابتدا و انتهای هر سطح است. در اینجا نقاط $$\large A$$، $$\large B$$، $$\large C$$ و $$\large D$$ را مشخص می‌کنیم. سپس تمام این نقاط را با رشته‌های مستقیم به هم متصل می‌کنیم. می‌توان ثابت کرد که ضریب دید $$\large F_ {1 \rightarrow 2}$$ برحسب طول این رشته‌های مستقیم، قابل بیان است. برای این شکل، رابطه زیر برقرار خواهد بود.

$$\large F_ {1 \rightarrow 2} \:=\: \frac {(L_5 \: +\: L_6) \:-\: (L_3 \:+\: L_4)} {2L_1}$$

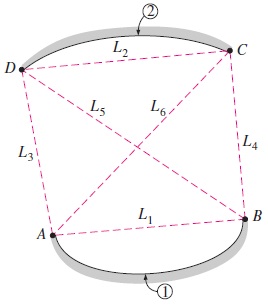
توجه کنید که عبارت $$\large (L_5 \:+\: L_6)$$ حاصل‌جمع طول رشته‌های متقاطع و $$\large (L_3 \:+\: L_4)$$ حاصل‌جمع طول رشته‌های غیر متقاطع است. مخرج کسر نیز طول رشته رسم شده روی سطح شماره ۱ است.

روش رشته‌های متقاطع، حتی هنگامی که دو سطح ۱ و ۲ دارای لبه مشترک باشند هم معتبر است. در این گونه موارد، لبه مشترک را رشته‌ای با طول صفر فرض می‌کنیم.

مثال ۵: روش رشته‌های متقاطع برای ضریب دید

سؤال: عرض دو صفحه موازی با طول بینهایت، به ترتیب برابر با $$\large a=12 cm$$ و $$\large b=5 cm$$ است. فاصله بین این دو صفحه را مطابق شکل زیر برابر با $$\large c=6 cm$$ در نظر بگیرید. الف) ضریب دید $$\large F_ {1 \rightarrow 2}$$ را با استفاده از روش رشته‌های متقاطع تعیین کنید. ب) با تشکیل مثلث‌هایی روی هندسه شکل و استفاده از رابطه به دست آمده در پاسخ مثال ۴، فرمول رشته‌های متقاطع را برای ضریب دید بین سطوح مثلث‌ها مشخص کنید.

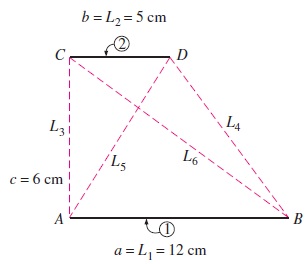
پاسخ: الف) ابتدا با استفاده از قانون رشته‌های متقاطع، ضریب دید $$\large F_ {1 \rightarrow 2}$$ را می‌یابیم.

$$\large L_1 \:=\: a \:=\: 12 \:cm ~ \Rightarrow ~ L_4 \:=\: \sqrt {7^2 \:+\: 6^2} \:=\: 9.22 \:cm \\~\\ \large L_2 \:=\: b \:=\: 5 \:cm ~ \Rightarrow ~ L_5 \:=\: \sqrt {5^2 \:+\: 6^2} \:=\: 7.81 \:cm \\~\\ \large L_3 \:=\: c \:=\: 6 \:cm ~ \Rightarrow ~ L_6 \:=\: \sqrt {12^2 \:+\: 6^2} \:=\: 13.42 \:cm \\~\\ \large F_ {1 \rightarrow 2} \:=\: \frac {(L_5 \:+\: L_6) \:-\: (L_3 \:+\: L_4)} {2L_1} \\~\\ \large F_ {1 \rightarrow 2} \:=\: \frac {\left[ \left( 7.81 \:+\: 13.42 \right) \:-\: \left( 6 \:+\: 9.22 \right) \right] cm} {2 \times 12 cm} \:=\: 0.250$$

ب) طول بُعد سوم در جهت عمود به صفحه و برابر با بینهایت است. از این رو، دو سطح ۱ و ۲ و دو سطح فرضی ۳ و ۴ یک محفظه چهار سطحی را تشکیل می‌دهند. اصل حاصل‌جمع را برای سطح شماره ۱ می‌نویسیم.

$$\large F_{11} \:+\: F_ {12} \:+\: F_ {13} \:+\: F_ {14} \:=\: 1 \\~\\ \large F_ {11} \:=\:0 \\~\\ \large \Rightarrow ~~~ F_ {12} \:=\: 1 \:-\: F_ {13} \:-\: F_ {14}$$

برای یافتن ضریب دید $$\large F_{13}$$ و $$\large F_{14}$$ باید مثلث‌های $$\large \text {ABC}$$ و $$\large \text {ABD}$$ را در نظر بگیریم. با مراجعه به پاسخ مثال شماره ۴، روابط زیر را برای این دو ضریب دید می‌نویسیم.

$$\large F_{13} \:=\: \frac {L_1 \:+\: L_3 \:-\: L_6} {2L_1} \\~\\ \large F_{14} \:=\: \frac {L_1 \:+\: L_4 \:-\: L_5} {2L_1}$$

حالا با جایگذاری این مقادیر در رابطه $$\large F_{12}$$، می‌توانیم مجهول را به دست آوریم.

$$\large F_{12} \:=\: 1\:-\: \frac {L_1 \:+\: L_3 \:-\: L_6} {2L_1} \:-\: \frac {L_1 \:+\: L_4 \:-\: L_5} {2L_1} \\~\\ \large \Rightarrow ~~~ F_ {12} \:=\: \frac {(L_5 \:+\: L_6) \:-\: (L_3 \:+\: L_4)} {2L_1}$$

همان‌طور که مشاهده می‌کنید، نتیجه به دست آمده، همان قانون رشته‌های متقاطع است. در صورت علاقه‌مندی به مباحث مرتبط در زمینه مهندسی مکانیک، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• انتقال حرارت تشعشعی — از صفر تا صد
• جسم سیاه در فیزیک — به زبان ساده
• تعریف گرما و دما در ترمودینامیک — به زبان ساده

^^