رگرسیون چند جمله ای — راهنمای کاربردی

روش‌های رگرسیونی برای مدل‌سازی داده‌ها بین متغیرهای مستقل و وابسته به کار می‌روند. در این بین مدل‌های رگرسیون خطی از محبوبیت زیادی برخوردار هستند. ولی گاهی استفاده از مدل رگرسیون خطی برای زمانی که ارتباط بین متغیر وابسته و مستقل روی یک خط راست قرار ندارد، نیز قابل استفاده است. رگرسیون چند جمله ای یکی از روش‌هایی است که با استفاده از یک چند جمله‌ای (Polynomial) برحسب متغیر مستقل، ارتباط با متغیر وابسته را مدل‌بندی می‌کند.

در این نوشتار با رگرسیون چند جمله ای و کاربردهای آن برای مدل‌سازی داده‌های زوجی یا چند بُعدی آشنا می‌شویم. همچنین به منظور نشان دادن عملکرد این نوع رگرسیون، با استفاده از یک مثال کاربردی با داده‌های واقعی، نحوه پیاده‌سازی آن را در زبان برنامه نویسی R، فرا می‌گیریم. برای آشنایی بیشتر با موضوع «رگرسیون خطی ساده» (Simple Regression) و «رگرسیون چندگانه» (Multiple Regression) نوشتارهای مختلفی در مجله فرادرس وجود دارد که خواندن آن‌ها را به شما توصیه می‌کنیم. برای مشاهده این مطالب بهتر است به لینک‌ آموزش رگرسیون — مجموعه مقالات جامع وبلاگ فرادرس مراجعه کنید. همچنین خواندن روش‌های رگرسیون در R — کاربرد در یادگیری ماشین (قسمت اول) و روش‌های رگرسیون در R — کاربرد در یادگیری ماشین (قسمت دوم) نیز برای آشنایی با نحوه کار با نرم‌افزار R برای تحلیل رگرسیونی، خالی از لطف نیست.

رگرسیون چند جمله ای

گاهی می‌توان یک مدل «غیرخطی» (Non-Linear) بین متغیرهای توصیفی و پاسخ را به صورت یک چند جمله‌ای درجه $$k$$ تعیین کرد. مدل «رگرسیونی چند جمله‌ای» (Polynomial Regression) در چنین مواقعی می‌تواند رابطه بین متغیرهای پیش‌گو و وابسته را به خوبی بیان کند.

فیلم آموزش درس رگرسیون 2 – جامع و کاربردی در فرادرس

کلیک کنید

می‌دانید که معادله یک خط راست توسط دو نقطه از آن خط، قابل تعیین است. در حقیقت در فضای اقلیدسی فقط یک خط راست وجود دارد که از دو نقطه می‌گذرد. همچنین برای مشخص کردن یک منحنی درجه ۲، کافی است سه نقطه از آن را بشناسیم تا معادله مربوط به آن را به همراه پارامترهای معادله مشخص و شکل آن را ترسیم کنیم.

هر چه تعداد نقاط بیشتر باشد، درجه منحنی یا چند جمله‌ای که از آن نقاط بگذرد، بیشتر خواهد شد. این طور به نظر می‌رسد که همیشه درجه منحنی یا چند جمله‌ای، یک واحد کمتر از تعداد نقاط است. در نتیجه اگر بخواهیم براساس ۱۰ نقطه یک منحنی برازش کنیم، به یک چندجمله‌ای نیازمندیم که درجه آن ۹ باشد. پیچیدگی در این مدل زیاد است زیرا چند جمله‌ای درجه ۹ دارای ۱۰ پارامتر است. یک رابطه یا تابع چند جمله‌ای مرتبه $$k$$ به صورت زیر نوشته می‌شود.

$$\large f(x) = a_0 + a_1 x+ a_2 x^2 + a_3 x^3 + \ldots + a_k x^k$$

رگرسیون چندجمله ای سعی دارد با استفاده از تعداد متغیرهای بسیار کمتر از تعداد نقطه‌ها، پارامترهای چند جمله‌ای یا رگرسیون را برآورد کند. در نتیجه پیچیدگی مدل کاهش یافته ولی در عوض خطا نیز بوجود خواهد آمد. به این ترتیب یک توازن بین بیش‌برازش (Overfitting) و کم‌برازش (Underfitting) در مدل برقرار خواهد شد.

طبق قضیه یا بسط تیلور می‌توانیم هر «تابع پیوسته» (continuous function)  و دارای مشتقات متعدد را به صورت یک رابطه خطی یا چند جمله‌ای نمایش دهیم. همین جنبه، ما را به سوی رگرسیون چند جمله‌ای سوق می‌دهد.

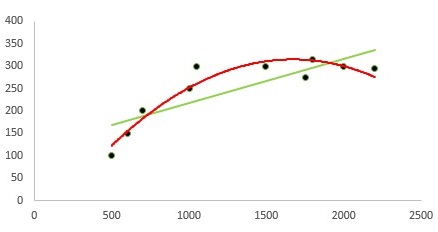
در تصویر زیر چنین حالتی را مشاهده می‌کنید. خط سبز رنگ، مدل رگرسیون خطی و خط قرمز رنگ، مدل چندجمله‌ای مرتبه ۲ را نشان می‌دهد. این طور که به نظر می‌رسد، منحنی قرمز رنگ، بهتر توانسته است تغییرات متغیر پاسخ را نشان دهد.

به این ترتیب می‌توان مدل رگرسیون خطی زیر را برای رگرسیون چند جمله ای در نظر گرفت.

$$\large y = \beta_0 + \beta_1 X + \beta_2 X^2 + \ldots + \beta_k X^k + \epsilon$$

رابطه ۱

بر همین اساس می‌توان رگرسیون چندجمله‌ای را به صورت رگرسیون خطی چندگانه و به شکل زیر درج کرد.

$$\large X_1 = X , \; \; X_2 = X^2, \; \; \ldots , \; \; X_k = X^k$$

نکته: اگر درجه چند جمله‌ای را برابر با تعداد مشاهدات قرار دهیم ($$n=k$$) با مشکل بیش‌برازش (Overfitting) مواجه خواهیم شد.

اجرای رگرسیون چند جمله ای در R

برای اجرای رگرسیون چند جمله‌ای از یک فایل داده به نام poly.csv استفاده می‌کنیم که شامل مساحت و قیمت خانه‌ها است. قرار است به کمک مدل رگرسیونی بتوانیم براساس مساحت خانه‌ها، قیمت آن‌ها را پیش‌بینی کنیم.

فیلم آموزش برنامه نویسی R و نرم افزار RStudio – مقدماتی در فرادرس

کلیک کنید

کدهای زیر به منظور اجرای رگرسیون چند جمله‌ای براساس متغیر وابسته قیمت (Price) و متغیر مستقل مساحت (Area) ایجاد شده است. برای دسترسی به اطلاعات این فایل می‌توانید آن را به صورت فشرده و در قالب متنی از اینجا دریافت کنید و پس از خارج کردن از حالت فشرده، با دستور read.csv در R بخوانید.

نکته: فایل‌هایی با قالب csv به عنوان جدول‌های اطلاعاتی در نظر گرفته می‌شوند که اقلام یا ستون‌های مقادیر آن با علامت کاما (,) از یکدیگر جدا شده‌اند. عبارت csv مخفف عبارت comma separated value است.

1data = read.csv("poly.csv")
2x = data$Area
3y = data$Price

به منظور مقایسه مدل رگرسیون خطی ساده و مدل چند جمله‌ای، دو بار از تابع lm که عمل برازش مدل رگرسیون خطی را انجام می‌دهد استفاده می‌کنیم. در حالت اول، نتیجه مدل را در متغیر model1 ذخیره کرده و زمانی که از رگرسیون چند جمله‌ای بامرتبه ۲ استفاده می‌کنیم، خروجی را در متغیر model2 ذخیره خواهیم کرد.

1model1 = lm(y ~x)
2model1$fit
3model1$coeff
4
5new_x = cbind(x,x^2)
6model2 = lm(y~new_x)
7model2$fit
8model2$coeff

نتیجه حاصل از اجرای کدها و ساخت مدل به صورت زیر خواهد بود.

1> model1$fit
2       1        2        3        4        5        6        7        8        9       10 
3169.0995 178.9081 188.7167 218.1424 223.0467 266.6949 291.7068 296.6111 316.2282 335.8454 
4> model1$coeff
5 (Intercept)            x 
6120.05663769   0.09808581 
7
8
9> model2$fit
10       1        2        3        4        5        6        7        8        9       10 
11122.5388 153.9997 182.6550 251.7872 260.8543 310.6514 314.1467 312.6928 299.8631 275.8110 
12> model2$coeff
13  (Intercept)        new_xx         new_x 
14-7.684980e+01  4.689175e-01 -1.402805e-04

همانطور که می‌بینید در model1، مقدار عرض از مبدا (Intercept) برابر با 0٫098 و در model2 برابر با 76.84- است. از طرفی ضریب مساحت (متغیر $$x$$) در مدل اول برابر با 120٫057 و در مدل دوم نیز 0٫04689 است. متغیر دوم ($$x^2$$) فقط در مدل دوم وجود دارد و مقدار آن برابر با 0٫00014- است.

در نتیجه مدل‌های اول و دوم به صورت زیر نوشته خواهند شد:

$$\large \text{Model1 : } Price = 0.098 + 120.057 \times Area$$

$$\large \text{Model2 : } Price = -76.84 + 0.04689 \times Area - 0.00014 \times Area^2$$

همچنین برای نمایش نحوه برازش مدل‌های رگرسیون یاد شده از نموداری استفاده می‌کنیم که نقاط و همچنین مقادیر برازش شده در هر دو مدل را با هم ترسیم می‌کند. کدهای انجام این کار با استفاده از بسته یا کتابخانه ggplot2 در ادامه قابل مشاهده است.

نکته: کتابخانه ggplot2 شامل توابع و ابزارهایی است که امکان ترسیم نمودارها را به صورت پیچیده فراهم می‌آورد. اگر این کتابخانه روی نرم‌افزار R، نصب نشده است، ابتدا با دستور Install.package، آن را بارگذاری کرده سپس برنامه زیر را اجرا کنید.

1library(ggplot2)
2<p style="direction: rtl;">ggplot(data = data) + geom_point(aes(x = Area,y = Price)) +<br></p>geom_line(aes(x = Area,y = model1$fit),color = "red") +
3geom_line(aes(x = Area,y = model2$fit),color = "blue") +
4theme(panel.background = element_blank())

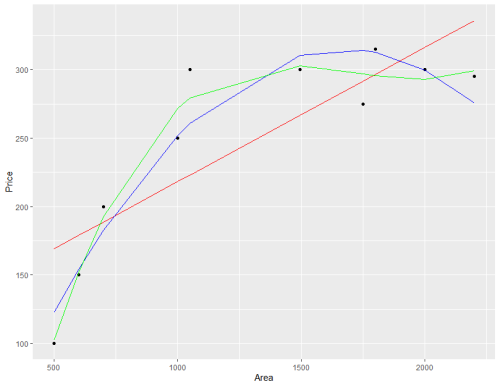
نتیجه اجرای این قطعه کد، به صورت نموداری است که در ادامه مشاهده می‌کنید. محور افقی در اینجا مساحت و محور عمودی مربوط به قیمت خانه‌ها است.

نقاط سیاه رنگ، مقادیر واقعی است که برحسب مساحت و قیمت خانه‌ها ترسیم شده. خط قرمز رنگ، نمایانگر رابطه رگرسیون خطی است که براساس این داده‌ها برازش داده شده. همچنین خطوط شکسته به رنگ آبی هم، مدل رگرسیون چند جمله‌ای به فرم درجه ۲ است که بهتر توانسته نقاط اصلی را مدل‌بندی کند. همانطور که مشاهده می‌کنید، مجموع فاصله این منحنی نسبت به نقاط سیاه رنگ، کمتر از خط قرمز رنگ بوده، پس مدل رگرسیونی درجه دوم بهتر عمل کرده است.

فیلم آموزش تحلیل رگرسیون لجستیک دو حالتی در SPSS اس پی اس اس در فرادرس

کلیک کنید

نکته: می‌توان، مدل رگرسیون چند جمله‌ای برای این مثال را با درجه یا مرتبه سه نیز انجام داد ولی تعداد پارامترها و در نتیجه پیچیدگی مدل افزایش می‌یابد. کد مربوط به این وضعیت برای چند جمله‌ای درجه ۳ و نتیجه حاصل، در ادامه قابل مشاهده است.

1new3_x = cbind(x,x^2,x^3) 
2model3 = lm(y~new3_x)
3model3$fit 
4model3$coeff
5
6
7
8ggplot(data = data) + geom_point(aes(x = Area,y = Price)) +geom_line(aes(x = Area,y = model1$fit),color = "red") +
9  geom_line(aes(x = Area,y = model2$fit),color = "blue") +geom_line(aes(x = Area,y = model3$fit),color = "green")
10  theme(panel.background = element_blank())

خروجی به شکل زیر است.

1> model3$fit 
2       1        2        3        4        5        6        7        8        9 
3102.1521 151.7131 192.6506 271.4791 279.2208 302.8341 296.9721 295.6443 293.0125 
4      10 
5299.3213 
6> model3$coeff
7  (Intercept)       new3_xx        new3_x        new3_x 
8-3.021495e+02  1.108212e+00 -6.638514e-04  1.292679e-07

البته در این قسمت مشاهده می‌کنید که مقدار برازش شده برای هر سه مدل نیز با یکدیگر مقایسه شده‌اند. اختلاف بین مقدار پیش‌بینی شده در مدل اول با مدل‌های دیگر بسیار زیاد است در حالیکه بین مدل درجه دوم و سوم، تغییرات پیش‌بینی یا خطا خیلی چشم‌گیر نیست.

1> model1$fit 
2       1        2        3        4        5        6        7        8        9 
3169.0995 178.9081 188.7167 218.1424 223.0467 266.6949 291.7068 296.6111 316.2282 
4      10 
5335.8454 
6> model2$fit 
7       1        2        3        4        5        6        7        8        9 
8122.5388 153.9997 182.6550 251.7872 260.8543 310.6514 314.1467 312.6928 299.8631 
9      10 
10275.8110 
11> model3$fit 
12       1        2        3        4        5        6        7        8        9 
13102.1521 151.7131 192.6506 271.4791 279.2208 302.8341 296.9721 295.6443 293.0125 
14      10 
15299.3213

نمودار مربوط به نقاط برازش شده نیز به صورت زیر ترسیم می‌شود.

مزایا و معایب استفاده از رگرسیون چند جمله ای

برآورد پارامترهای رگرسیون چند جمله ای، معمولا به وسیله روش‌های آزمون و خطا یا بهینه‌سازی صورت می‌گیرد و در طی تکرار یک فرآیند، جواب‌های مناسب حاصل می‌شوند. روش‌های محاسبات عددی مانند گرادیان کاهشی (Gradient Descent) و تکنیک‌های درون‌یابی (Interpolation Techniques) در این گونه مواقع به کار می‌روند.

فیلم آموزش محاسبات عددی – مرور و حل مساله در فرادرس

کلیک کنید

به هر حال مزایا و معایب رگرسیون چند جمله ای را می‌توان به صورت زیر برشمرد.

مزایا

• رگرسیون چند جمله ای بهترین مدل تقریبی را بین متغیر وابسته و مستقل پیدا می‌کند.
• بسیاری از توابع پیچیده غیر خطی، توسط رگرسیون چند جمله ای قابل برازش هستند.
• همگرایی به پاسخ بهینه در اغلب موارد با سرعت زیاد همراه است.

معایب

• وجود داده‌های پرت (Outlier) باعث گمراه شدن مدل و در نتیجه نامعتبر بودن مقدار برازش شده، خواهد شد.
• متاسفانه شناسایی داده‌ پرت در مدل‌های غیرخطی پیچیده و مشکل‌تر از مدل‌های خطی است که این امر بکارگیری رگرسیون چند جمله ای را محدود می‌کند.

خلاصه و جمع‌بندی

در این نوشتار با رگرسیون چند جمله‌ای به عنوان ابزاری برای تبدیل رابطه غیر خطی به یک مدل رگرسیونی آشنا شدیم. همانطور که دیدید، ممکن است این مدل براساس متغیر مستقل و وابسته به صورت یک رابطه غیرخطی در نظر گرفته شود ولی آنچه در مدل رگرسیونی به عنوان مدل غیرخطی شناخته می‌شود، رابطه بین پارامترها است. از آنجایی که بین پارامترهای متغیرها در اینجا عمل جمع یا تفریق صورت می‌گیرد، باز هم مدل رگرسیون چند جمله ای را به عنوان یک روش یا مدل خطی (Linear Model) در نظر می‌گیریم.