خواص ماتریس ها — به زبان ساده

پیش‌تر در مجموعه آموزش‌های ریاضی مجله فرادرس، با ماتریس آشنا شدیم. در این آموزش‌، برخی از مهم‌ترین خواص ماتریس ها را بیان می‌کنیم که کاربردهای فراوانی در جبر خطی دارند.

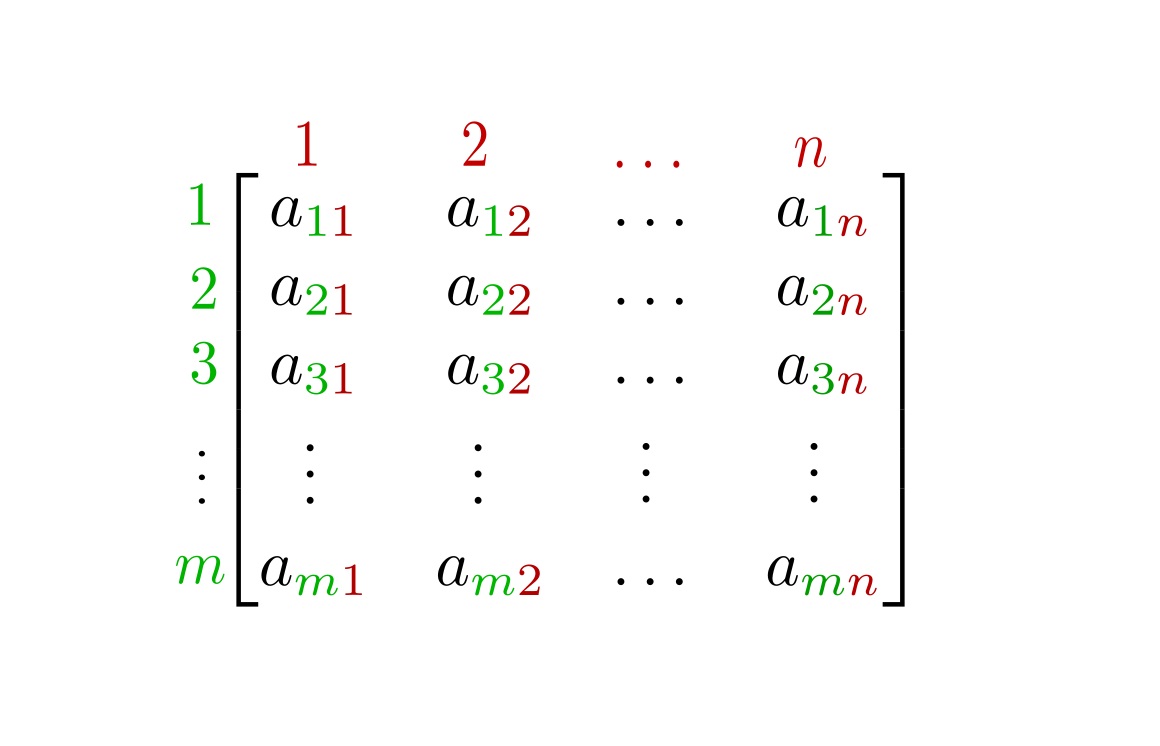
۱. ماتریس $$A$$ با بعد $$m \times n$$ یک آرایه مستطیلی از درایه‌ها یا عناصر $$a _ { i j }$$، شامل $$m$$ سطر و $$n$$ ستون است.

$$ \large A = \left [ { { a _ { i j } } } \right ] = \left [ { \begin {array} { * { 2 0 } { c } }<br /> { { a _ { 1 1 } } } & { { a _ { 1 2 } } } & \ldots & { { a _ { 1 n} } } \\<br /> { { a _ { 2 1 } } } & { { a _ { 2 2 } } } & \ldots & { { a _ { 2 n } } } \\<br /> \vdots & \vdots & { } & \vdots \\<br /> { { a _ { m 1 } } } & { { a _ { m 2 } } } & \ldots & { { a _ { m n } } }<br /> \end {array} } \right ] $$

فیلم آموزش هندسه 3 – پایه دوازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

۲. یک ماتریس مربعی مرتبه $$n$$ دارای $$n$$ سطر و $$n$$ ستون است.

۳. ماتریس مربعی $$\left[ {{a_{ij}}} \right]$$ را یک ماتریس متقارن می‌نامیم اگر $$a _ { i j } = a _ { j i }$$ باشد، یعنی درایه‌های ماتریس نسبت به قطر اصلی متقارن باشند.

۴. ماتریس مربعی $$\left[ {{a_{ij}}} \right]$$ پادمتقارن است اگر $$a _ { i j } = - a _ { j i }$$.

۵. یک ماتریس مربعی، قطری نامیده می‌شود اگر همه دریایه‌های غیر از قطر اصلی آن صفر باشند.

۶. یک ماتریس قطری، همانی نامیده می‌شود اگر درایه‌های روی قطر اصلی آن برابر با ۱ باشند.

۷. ماتریسی که همه درایه‌های آن برابر با صفر باشند، یک ماتریس صفر یا ماتریس پوچ نامیده می‌شود.

۸. دو ماتریس $$A$$ و $$B$$ با هم برابرند اگر و تنها اگر اندازه مشابه $$m \times n$$ داشته باشند و درایه‌های متناظر آن‌ها با هم برابر باشد.

۹. دو ماتریس $$A$$ و $$B$$ را می‌توان با هم جمع (یا از هم تفریق) کرد اگر و تنها اگر اندازه $$m \times n$$ آن‌ها برابر باشد. اگر

$$ \large A = \left [ { { a _ { i j } } } \right ] = \left[ { \begin {array} { * { 2 0 } { c } }<br /> { { a _ { 1 1 } } } & \ldots & { { a _ { 1 n } } } \\<br /> { { a _ { 2 1 } } } & \ldots & { { a _ { 2 n } } } \\<br /> \vdots & { } & \vdots \\<br /> { { a _ { m 1 } } } & \ldots & { { a _ { m n } } }<br /> \end {array} } \right ] , \; \left [ { \begin {array} { *{ 2 0 } { c } }<br /> { { b _ { 1 1 } } } & \ldots & { { b _ { 1 n } } } \\<br /> { { b _ { 2 1 } } } & \ldots & { { b _ { 2 n } } } \\<br /> \vdots & { } & \vdots \\<br /> { { b _ { m 1 } } } & \ldots & { { b _ { mn } } }<br /> \end {array} } \right ] , $$

آن‌گاه، جمع این دو ماتریس برابر است با:

$$ \large A + B = \left [ { \begin {array} { * { 2 0 } { c } }<br /> { { a _ { 1 1} } + { b _ { 1 1 } } } & \ldots & { { a _ { 1 n } } + { b _ { 1 n } } } \\<br /> { { a _ { 21 } } + { b _ { 2 1 } } } & \ldots & { { a _ { 2 n } } + { b _ { 2 n } } } \\<br /> \vdots & { } & \vdots \\<br /> { { a _ { m 1 } } + { b _ { m 1 } } } & \ldots & { { a _ { m n } } + { b _ { m n } } }<br /> \end {array} } \right ] $$

۱۰. عدد ثابت $$k$$ و ماتریس $$A = \left[ {{a_{ij}}} \right]$$ داده شده‌اند. آنگاه، ضرب آن‌ها به صورت زیر خواهد بود:

$$ \large k A = \left [ { { k a _ { i j } } } \right ] = \left [ { \begin {array} { * { 2 0 } { c } }<br /> { { k a _ { 1 1 } } } & { { k a _ { 1 2 } } } & \ldots & { { k a _ { 1 n } } } \\<br /> { { k a _ { 2 1 } } } & { { k a _ { 2 2 } } } & \ldots & { { k a _ { 2 n } } } \\<br /> \vdots & \vdots & {} & \vdots \\<br /> { { k a _ { m 1 } } } & { { k a _ { m 2 } } } & \ldots & { { k a _ { m n } } }<br /> \end {array} } \right ] . $$

۱۱. فرض کنید $$A$$ و $$B$$ دو ماتریس باشند. ضرب ماتریس‌های $$AB$$ وجود دارد اگر و تنها اگر تعداد ستون‌های ماتریس اول برابر با تعداد سطرهای ماتریس دوم باشد. اگر ماتریس‌های $$A$$ و $$B$$ به صورت زیر باشند:

$$ \large A = \left [ { { a _ { i j } } } \right ] = \left [ { \begin {array} { * { 2 0 } { c } }<br /> { { a _ { 1 1 } }} & { { a _ { 1 2 } } } & \ldots & { {a _ { 1 n } } } \\<br /> { { a _ { 2 1 } } } & { { a _ { 2 2 } } } & \ldots & { { a _ { 2 n } } } \\<br /> \vdots & \vdots & { } & \vdots \\<br /> { { a _ { m 1 } } } & { { a _ { m 2 } } } & \ldots & { { a _ { m n } } }<br /> \end {array} } \right ] , \; B = \left [ { { b _ { i j } } } \right ] = \left [ { \begin {array} { * { 2 0 } { c } }<br /> { { b _ { 1 1 } } } & { { b _ { 1 2 } } } & \ldots & { { b _ { 1 k } } } \\<br /> { { b _ { 2 1 } } } & { { b _ { 2 2 } } } & \ldots & {{ b _ { 2 k } } } \\<br /> \vdots & \vdots & { } & \vdots \\<br /> { { b _ { n 1 } } } & { { b _ { n 2 } } } & \ldots & { { b _ { n k } } }<br /> \end {array} } \right ] , $$

آنگاه ضرب $$A B$$ با ماتریس زیر نشان داده می‌شود:

$$ \large AB = C = \left [ { \begin {array} { * { 2 0 } { c } }<br /> { { c _ { 1 1 } } } & { { c _{ 1 2 } } } & \ldots & { { c _ { 1 k } } } \\<br /> { { c _ { 2 1 } } } & { { c _ { 2 2 } } } & \ldots & { { c _ { 2 k } }} \\<br /> \vdots & \vdots & { } & \vdots \\<br /> { { c _ { m 1 } } } & { { c _ { m 2 } } } & \ldots & { { c _ { m k } } }<br /> \end {array} } \right ] , $$

که در آن، درایه‌های ماتریس $$C$$ به صورت زیر تعریف می‌شوند:

$$\large { c _ { i j } } = { a _ { i 1 } } { b _ { 1 j } } + { a _ { i 2 } } { b _ { 2 j } } + \ldots + \; { a _ { i n } } { b _ { nj } } = \sum \limits _ { \lambda = 1 } ^ n { { a _ { i \lambda }}{ b _ { \lambda j } } } , \; \\ \big( {i = 1,2, \ldots ,m,}\; {j = 1,2, \ldots ,k} \big)$$

برای مثال، اگر داشته باشیم:

$$ \large A = \left [ { { a _ { i j } } } \right ] = \left [ { \begin {array} { * { 2 0 } { c } }<br /> { { a _ { 1 1 } } } & { {a _ { 1 2 } } } & { {a _ { 1 3 } } } \\<br /> { { a _ { 2 1 } } } & { { a _ { 2 2 } } } & {{ a _ { 3 1 } } }<br /> \end {array} } \right ] , \; B = \left [ { { b _ i } } \right ] = \left [ { \begin {array} { * { 2 0 } {c } }<br /> { { b _ 1 } } \\<br /> { { b _ 2 } } \\<br /> { { b _ 3 } }<br /> \end {array} } \right ] , $$

آنگاه ضرب $$AB$$ به صورت زیر خواهد بود:

$$ \large A B = \left [ { \begin {array} { * { 2 0 } { c } }<br /> { { a _ { 1 1 } } } & { { a _ { 1 2 } } } & { { a _ { 1 3 } } } \\<br /> { { a _ {2 1 } } } & { { a _ { 2 2 } }} & { {a _ { 3 1 } }}<br /> \end {array} } \right ] \cdot \left [ { \begin {array} { * { 2 0 } { c } }<br /> { { b _ 1 } } \\<br /> { { b _ 2 } } \\<br /> { { b _ 3 } }<br /> \end {array} } \right ] = \left [ { \begin {array} { * { 2 0 }{ c } }<br /> { { c _ { 1 1 } } } \\<br /> { { c _ { 2 1 } } }<br /> \end {array} } \right ] = \left [ { \begin {array} { * { 2 0 } {c } }<br /> { { a _ { 1 1 } } { b _ 1 } + { a _ { 1 2 } } { b _ 2 } + { a _ { 1 3 } } { b _ 3 } } \\<br /> { { a _ { 2 1 } } {b _ 1 } + { a _ { 2 2 } } { b _ 2 } + { a _ {2 3 } } { b _ 3 } }<br /> \end {array} } \right ] . $$

۱۲. اگر سطرها و ستون‌های یک ماتریس را با هم تعویض کنیم، ماتریس جدید ترانهاده ماتریس اصلی نامیده می‌شود. ترانهاده ماتریس $$A$$‌ با $$A ^T$$ نشان داده می‌شود.

۱۳ ماتریس $$A$$ را متعامد می‌نامیم اگر $$AA^T = I$$ باشد، که $$I$$ ماتریس همانی است.

۱۴. اگر ضرب ماتریسی $$AB$$ تعریف شده باشد، آنگاه $$( A B) ^T = B ^T A ^ T$$.

۱۵. اگر $$A$$ یک ماتریس مربعی مرتبه $$n$$ باشد، آنگاه ماتریس الحاقی متناظر که با $$C ^*$$ نشان داده می‌شود، ماتریسی است که با همسازه‌های $$A _ { i j }$$ درایه‌های ترانهاده $$A ^ T$$ ماتریس تشکل شده است.

۱۶. اگر $$A$$ یک ماتریس مربعی مرتبه $$n$$ باشد، آنگاه اثر آن که با $$\text{tr }A$$ نشان داده می‌شود، برابر با مجموع درایه‌های روی قطر اصلی است:‌

$$\large \text {tr } A = { a _ { 1 1 } } + { a _ {2 2 } } + { a _ {3 3 } } + \ldots + \; { a _ { n n } } .$$

۱۷. معکوس ماتریس $$A$$ را با $$A ^ { - 1 }$$ نشان می‌دهیم. این ماتریس به گونه‌ای است که حاصل‌صرب ماتریس اصلی $$A$$ در معکوس $$A ^ { - 1 }$$ برابر با ماتریس همانی $$I$$ خواهد بود: $$A A ^ { - 1 } = I$$.

معکوس یک ماتریس تنها برای ماتریس‌های نامنفرد مربعی (دترمینان آن‌ها غیرصفر است) تعریف می‌شود. اگر $$A$$ یک ماتریس نامنفرد مربعی مرتبه $$n$$ باشد، معکوس ماتریس $$A ^ { - 1 }$$ به صورت زیر بیان می‌شود:

$$\large { A ^ { – 1 } } = { \large \frac { { { C ^ * } } } { { \det A } } \normalsize } ,$$

که در آن، $$C ^*$$ الحاقی و $$\det A$$ دترمینان ماتریس $$A$$ هستند.

۱۸. اگر ضرب ماتریس $$AB$$ تعریف شده باشد، آنگاه:

$$\large {\left( {AB} \right)^{ – 1}} = {B^{ – 1}}{A^{ – 1}}$$

۱۹. اگر $$A$$ یک ماتریس مربعی باشد، بردارهای ویژه $$X$$ در معادله ماتریسی زیر صدق می‌کنند:

$$\large AX = \lambda X$$

و مقادیر ویژه $$\lambda$$ از معادله مشخصه زیر به دست می‌آیند:

$$\large AX = \lambda X$$

اگر علاقه‌مند به یادگیری مباحث مشابه مطلب بالا هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس ریاضیات
• آموزش جبر خطی با متلب
• مجموعه آموزش‌های مهندسی کنترل
• آموزش کنترل مدرن به همراه پیاده سازی در متلب​‎
• تجزیه مقادیر منفرد (SVD) — به زبان ساده
• خواص دترمینان — به زبان ساده
• تقلب نامه (Cheat Sheet) جبر خطی برای یادگیری ماشین — راهنمای سریع و کامل

^^