حل انتگرال با قضیه مانده – از صفر تا صد

در ادامه مجموعه آموزش‌های ریاضی مجله فرادرس، در این آموزش روش حل انتگرال با قضیه مانده را بررسی می‌کنیم.

حل انتگرال با قضیه مانده

از قضیه مانده برای محاسبه انتگرال‌های معین حقیقی به شکل زیر استفاده خواهیم کرد:

$$\large \int _ a ^ b f ( x ) d x$$

روش کلی محاسبه انتگرال معین با استفاده از روش مانده به صورت زیر است:

1. یافتن یک تابع مختلط تحلیلی $$g ( z )$$ که روی محور حقیقی برابر با $$f$$ است یا با $$f$$ ارتباط نزدیکی دارد؛ برای مثال، $$f ( x ) = \cos (x)$$ و $$g ( z ) = e ^ { i z }$$.
2. انتخاب کانتور بسته $$C$$ که شامل بخش محور حقیقی در انتگرال است.
3. کانتور از بخش‌هایی تشکیل شده است. باید بتوان $$\int g ( z ) d z$$ را برای هر بخش، جز روی محور حقیقی، محاسبه کرد.
4. استفاده از قضیه مانده برای محاسبه $$\int _ C g ( z ) d z$$.
5. ترکیب مراحل قبل برای به دست آوردن مقدار انتگرال.

محاسبه انتگرال توابع نزولی

قضایای این بخش به ما در انتخاب کانتور $$C$$ کمک خواهند کرد. قضیه اول برای توابعی است که با سرعت بیشتر از $$1/ z$$ نزولی هستند.

قضیه ۱: (الف) فرض کنید $$f ( z )$$ در نیم‌صفحه بالایی تعریف شده است. اگر یک $$a > 1$$ و $$M > 0$$ وجود داشته باشند که برای $$|z |$$ بزرگ داشته باشیم:

$$\large | f ( z ) | < \frac { M} { |z| ^ a }$$

آنگاه، داریم:

$$\lim _ { R \to \infty } \int _ { C_ R} f ( z ) d z = 0$$

که در آن، $$C _ R$$ نیم‌دایره سمت چپ شکل ۱ است.

$$R e ^ { i \theta} , 0 < \theta < \pi$$ و نیم‌دایره سمت راست: $$R e ^ { i \theta} , \pi < \theta < 2\pi$$" width="557" height="141">

(ب) اگر $$f ( z )$$ در نیم‌صفحه پایینی تعریف شده و برای $$a > 1$$، داشته باشیم:

$$\large | f ( z ) | < \frac{ M } { |z| ^ a }$$

آنگاه:

$$\large \lim _ { R \to \infty} \int _ { C_R} f ( z) d z = 0 ,$$

که در آن، $$C _ R$$ نیم‌دایره سمت راست شکل بالا است.

اثبات:‌ (الف) و (ب) را به طور مشابه اثبات می‌کنیم. از نامساوی مثلثی برای انتگرال و تخمین مفروض استفاده می‌کنیم. برای $$R$$ بزرگ، داریم:

$$\large \left | \int _ { C _ { R } } f ( z ) d z \right | \leq \int _ { C _ { R } } | f ( z ) | | d z | \leq \int _ { C _ { R } } \frac { M } { | z | ^ { a } } | d z | = \int _ { 0 } ^ { \pi } \frac { M } { R ^ { a } } R d \theta = \frac { M \pi } { R ^ { a - 1 } }$$

از آنجا که $$a > 1$$ است، واضح است که وقتی $$R \to \infty$$، آنگاه عبارت بالا به صفر میل می‌کند.

قضیه بعدی برای توابعی است که مانند $$1 / z$$ کاهش می‌یابند.

قضیه ۲: (الف) فرض کنید $$f ( z )$$ در نیم‌صفحه بالایی تعریف شده باشد. اگر برای $$|z|$$ بزرگ $$M > 0$$ به گونه‌ای وجود داشته باشد که

$$\large | f ( z ) | < \frac { M } { | z | }$$

آنگاه برای $$a > 0$$، داریم:

$$\large \lim _ { x _ { 1 } \rightarrow \infty , x _ { 2 } \rightarrow \infty } \int _ { C _ { 1 } + C _ { 2 } + C _ { 3 } } f ( z ) \mathrm { e } ^ { i a z } d z = 0$$

که در آن، $$C _ 1 + C_ 2 + C_ 3$$ مسیر مستطیلی سمت چپ شکل زیر است.

$$x_ 1 + x _ 2$$" width="563" height="137">

(ب) به طور مشابه، اگر $$a < 1$$ باشد، آنگاه

$$\large \lim _ { x _ { 1 } \rightarrow \infty , x _ { 2 } \rightarrow \infty } \int _ { C _{ 1 } + C _ { 2 } + C _ { 3 } } f ( z ) \mathrm { e } ^ { i a z } d z = 0$$

که در آن، $$C _ 1 + C_ 2 + C_ 3$$ مسیر مستطیلی سمت راست شکل بالا است.

توجه کنید که برای تفکیل قضیه ۱ از این قضیه، باید عامل $$e ^ { i a z }$$ را در نظر بگیریم.

اثبات: (الف) با پارامتری کردن $$C_ 1$$، $$C_ 2$$ و $$C_ 3$$ شروع می‌کنیم.

• $$C_1$$: $$\gamma _ 1 ( t) = x_ 1 + i t$$ و $$t$$ از $$0$$ تا $$x _ 1 + x_ 2$$.
• $$C_2$$: $$\gamma _ 2 ( t) = t + i (x _ 1 + x_ 2 )$$ و $$t$$ از $$x_1$$ تا $$- x_ 2$$.
• $$C_3$$: $$\gamma _ 3 ( t) = -x_ 2 + i t$$ و $$t$$ از $$x_1+x_2$$ تا $$0$$.

در ادامه هر یک از انتگرال‌ها را بررسی می‌کنیم. فرض می‌کنیم $$x _ 1$$ و $$x _ 2$$ به اندازه کافی بزرگ باشند، به طوری که روی هر منحنی $$C_ i$$:

$$\large | f ( z ) | < \frac { M } { | z | }$$

$$\large \begin {aligned} \left | \int _ { C _ { 1 } } f ( z ) \mathrm { e } ^ { i a z } d z \right | & \leq \int _ { C _ { 1 } } \left | f ( z ) \mathrm { e } ^ { i a z } \right | | d z | \leq \int _ { C _ { 1 } } \frac { M } { | z | } \left | \mathrm { e } ^ { i a z } \right | | d z | \\ & = \int _ { 0 } ^ { x _ { 1 } + x _ { 2 } } \frac { M } { \sqrt { x _ { 1 } ^ { 2 } + t ^ { 2 } } } \left | \mathrm { e } ^ { i a x _ { 1 } - a t } \right | d t \\ & \leq \frac { M } { x _ { 1 } } \int _ { 0 } ^ { x _ { 1 } + x _ { 2 } } \mathrm { e } ^ { - a t } d t \\ & = \frac { M } { x _ { 1 } } \left ( 1 - \mathrm { e } ^ { -a \left ( x _ { 1 } + x _ { 2 } \right ) } \right ) / a \end {aligned}$$

از آنجا که $$a > 0$$ است، واضح است که عبارت آخر با رفتن $$x _ 1$$ و $$x _ 2$$ به $$\infty$$، به $$0$$ میل خواهد کرد.

$$\large \begin {aligned} \left | \int _ { C _ { 2 } } f ( z ) \mathrm { e } ^ { i a z } d z \right | & \leq \int _ { C _ { 2 } } \left | f ( z ) \mathrm { e } ^ { i a z } \right | | d z | \leq \int _ { C _ { 2 } } \frac { M } { | z | } \left | \mathrm { e } ^ { i a z } \right | | d z | \\ & = \int _ { - x _ { 2 } } ^ { x _ { 1 } } \frac { M } { \sqrt { t ^ { 2 } + \left ( x _ { 1 } + x _ { 2 } \right ) ^ { 2 } } } \left | \mathrm { e } ^ { i a t -a \left ( x _ { 1 } + x _ { 2 } \right ) } \right | d t \\ & \leq \frac { M \mathrm { e } ^ { - a \left ( x _ { 1 } + x _ { 2 } \right ) } } { x _ { 1 } + x _ { 2 } } \int _ { 0 } ^ { x _ { 1 } + x _ { 2 } } d t \\ & \leq M \mathrm { e } ^ { - a \left ( x _ { 1 } + x _ { 2 } \right ) } \end {aligned}$$

مجدداً واضح است که وقتی $$x _ 1$$ و $$x _ 2$$ به بینهایت بروند، آنگاه عبارت آخر به صفر میل می‌کند. اثبات برای $$C_ 3$$ اساساً مشابه ‌$$C_ 1$$ است و در اینجا از بیان آن صرف‌نظر می‌کنیم.

اثبات بخش (ب) مشابه (الف)‌ است. باید علامت نمایی را بررسی کنیم و مطمئن شویم که مثبت است.

محاسبه انتگرال‌های $$\LARGE \int _ { -\infty } ^ \infty$$ و $$\LARGE \int _ 0 ^ \infty$$

این بخش را با چند مثال بررسی می‌کنیم و از قضایای بخش قبل استفاده خواهیم کرد.

مثال ۱

حاصل انتگرال زیر را به دست آورید.

$$\large \int _ {-\infty} ^ \infty \frac { 1 } { ( 1 + x ^ 2 ) ^ 2 } d x .$$

حل: تابع زیر را در نظر بگیرید:

$$\large f ( z ) = 1 / ( 1 + z ^ 2 ) ^ 2 .$$

برای $$z$$های بزرگ، داریم:‌

$$\large f ( z ) \approx 1 / z ^ 4 .$$

عملاً فرض قضیه ۱ برقرار است. با استفاده از کانتور شکل زیر، طبق قضیه مانده، داریم:

(باقیمانده‌های $$f$$ درون کانتور) $$\large \int _ { C _ { 1 } + C _ { n } } f ( z ) d z = 2 \pi i \sum$$

هر یک از تکه‌های معادله بالا را بررسی می‌کنیم.

• $$\int _ { C _ R} f ( z ) d z$$ (طبق قضیه ۱ (الف)):

$$\large \lim _ {R \to \infty} \int _ { C_ R} f ( z ) d z = 0 .$$

• $$\int _ { C _ 1 } f ( z ) d z$$:

$$\large \lim _ { R \rightarrow \infty } \int _ { C _ { 1 } } f ( z ) d z = \lim _ { R \rightarrow \infty } \int _ { - R } ^ { R } f ( x ) d x = \int _ { - \infty } ^ { \infty } f ( x ) d x = I$$

در نهایت، باقیمانده‌های مورد نیاز را محاسبه می‌کنیم: $$f ( z )$$ در $$\pm i$$ قطب‌های مرتبه ۲ دارد. فقط $$z = i$$ درون کانتور است، بنابراین، باقیمانده در آن را حساب می‌کنیم. تابع زیر را در نظر بگیرید:‌

$$\large g ( z ) = ( z - i ) ^ { 2 } f ( z ) = \frac { 1 } { ( z + i ) ^ { 2 } }$$

بنابراین:

$$\large \operatorname {Res} ( f , i ) = g ^ { \prime } ( i ) = -\frac { 2 } { ( 2 i ) ^ { 3 } } = \frac { 1 } { 4 i }$$

در نتیجه، خواهیم داشت:

$$\large I = 2 \pi i \operatorname {Res} ( f , i ) = \frac { \pi } { 2 }$$

مثال ۲

انتگرال زیر را محاسبه کنید.

$$\large I = \int _ { - \infty } ^ { \infty } \frac { 1 } { x ^ { 4 } +1 } d x$$

حل: تابع $$f ( z ) = 1 / ( 1 + z ^ 4 )$$ را در نظر بگیرید. از کانتور مشابه مثال قبل استفاده می‌کنیم.

مشابه مثال قبل، داریم:

$$\large \lim _ { R \rightarrow \infty } \int _ { C _ { R } } f ( z ) d z = 0$$

و

$$\large \lim _ { R \rightarrow \infty } \int _ { C _ { 1 } } f ( z ) d z = \int _ { - \infty } ^ { \infty } f ( x ) d x = I$$

بنابراین، طبق قضیه باقیمانده، داریم:

(باقیمانده $$f$$ درون کانتور) $$I = \lim _ { R \rightarrow \infty } \int _ { C _ { 1 } + C _ { R } } f ( z ) d z = 2 \pi i \sum$$

همه قطب‌های $$f$$ ساده هستند:

$$\large e ^ { i \pi / 4 } , e ^ { i 3 \pi / 4 } , e ^ { i 5 \pi / 4} , e ^ { i 7 \pi / 4 } .$$

فقط $$e ^ { i \pi / 4 }$$ و $$e ^ { i 3 \pi / 4 }$$ درون کانتور قرار دارند. باقیمانده آن‌ها را با استفاده از قاعده هوپیتال محاسبه می‌کنیم. برای $$z _ 1 = e ^ { i \pi / 4 }$$، داریم:‌

$$\large \operatorname {Res} \left ( f , z _ { 1 } \right ) = \lim _ { z \rightarrow z _ { 1 } } \left ( z - z _ { 1 } \right ) f ( z ) = \lim _ { z \rightarrow z _ { 1 } } \frac { z - z _ { 1 } } { 1 + z ^ { 4 } } = \lim _ { z \rightarrow z _ { 1 } } \frac { 1 } { 4 z ^ { 3 } } = \frac { 1 } { 4 \mathrm { e } ^ { i 3 \pi / 4 } } = \frac { \mathrm { e } ^ { - i 3 \pi / 4 } } { 4 }$$

و برای $$z _ 2 = e ^ { i 3 \pi / 4 }$$، خواهیم داشت:

$$\large \operatorname {Res} \left ( f , z _ { 2 } \right ) = \lim _ { z \rightarrow z _ { 2 } } \left ( z - z _ { 2 } \right ) f ( z ) = \lim _ { z \rightarrow z _ { 2 } } \frac { z - z _ { 2 } } { 1 + z ^ { 4 } } = \lim _ { z \rightarrow z _ { 2 } } \frac { 1 } { 4 z ^ { 3 } } = \frac { 1 } { 4 \mathrm {e} ^ { i 9 \pi / 4 } } = \frac { \mathrm { e } ^ { - i \pi / 4 } } { 4 }$$

بنابراین:

$$\large I = 2 \pi i \left ( \operatorname {Res} \left ( f , z _ { 1 } \right ) + \operatorname {Res} \left ( f , z _ { 2 } \right ) \right ) = 2 \pi i \left ( \frac { - 1 - i } { 4 \sqrt { 2 } } + \frac { 1 - i } { 4 \sqrt { 2 } } \right ) = 2 \pi i \left ( - \frac { 2 i } { 4 \sqrt { 2 } } \right ) = \pi { \frac { \sqrt { 2 } } { 2 } }$$

مثال ۳

با فرض $$b > 0$$، تساوی زیر را اثبات کنید:

$$\large \int _ { 0 } ^ { \infty } \frac { \cos ( x ) }{ x ^ { 2 } + b ^ { 2 } } d x = \frac { \pi \mathrm { e } ^ { - b } } { 2 b }$$

حل: انتگرالده زوج است، بنابراین، خواهیم داشت:

$$\large I = \frac { 1 } { 2 } \int _ { - \infty } ^ { \infty } \frac { \cos ( x ) } { x ^ { 2 } + b ^ { 2 } }$$

همچنین، با توجه به توان ۲ در مخرج آن، می‌توان گفت که انتگرال کاملاً همگرا است.

باید توجه کنیم از آنجا که $$\cos ( z )$$ در هر دو نیم‌صفحه به بینهایت می‌رود، مفروضات قضیه ۱ برقرار نیستند. برای رفع این مشکل $$\cos ( x )$$ را با $$e ^ { i x }$$ جایگزین می‌کنیم. بنابراین، خواهیم داشت:

$$\large \tilde { I } = \int _ { - \infty } ^ { \infty } \frac { \mathrm { e } ^ { i x } } { x ^ { 2 } + b ^ { 2 } } d x , \quad \text { } \quad I = \frac { 1 } { 2 } \operatorname {Re} ( \tilde { I } )$$

حال تابع زیر را در نظر بگیرید:‌

$$\large f ( z ) = \frac { \mathrm { e } ^ { i z } } { z ^ { 2 } + b ^ { 2 } }$$

برای $$z = x + i y$$ و $$y > 0$$، داریم:

$$\large | f ( z ) | = \frac { \left | \mathrm { e } ^ { i ( x + i y ) } \right | } { \left | z ^ { 2 } + b ^ { 2 } \right | } = \frac { \mathrm { e } ^ { - y } } { \left | z ^ { 2 } + b ^ { 2 } \right | }$$

از آنجا که $$e ^ { - y } < 1$$ است، $$f ( z )$$ در مفروضات قضیه ۱ در نیم‌صفحه بالایی صدق می‌کند. اکنون می‌توانیم از کانتور مشابه مثال‌های قبل استفاده کنیم.

داریم:

$$\large \lim _ { R \rightarrow \infty } \int _ { C _ { R } } f ( z ) d z = 0$$

و

$$\large \lim _ { R \rightarrow \infty } \int _ { C _ { 1 } } f ( z ) d z = \int _ { - \infty } ^ { \infty } f ( x ) d x = \tilde { I }$$

(باقیمانده‌های $$f$$ درون کانتور) $$\tilde { I } = \lim _ { R \rightarrow \infty } \int _ { C _ { 1 } + C _ { R } } f ( z ) d z = 2 \pi i \sum$$

قطب‌های $$f$$ در $$a \pm bi$$ قرار دارند و هر دو ساده هستند. فقط $$b i$$ درون کانتور قرار دارد. باقیمانده را با استفاده از قاعده هوپیتال محاسبه می‌کنیم:

$$\large \operatorname {Res} ( f , b i ) = \lim _ { z \rightarrow b i } ( z - b i ) \frac { \mathrm { e } ^ { i z } } { z ^ { 2 } + b ^ { 2 } } = \frac { \mathrm { e } ^ { - b } } { 2 b i }$$

بنابراین، داریم:

$$\large \tilde { I } = 2 \pi i \operatorname {Res} ( f , b i ) = \frac { \pi \mathrm { e } ^ { - b } } { b }$$

و در نهایت خواهیم داشت:

$$\large I = \frac { 1 } { 2 } \operatorname {Re} ( \tilde { I } ) = \frac { \pi \mathrm { e } ^ { - b } } { 2 b }$$

محاسبه انتگرال‌های مثلثاتی

برای محاسبه این انتگرال‌ها از برخی ویژگی‌های ابتدایی $$z = e ^ { i \theta}$$ روی دایره واحد استفاده می‌کنیم:

۱) $$\mathrm { e } ^ { - i \theta } = 1 / z$$

۲) $$\cos ( \theta ) = \frac { \mathrm { e } ^ { i \theta } + \mathrm { e } ^ { - i \theta } } { 2 } = \frac { z + 1 / z } { 2 }$$

۳) $$\sin ( \theta ) = \frac { \mathrm { e } ^ { i \theta } - \mathrm { e } ^ { - i \theta } } { 2 i } = \frac { z - 1 / z } { 2 i }$$

مثال ۴

با فرض $$|a| \neq 1$$، انتگرال زیر را محاسبه کنید:

$$\large \int _ { 0 } ^ { 2 \pi } \frac { d \theta } { 1 + a ^ { 2 } - 2 a \cos ( \theta ) } .$$

حل: پارامتری کردن دایره واحد به صورت $$z = e ^ { i \theta }$$ در بازه $$[ 0 , 2 \pi ]$$ است. از تغییر متغیر زیر استفاده می‌کنیم:

$$\large \begin {aligned} \cos ( \theta ) & = \frac { z + 1 / z } { 2 } \\ d z & = i \mathrm { e } ^ { i \theta } d \theta \quad \Leftrightarrow \quad d \theta = \frac { d z } { i z } \end {aligned}$$

با این تغییر متغیرها، خواهیم داشت:‌

$$\large \begin {aligned} I & = \int _ { 0 } ^ { 2 \pi } \frac { d \theta } { 1 + a ^ { 2 } - 2 a \cos ( \theta ) } \\ & = \int _ { | z | = 1 } \frac { 1 } { 1 + a ^ { 2} - 2 a ( z + 1 / z ) / 2 } \cdot \frac { d z } { i z } \\ & = \int _ { | z | = 1 } \frac { 1 } { i \left ( \left ( 1 + a ^ { 2 } \right ) z - a \left (z ^ { 2 } + 1 \right ) \right ) } d z \end {aligned}$$

بنابراین، داریم:

$$\large f ( z ) = \frac { 1 } { i \left ( \left ( 1 + a ^ { 2 } \right ) z - a \left ( z ^ { 2 } + 1 \right ) \right ) }$$

طبق قضیه مانده، رابطه زیر برقرار است:

(باقیمانده‌های $$f$$ درون دایره واحد) $$I = 2 \pi i \sum$$

می‌توانیم از مخرج فاکتورگیری کنیم:

$$\large f ( z ) = \frac { - 1 } { i a ( z - a ) ( z - 1 / a ) }$$

همان‌گونه که می‌بینیم، قطب‌ها در $$a$$ و $$1 / a$$ قرار دارند که یکی از آن‌ها درون دایره واحد است و دیگری در خارج از آن:

• اگر $$| a | > 1$$ باشد، آنگاه $$1 / a$$ درون دایره واحد بوده و $$\mathrm{Res}(f , 1/ a ) = \frac {1 } { i (a^2-1)}$$.
• اگر $$| a | < 1$$ باشد، آنگاه $$a$$ درون دایره واحد بوده و $$\mathrm{Res}(f , a ) = \frac {1 } { i (1-a^2)}$$.

بنابراین، داریم:

$$\large I = \left \{ \begin {array} { l l } \frac { 2 \pi } { a ^ { 2 } - 1 } , & \text { } | a | > 1 \\ \frac { 2 \pi } { 1 - a ^{ 2 } } , & \text { } | a | < 1 \end {array} \right .$$

قضیه ۳: فرض کنید $$R ( x , y)$$ یک تابع گویا و بدون قطب روی دایره زیر باشد:

$$\large x ^ 2 + y ^ 2 = 1$$

در نتیجه، برای

$$\large f ( z ) = \frac { 1 } { i z } R \left ( \frac { z + 1 / z } { 2 } , \frac { z - 1 / z } { 2 i } \right )$$

خواهیم داشت:

(باقیمانده‌های $$f$$ درون $$|z|=1$$) $$\int _ { 0 } ^ { 2 \pi } R ( \cos ( \theta ) , \sin ( \theta ) ) d \theta = 2 \pi i \sum$$

اثبات: از تغییر متغیرهایی مشابه مثال قبل استفاده می‌کنیم. بنابراین، خواهیم داشت:

$$\large \int _ { 0 } ^ { 2 \pi } R ( \cos ( \theta ) , \sin ( \theta ) ) d \theta = \int _ { | z | = 1 } R \left ( \frac { z + 1 / z } { 2 } , \frac { z - 1 / z } { 2 i } \right ) \frac { d z } { i z }$$

فرض درباره قطب‌ها بدین معنی است که $$f$$ قطبی روی کانتور $$| z | = 1$$ ندارد. بنابراین، قضیه باقیمانده این قضیه را اثبات می‌کند.

محاسبه انتگرال با برش شاخه‌ای انتگرالده

این بخش را نیز با مثال بررسی می‌کنیم.

مثال ۵

انتگرال زیر را محاسبه کنید:

$$\large I = \int _ 0 ^ \infty \frac { x ^ {1/3}} { 1 + x ^ 2 } d x .$$

حل: تابع زیر را در نظر می‌گیریم:

$$\large f ( x ) = \frac { x ^ {1/3}} { 1 + x ^ 2 } .$$

از آنجا که تابع بالا به صورت مجانبی با $$x ^ { - 5 / 3 }$$ قابل مقایسه است، انتگرال کاملاً همگرا است. به عنوان تابع مختلطِ

$$\large f ( z ) = \frac { z ^ {1/3}} { 1 + z ^ 2 } .$$

به یک بریدگی شاخه برای تحلیلی (یا حتی پیوسته)‌ بودن نیاز داریم، بنابراین، نیاز خواهیم داشت آن را همراه با انتخاب کانتور در نظر بگیریم.

ابتدا بریدگی شاخه زیر را در طول محور حقیقی مثبت انتخاب می‌کنیم. برای $$z = r e ^ { i \theta}$$ روی بریدگی محور نیست و داریم $$0 < \theta < 2 \pi$$.

در ادامه، از کانتور $$C_ 1 + C_ R - C_ 2 - C_ r$$ شکل زیر استفاده می‌کنیم.

$$r$$ و شعاع دایره خارجی $$R$$ است)." width="273" height="214">

علامت تکه‌ها را به‌ گونه‌ای قرار می‌دهیم که انتگرال‌ها به صورت طبیعی پارامتری شوند. از آنجا که $$C_ 1$$ و $$C_ 2$$ بریدگی شاخه مخالف هم دارند، داریم:

$$\large \int _ { C_ 1 - C _ 2 } f ( z ) d z \neq 0 .$$

ابتدا انتگرال را روی هر تکه از منحنی بررسی می‌کنیم.

• روی $$C_ R$$: طبق قضیه ۱، داریم:

$$\large \lim _ { R \to \infty } \int _ { C _ R} f ( z ) d z = 0 .$$

• روی $$C_ r$$:‌ برای درک بهتر، فرض می‌کنیم $$r < 1 / 2$$. رابطه $$| z | = r$$ را داریم، بنابراین:

$$\large | f ( z ) | = \frac { \left | z ^ { 1 / 3 } \right | } { \left | 1 + z ^ { 2 } \right | } \leq \frac { r ^ { 1 / 3 } } { 1 - r ^ { 2 } } \leq \frac { ( 1 / 2 ) ^ { 1 / 3 } } { 3 / 4 }$$

عدد آخر در معادله بالا را $$M$$ می‌نامیم. نشان دادیم که برای $$r$$ کوچک، $$| f ( z ) | < M$$ است. بنابراین:

$$\large \left | \int _ { C _ { r } } f ( z ) d z \right | \leq \int _ { 0 } ^ { 2 \pi } \left | f \left ( r e ^ { i \theta } \right ) \| i r e ^ { i \theta } \right | d \theta \leq \int _ { 0 } ^ { 2 \pi } M r d \theta = 2 \pi M r$$

واضح است که وقتی $$r \to 0$$، عبارت بالا به صفر میل می‌کند.

• روی $$C_ 1$$:

$$\large \lim _ { r \rightarrow 0 , R \rightarrow \infty } \int _ { C _ { 1 } } f ( z ) d z = \int _ { 0 } ^ { \infty } f ( x ) d x = I$$

• روی $$C_ 2$$: اساساً داریم: $$\theta = 2 \pi$$، بنابراین، $$z ^ { 1 / 3 } = e ^ {i 2 \pi / 3} | z | ^ { 1 / 3 }$$. در نتیجه:

$$\large \lim _ { r \rightarrow 0 , R \rightarrow \infty } \int _ { C _ { 2 } } f ( z ) d z = \mathrm { e } ^ { i 2 \pi / 3 } \int _ { 0 } ^ { \infty } f ( x ) d x = \mathrm { e } ^ { i 2 \pi / 3 } I.$$

قطب‌های $$f ( z )$$ در $$\pm i$$ قرار دارند. از آنجا که $$f$$ درون کانتور «برخه‌ریخت» (Meromorphic) است، طبق قضیه مانده داریم:

$$\large \int _ { C _ { 1 } + C _ { R } - C _ { 2 } - C _ { r } } f ( z ) d z = 2 \pi i ( \operatorname {Res} ( f , i ) + \operatorname {Res} ( f , - i ) )$$

با $$r \to 0$$ و $$R \to \infty$$، تحلیل بالا نشان می‌دهد:

$$\large \left ( 1 - \mathrm {e} ^ { i 2 \pi / 3 }\right ) I = 2 \pi i ( \operatorname {Res} ( f , i ) + \operatorname {Res} ( f , - i ) )$$

باقیمانده‌ها به صورت زیر هستند:

$$\large \begin {aligned} \operatorname {Res} ( f , - i ) & = \frac { ( - i ) ^ { 1 / 3 } } { - 2 i } = \frac { \left ( \mathrm { e } ^ { i 3 \pi / 2 } \right ) ^ { 1 / 3 } } { 2 \mathrm { e } ^ { i 3 \pi / 2 } } = \frac { \mathrm { e } ^ { - i \pi } } { 2 } = - \frac { 1 } { 2 } \\ \operatorname {Res} ( f , i ) & = \frac { i ^ { 1 / 3 } } { 2 i } = \frac { \mathrm { e } ^ { i \pi / 6 } } { 2 \mathrm { e } ^ { i \pi / 2 } } = \frac { \mathrm { e } ^ { - i \pi / 3 } } { 2 } \end {aligned}$$

با کمی عملیات جبری، داریم:

$$\large \left ( 1 - \mathrm { e } ^ { i 2 \pi / 3 } \right ) I = 2 \pi i \cdot \frac { - 1 + \mathrm { e } ^ { - i \pi / 3 } } { 2 } = \pi i ( - 1 + 1 / 2 - i \sqrt { 3 } / 2 ) = - \pi i \mathrm { e } ^ { i \pi / 3 }$$

و در نتیجه:

$$\large I = \frac { - \pi i \mathrm { e } ^ { i \pi / 3 } } { 1 - \mathrm { e } ^ { i 2 \pi / 3 } } = \frac { \pi i }{ \mathrm { e } ^ { i \pi / 3 } - \mathrm { e } ^ { - \pi i / 3 } } = \frac { \pi / 2 } { \left ( \mathrm { e } ^ { i \pi / 3 } - \mathrm { e } ^ { - i \pi / 3 } \right ) / 2 i } = \frac { \pi / 2 } { \sin ( \pi / 3 ) } = \frac { \pi } { \sqrt { 3 } }$$

مثال ۶

انتگرال زیر را محاسبه کنید.

$$\large I = \int _ { 1 } ^ { \infty } \frac { d x } { x \sqrt { x ^ { 2 } - 1 } }$$

حل: تابع زیر را در نظر می‌گیریم:

$$\large f ( z ) = \frac { 1 } { z \sqrt { z ^ { 2 } - 1 } }$$

اولین چیزی که باید نشان دهیم، این است که انتگرالِ

$$\large \int _ { 1 } ^ { \infty } f ( x ) d x$$

کاملاً همگرا است. برای انجام این کار، انتگرال را به دو بخش تبدیل می‌کنیم:

$$\large \int _ { 1 } ^ { \infty } \frac { d x } { x \sqrt { x ^ { 2 } - 1 } } = \int _ { 1 } ^ { 2 } \frac { d x } { x \sqrt { x ^ { 2 } - 1 } } + \int _ { 2 } ^ { \infty } \frac { d x } { x \sqrt { x ^ { 2 } - 1 } }$$

انتگرال اول سمت راست را می‌توان به صورت زیر نوشت:

$$\large \int _ { 1 } ^ { 2 } \frac { 1 } { x \sqrt { x + 1 } } \cdot \frac { 1 } { \sqrt { x - 1 } } d x \leq \int _ { 1 } ^ { 2 } \frac { 1 } { \sqrt { 2 } } \cdot \frac { 1 } { \sqrt { x - 1 } } d x = \left . \frac { 2 } { \sqrt { 2 } } \sqrt { x - 1 } \right | _ { 1 } ^ { 2 }$$

این نشان می‌دهد که انتگرال اول همگرای مطلق است.

تابع $$f ( x )$$ به صورت مجانبی قابل مقایسه با $$1 / x ^ 2$$ است، بنابراین، انتگرال از $$2$$ تا $$\infty$$ نیز کاملاً همگرا است.

اکنون می‌توانیم نتیجه بگیریم که انتگرال اصلی مطلقاً همگرا است.

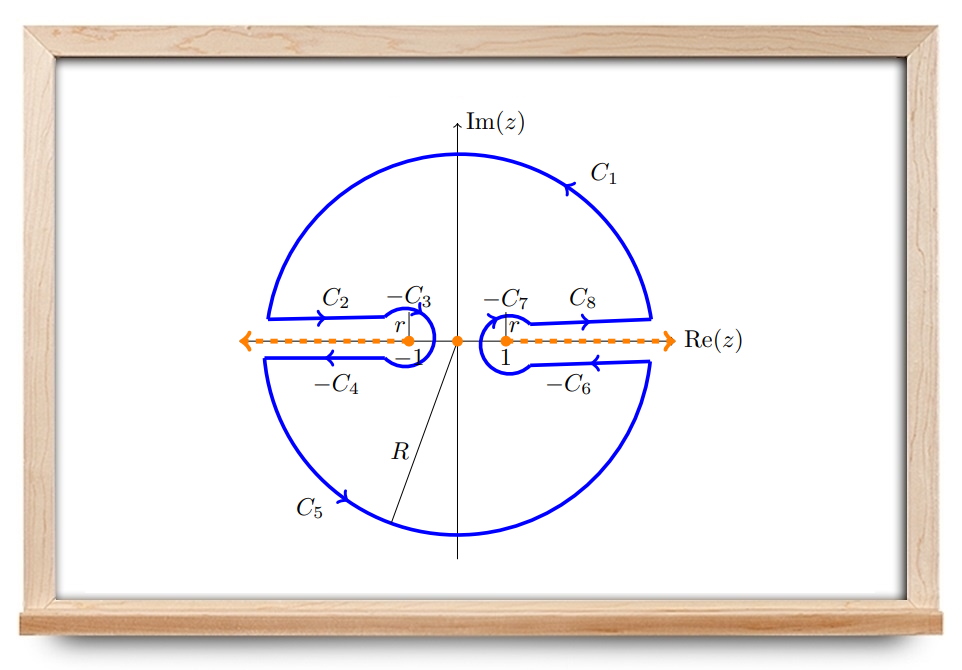
در ادامه، از کانتور زیر استفاده می‌کنیم. فرض می‌کنیم دایره‌های بزرگ دارای شعاع $$R$$ هستند و شعاع دایره‌های کوچک $$r$$ است.

از بریدگی شاخه برای ریشه دوم استفاده می‌کنیم که محور حقیقی مثبت را حذف می‌کند. در این شاخه، داریم:

$$0 < \mathrm {arg} ( z ) < 2 \pi$$ و $$0 < \mathrm {arg} ( \sqrt {w}) < \pi$$

برای $$f ( z )$$، این مورد بریدگی شاخه را الزام می‌کند که پرتوهای $$[ 1 , \infty )$$ و $$( - \infty , - 1 ]$$ را از صفحه مختلط حذف کند.

قطب در $$z = 0$$ تنها تکینگی $$f ( z )$$ درون کانتور است. به سادگی می‌توان محاسبه کرد:

$$\large \operatorname {Res} ( f , 0 ) = \frac { 1 }{ \sqrt { - 1 } } = \frac { 1 } { i } = - i$$

بنابراین، طبق قضیه مانده، داریم:

$$\large \int _ { C _ { 1 } + C _ { 2 } - C _ { 3 } -C _ { 4 } + C _ { 3 } - C _ { 6 } - C _ { 7 } + C _ { 3 } } f ( z ) d z = 2 \pi i \operatorname {Res} ( f , 0 ) = 2 \pi$$

حدهای زیر را داریم (آن‌ها را اثبات می‌کنیم):

$$\large \begin {array} { l } \lim _ { R \rightarrow \infty } \int _ { C _ { 1 } } f ( z ) d z = \lim _ { R \rightarrow \infty } \int _ { C _ { 3 } } f ( z ) d z = 0 \\ \lim _ { r \rightarrow 0 } \int _ { C _ { 3 } } f ( z ) d z = \lim _ { r \rightarrow 0 } \int _ { C _ { 7 } } f ( z ) d z = 0 \end {array}$$

همچنین می‌توان نشان داد:

$$\large \begin {aligned} \lim _ { R \rightarrow \infty , r \rightarrow 0 } \int _ { C _ { 2 } } f ( z ) d z & = \lim _ { R \rightarrow \infty , r \rightarrow 0 } \int _ { - C _ { 4 } } f ( z ) d z \\ & = \lim _ { R \rightarrow \infty , r \rightarrow 0 } \int _ { -\infty } f ( z ) d z = \lim _ { R \rightarrow \infty , r \rightarrow 0 } \int _ { C _ { 0 } } f ( z ) d z = I \end {aligned}$$

با استفاده از این حدود، تساوی $$4 I = 2 \pi$$ را خواهیم داشت، یعنی:

$$\large I = \pi / 2$$

حدها برای $$C_ 1$$ و $$C_ 5$$ از قضیه ۱ تبعیت می‌کنند، زیرا برای $$z$$های بزرگ:

$$\large | f ( z ) | \approx 1 / | z | ^ { 3 / 2 }$$

حد را برای $$C_ 3$$ به صورت زیر محاسبه می‌کنیم. فرض کنید $$r$$ کوچک (بسیار کوچک‌تر از $$1$$) باشد. اگر $$z = - 1 + r e ^ { i \theta }$$ روی $$C_ 3$$ باشد، آنگاه:

$$\large | f ( z ) | = \frac { 1 } { | z \sqrt { z - 1 } \sqrt { z + 1 } | } = \frac { 1 } { \left | - 1 + r \mathrm { e } ^ { i \theta } \right | \sqrt { \left | - 2 + r \mathrm { e } ^ { i \theta } \right | \sqrt { r } } } \leq \frac { M } { \sqrt { r } }$$

که در آن، $$M$$ به گونه‌ای انتخاب شده که بزرگ‌تر از عبارت زیر باشد:

$$\large \frac { 1 } { \left | - 1 + r e ^ { i \theta } \right | \sqrt { \left | - 2 + r e ^ { i \theta } \right | } }$$

بنابراین:

$$\large \left | \int _ { C _ { 3 } } f ( z ) d z \right | \leq \int _ { C _ { 3 } } \frac { M } { \sqrt { r } } | d z | \leq \frac { M } { \sqrt { r } } \cdot 2 \pi r = 2 \pi M \sqrt { r }$$

واضح است که وقتی $$r \to 0$$، عبارت آخر به صفرمیل می‌کند. حد انتگرال روی $$C_ 7$$ به طور مشابه به دست می‌آید.

خط راست $$C _ 8$$ را می‌توانیم به صورت زیر پارامتری کنیم:

$$\large z = x + i \epsilon$$

که در آن، $$\epsilon$$ یک عدد مثبت کوچک است و $$x$$ از (تقریباً) ۱ تا $$\infty$$ تغییر می‌کند. بنابراین، روی $$C_ 8$$، داریم:

$$\mathrm{arg} ( z ^ 2 - 1 ) \approx 0$$ و $$f ( z ) \approx f ( x )$$.

همه این تقریب‌ها با $$r \to 0$$ دقیق می‌شوند. بنابراین، داریم:

$$\large \lim _ { R \rightarrow \infty , r \rightarrow 0 } \int _ { C _ { 8 } } f ( z ) d z = \int _ { 1 } ^ { \infty } f ( x ) d x = I$$

$$- C_ 6$$ را به صورت زیر پارامتری می‌کنیم:

$$z = x - i \epsilon$$

که در آن، $$\epsilon$$ یک عدد مثبت کوچک است و $$x$$ از $$\infty$$ تا ۱ تغییر می‌کند. بنابراین، می‌توان نوشت:

$$\large \arg \left ( z ^ { 2 } - 1 \right ) \approx 2 \pi$$

در نتیجه:

$$\large \sqrt { z ^ { 2 } - 1 } \approx - \sqrt { x ^ { 2 } - 1 }$$

و بنابراین:

$$\large f ( z ) \approx - \frac { 1 } { x \sqrt { x ^ { 2 } - 1 } } = - f ( x )$$

در نتیجه، خواهیم داشت:

$$\large \lim _ { R \rightarrow \infty , r \rightarrow 0 } \int _ { -C _ { 6 } } f ( z ) d z = \int _ { \infty } ^ { 1 } - f ( x ) d x = \int _ { 1 } ^ { \infty } f ( x ) d x = I$$

می‌توانیم $$C _ 2$$ را با $$z = - x + i \epsilon$$ پارامتری کنیم که در آن، $$x$$ از $$\infty$$ به $$1$$ می‌رود. بنابراین، روی $$C_ 2$$، داریم:

$$\large \arg \left ( z ^ { 2 } - 1 \right ) \approx 2 \pi$$

این نشان می‌دهد:

$$\large \sqrt { z ^ { 2 } - 1 } \approx - \sqrt { x ^ { 2 } - 1 }$$

در نتیجه:

$$\large f ( z ) \approx \frac { 1 } { (- x ) ( - \sqrt{x ^ 2 - 1 } )}= f ( x ) .$$

و در نهایت، خواهیم داشت:

$$\large \lim _ { R \rightarrow \infty , r \rightarrow 0 } \int _ { C _ { 2 } } f ( z ) d z = \int _ { \infty } ^ { 1 } f ( x ) ( - d x ) = \int _ { 1 } ^ { \infty } f ( x ) d x = I$$

اگر این مطلب برای شما مفید بوده است، آموزش‌ها و مطالب زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس ریاضیات
• آموزش ریاضیات مهندسی
• مجموعه آموزش‌های ریاضیات و فیزیک پایه
• آموزش ریاضیات مهندسی (مرور – تست کنکور ارشد)
• فراکتال چیست؟ — به زبان ساده
• توان و ریشه اعداد مختلط — از صفر تا صد
• فرم نمایی و قطبی اعداد مختلط — به زبان ساده

^^