تحلیل ضریب همبستگی اسپیرمن در SPSS — از صفر تا صد

در آمار، برای نمایش میزان وابستگی بین دو یا چند متغیر، از شاخص‌های مختلفی استفاده می‌شود. یکی از معمول‌ترین این شاخص‌ها، ضرایب همبستگی است که میزان وابستگی را به صورت استاندارد شده نمایش می‌دهند. معمولا ضرایب همبستگی مقداری در بازه ۱- تا ۱ دارند. هر چه مقدار قدرمطلق این ضریب‌ها به یک نزدیک‌تر باشد، میزان وابستگی بین متغیرها بیشتر است. در این بین ضریب همبستگی اسپیرمن به علت ساختار مطلوبی که برای داده‌های رتبه‌‌ای دارد، در مباحث روانشناسی، مدیریت و آمار به کار گرفته می‌شود. در این نوشتار از مجله فرادرس به نحوه محاسبه، کاربرد و تحلیل ضریب همبستگی اسپیرمن در SPSS خواهیم پرداخت. واضح است که از نرم‌افزار SPSS برای بدست آوردن ضریب همبستگی و آزمون‌ها معنی‌داری آن استفاده خواهیم کرد.

برای آشنایی بیشتر با ضریب‌های همبستگی و کاربرد آن‌ها، پیشنهاد می‌شود، مطلب دیگر مجله فرادرس با عنوان ضریب همبستگی (Correlation Coefficients) و شیوه‌ محاسبه آن‌ها — به زبان ساده و امید ریاضی (Mathematical Expectation) — مفاهیم و کاربردها را مطالعه کنید. همچنین خواندن نوشتارهای کوواریانس و نحوه محاسبه آن — به زبان ساده و ضریب همبستگی و ماتریس همبستگی در R — کاربرد در یادگیری ماشین نیز خالی از لطف نیست.

تحلیل ضریب همبستگی اسپیرمن در SPSS

ضریب همبستگی اسپیرمن یا به طور دقیق «ضریب همبستگی رتبه‌ای اسپیرمن» (Spearman rank-order correlation coefficient) اندازه یا شاخصی غیرپارامتری، جهت نمایش وابستگی بین دو متغیر ترتیبی است. البته از ضریب همبستگی اسپیرمن برای متغیرها کمی (عددی) نیز می‌توان استفاده کرد. معمولا برای نمایش ضریب همبستگی اسپیرمن از نماد $$r_s$$ یا $$\rho$$ (تلفظ کنید «رو») استفاده می‌شود.

فیلم آموزش همبستگی و رگرسیون خطی در اس پی اس اس SPSS در فرادرس

کلیک کنید

شاخص همبستگی اسپیرمن به افتخار «چارلز اسپیرمن» (Charles Spearman) دانشمند روانشناس انگلیسی، نام‌گذاری شده است. او با استفاده از این ضریب همبستگی توانست نظریه‌هایش در حوزه شناخت و هوش را توسعه دهد.

ضریب همبستگی اسپیرمن برای متغیرهای ترتیبی یا برای داده‌های پیوسته قابل محاسبه است. البته اغلب زمانی از این ضریب همبستگی استفاده می‌شود که شرایط و فرضیه‌های لازم برای محاسبه «ضریب همبستگی پیرسون» (Peasron Correlation Coefficient) وجود نداشته باشد. به عنوان مثال، شما می‌توانید از ضریب همبستگی اسپیرمن برای درک اینکه آیا ارتباطی بین نمره آزمون و زمان صرف شده برای مطالعه وجود دارد، استفاده کنید. یا در مورد ارتباطی بین افسردگی و طول دوره بیکاری تحقیق کنید.

نکته: شاخص‌های وابستگی بین دو متغیر توسط اندازه‌های «ضریب همبستگی پیرسون»، «ضریب همبستگی رتبه‌ای اسپیرمن» یا «ضریب هماهنگی تاو کندال» (Kendall's Tau) محاسبه می‌شوند.

شرایط و فرضیه‌های برای تحلیل ضریب همبستگی اسپیرمن

قبل از آنکه تحلیل ضریب همبستگی اسپیرمن را برای داده‌ها مورد استفاده قرار دهید، باید شرایط به کارگیری این تحلیل را بررسی کنید. در ادامه متن به فرض‌ها و شرایطی اشاره خواهیم کرد که داده‌ها برای تحلیل ضریب همبستگی اسپیرمن باید داشته باشند. البته به کمک نرم‌افزار SPSS نیز وجود این شرایط را تحقیق خواهیم کرد.

فرض شماره 1: دو متغیر شما باید بوسیله یکی از مقیاس‌های «ترتیبی» (Ordinal)، «فاصله» (Interval) یا «نسبتی» (Ratio) اندازه‌گیری شده باشند. به عنوان نمونه می‌توان متغیرهای ترتیبی که از طریق مقیاس‌های لیکرت (به عنوان مثال، مقیاس 7 مقداری لیکرت از «کاملاً موافق» تا «کاملاً مخالف») بدست آمده‌اند را در تحلیل ضریب همبستگی اسپیرمن به کار برد.

داده‌های دیگر که براساس مقیاس ترتیبی یا رتبه‌ای اندازه‌گیری می‌شوند شامل مواردی مانند، زمان مطالعه (برحسب ساعت)، ضریب هوش (برحسب نمره ضریب هوشی IQ) و نمره آزمون (امتیاز از 0 تا 100) هستند.

فرض شماره 2: داده‌هایی که برای تحلیل ضریب همبستگی  اسپیرمن به کار می‌برید باید به صورت زوج-مشاهده باشند. به عنوان مثال، تصور کنید که به رابطه بین مصرف روزانه سیگار و میزان زمان ورزش افراد در هر هفته علاقمندید. یک مشاهده زوجی در این حالت، نمره هر متغیر را برای هر فرد منعکس می‌کند. در این صورت زوجی به شکل (تعداد مصرف سیگار روزانه ، میزان ساعت ورزش انجام شده هر هفته توسط) خواهیم داشت. اگر فرض کنید که ۳۰ شرکت کننده در این طرح نمونه‌گیری شده‌اند، باید ۳۰ زوج مرتب و ۶۰ داده داشته باشید.

فرض شماره 3: فرض بر این است که دو متغیر (مولفه اول با مولفه دوم زوج مرتب) دارای رابطه یا همبستگی هستند. به این ترتیب با محاسبه ضریب همبستگی اسپیرمن، شدت این رابطه سنجیده می‌شود. همانطور که گفتیم، مقادیر نزدیک به ۱، نشانگر شدت رابطه مستقیم و مقادیر نزدیک به ۱- رابطه معکوس را نشان می‌دهند. در حالتی که رابطه مستقیم است، جهت تغییرات دو متغیر در یک راستا است. ولی در حالتی که رابطه معکوس باشد، جهت تغییرات متغیرها عکس یکدیگر خواهد بود. معمولا برای نمایش یا ارزیابی وجود رابطه بین دو  متغیر از نمودار پراکندگی (scatterplot) استفاده می‌شود. ما هم در این متن در اولین اقدام، با رسم چنین نموداری، رابطه بین متغیرها را بررسی کرده، سپس به محاسبه شدت رابطه خواهیم پرداخت. در تصویر ۲، نمونه‌ای از انواع رابطه بین متغیرهای زوجی را مشاهده می‌کنید.

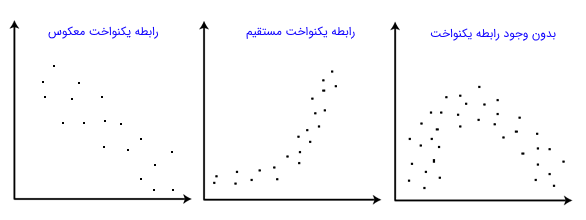
همانطور که در تصویر ۲ مشاهده می‌کنید، در تصویر سمت راست، هیچ رابطه «یکنواختی» (Monotonic) بین مقادیر محور افقی و عمودی دیده نمی‌شود. از طرفی در نمودار میانی، یک رابطه یکنواخت مستقیم (غیرخطی) را مشاهده می‌کنید. در نمودار سمت چپ نیز یک رابطه خطی معکوس مشاهده می‌شود.

در صورتی که رابطه بین دو متغیر یکنواخت (Monotone) باشد، می‌توان شدت آن را بوسیله ضرایب همبستگی پیرسون و اسپیرمن نشان داد. در ادامه به وسیله یک مثال از مجموعه داده‌های SPSS، به شما نشان می‌دهیم که چگونه نموداری مشابه تصویر 2 ترسیم کنید.

نکته: توجه داشته باشید که اگر شرایط مربوط به محاسبه و تحلیل ضریب همبستگی اسپیرمن برقرار نباشد، شاخص‌های وابستگی دیگر مانند ضریب کندال قابل استفاده هستند. فقط دقت کنید که شرایط استفاده از هر یک این شاخص‌های وابستگی، چیست و چه زمانی به کار گرفته می‌شوند.

از ویژگی‌های مهم برای ضریب همبستگی اسپیرمن می‌توان به عدم حساسیت به نقاط پرت اشاره کرد. در این صورت اگر داده‌های زوجی شما، دارای نقاط پرت یا دور افتاده باشند، ضریب همبستگی پیرسون دچار مشکل شده و ممکن است ارتباط بین دو متغیر را بیشتر یا کمتر از مقدار واقعی برآورد کند، در حالیکه ضریب همبستگی اسپیرمن، به علت محاسبه وابستگی برحسب رتبه‌ها، دچار این مشکل نخواهد شد.

از طرفی وجود توزیع نرمال برای بدست آوردن ضریب همبستگی اسپیرمن، ضروری نیست. در حالیکه ضریب همبستگی پیرسون، با شرط وجود رابطه خطی و همچنین توزیع نرمال دو متغیره برای داده‌ها، بهتر عمل خواهد کرد. بنابراین اگر این دو شرط (خطی بودن و توزیع نرمال) وجود نداشته باشد، استفاده از ضریب همبستگی اسپیرمن ضروری خواهد بود.

در بخش بعدی با مثالی که براساس نمرات ۱۰ دانش آموز در درس ریاضی و انگلیسی ساخته شده، تحلیل ضریب همبستگی اسپیرمن را در SPSS دنبال خواهیم کرد. البته شرایط محاسبه و تحلیل را نیز مورد بررسی قرار خواهیم داد.

نمایش رابطه بین دو متغیر بوسیله نمودار پراکندگی

در این قسمت از یک فایل نمونه برای محاسبه و همچنین تحلیل ضریب همبستگی اسپیرمن در SPSS استفاده خواهیم کرد. به منظور دریافت فایل spearman correlation dataset، کافی است اینجا کلیک کنید تا فایل اطلاعاتی با قالب فشرده، روی رایانه شما، بارگذاری شود. پس از دریافت، این فایل را از حالت فشرده خارج کرده، سپس در نرم‌افزار SPSS، بارگذاری کنید.

فیلم آموزش تحلیل های رگرسیونی با اس پی اس اس SPSS در فرادرس

کلیک کنید

همچنین به منظور آشنایی با نحوه ورود داده‌ها و ویرایش خروجی‌های حاصل از نرم‌افزار SPSS، پیشنهاد می‌شود، نوشتارهای پنجره خروجی SPSS یا Output — راهنمای کاربردی و  پنجره ویرایشگر داده (Data Editor) در SPSS — راهنمای کاربردی مطالعه شوند.

این داده‌ها توسط یک معلم علاقه‌مند به آمار جمع‌آوری شده است. او می‌خواهد بداند که آیا دانش‌آموزان با نمره بالا در امتحان زبان انگلیسی، در ریاضیات نیز نتیجه بهتری می‌گیرند یا خیر. برای محک زدن این موضوع، معلم نمرات 10 دانش آموز خود را در امتحانات پایان سال برای هر دو درس زبان انگلیسی و ریاضیات ثبت کرده و در فایل spearman correlation dataset ذخیره کرده است. بر این اساس، یک متغیر مربوط به نمرات انگلیسی و یک متغیر هم نمرات ریاضیات برای 10 دانش آموز اختصاص یافته است.

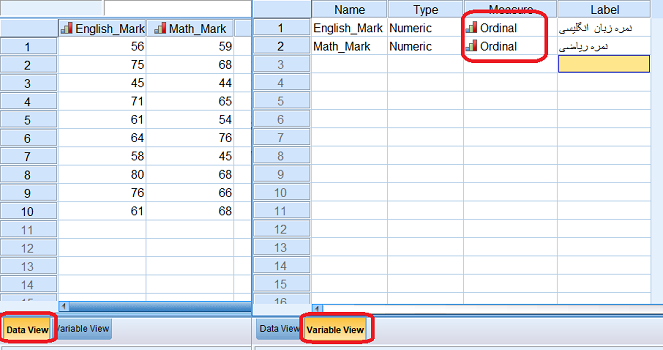
ابتدا به این فایل و متغیرهای موجود در آن نگاهی می‌اندازیم. همانطور که در تصویر ۳ مشاهده می‌کنید، داده‌ها در برگه Data View و متغیرهای در Variable View ظاهر خواهند شد. همانطور که مشخص است دو متغیر ایجاد کردیم تا بتوانیم داده‌های خود را وارد کنیم. مقادیر متغیر اول به نام English_Mark (یعنی نمرات انگلیسی) و متغیر دوم نیز به نام Maths_Mark (یعنی نمرات ریاضی) در این مجموعه داده به صورت دو ستون جداگانه ثبت شده است.

نکته: توجه داشته باشید که نمره (امتیاز) هر چند به صورت عدد بوده و کمی به نظر می‌رسد، ولی در حقیقت یک معیار برای رتبه‌بندی است. بنابراین می‌توانیم چنین داده‌هایی را از نوع ترتیبی (Ordinal) محسوب کنیم.

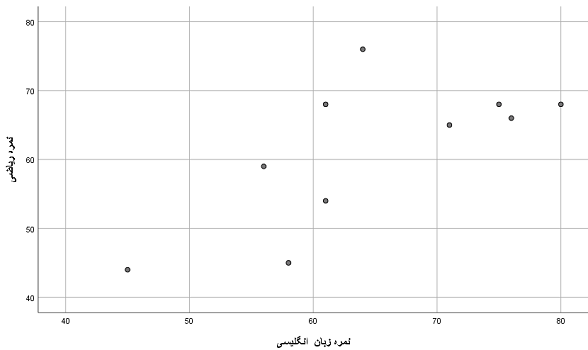
با توجه به داده‌های این مجموعه اطلاعاتی، به نظر می‌رسد که با افزایش نمره انگلیسی، نمره ریاضی نیز افزایش می‌یابد. برای نمایش چنین وضعیتی، بهتر است یک نمودار پراکندگی برای این دو متغیر ترسیم کنیم تا وضعیت وابستگی (یا همبستگی) بین آن‌ها را بهتر مشاهده کنیم. تصویر 4 چنین نموداری را نمایش داده است.

برای رسم آن کافی است که مراحل زیر را طی کنیم.

1. از فهرست Graph گزینه Legacy Dialog، سپس Scatter/Dot را انتخاب کنید.
2. در پنجره Scatter/Dot گزینه اول از سمت چپ، یعنی Simple Scatter را برای نمایش نمودار نقطه‌ای دو متغیره، انتخاب کرده و دکمه Define را کلیک کنید.
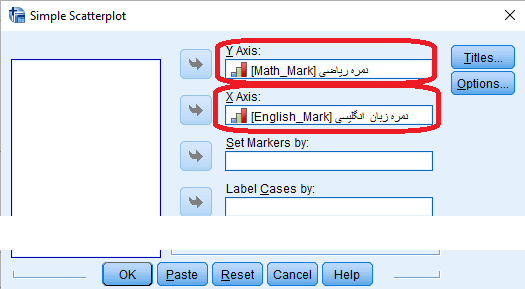
3. در پنجره Simple Scatterplot، تنظیمات را مطابق با تصویر 5 انجام دهید.

وجود رابطه مستقیم بین این دو متغیر در نمودار به خوبی دیده می‌شود. همانطور که مشخص است با افزایش نمره زبان انگلیسی (محور افقی) مقادیر مربوط به نمره ریاضی (محور عمودی) افزایش خواهد یافت و برعکس کاهش نمره انگلیسی باعث کاهش نمره ریاضی خواهد شد.

نکته: اگر می‌خواهید در محیط کدنویسی نرم‌افزار SPSS، چنین نموداری را ترسیم کنید، کافی است در پنجره Syntax، دستورات زیر را وارد کرده، سپس اجرا نمایید.

1GRAPH
2  /SCATTERPLOT(BIVAR)=English_Mark WITH Math_Mark
3  /MISSING=LISTWISE.

اجرای دستور تحلیل ضریب همبستگی اسپیرمن در SPSS

در صورتی که شرایط برای محاسبه ضریب همبستگی اسپیرمن محقق شده باشد، می‌توانیم همبستگی یا وابستگی بین زوج‌های داده را بوسیله این شاخص محاسبه کرده و مورد آزمون قرار دهیم. این کار را با طی کردن چهار گام یا مرحله انجام خواهیم داد. در گام آخر نیز نتایج حاصل از خروجی دستورات را مورد تفسیر قرار می‌دهیم.

گام اول: دسترسی به دستور محاسبه ضریب همبستگی

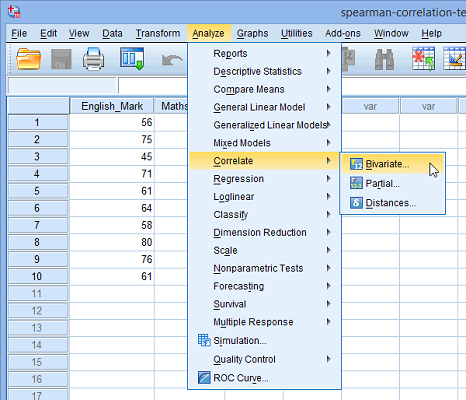
دسترسی به دستور محاسبه ضریب همبستگی در SPSS، اولین مرحله محسوب می‌شود. کافی است مسیر زیر را طی کنید.

Analyze - Correlate - Bivariate

البته، در تصویر 6 مسیر دسترسی به دستور محاسبه ضریب همبستگی را هم مشاهده می‌کنید. از آنجایی که به دنبال ضرایب همبستگی دو به دو هستیم، گزینه Bivariate یا دو متغیره را انتخاب کرده‌ایم.

نکته: گزینه Partial برای محاسبه ضریب همبستگی جزئی به کار می‌رود. برای مشاهده جزئیات بیشتر در این زمینه، مطلب ضریب همبستگی جزئی (Partial Correlation) — به زبان ساده را مطالعه کنید. از طرفی فاصله‌ها (Distance) نیز با توجه به توابع فاصله تعریف شده در SPSS در این بخش قرار دارند که در نوشتار فاصله اقلیدسی، منهتن و مینکوفسکی ــ معرفی و کاربردها در داده‌کاوی به چند شیوه معمول برای سنجش آن اشاره شده است.

گام دوم: تعیین پارامترها

پس از اجرای این دستور، پنجره‌ای به نام Bivairate Correlation باز شده که از شما پارامترهای مربوط به محاسبه ضرایب همبستگی را درخواست می‌کند. از آنجایی که به تحلیل ضریب همبستگی اسپیرمن در SPSS احتیاج داریم، تنظیمات این پنجره را مطابق با تصویر 7 انجام می‌دهیم.

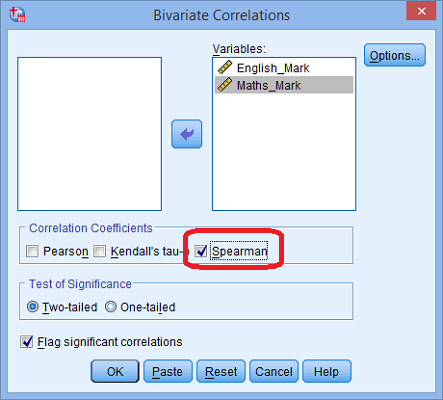
توجه داشته باشید که به منظور اجرای این دستور در محیط Syntax، کافی است دستورات زیر را در پنجره مربوطه وارد کرده و اجرا نمایید.

1DATASET ACTIVATE DataSet0.
2NONPAR CORR
3  /VARIABLES=English_Mark Math_Mark
4  /PRINT=SPEARMAN TWOTAIL NOSIG
5  /MISSING=PAIRWISE.
6            <div class="faradars-courses faradars-courses-single">
7                <a href="https://faradars.org/courses/fvst9408-correlation-and-linear-regression-with-spss?utm_source=blog.faradars&utm_medium=referral-post&utm_campaign=related-courses-inline-5&utm_term=a.reybod&utm_content=statistics" target="_blank">
8                    <div class="card card-course">
9                        <div class="card-image">
10                            <img class="pop-img" src="https://faradars.org/wp-content/uploads/2015/11/fvst9408-svg.svg" alt="آموزش همبستگی و رگرسیون خطی در اس پی اس اس SPSS">
11                        </div>
12                        <div class="card-body">
13                            <div class="card-title">
14                                فیلم آموزش همبستگی و رگرسیون خطی در اس پی اس اس SPSS در فرادرس
15                            </div>
16                        </div>
17                        <div class="card-action ml-3">
18                            <div class="fdb-btn">کلیک کنید</div>
19                        </div>
20                    </div>
21                </a>
22            </div>
23        

همانطور که در کد مشاهده می‌کنید، ضریب همبستگی اسپیرمن، یک ضریب همبستگی ناپارامتری (NONPAR CORR) در نظر گرفته شده. از آنجایی که گزینه Two-tailed را در پنجره تصویر ۷ و همچنین کد مربوطه انتخاب کرده‌ایم، آزمون دو طرفه (دو دنباله) برای ضریب همبستگی اجرا خواهد شد. به یاد دارید که ضریب همبستگی هر متغیر با خودش برابر با ۱ خواهد بود. بنابراین انتظار داریم قطر اصلی ماتریس ضریب همبستگی اسپیرمن، با مقادیر ۱ پُر شده باشند.

گام سوم: دریافت خروجی

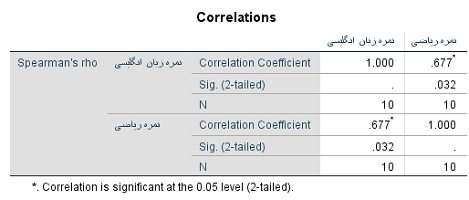
همانطور که در تصویر 8 مشاهده می‌کنید، مقدار ضریب همبستگی اسپیرمن بین دو متغیر نمره انگلیسی و نمره ریاضی، برابر با 0٫677 است که در سطح خطای ۰٫۰۵، فرض صفر که نشانگر عم رابطه یکنواخت بین دو متغیر است رد می‌شود. عدم رابطه یکنواخت در آزمون فرض به شکل صفر بودن ضریب همبستگی نشان داده می‌شود.

$$\large \begin{cases} H_0: & \rho_s = 0 \\ H_1: & \rho_s \neq 0 \end{cases}$$

گام چهارم: تفسیر خروجی حاصل

از آنجایی که مقدار Sig برای آزمون دو طرفه ($$2-tailed$$) برابر با ۰٫۰۳۲ بوده و از ۰٫۰۵ کوچکتر است، فرض صفر رد می‌شود. توجه دارید که ضریب همبستگی (هم ضریب پیرسون و هم ضریب اسپیرمن)، یک شاخص متقارن است، در نتیجه همبستگی بین متغیر نمره زبان با ریاضی، با همبستگی متغیر ریاضی با زبان برابر است. از آنجایی که ۱۰ مشاهده در نمونه، موجود است، محاسبه ضریب همبستگی اسپیرمن نسبت به ضریب همبستگی پیرسون که یک ضریب همبستگی پارامتری است، ترجیح دارد.

گزارش نتایج مربوط به این خروجی به صورت زیر در مقالات و نوشتارهای عملی ظاهر می‌شود. شما هم از همین شیوه برای تهیه گزارش تحقیقی خود بهره ببرید.

برای تعیین رابطه بین نمرات امتحانات انگلیسی و ریاضی 10 دانش آموز از همبستگی رتبه‌ای اسپیرمن استفاده شد. بین نمرات انگلیسی و ریاضیات همبستگی قوی و مثبتی وجود داشت که از نظر آماری معنی دار بود (rs  = 0٫667 ، p =۰٫032).

خلاصه و جمع‌بندی

در این نوشتار با تحلیل ضریب همبستگی اسپیرمن در SPSS آشنا شده و نحوه تفسیر آن را بازگو کردیم. همانطور که خواندید، به کارگیری و تحلیل ضریب همبستگی اسپیرمن در زمانی که نمی‌توان توزیع جامعه آماری را با توزیع نرمال یکی دانست یا داده‌ها از نوع رتبه‌ای باشند، مناسب است. به این ترتیب مشخص می‌شود که ضریب همبستگی اسپیرمن، براساس روش‌های ناپارامتری مورد تحلیل قرار می‌گیرد. البته توزیع آماره آزمون این شاخص آماری، به صورت مجانبی، نرمال است و به همین جهت، برای تحلیل آن از فاصله اطمینان و آزمون z استفاده می‌شود.