فرادرستجانس در هندسه — به زبان ساده
در آموزش‌های قبلی مجله فرادرس، انواع تبدیل‌های هندسی را معرفی کردیم. تبدیل هندسی، در واقع تابعی است که نقاط صفحه را به عنوان ورودی می‌گیرد و نقاط دیگری را در صفحه به عنوان خروجی نتیجه می‌دهد. به بیان ساده، می‌توان چنینن گفت که تبدیل قاعده‌ای است که به ما می‌گوید چگونه نقاط جدیدی ایجاد کنیم. تبدیلات هندسی را می‌توان در انواع انتقال، دوران، تجانس و بازتاب دسته‌بندی کرد. در این آموزش، با تجانس در هندسه آشنا می‌شویم.
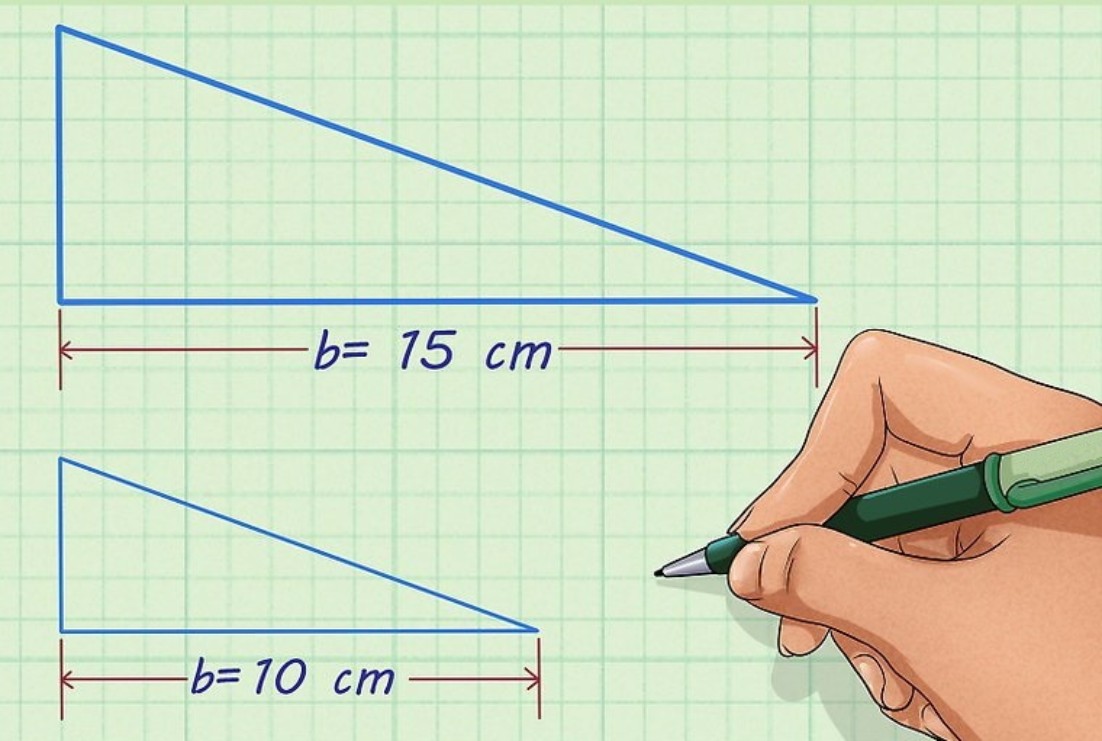
تعریف تجانس
تجانس در لغت به معنی هم‌جنس و هم‌شکل بودن است و در هندسه به مفهوم تغییر مقیاس اشکال هندسی است. تعریف تجانس در هندسه نیز چیزی غیر از این مفهوم نیست.
تعریف: فرض کنید $$O$$ یک نقطه ثابت در صفحه مختصات بوده و $$k\neq0$$ یک عدد حقیقی باشد. نقطه $$A'$$ را «مُجانس» نقطه $$A$$ به «مرکز» $$O$$ با «نسبت تجانس» $$k$$ می‌نامیم، در صورتی که سه شرط زیر برقرار باشند:
- سه نقطه $$O$$، $$A$$ و $$ A'$$ در امتداد یک خط راست باشند.
- فاصله $$A'$$ از $$O$$، مساوی با $$k$$ برابرِ فاصله $$ A $$ از $$O$$ باشد؛ یعنی $$OA'=|k|OA$$.
- اگر $$k$$ مثبت باشد، $$A'$$ روی نیم‌خط $$OA$$ و نقاط $$A$$ و $$A'$$ در یک طرف نقطه $$O$$ قرار دارند. همچنین، اگر $$k$$ منفی باشد، نقطه $$O$$ بین $$A$$ و $$A'$$ قرار خواهد گرفت.
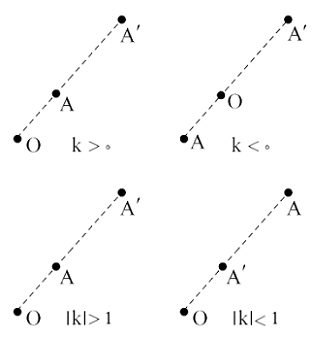
در تعریف بالا، اگر $$k> 0 $$ باشد، تجانس را «مستقیم» و اگر $$ k < 0 $$ باشد، تجانس را «معکوس» می‌نامیم. همچنین، اگر $$|k|<1$$ باشد، به آن تجانس «انقباض» می‌گوییم و در صورتی که $$|k|> 1 $$ باشد، تجانس «انبساط» نام دارد.
بنابراین، تجانس یک تبدیل است که نقطه $$O$$ در آن ثابت مانده و فاصله هر نقطه $$A$$ از مرکز در امتداد خط $$OA$$ در نسبت تجانس یا ضریب مقیاس $$k$$ (با در نظر گرفتن علامت آن) ضرب می‌شود و نقطه جدید $$A'$$ را تشکیل می‌دهد.
مثلث $$ \Delta ABC $$ زیر را در نظر بگیرید که حول نقطه $$P$$ با ضریب مقیاس ۲ توسعه یافته است. توجه کنید که نقاط $$ P$$، $$A$$ و $$A’$$ روی یک خط واقع شده‌اند. به طور مشابه، سه نقطه $$ P $$، $$B$$ و $$ B’ $$ و همچنین سه نقطه $$P$$، $$C$$ و $$ C’$$ نیز در امتداد یک خط هستند. در این شکل، $$PC=3$$ و $$PC’ = 6 $$ است. با توجه به $$ \frac { P C' } { P C } = \frac63 = 2 $$، ضریب مقیاس ۲ است. اگر سایر فواصل را نیز محاسبه کنیم، خواهیم دید که رابطه $$ \frac { P A' } { P A } = \frac { P C' } { P C } = 2 $$ برقرار است.
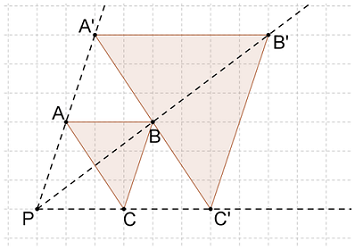
همان‌طور که می‌بینیم، در تجانس فوق، $$\Delta A’ B’ C’ $$ بزرگ‌تر از $$\Delta ABC$$ است و زوایا حفظ شده‌اند. شکل اصلی و تصویر بعد از تجانس متشابه خواهند بود، به این معنی که تصویر حاصل همان شکل را خواهد داشت و تنها اندازه‌ها تغییر می‌کنند. دو قضیه مهم زیر بیانگر این موارد هستند.
قضیه ۱: تجانس شیب را حفظ می‌کند.
قضیه ۲: تجانس اندازه زاویه را حفظ می‌کند.
مثال‌ها
در این بخش، چند مثال را برای درک بهتر مفهوم تجانس بیان می‌کنیم.
مثال ۱. رسم انبساط یک پاره خط
خط زیر را با در نظر گرفتن مرکز $$P$$ و ضریب تجانس 3 رسم کنید.
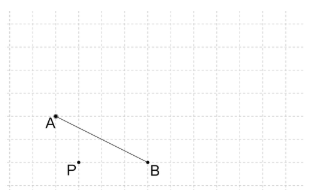
حل: برای رسم مجانس، از نقطه $$P$$، سه خط را رسم می‌کنیم که یکی از نقطه $$A$$، یکی از نقطه $$B$$ و دیگری از $$ C $$ عبور کنند. فاصله این خطوط از مرکز $$P$$ باید سه برابر فاصله نقطه اصلی تا $$P$$ در آن امتداد باشد. شکل زیر جواب این مثال است.
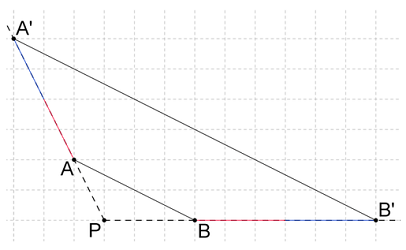
مثال ۲. رسم انقباض یک پاره خط
مجانس پاره خط زیر را برای مرکز $$P$$ و نسبت تجانس $$ \frac 12 $$ به دست آورید.
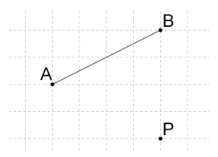
حل: فاصله $$P$$ تا $$A'$$ باید نصف فاصله $$ P $$ تا $$ A $$ باشد. به طور مشابه، فاصله $$P$$ تا $$ B' $$ نیز باید نصف فاصله $$P$$ تا $$B$$ باشد. شکل زیر، جواب این مثال است.
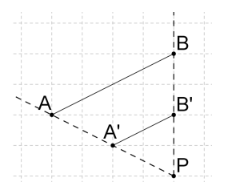
مثال ۳. بررسی ویژگی‌های تجانس
در مثال ۲، ثابت کنید روابط $$A'B' = \frac12 AB $$ و $$\overline{A'B'}|| \overline{AB}$$ برقرارند.
حل: با استفاده از قضیه فیثاغورس، دو طول مورد نظر را محاسبه می‌کنیم:
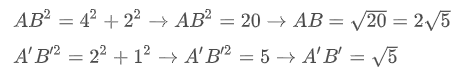
بنابراین، می‌بینیم که $$A'B'= \frac 12 AB$$. شیب دو پاره‌خط نیز برابر با $$ \frac 12 $$ است و در نتیجه، $$\overline{A'B'}|| \overline{AB}$$ نیز برقرار است.
اگر علاقه‌مند به یادگیری مباحث مشابه مطلب بالا هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:
- مجموعه آموزش‌های دروس ریاضیات
- آموزش جامع ریاضی دبیرستان – ریاضی و فیزیک
- مجموعه آموزش‌های دروس دبیرستان و پیش‌دانشگاهی
- آموزش ریاضیات عمومی 1
- مثلث، تعریف و محاسبات آن در هندسه — به زبان ساده
- فرمول هرون — به زبان ساده
- زاویه داخلی و محاسبات آن در اشکال چندضلعی — به زبان ساده
^^
