انتگرال توابع مثلثاتی – از صفر تا صد
پیشتر در وبلاگ فرادرس، مفاهیم پایهای انتگرال و روشهای محاسبه آن را بیان کردیم. اما در مواردی با انتگرالهایی روبرو هستیم که در بخشی از تابعِ تحت انتگرال، تابعی مثلثاتی وجود دارد. در این قسمت قصد داریم تا در قالب مثال، روشهای حل انتگرال توابع مثلثاتی را بیان کنیم.


مقدمه
در انتگرالهایی که در آنها از توابع مثلثاتی استفاده شده میتوان با استفاده از روابط مثلثاتی، تابع تحت انتگرال را به شکلی سادهتر نوشت. در مواردی نیز میتوان با نوشتن یک تابع در مختصات قطبی، تابع تحت انتگرال را بهشکل مثلثاتی نوشته و از آن انتگرال گرفت.
قبل از توضیح نحوه بدست آوردن انتگرال توابع مثلثاتی نیاز است تا با روابط مثلثاتی آشنا باشید. در این مطلب میتوانید این روابط را به خاطر بسپارید اما در آینده در مورد نحوه بدست آمدن آنها نیز بحث خواهد شد.
انتگرال توابع توانی
در ابتدا انتگرال توابعی را بیان میکنیم که در آنها از توانهای بالاتر توابع مثلثاتی استفاده شده است. در ابتدا در قالب چندین مثال بدست آوردن این نمونه از انتگرالها را توضیح میدهیم و در انتها روش کلی حل آنها را توضیح میدهیم.
مثال ۱
انتگرال تابع را بیابید.
پاسخ: معمولا انتگرالهایی که در آنها از توان چندم (توان ۲ به بالا) تابع مثلثاتی استفاده شده، میتوان از تغییر متغیر توابع پایه استفاده کرد. برای نمونه در این مثال میتوان از تغییر متغیر u=sin x استفاده کرد. با این فرض، دیفرانسیل du= cosx dx حاصل میشود. اما نکته اینجاست که در تابع تحت انتگرال، عبارت sin x موجود نیست. در چنین مواردی میتوان با استفاده از روابط مثلثاتی، عبارت مدنظر را ایجاد کرد. برای نمونه در این مثال مناسب است که از رابطه استفاده شود. در این صورت داریم:
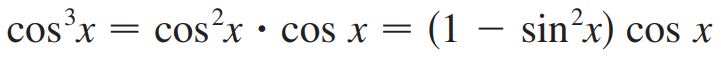
حال انتگرال را میتوان با استفاده از روش تغییر متغیر، بهشکل زیر بدست آورد.
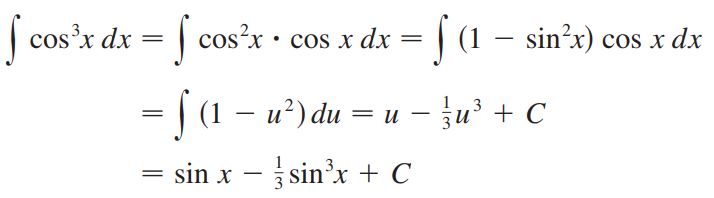
همانطور که در مثال بالا دیدید، در انتگرالهای توانی، بهتر است یکی از توابع پایه (سینوس، کسینوس یا تانژانت) به عنوان u در نظر گرفته شده و با سادهسازی توان، du را در عبارت تولید کرد. برای درک بهتر به مثال ۲ توجه فرمایید.

مثال ۲
حاصل انتگرال را بیابید.
پاسخ: در چنین انتگرالهایی، یکی از توابع بهعنوان u در نظر گرفته و تابع زیر انتگرال بر حسب آن نوشته میشود. اگر در این مثال در نظر گرفته شود، du=-sin xdx خواهد بود. در نتیجه بایستی در تابع زیر انتگرال توان اول سینوس را نگه داشته و مابقی تابع بر حسب u یا همان کسینوس نوشته شود. در نتیجه میتوان گفت:
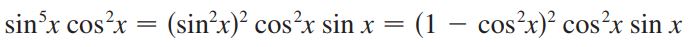
از طرفی بهمنظور استفاده از روش تغییر متغیر داریم:
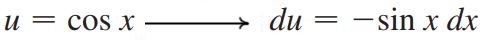
با فرض بالا، انتگرال مذکور به ترتیب زیر بدست میآید.
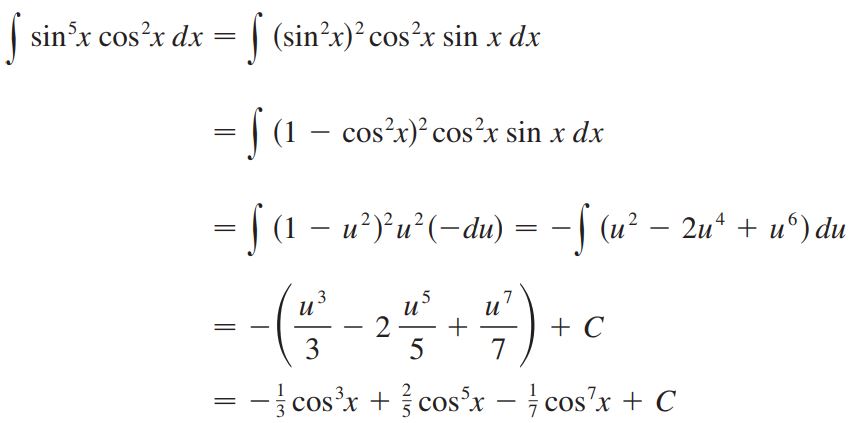
در دو مثال بالا، توان فرد سینوس یا کسینوس به ما اجازهی جدا کردن سینوس یا کسینوس را داد. در حالتی که توان هر دو تابع سینوس و کسینوس زوج باشد، نمیتوان از روش ارائه شده در مثال ۱ و ۲ استفاده کرد. بنابراین در مواردی که توانهای سینوس و کسینوسِ زیر انتگرال، زوج باشد، میتوان از قانون نصف کمان استفاده کرد.
با استفاده از قانون نصف کمان میتوان توانِ زوج عبارتهای سینوسی و کسینوسی را از بین برد. این قانون بهصورت زیر است.
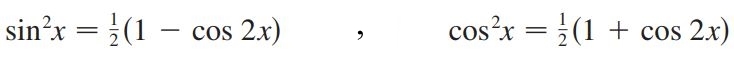
در مثالی که در زیر ارائه شده، از قانون نصف کمان استفاده شده است.
برای آشنایی با مباحث ریاضیات دبیرستان، پیشنهاد میکنیم به مجموعه فیلمهای آموزشهای دروس دبیرستان و پیش دانشگاهی فرادرس مراجعه کنید که لینک آن در ادامه آورده شده است.
- برای مشاهده مجموعه فیلمهای آموزشهای دروس دبیرستان و پیش دانشگاهی + اینجا کلیک کنید.
مثال ۳
حاصل انتگرال را بیابید.
پاسخ: در این مثال همچون مثال ۱ و ۲ نمیتوان از عبارت استفاده کرد؛ این انتگرال را میتوان با استفاده از قانون نصف کمان و بهترتیب زیر بدست آورد.
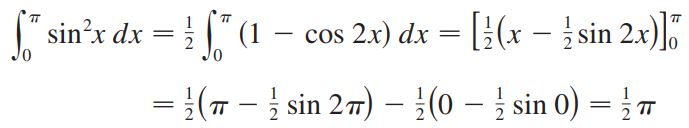
توجه داشته باشید که در پاسخ بالا از انتگرالِ استفاده شده است. البته در زیر مثالی زده شده که میتوانید با مطالعه آن نحوه بدست آوردن انتگرال توانهای بالاتر را فرا بگیرید.

مثال ۴
حاصل انتگرال را بیابید.
پاسخ: در این مثال توان چهارم ظاهر شده؛ در نتیجه بایستی دو بار از قانون نصف کمان استفاده کرد. با استفاده از این قانون، sin4 x بهصورت زیر در میآید.
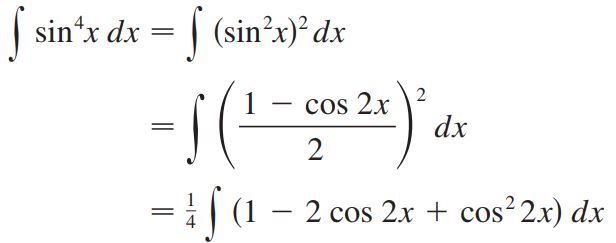
در عبارت بالا تابع Cos2 2x ظاهر شده؛ با اعمال قانون نصف کمان برای بار دوم داریم:
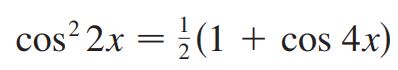
با جایگذاری رابطه بالا در رابطه ۱، توان سینوس کاملا از بین رفته و انتگرال بهترتیب زیر بدست میآید.
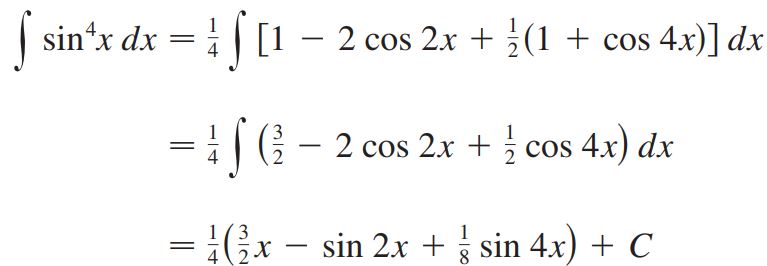
در ادامه بهطور خلاصه روش حل انتگرالِ بیان شده است.
مراحل بدست آوردن انتگرال
روش بهکار گرفته شده جهت محاسبه انتگرال، وابسته به فرد یا زوج بودن توانها است. در ادامه روش حل در هریک از این حالات توضیح داده شده است.
۱. توان کسینوس فرد باشد
اگر توان کسینوس فرد باشد (n=2k+1)، یکی از کسینوسها را نگه داشته و مابقی را با استفاده از رابطه ، بر حسب سینوس بیان میکنیم. با انجام این کارها حاصل انتگرال بهصورت زیر در میآید.
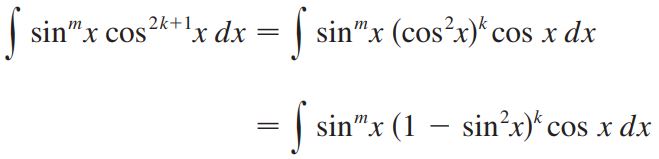
نهایتا از تبدیل u=sin x استفاده شده و پاسخ انتگرال بدست خواهد آمد.
۲. توان سینوس فرد باشد
در حالتی که توان سینوس فرد باشد، یکی از سینوسها نگه داشته شده و مابقی را با استفاده از تبدیل بیان میشوند. در حقیقت در این حالت انتگرال را میتوان بهشکل زیر بیان کرد:
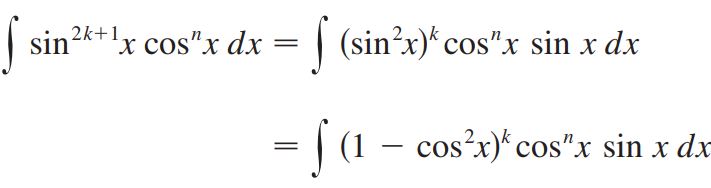
در مرحله بعد از تبدیل u=cos x استفاده کرده و آن را در رابطه بالا جایگذاری کنید. توجه داشته باشید که در حالتی که توان هردو فرد باشد، هر دو روش ۱ و ۲ را میتوان استفاده کرد.
۳. توان سینوس و کسینوس زوج باشد
در این حالت بایستی از قانون نصف کمان استفاده کرد.

در بعضی مواقع میتوان از قانون زیر نیز استفاده کرد.
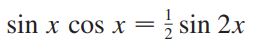
میتوان از استراتژی بالا بهمنظور محاسبه نیز استفاده کرد. توجه داشته باشید که رابطه بین دو تابع sec x و tan x بهصورت است. با مطالعه مثال زیر نحوه بدست آوردن انتگرال چنین توابعی را فرا خواهید گرفت.

مثال ۵
حاصل انتگرال را بیابید.
پاسخ: در ابتدا از تابع سکانت با توان دوم فاکتور گرفته و پس از آن از رابطه sec2 x=1+tan2 x استفاده میشود. پس از آن، با تغییر متغیر u=tan x، دیفرانسیل du=sec2xdx بدست میآید. نهایتا با جایگذاری این توابع در رابطه اصلی، به انتگرال زیر میرسیم.
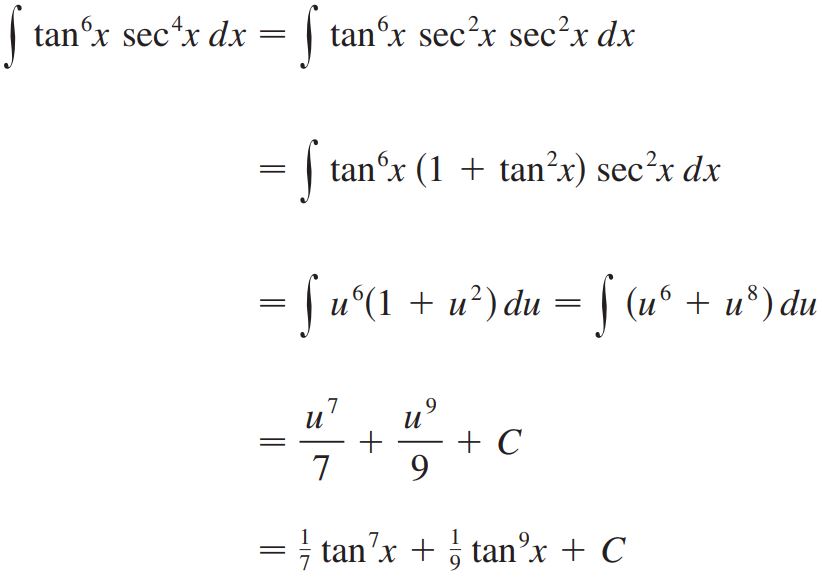
مثال ۶
حاصل انتگرال بیابید.
پاسخ: اگر از تابع فاکتور گرفته شود، آنچه از سکانت باقی میماند، تابع خواهد بود. این تابع را نمیتوان به آسانی به تانژانت تبدیل کرد. این در حالی است که با جدا کردن تابع مابقی را میتوان با استفاده از تبدیل به سکانت تبدیل کرد. نهایتا با در نظر گرفتن ، دیفرانسیل بدست میآید. با این فرض پاسخ انتگرال بهصورت زیر بدست خواهد آمد.
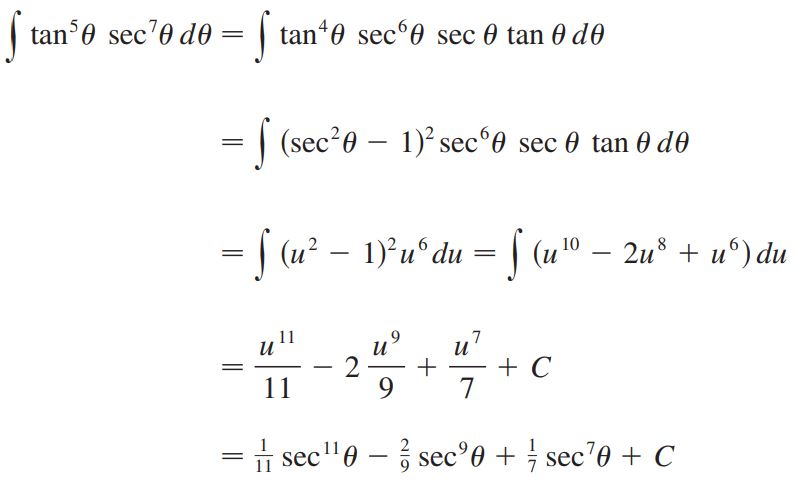
مثال ۵ و ۶ دو نمونه از انتگرالهایی محسوب میشوند که در آنها دو تابع تانژانت و سکانت در هم ضرب شده باشند. در ادامه استراتژی کلی حل اینگونه از مسائل بیان شده است.
مراحل بدست آوردن انتگرال
انتگرال tan x sec x نیز همچون حالت sin x cosx وابسته به توان است.
۱. توان سکانت زوج باشد
در این حالت از توان دوم سکانت فاکتور گرفته و مابقی را با استفاده از تبدیل بر حسب tan x بنویسید. با انجام این کار انتگرال بهصورت زیر در خواهد آمد.
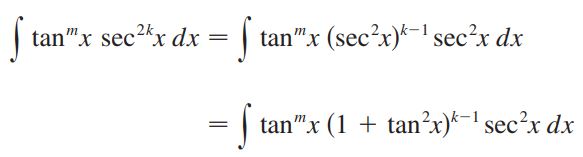
با نوشتن عبارت بالا و استفاده از تبدیل u=tan x، حاصل انتگرال نیز بدست خواهد آمد.
۲. توان تانژانت فرد باشد
اگر توان تانژانت فرد بود، از عبارت sec x tan x فاکتور گرفته و از تبدیل استفاده کنید. در نتیجه صورت انتگرال بهصورت زیر در خواهد آمد.
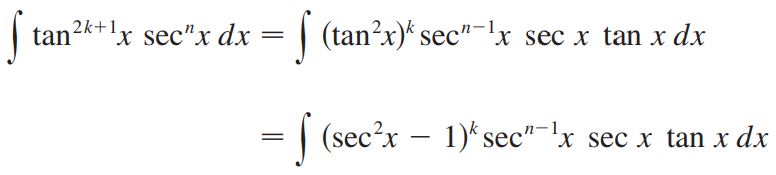
پس از انجام این کار، از تبدیل u= sec x استفاده کنید.
در مواردی غیر از دو حالت فوق، دستورالعمل مشخص وجود ندارد. البته در بسیاری از موارد میتوان با استفاده از روش جزء به جزء حاصل انتگرال را بدست آورد. در اکثر مواقع به انتگرال تانژانت خواهید رسید که حاصل آن برابر است با:
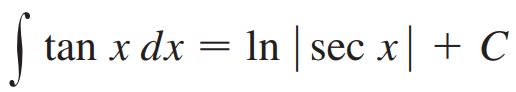
همچنین ممکن است با انتگرال سکانت روبهرو شوید که پاسخ آن برابر است با:
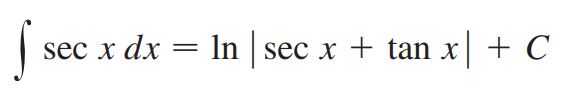
مثال ۷
حاصل انتگرال را بیابید.
پاسخ: همانطور که میبینید در این سوال توان تانژانت فرد است. بنابراین بایستی از توان ۱ تانژانت فاکتور گرفته سپس با استفاده از رابطه ، کل عبارت را به سِکانت تبدیل کنیم. در نتیجه انتگرال بهشکل زیر در میآید.
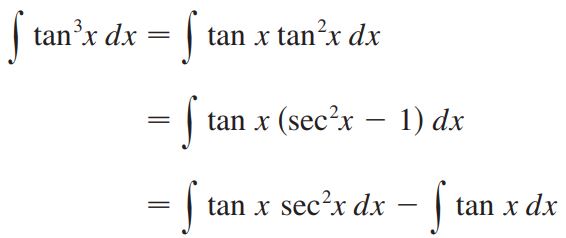
در مرحله بعدی از تبدیل u=tan x استفاده کرده و پاسخ انتگرال به ترتیب زیر بدست خواهد آمد.
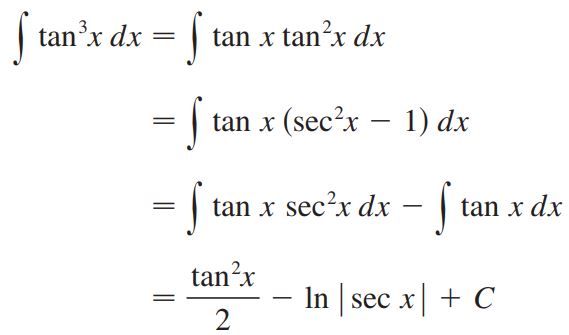
معمولا در مواردی که توان سکانت، فرد و توان تانژانت، زوج باشد، با نوشتن کل عبارت بر حسب سکانت، حاصل انتگرال را میتوان بدست آورد؛ همچنین با استفاده از روش جزء به جزء میتوان توان سکانت را از بین برد. برای نمونه به مثال زیر توجه فرمایید.

مثال ۸
حاصل انتگرال را بیابید.
پاسخ: با استفاده از انتگرال جزء به جزء داریم:
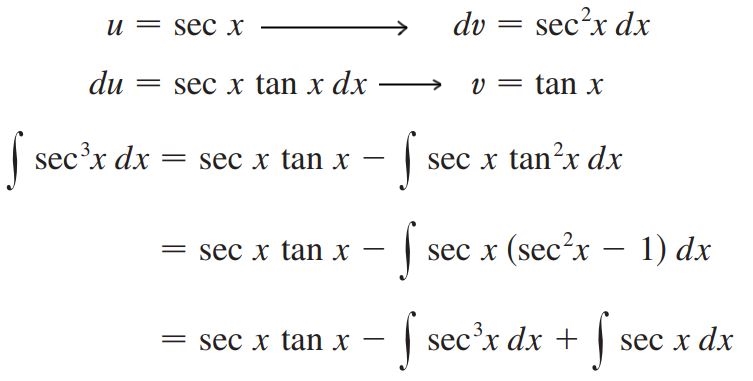
نهایتا با استفاده از رابطهی ۲ و همچنین عبارت بالا، حاصل انتگرال، برابر با تابع زیر بدست میآید.
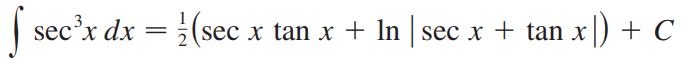
انتگرال توابع مثلثاتی ضرب شده
نمونهای دیگر از انتگرالهایی که ممکن است با آن مواجه شوید، انتگرال توابعی است که در آنها توابع سینوس و کسینوس با کمانهایِ بیشتر از واحد در هم ضرب شده باشند. در حقیقت مقصود ما انتگرالهایی بهصورت زیر است.
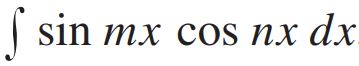
توجه داشته باشید که در رابطه بالا m و n اعداد صحیح هستند. جهت بدست آوردن چنین انتگرالهایی میتوانید به سادگی و با استفاده از روابط تبدیل ضرب به جمع که در زیر بیان شده، تابع زیر انتگرال را ساده کرده و انتگرالگیری را انجام دهید.
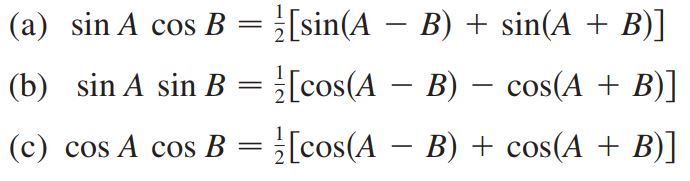
مثال زیر نحوه استفاده از روابط بالا را نشان میدهد.
مثال ۹
حاصل انتگرال را بیابید.
پاسخ: در ابتدا بایستی تابع زیر انتگرال را بهصورت حاصل جمع دو تابع بیان کرد. بهمنظور انجام این کار، میتوان از رابطه ۳ استفاده کرد. در نتیجه پاسخ نهایی برابر است با:
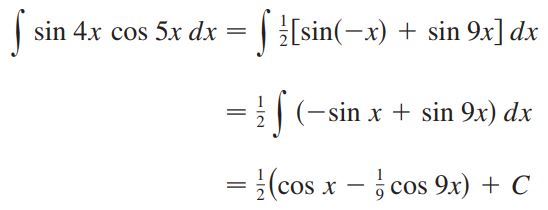
مثال ۱۰
حاصل انتگرال را بیابید.
پاسخ: جهت بدست آوردن پاسخ انتگرال مشابه با مثال 9 بایستی تابع تحت انتگرال را به جمع تبدیل کرد. با استفاده از تبدیل c در رابطه ۳، پاسخ انتگرال بهترتیب زیر بدست میآید.
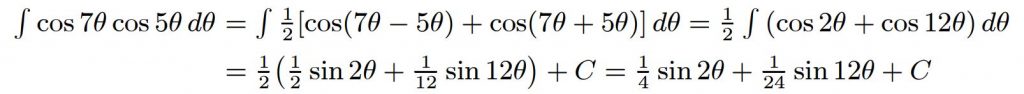
انتگرال توابع معکوس مثلثاتی
توجه داشته باشید که معمولا جهت محاسبه انتگرال توابع معکوس میتوان از انتگرالگیری جزء به جزء استفاده کرد.
در ادامه نحوه محاسبه انتگرال توابع معکوس مثلثاتی به روش جزء به جزء توضیح داده شده است.
تابع معکوس سینوس
همانطور که در بالا بیان شد، در مواجه با تابع معکوس مثلثاتی در ابتدا چک کنید و ببینید آیا میتوان آن را با استفاده از روش جزء به جزء حل کرد؟ هدف ما محاسبه انتگرال زیر است.
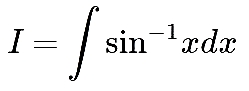
جهت بدست آوردن انتگرال فوق، تابع تحت انتگرال را میتوان بهصورت زیر تصور کرد.
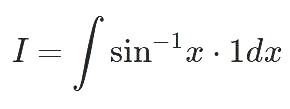
بهمنظور بهکارگیری روش جزء به جزء، عبارتهای u و dv بهصورت زیر در نظر گرفته میشوند.
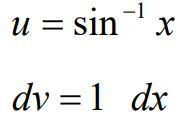
با این فرضیات، du و v بهصورت زیر در خواهند آمد.
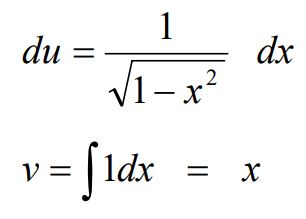
در نتیجه حاصل انتگرال با استفاده از روش جزء به جزء برابر است با:
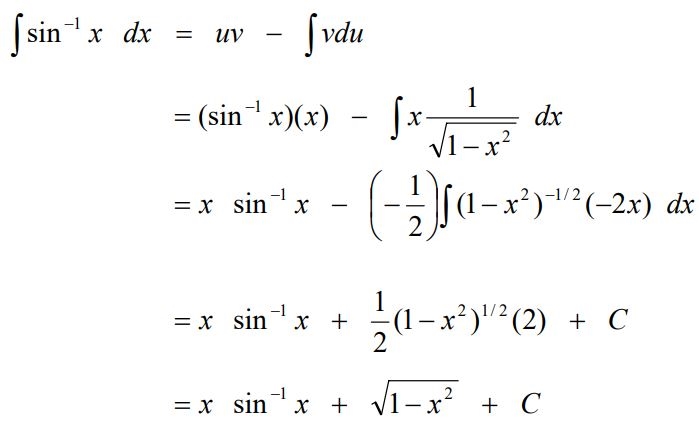

تابع معکوس کسینوس
جهت بدست آوردن انتگرالِ نیز از روش مشابه با انتگرال سینوس معکوس استفاده میشود.
در ابتدا u و dv را بهصورت زیر در نظر میگیریم.
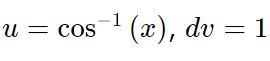
با این فرضیات، حاصل انتگرال برابر است با:
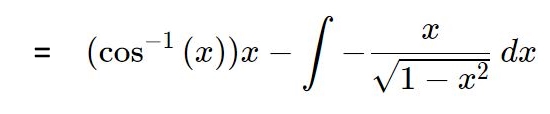
توجه داشته باشید که عبارت سمت راست در رابطه بالا را میتوان با استفاده از تغییر متغیر u=1-x2 بدست آورد. با استفاده از تغییر متغیر مذکور، انتگرال سمت چپ در رابطه بالا برابر است با:
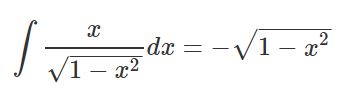
با استفاده از رابطه بالا پاسخ نهایی انتگرال تابع معکوس کسینوس برابر است با:
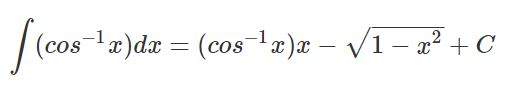
تابع معکوس تانژانت
بهمنظور بدست آوردن انتگرال تابع معکوس تانژانت نیز میتوان از روش جزء به جزء استفاده کرد. در قدم اول u و dv بهصورت u=tan-1x و dv=dx در نظر گرفته و جز به جز میگیریم. در نتیجه خواهیم داشت:
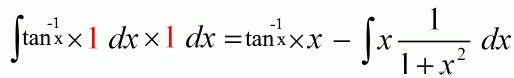
با فرض u=1+x2 انتگرال سمت راست در رابطه بالا نیز بدست خواهد آمد. در نتیجه پاسخ نهایی انتگرال معکوس تانژانت برابر است با:
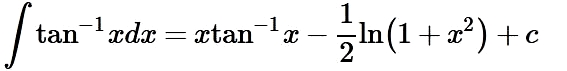
در جدول زیر حاصل انتگرال چند تابع معکوس مثلثاتی ارائه شده است.
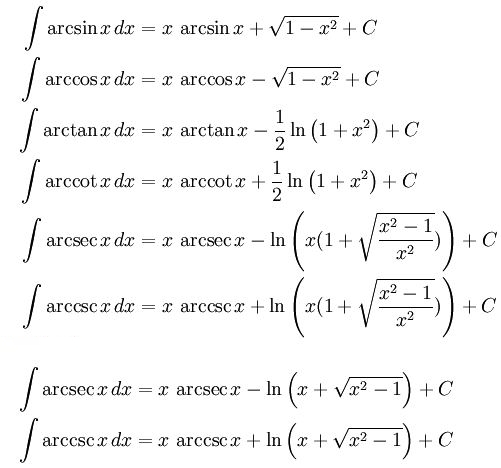
خلاصه
در این مطلب روشهایی ارائه شده که با استفاده از آنها میتوان انتگرال توابعی مثلثاتی که در یکدیگر ضرب شده یا به توان رسیدهاند را محاسبه کرد.
- در حالت توانی، سینوس یا کسینوس با توان ۱ جدا شده و مابقی بر حسب تابعِ دیگر نوشته میشوند (برای نمونه اگر سینوس جدا شد، مابقی بر حسب کسینوس نوشته میشوند).
- بهمنظور محاسبه انتگرال توابع مثلثاتی که در یکدیگر ضرب شدهاند، از روابط مثلثاتی مربوط به تبدیل ضرب به جمع استفاده میشود.
- در مواجه با انتگرال تابع معکوس مثلثاتی در ابتدا به روش جزء به جزء فکر کنید.
آزمون انتگرال توابع مثلثاتی
۱. کدام رابطه تریگونومتری بهترین روش برای سادهسازی پیش از انتگرالگیری است؟
برای سادهسازی عبارت "" پیش از انتگرالگیری، استفاده از رابطه "" یعنی قانون نصف کمان مناسبترین گزینه است. این رابطه را به شکلی تبدیل میکند که انتگرالش راحتتر محاسبه میشود.
۲. برای حل انتگرال ، چرا تشخیص فرد یا زوج بودن توانها اهمیت دارد؟
زیرا فقط برای توانهای فرد میتوان تغییر متغیر انجام داد.
چون تنها در توانهای زوج، توابع معکوس استفاده میشود.
چون با دانستن آن میتوان قانون نصف کمان یا سادهسازی مناسب را انتخاب کرد.
چراکه در هر حالتی باید تابع به ترکیب تانژانت و سکانت تبدیل شود.
کلید حل انتگرال در انتخاب استراتژی براساس فرد یا زوج بودن توانها است. زیرا برای حالت فرد، میتوان یکی از توابع را جدا کرده و با تغییر متغیر حل کرد و اگر هر دو زوج باشند، قانون نصف کمان بهترین راه است.
۳. در انتگرال عبارت ، اگر هر دو توان زوج باشند، کدام تکنیک باید به کار گرفته شود؟
از قانون نصف کمان برای سادهسازی استفاده میشود.
باید عبارت را به صورت ضرب به جمع تبدیل کنیم.
از فرمول مشتق tan(x) استفاده میشود.
روابط تغییر متغیر را به کار میبریم.
در حالتی که توان هر دو تابع سینوس و کسینوس در انتگرال مانند و زوج هستند، بهترین راهکار بهرهگیری از قانون نصف کمان است تا عبارات به سادهترین صورت برای انتگرالگیری تبدیل شوند. استفاده از روابط تغییر متغیر یا بهکارگیری مشتق تابع تانژانت مناسب این حالت نیستند، زیرا رویکرد مستقیم و سادهسازی را ارائه نمیدهند. تبدیل ضرب به جمع زمانی استفاده میشود که زوایا متفاوت باشند.
۴. در انتگرالهایی که ضرب سینوس با یک کمان در کسینوس با کمانی دیگر ظاهر میشود (مانند sin(kx) ضربدر cos(mx))، کدام روش برای سادهسازی و محاسبه انتگرال پیشنهاد شده است؟
استفاده از روش جز به جز
بهکارگیری تغییر متغیر قطبی
کاربرد قانون نصف کمان
استفاده از قانون تبدیل ضرب به جمع
زمانی که ضرب توابع سینوس و کسینوس با آرگومانهای متفاوت وجود دارد، «استفاده از قانون تبدیل ضرب به جمع» توصیه میشود، زیرا این تکنیک با تبدیل ضرب به جمع، محاسبه را بسیار سادهتر میکند.
۵. در انتگرالگیری تابع arctan(x) با روش جزء به جزء، چرا انتخاب درست u و dv میتواند روند حل را سادهتر کند؟
اگر x را به عنوان u بگیریم، مشتق پیچیده شده و حل مشکلتر میشود.
با انتخاب arctan(x) به عنوان u، مشتقگیری سادهتر انجام میشود و انتگرال dv به راحتی قابل محاسبه است.
اگر هر دو متغیر را همزمان تغییر دهیم، روند حل به طور قابل توجهی ساده نمیشود.
انتخاب arctan(x) به عنوان dv باعث دشواری انتگرالگیری و افزایش گامهای حل خواهد شد.
در روش جزء به جزء هنگام انتگرالگیری arctan(x)، اگر arctan(x) به عنوان u انتخاب شود مشتق آن است که بسیار سادهتر از مشتق x یا سایر انتخابهاست و انتگرال dv (یعنی dx) به راحتی بدست میآید.













سلام وقتتون بخیر
حاصلArccotxچندمیشه؟؟
با سلام و وقت بخیر؛
حاصل Arccot(x) به مقدار x بستگی دارد. در مطلب «آرک تانژانت چیست و چگونه محاسبه می شود؟ – به زبان ساده»، در مورد آرکتانژانت و رابطه با آن با آرک کتانژانت صحبت کردیم. علاوه بر این، حاصل آرک تانژانت چندین زاویه را نیز در یک جدول آوردیم. مطالعه این مطلب میتواند شما را در رسیدن به پاسخ سوالتان کمک کند.
از همراهی شما با مجله فرادرس سپاسگزاریم.
عذر خواهی میکنم آخرش میشه انتگرال
secxtanx+tan^2 xdx
انتگرال تابع 1/2^(a-tanx)/1 چی میشه؟
سلام
انتگرال dxبه
xضربدر رادیکال یک منهای ایکس به توان 4 را به روش جانشینی مثلثات برام حل کنید
سلام خیلی عالی . قبل از مثال هشت انتگرال تانژانت اشتباه گرفته شده . ممنون.
سلام و روز شما به خیر؛
مثال مورد نظر شما بازبینی شد، اما محاسبات صحیح است و موردی در آن مشاهده نشد.
از همراهی شما با فرادرس خرسندیم.
سلام میشه کمک کنین
انتگرال تانژانت(ال ان )
Tan(lnx)5x/x
سلامفرمول بازگشتی cotبه توان n رو میشه به دست بیارید ممنون
سلام وقت بخیر میخواستم بدونم جواب صحیح انتگرال تانژانت در (Lnx) تقسیم برx بعد کل معادله در dx چه میشود؟
سلام دمتون گرم خدا خیرتون بده
با سلام و خسته نباشید سالنو مبارک خیلی عالی ممنون از شما
فقط در مثال 3 جواب انتگرال که بدست می آیدقبل از جایگذاری بازه ها داخل کروشه نباید 1/2 هم در جمله اول که x باشد وهم در جمله دوم ضرب شود؟؟ یعنی جمله دوم بشود 1/4sin2x ؟
سلام مفید و کاربردی بود
مثال ۸ خط پنجم احتمالا ایراد داره
باید اینطور باشه:
انتگرال sec^3 xdx مساوی secx tanx منهای انتگرال secx+tan^2 xdx
طبق فرمول انتگرال fg مساوی Fg منهای انتگرال ‘Fg
سلام و وقت بخیر؛
بر اساس رابطه مثلثاتی بین تانژانت و سکانت، عبارت داخل انتگرال، باز شده است. سپس، انتگرال سکانت به توان سه، به طرف دیگر معادله انتقال داده شده است. مشکلی در این روش حل پیدا نشد.
از همراهی شما با مجله فرادرس سپاسگزاریم.
سلام. سال نو شما هم مباک.
مثال بررسی شد و حل آن صحیح است. ضریب ۱/۲ در پشت پرانتز قرار دارد و بر هر دو جمله اعمال شده است.
از همراهی شما سپاسگزاریم.
با سلام خدمت شما
من یک سوال داشتم چرا انتگرال منفی 1 بر روی رادیکال ۱ منهای ایکس ۲ برابر کسینوس اینورس ایکس هست اما انتگرال ۱ بر روی رادیکال ۱ منهای ایکس ۲ برابر سینوس اینورس هست؟!
چنین اتفاقی چجوری ممکن هست؟!
سپاس از شما. یاد جوانی ها افتادیم. خیلی خوب بود.
سلام.
فرمول صحیح ∫1–x2dx=arcsinx+C است. اگر انتگرالده را منفی کنید، حاصل انتگرال نیز منفی خواهد شد.
از همراهی شما با مجله فرادرس سپاسگزاریم.
خدا خیرتون بده خیلی مفید بودن.
سلام انتگرال آرک تانژانت یو تقسیم بر duچی میشه؟ دیه یو ÷(Arc tan(u
به روش جز به جز
Arctan(u)را Vگرفته و از du انتگرال میگیریم و ادامه میدهیم.
میشه انتگرال ۱/sin xرو حل کنین؟
با سلام و تشکر از بازخورد شما. این مسئله با استفاده از روش تغییر متغیر قابل است. هم میتوانید با ضرب کردن صورت و مخرج در sin x و هم با تقسیم کردن صورت و مخرج به Cos x)/2) از این روش استفاده کنید. در ادامه پاسخ مبتنی بر راهحل دوم ارائه شده است.
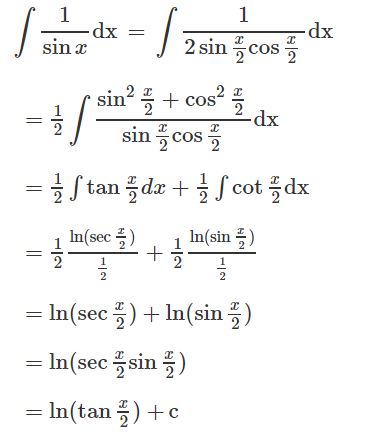
خیلی مفید و کامل بود.لایک!
خیلی خوب بود. واقعا دستتون درد نکنه