چارک چیست؟ – توضیح به زبان ساده با مثال
یکی از مفاهیم مهم در شاخه آمار توصیفی مبحث «چارک» (Quartile) است. چارک عبارت است از سه مقدار عددی که برای تقسیمبندی دادههای مرتب شده به چهار بخش بکار میروند، طوری که هر کدام از این بخشها دارای تعداد مساوی از مشاهدات باشند. چارکها نشاندهنده میزان تمایل مرکزی یا تنوع در یک مجموعه داده هستند و میتوان از آنها برای تقسیم یک توزیع احتمال به چهار بخش استفاده کرد، طوری که هر بخش احتمال برابری با دیگری داشته باشد. در این مطلب از مجله فرادرس یاد میگیریم که چارک چیست، مراحل محاسبه آن به چه صورت است و چگونه نمایش داده میشود. همچنین با حل و بررسی مثالهای مختلف، به شما کمک میکنیم تا درک بهتری از این ابزار توصیفی در آمار بهدست آورید.
- میآموزید چارک چیست و چگونه مجموعه دادهها را به چهار بخش تقسیم میکند.
- میتوانید مراحل محاسبه چارک اول تا سوم را از روی دادهها اجرا کنید.
- میآموزید چگونه چارکها را با مثال و روش عددی محاسبه کنید.
- میتوانید نمودار جعبهای (Boxplot) را رسم کرده و چارکها را روی آن نمایش دهید.
- درک میکنید تفاوت چارک با صدک و چندک چیست و چگونه استفاده میشود.
- میتوانید با استفاده از اکسل یا دادههای گروهبندیشده، چارکها را محاسبه کنید.


چارک چیست؟
در یک نمونه یا در یک مجموعه داده، چارک معادل است با سه مقدار عددی که دادهها را به چهار گروه با تعداد مشاهدات برابر تقسیمبندی میکند. اگر توزیع احتمال داشته باشیم، چارک بازه این توزیع را به چهار فاصله با احتمال مساوی تقسیمبندی میکند. سه مقدار عددی چارک بهترتیب برابر هستند با چارک اول یا چارک پایین، چارک دوم یا میانه و چارک سوم یا چارک بالا. از چارکها برای اطلاع از شکل توزیع و نحوه پخششدن دادهها استفاده میشود.
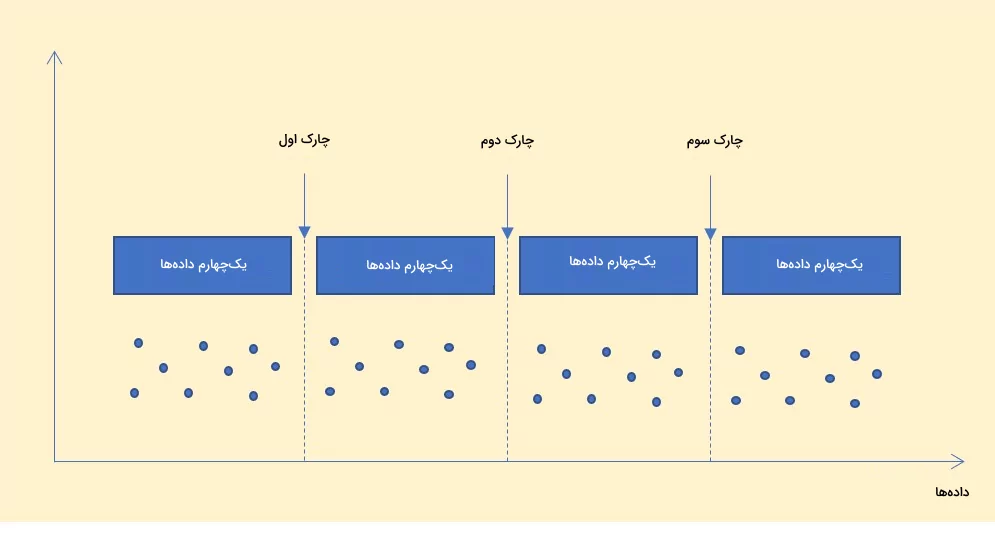
فرض کنید مقداری داده دارید که پس از مرتبسازی بر اساس کمترین مقدار تا بیشترین مقدار، کاملا میدانید کمترین مقدار، بیشترین مقدار و عددی که در جایگاه وسط این دادهها قرار میگیرد، چه هستند. در این صورت سه چارک را میتوانیم به شکل زیر تعریف کنیم:
- چارک اول که با Q۱ یا چارک پایینتر هم شناخته میشود، عددی است که دقیقا بین کمترین مقدار و عدد وسط قرار میگیرد.
- چارک دوم یا Q۲ را میانه هم مینامند که عدد وسط بین کمترین و بیشترین مقدار در نظر گرفته میشود.
- چارک سوم یا Q۳ که چارک بالاتر هم نامیده میشود، عددی است که بین عدد وسط و بیشترین مقدار قرار میگیرد.
در ادامه با توضیح یک مثال ساده یاد میگیریم که مراحل یافتن چارک چیست و از چه فرمولهایی برای پیدا کردن چارکهای اول تا سوم میتوانیم استفاده کنیم.
مسیر یادگیری آمار و احتمال با فرادرس
در بخش قبل تقریبا متوجه شدیم تعریف چارک چیست. پیش از اینکه به ادامه یادگیری مفهوم چارک در آمار بپردازیم، در این بخش میخواهیم یک مسیر یادگیری در شاخه آمار و احتمال به شما پیشنهاد دهیم. در فرادرس، چندین فیلم آموزش بر اساس عناوین کتابهای درسی ریاضی تهیه شده است. بنابراین شما میتوانید با مشاهده این فیلمهای آموزشی مسیر یادگیری خود را هموارتر کنید. توضیح مبحث آمار و احتمال از فصل نهم کتاب ریاضی پایه هفتم شروع میشود و تا پایه دوازدهم تقریبا در هر مقطع و رشتهای بخشی از مباحث این شاخه توضیح داده شده است. بنابراین اگر دانشآموز هستید و میخواهید تسلط کاملی بر کلیه مطالب مربوط به آمار و احتمال در مقطع متوسطه داشته باشید، عناوین پیشنهادی در لیست زیر را بهترتیب مشاهده کنید:
همچنین در کتاب درسی ریاضی دهم رشته علوم انسانی مفهوم چارک و دامنه میانچارکی توضیح داده شده است. مشاهده فیلم آموزش مربوط به این دوره نیز یادگیری شما را عمیقتر خواهد کرد:
- فیلم آموزش رایگان نمایش داده ها ریاضی پایه دهم علوم انسانی فرادرس
- فیلم آموزش ریاضی و آمار ۱ پایه دهم علوم انسانی فرادرس
- فیلم آموزش ریاضی و آمار ۱ پایه دهم به همراه حل سوالات کنکور فرادرس
- فیلم آموزش ریاضی و آمار ۲ پایه یازدهم علوم انسانی
مراحل محاسبه چارک
پس از اینکه تا حدی یاد گرفتیم سه مقدار عددی چارک چه نام دارند و چگونه تعریف میشوند، در این بخش در قالب یک مثال خیلی ساده، نشان میدهیم که گامهای یافتن چارک چیست. دقت کنید مراحل این بخش در شرایطی کاربرد دارند که بخواهیم چارک را برای یک نمونه یا یک مجموعه داده پیدا کنیم.
مثلا فرض کنید چند داده عددی شامل یک عدد ۱۲، یک عدد ۸، سه عدد ۹، یک عدد ۴، سه عدد ۵ و دو عدد ۲ داریم. یعنی در مجموع ۱۱ عدد داریم که برخی از این اعداد هم تکراری هستند. میخواهیم چارکها را برای این مجموعه داده پیدا کنیم. طبق مراحل زیر پیش میرویم:
- مرحله اول: شمارش دادهها
- مرحله دوم: مرتبسازی دادهها
- مرحله سوم: تعیین چارک اول
- مرحله چهارم: تعیین چارک دوم
- مرحله پنجم: تعیین چارک سوم
در شکلهای بخشهای بعدی، سه چارک موردنظر برای مجموعه دادهای که مثال میزنیم توسط دایرههای سبز رنگی مشخص شدهاند. اما بیاید مرحله به مرحله به هر کدام از این سه دایره سبز دست پیدا کنیم.
مرحله اول: شمارش دادهها
اولین مرحله شمارش تعداد مشاهدات یا دادههایی است که در اختیار داریم. عدد نهایی را با n نشان میدهیم. همانطور که اشاره شد، در این مثال ما تعداد n = ۱۱ داده داریم.
مرحله دوم: مرتبسازی دادهها
دومین مرحله برای اینکه بتوانیم تشخیص دهیم چارک چیست، این است که دادهها را به شکل زیر مرتب کنیم. منظورمان از مرتبسازی دادهها این است که آنها را بهترتیب از سمت چپ به راست از کمترین مقدار به بیشترین مقدار بنویسیم. پیش از اینکه مرحله سوم را توضیح دهیم، اگر دانشجو هستید و تمایل دارید پایه خود را در مورد مباحث آمار و احتمال قوی کنید، پیشنهاد میکنیم فیلم آموزشی آمار و احتمال مهندسی فرادرس را که لینک آن در ادامه برای شما قرار داده شده است، مشاهده کنید:

مرحله سوم: تعیین چارک اول
حالا میخواهیم ببینیم اولین چارک چیست. طبق تعریف، چارک اول یا پایینتر آن دادهای است که دقیقا بین کمترین مقدار و عدد وسط قرار دارد. در اینجا فرمولی برای پیدا کردن Q۱ بیان میکنیم که بهراحتی بتوانید آن را تشخیص دهید:
با محاسبه عبارت بالا عددی بهدست خواهد آمد که یکی از دو حالت زیر را خواهد داشت:
- اگر حاصل یک عدد صحیح شود، در این صورت چارک اول برابر است با میانگین اعداد در موقعیتهای و .
- اگر حاصل یک عدد صحیح نشود، در این صورت این عدد باید به سمت بالا گرد شود. حاصل نشاندهنده شماره جایگاه یا موقعیتی است که چارک پایینتر در آن قرار دارد.
دقت کنید عدد صحیح عددی است که بدون بخش اعشاری یا کسری نوشته شود. برای مثال ۱، ۰، ۲- اعداد صحیح هستند ولی ۱٫۲ عدد صحیح محسوب نمیشود. اگر به مجموعه دادهای که انتخاب کرده بودیم، بازگردیم، اول باید را محاسبه کنیم که میشود:
۲٫۷۵ یک عدد صحیح نیست. پس طبق دومین حالت، باید این عدد را گرد کنیم. گرد شده این عدد به سمت بالا، برابر با ۳ خواهد شد. پس سومین جایگاه از سمت چپ را بهعنوان Q۱ در نظر میگیریم که برابر میشود با عدد ۴.
مرحله چهارم: تعیین چارک دوم
برای اینکه ببینیم میانه یا دومین چارک چیست، ابتدا را محاسبه میکنیم که حاصل آن ممکن است دو حالت داشته باشد:
- اگر حاصل یک عدد صحیح شود، در این صورت چارک دوم برابر است با میانگین اعداد در موقعیتهای و .
- اگر حاصل یک عدد صحیح نشود، در این صورت این عدد باید به سمت بالا گرد شود. حاصل نشاندهنده شماره جایگاه یا موقعیتی است که چارک دوم در آن قرار دارد.
در مثال ما، مقدار برابر خواهد شد با . عدد ۵٫۵ یک عدد صحیح نیست، پس باید به سمت بالا گرد شود. حاصل ۶ خواهد شد، به این معنا که چارک دوم در ششمین جایگاه از سمت چپ قرار میگیرد. در نتیجه مقدار چارک دوم میشود ۵.
مرحله پنجم: تعیین چارک سوم
بهعنوان آخرین مرحله برای تعیین اینکه چارک چیست، اگر عدد بین بیشترین مقدار و عدد وسط را پیدا کنیم، چارک بالاتر یا چارک سوم هم مشخص شده است. اما با فرمول دقیقتر میتوانیم این عدد را پیدا کنیم. ابتدا را محاسبه میکنیم و با توجه به حاصل آن، یکی از دو روش زیر را ادامه میدهیم:
- اگر حاصل یک عدد صحیح شود، در این صورت چارک سوم برابر است با میانگین اعداد در موقعیتهای و .
- اگر حاصل یک عدد صحیح نشود، در این صورت این عدد باید به سمت بالا گرد شود. حاصل نشاندهنده شماره جایگاه یا موقعیتی است که چارک بالاتر در آن قرار دارد.
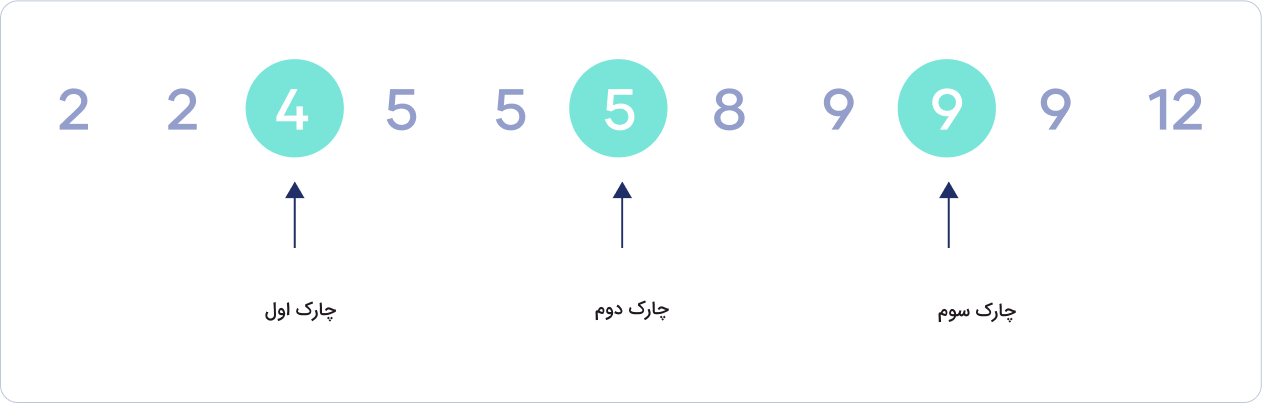
در مجموعه داده انتخابی ما، حاصل برابر است با . اگر این عدد به سمت بالا گرد شود، حاصل ۹ خواهد شد. بنابراین نهمین جایگاه در مجموعه اعداد ما از سمت چپ متعلق به چارک سوم است. پس Q۳ = ۹. این نکته را فراموش نکنید که گرد کردن همیشه به سمت بالا انجام میشود. دقت کنید طبق تعریف اول نوشته، دیدیم که چارکها مجموعه دادههای ما را به چهار بخش مساوی تقسیمبندی کردند، طوری که در هر بخش تعداد دادهها یا تعداد مشاهدات مساوی داریم (در هر بخش ۲ داده داریم).
همچنین ذکر این نکته ضروری بنظر میرسد که توافق جهانی برای بهترین راه تعیین چارکها وجود ندارد. پیش از اینکه به ادامه یادگیری و بررسی مثالها بپردازید، پیشنهاد میکنیم اگر دانشآموز پایه دهم هستید، به مطلب «فرمول های ریاضی دهم در یک نگاه و با مثال» از مجله فرادرس مراجعه کنید. در این نوشته کلیه فرمولهای کتاب ریاضی دهم از جمله روابط مربوط به فصل هفتم - آمار و احتمال برای شما جمعآوری شده است که بهعنوان یک منبع بسیار کاربردی است.
مثال تعیین چارکهای یک مجموعه داده
پس از اینکه یاد گرفتیم مراحل تعیین چارک چیست، در این بخش مثالهایی را در این زمینه حل میکنیم تا با روند محاسبات چارک کاملا آشنا شوید. اما پیش از آن قصد داریم فیلم آموزشی یادگیری ماشین و پیاده سازی در پایتون Python فرادرس را به شما معرفی کنیم که در آن مفهوم چارک بهمنظور کار با دادهها و کاربرد در یادگیری ماشین توضیح داده شده است. لینک این آموزش در ادامه برای شما قرار داده شده است:
مثال ۱
فرض کنید مطالعهای در زمینه میزان پیشرفت زبانآموزی روی بچههای ۱ تا ۶ سال داشتهاید و بخشی از دادههای خود را در جدول زیر جمعآوری کردهاید. حالا میخواهید مقالهای در این مورد بنویسید و چارکهای سن بچهها را گزارش دهید:
| سن (سال) | ۱ | ۲ | ۳ | ۴ | ۵ | ۶ |
| فراوانی | ۲ | ۳ | ۴ | ۱ | ۲ | ۲ |
پاسخ
همانطور که گفتیم اولین مرحله برای اینکه ببینیم چارک چیست، شمارش دادهها است. در این مثال شمارش تعداد مشاهدات باید انجام شود، یعنی باید فراوانی هر داده در نظر گرفته شود. برای نمونه، دو نفر در سن ۵ سال به زبان آموزی پرداختهاند، در حالی که در سن ۴، تنها یک نفر مطالعه زبان داشته است. پس دادههای ما بهصورت زیر خواهند بود:
n = ۲ + ۳ + ۴ + ۱ + ۲ + ۲ = ۱۴
مرحله بعدی این است که مشاهدات خود را بر اساس کمترین مقدار تا بیشترین مقدار مرتب کنیم. با توجه به جدولی که در اختیار داریم، مشاهدات به این شکل است که برای مثال دو عدد ۱ داریم، سه عدد ۲، چهار عدد ۳ و به همین ترتیب، که به شکل زیر نوشته میشوند:
۶ - ۶ - ۵ - ۵ - ۴ - ۳ - ۳ - ۳ - ۳ - ۲ - ۲ - ۲ - ۱ - ۱
نوشتن دادههای مرتب شده برای تعیین موقعیت یا جایگاه اعداد در مراحل بعد خیلی مهم است. حالا میرویم سراغ پیدا کردن چارک اول. گفتیم برای یافتن Q۱ اول باید را پیدا کنیم:
۳٫۵ عدد صحیح نیس، پس به سمت بالا گرد میشود و حاصل ۴ خواهد شد. بنابراین دنبال چهارمین عدد در دادهها مرتب شده بالا میگردیم که برابر است با ۲. بنابراین چارک اول یا Q۱ برابر است با ۲ سال. برای تعیین چارک دوم از فرمول زیر استفاده میکنیم:
۷ یک عدد صحیح است. پس چارک دوم برابر میشود با میانگین اعدادی که در موقعیتهای هفتم () و هشتم () قرار میگیرند. هفتمین عدد از مجموعه دادههای مرتب شده از سمت چپ برابر است با عدد ۳. هشتمین عدد هم برابر است با ۳. در نتیجه میانگین این دو عدد برابر خواهد شد با:
نکته: میدانیم میانگین m عدد مختلف برابر است با حاصل جمع آن اعداد تقسیم بر m.
پس Q۲ که همان میانه است، برابر شد با ۳ سال. در نهایت چارک سوم یا چارک بالا را با شروع از فرمول زیر پیدا میکنیم:
گرد شده عدد ۱۰٫۵ به سمت بالا برابر است با ۱۱. پس یازدهمین جایگاه در مجموعه دادههای مرتب شده برابر خواهد شد با چارک سوم که میشود ۵ سال.
مثال ۲
فرض کنید قد ۱۱ قورباغه بر حسب سانتیمتر بهصورت زیر اندازهگیری شده است. چارک سوم قد قورباغهها چقدر است؟
۷ - ۶٫۴ - ۷٫۳ - ۷٫۶ - ۶٫۸ - ۶٫۹ - ۷٫۱ - ۷٫۳ - ۵٫۹ - ۸٫۲ - ۶٫۹
پاسخ
با توجه به مراحل پیدا کردن چارکها، برای یافتن چارک سوم میتوانیم مستقیم از فرمول استفاده کنیم. با این فرض که در اینجا n = ۱۱ است:
حاصل عدد صحیح نیست. بنابراین باید ۸٫۲۵ را به بالا گرد کنیم که میشود ۹. مرحله بعدی پیدا کردن نهمین جایگاه در دادههای مرتب شده است. اما اول باید دادهها را از کوچکترین مقدار به بزرگترین مقدار مرتب کنیم:
۸٫۲ - ۷٫۶ - ۷٫۳ - ۷٫۳ - ۷٫۱ - ۷ - ۶٫۹ - ۶٫۹ - ۶٫۸ - ۶٫۴ - ۵٫۹
نهمین جایگاه در اعداد بالا مربوط میشود به عدد ۷٫۳. پس Q۳ = ۷٫۳ cm.
مثال ۳
هفت نفر در حال بازی با تاس هستند و فراوانی امتیازات آنها در جدول زیر نشان داده شده است. اولین چارک چیست؟
| امتیازات | ۰ | ۱ | ۲ | ۳ | ۴ | ۵ |
| فراوانی | ۱ | ۱ | ۲ | ۲ | ۰ | ۱ |
پاسخ
اولین قدم این است که تعداد دادهها یا n را بنویسیم. در این سوال هر عدد یک فراوانی دارد. برای مثال امتیاز ۰ فراوانی یک دارد، در حالی که امتیاز ۲ فراوانی دو دارد. این یعنی در نوشتن دادههای خود لازم است عدد ۲ را دو بار بنویسیم. پس دادههای ما به شکل زیر خواهند بود که خود به خود مرتب شده هم هستند:
۵ - ۳ - ۳ - ۲ - ۲ - ۱ - ۰
پس n = ۷. چارک اول با فرمول زیر بهدست میآید:
۱٫۷۵ عدد صحیح نیست و گرد شده آن میشود ۲. پس دومین جایگاه نشاندهنده چارک اول است، یعنی Q۱ = ۱.
تمرین
زمان دویدن ۶ دونده پس از طی مسافتی حدود ۵ km بر حسب دقیقه بهصورت زیر بوده است. چارک دوم زمان دویدن دوندهها کدام گزینه است؟
۳۴ - ۲۸ - ۳۱ - ۴۵ - ۳۵ - ۳۸
۳۴
۳۵
۳
۳۴٫۵
گزینه آخر درست است. در این سوال n = ۶ است. محاسبه چارک دوم با فرمول زیر انجام خواهد شد:
حاصل عدد صحیح ۳ شد. پس چارک دوم برابر است با میانگین اعدادی که در موقعیتهای ۳ و ۴ قرار میگیرند. ابتدا باید دادهها را مرتب کنیم تا موقعیت صحیح دادههای خود را بدانیم:
۴۵ - ۳۸ - ۳۵ - ۳۴ - ۳۱ - ۲۸
موقعیت ۳ معادل عدد ۳۴ است و موقعیت ۴ معادل ۳۵. میانگین این دو عدد را حساب میکنیم:
پس Q۲ = ۳۴٫۵ min است.
تعیین چارکها بر اساس صدک
در بخش قبل کاملا یاد گرفتیم که برای یک مجموعه داده، مراحل تعیین چارک چیست. همچنین توضیح دادیم که چارک نهتنها برای تقسیمبندی یک مجموعه داده بکار میرود، بلکه میتواند یک توزیع احتمال را نیز به چهار بخش با احتمالات مساوی جداسازی کند. اما امکان پیادهسازی مراحل بخش قبل برای توزیعهای احتمال وجود ندارد. پس لازم است به شیوه دیگری چارکها را برای توزیع احتمال تعیین کنیم.
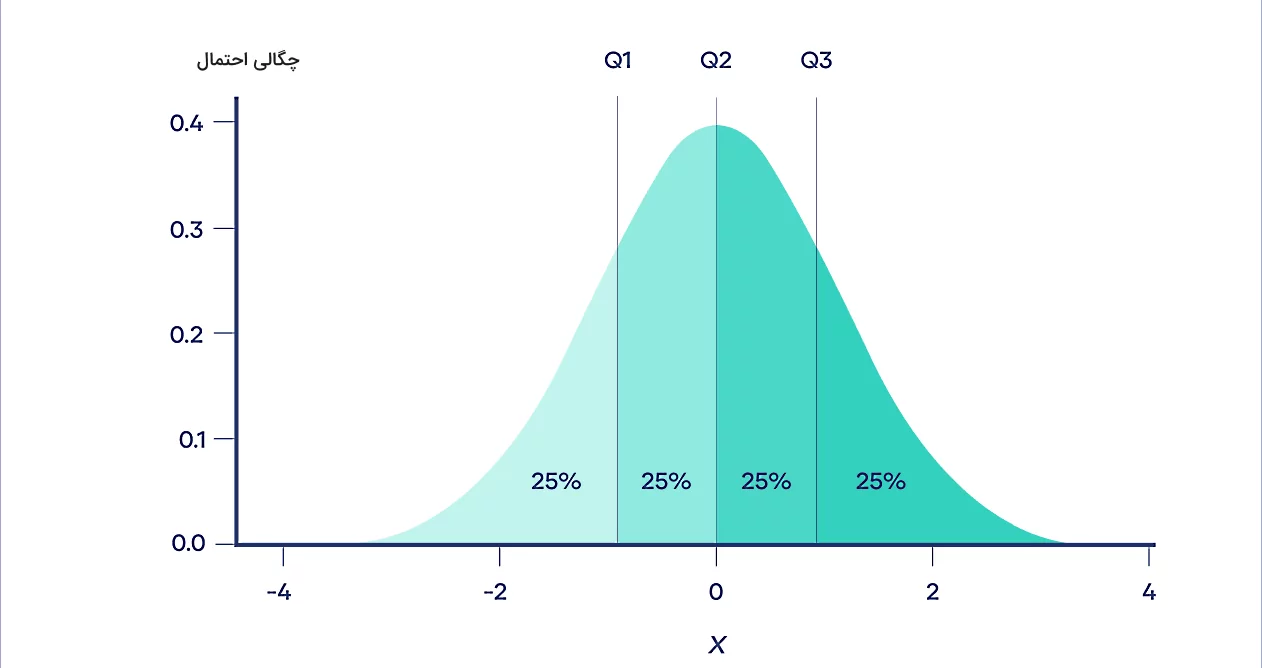
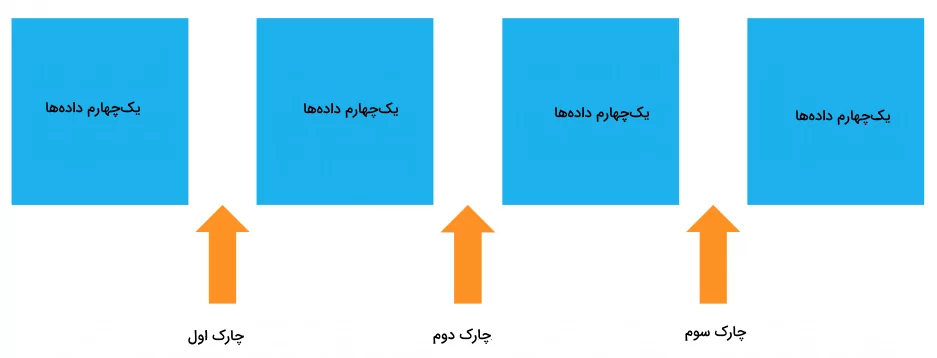
در این بخش میخواهیم با روش دیگری که در مورد توزیعهای احتمال کاربرد دارد، چارکهای اول تا سوم را پیدا کنیم. چارکها نوعی «چندک» (Quantile) یا بهطور دقیقتر، نوعی «صدک» (Percentile) محسوب میشوند. یک صدک مقداری است که درصد مشخصی از دادهها کمتر از آن هستند. بهطور کلی، k درصد از دادهها زیر صدک kام قرار میگیرند. حالا اگر بخواهیم بر این اساس چارکها را تعریف کنیم، خواهیم داشت:
- چارک اول یا چارک پایینتر صدک ۲۵ام است، به این معنا که ۲۵ درصد از دادهها زیر Q۱ قرار میگیرند.
- چارک دوم یا میانه صدک ۵۰ام است، به این معنا که ۵۰ درصد از دادهها زیر Q۲ قرار میگیرند.
- چارک سوم یا چارک بالاتر صدک ۷۵ام است، به این معنا که ۷۵ درصد از دادهها زیر Q۳ قرار میگیرند.
به این ترتیب با شکستن دادهها در صدکهای ۲۵ام، ۵۰ام و ۷۵ام، چارکها دادهها را به چهار بخش مساوی تقسیم میکنند. شکل بالا نمونهای از تقسیم شدن یک توزیع احتمال به چهار بازه با احتمال مساوی توسط چارکها است.
نمایش چارکها با نمودار جعبهای (Boxplot)
در این قسمت نشان میدهیم یکی از راههای نمایش چارک چیست. نمودارهای جعبهای یا باکس پلاتها در ارائه یک تصویر کلی از وضعیت دادهها بسیار سودمند هستند. این نوع نمودار شامل خطوط (Whiskers) و جعبههایی است که خطوط به کمترین و بیشترین تعداد مشاهدات اشاره دارند و جعبهها نشاندهنده چارکها هستند. برای رسم یک نمودار جعبهای اولین کاری که باید بکنید این است که پنج مرحله زیر را انجام دهید:
- پیدا کردن «کمینه» (Minimum) یا min
- پیدا کردن چارک اول
- پیدا کردن چارک دوم
- پیدا کردن چارک سوم
- پیدا کردن «بیشینه» (Maximum) یا max
کمینه یا کمترین مقدار به معنای کمترین مقدار در مشاهدات است. اگر اعدادی که در مجموعه داده خود دارید را از کمترین مقدار به بیشترین مقدار مرتب کنید، کمینه یا مینیمم برابر است با اولین عدد، که به آن چارک صفرم هم میگویند. در سمت مقابل، بیشینه یا ماکزیمم را داریم که برابر است با بیشترین مقدار در مشاهدات و آخرین عدد از مجموعه دادههای مرتب شده را شامل میشود. به همین علت به آن چارک چهارم هم گفته میشود. از هر کدام از این پنج مرحله یک عدد بهدست میآید. با داشتن این ۵ عدد، میتوانید نمودار جعبهای خود را رسم کنید.
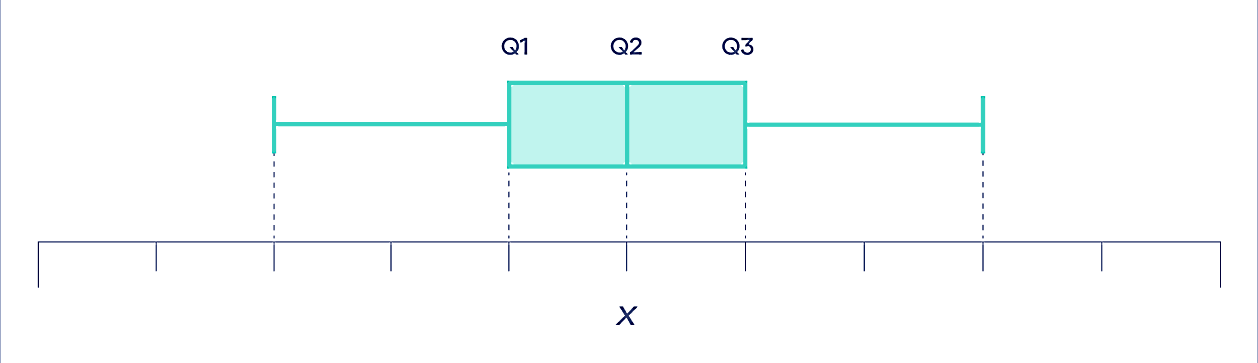
شکل بالا نمونهای از یک باکس پلات را نشان میدهد که در آن چارک اول تا سوم و مقادیر کمینه و بیشینه مشخص شدهاند. روشی که در بالا توضیح دادیم، تنها راه رسم نمودار جعبهای نیست. همانطور که گفتیم، جعبههای یک باکس پلات همیشه نشاندهنده چارکها هستند، اما اغلب خطوط در نقاطی قرار میگیرند که برابر است با ۱٫۵ برابر دامنه میانچارکی از Q۱ تا Q۳. در بخش بعد یک نمونه نمودار جعبهای رسم میشود تا بهتر متوجه تاثیر چارکها در تحلیل دادهها شوید.
مثال رسم نمودار جعبهای
همانطور که در مثال مطالعه پیشرفت زبانآموزی بچهها دیدیم، ۱۴ شرکتکننده دارای سنهای مختلفی بین ۱ تا ۶ سال بودند که به شکل زیر مرتب میشود:
۶ - ۶ - ۵ - ۵ - ۴ - ۳ - ۳ - ۳ - ۳ - ۲ - ۲ - ۲ - ۱ - ۱
نمودار جعبهای این دادهها را رسم کنید:
پاسخ
یاد گرفتیم که برای رسم نمودار جعبهای لازم است پنج مرحله طی شود. مرحله اول پیدا کردن کمینه است. دقت کنید پیش از آن بهتر است حتما دادههای خود را از کمترین به بیشترین مقدار مرتب کرده باشید. پس از چینش دادهها، واضح است که کمترین مقدار یا min برابر است با ۱. حالا میرویم سراغ تعیین چارکها. اگر خاطرتان باشد مقدار سه چارک برای این دادهها در مثال بخش قبل پیدا شد. پس نیازی به تکرار محاسبات نیست. مرحله آخر یافتن بیشینه است که برابر است با عدد ۶. پس میتوانیم پنج عدد خود را به شکل زیر مرتب کنیم:
- کمینه: ۱ سال
- چارک اول: ۲ سال
- چارک دوم: ۳ سال
- چارک سوم: ۵ سال
- بیشینه: ۶ سال
اعداد بالا محل قرارگیری جعبهها و خطوط را روی محور افقی نمودار مشخص میکنند، به این صورت که ابتدا محل اهر عدد صحیح را به ترتیب با شروع از صفر روی محور افقی مشخص میکنیم. برای مقادیری که ما داریم تا عدد ۷ یا ۸ کافی است. سپس بالای عدد ۱ خط کمینه، بالای عدد ۲ خط چارک اول، بالای عدد ۳ خط چارک دوم، بالای عدد ۵ خط چارک سوم و بالای عدد ۶ خط بیشینه را بهصورت عمودی و کوتاه رسم میکنیم. گفتیم چارکها با جعبه نشان داده میشوند، پس با وصل کردن خطوط چارکها جعبه را تکمیل میکنیم و با یک خط افقی، ابتدا و انتهای جعبه را به کمینه و بییشینه متصل میکنیم. در نتیجه، نمودار جعبهای برای این مثال به شکل زیر خواهد شد:
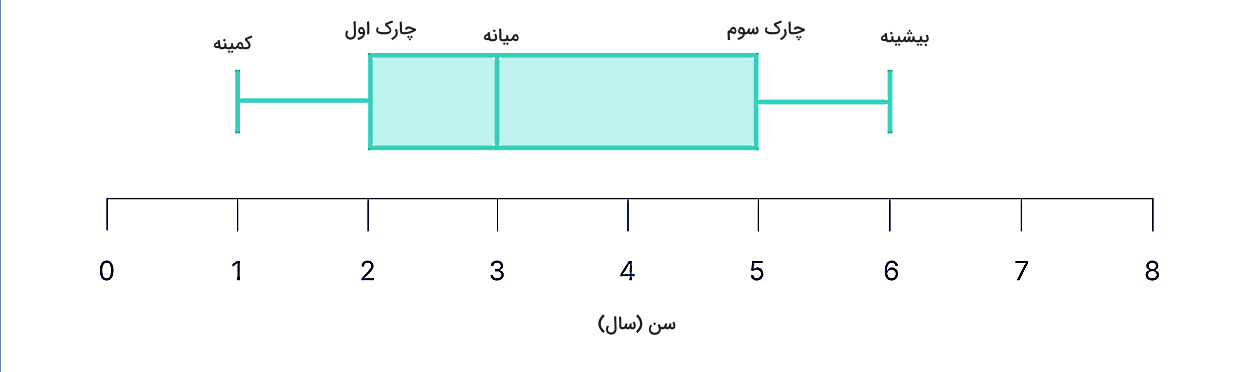
چارکها چه اطلاعاتی به ما میدهند؟
اگر بخواهیم بدانیم هدف از پیدا کردن چارک چیست، پاسخ این است که چارکها اطلاعات مفیدی در مورد یک مشاهده یا یک مجموعه داده به ما میدهند. پس برای کسب اطلاعات بیشتر در مورد بقیه یک نمونه یا جامعه آماری خود، بهتر است وضعیت چارکها را تفسیر کنیم. اطلاعاتی که چارک به ما میدهد، شامل موارد زیر است که در ادامه هر کدام را بهطور مختصر توضیح خواهیم داد:
- مقایسه مشاهدات
- میانه
- دامنه میانچارکی
- خمیدگی یا چولگی
- تشخیص دادههای پرت
مقایسه مشاهدات
یکی از ابتداییترین کاربردهای چارک این است که از مقایسه یک مشاهده با چارکها، میتوان تعیین کرد که برای مثال آیا این مشاهده در فاصله ۲۵٪ اول قرار میگیرد یا در وسط یا در ۲۵٪ آخر.
میانه
اگر خاطرتان باشد، در بخشهای قبل اشاره کردیم که نام دیگر دومین چارک چیست. چارک دوم همان «میانه» (Median) است که برابر است با اندازهای از تمایل مرکزی در دادهها. این عدد میانی، اندازه دقیقی از میانگین یا مرکزیترین مقدار عددی در بین مقادیر دادهها است. محاسبه میانه بخصوص در توزیعهایی که دارای «خمیدگی یا چولگی» (Skewness) هستند یا زمانی که توزیع ما دارای «دادههای پرت» (Outliers) باشد، بسیار مفید است.
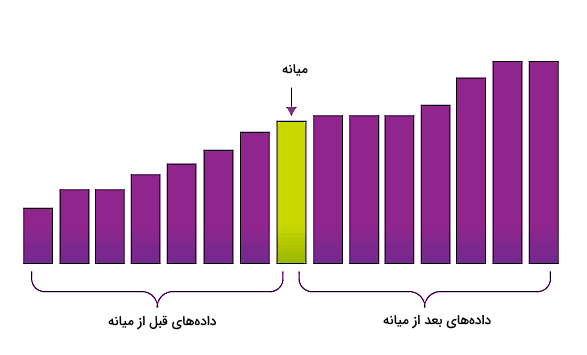
بنابراین یکی از خروجیها در پیدا کردن چارک، تعیین میانه است که میتواند در تحلیل دادههای ما بسیار مفید باشد. البته مقدار میانه به تنهایی نمیتواند به ما اطلاعاتی در مورد نحوه پخش دادهها قبل و بعد میانه بدهد. در واقع این چارکها هستند که نشان میدهند دادههای قبل و بعد از میانه به چه شکلی توزیع شدهاند.
دامنه میانچارکی
در این بخش به معرفی مفهومی میپردازیم که نشان میدهد میزان تغییرپذیری چارک چیست. این مفهوم «دامنه میانچارکی یا دامنه بین چارکی» (Interquartile Range) نام دارد و معمولا با IQR نمایش داده میشود. دامنه میانچارکی، فاصله بین چارک اول تا سوم است و نحوه پخششدگی میانگین ۵۰٪ از دادهها را نمایش میدهد. فرمول محاسبه دامنه میانچارکی بهصورت زیر است:
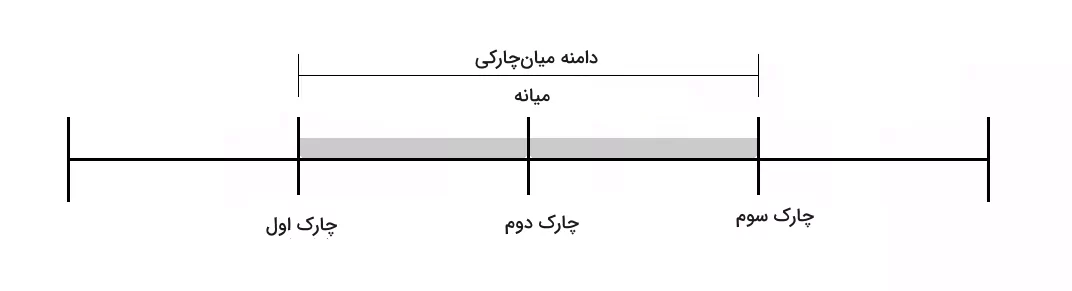
IQR میزان تغییرپذیری در توزیعهای خمیده یا توزیعهایی که دادههای پرت دارند، را بهخوبی نشان میدهد. نکته مهم در مورد این کمیت این است که IQR فقط میانگین ۵۰٪ از دادهها را شامل میشود. بنابراین برخلاف دامنه، IQR تحت تاثیر مقادیر حدی نیست. میدانیم دامنه یا Range برابر است با اختلاف بیشترین و کمترین مقدار، در حالی که تعریف دامنه میانچارکی با فرمول بالا توضیح داده میشود که شامل کمترین یا بیشترین مقدار نیست. بنابراین پس از اینکه توانسیتم چارک اول و چارک سوم را در یک مجموعه داده تعیین کنیم، با محاسبه IQR میتوانیم تغییرپذیری دادههای خود را مشخص کنیم.
خمیدگی یا چولگی
در بخش میانه اشاره کردیم که در مورد توزیعهای دارای چولگی یا خمیدگی، تاثیر محاسبه دومین چارک چیست. اما چطور بفهمیم یک توزیع چولگی دارد؟ پاسخ این است که از فاصله بین چارکها میتوانید متوجه شوید که آیا یک توزیع دارای خمیدگی است یا متقارن است. روش کار به این صورت است که ابتدا باید نمودار جعبهای مربوط به دادههای خود را رسم کنید و سپس به فواصل بین چارکها دقت کنید.

برای مثال در شکل بالا دو نمودار جعبهای را مشاهده میکنید که IQR یا دامنه میانچارکی برابر دارند. پس IQR نمیتواند به ما سرنخی در مورد نحوه خمیدگی این توزیعها بدهد. اما میتوانیم با مقایسه فواصل بین چارکها در هر نمودار، متوجه این مسئله شویم. مثلا در نمودار اول از سمت راست، فاصله بین چارک اول و دوم یا همان میانه از فاصله بین چارک سوم و میانه کمتر است. بنابراین انتظار داریم یک چولگی یا کجی در سمت راست توزیع مربوط به این نمودار قرار داشته باشد. چنین توزیعی را توزیع خمیده مثبت مینامیم.
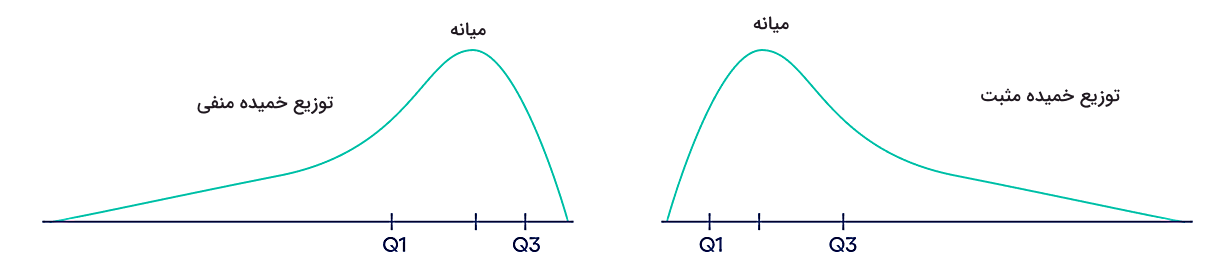
در نمودار جعبهای دوم (سمت چپ)، فاصله بین چارک اول و میانه نسبت به فاصله بین میانه و چارک سوم بیشتر است. پس توزیع مناسب برای این نمودار در سمت چپ خود یک کجی خواهد داشت و آن را توزیع خمیده منفی مینامیم. بهعبارت دیگر، دم یا کشیدگی توزیع منفی در سمت چپ آن قرار دارد. البته باید دقت داشته باشید که بهتر است برای اطمینان بیشتر در مورد نحوه خمیدگی، از روشهایی مانند رسم هیستوگرام یا محاسبه اندازه چولگی استفاده کنید. نکته دیگر در مورد توزیعهای خمیده این است که چون بیشتر مقادیر در یک سمت از توزیع نسبت به مرکز آن قرار میگیرند، سه کمیت میانگین، میانه و مد مقادیر متفاوتی خواهند داشت. پس یکی از نشانههای توزیع دارای چولگی این است.
تشخیص دادههای پرت
در انتها یاد میگیریم که روش تشخیص دادههای پرت با استفاده از چارک چیست. دادههای پرت به مشاهداتی گفته میشود که مقادیر مربوط به آنها خیلی بالا یا خیلی پایین است. یکی از نشانههایی که نشان میدهد با یک داده پرت مواجه هستیم این است که مقدار آن داده نسبت به ۱٫۵ برابر IQR خیلی بیشتر یا کمتر است.
بهطور دقیقتر، هر دادهای که از بیشتر و از کمتر باشد، داده پرت محسوب میشود. بنابراین اگر چارکهای اول و سوم را پیدا کرده باشیم، میتوانیم IQR را محاسبه کنیم و در نتیجه، متوجه شویم که داده موردنظر ما پرت محسوب میشود یا خیر.
مثال مقایسه نمودارهای جعبهای
در این مثال قصد داریم نشان دهیم چگونه با استفاده از تعیین چارکها و سپس رسم نمودار جعبهای، میتوان اطلاعاتی بهدست آورد که برای مقایسه عملکرد مفید هستند. پس به نوعی یاد میگیریم یکی از سادهترین کاربردهای چارک چیست. فرض کنید یک آزمون ریاضی مشترک بین دو کلاس A و B برگزار شده است و دو نمودار جعبهای زیر نتایج آن را برای هر کلاس نشان میدهد:
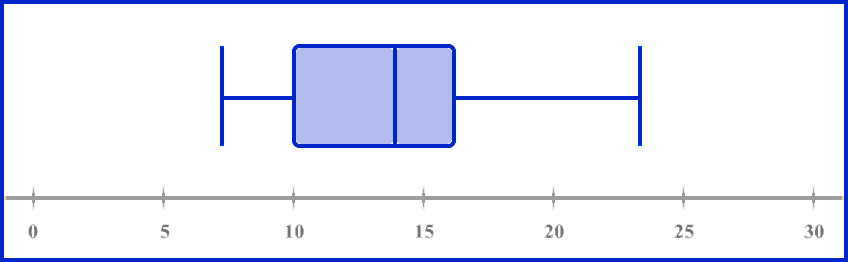
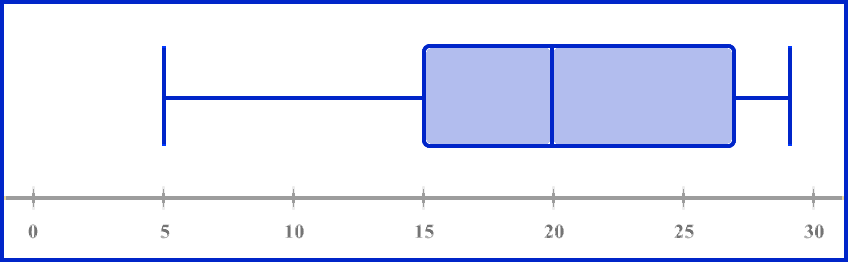
با توجه به نمودارهای بالا، پیشرفت دو کلاس را با هم مقایسه کنید:
پاسخ
یکی از راههای مقایسه عملکرد دو کلاس، بررسی میانه است. میانه در نمودار جعبهای معادل است با خط داخل جعبه. پس در نمودار کلاس A مقدار میانه برابر است با ۱۴ در حالی که برای کلاس B، میانه برابر با ۲۰ است. همین جا میتوانیم نتیجهگیری کنیم که بطور میانگین، عملکرد کلاس B از کلاس A بهتر بوده است.
راه دیگر مقایسه، بررسی دامنه میانچارکی یا IQR است. برای پیدا کردن IQR از روی نمودار جعبهای کافی است مقادیر متناظر با ابتدا و انتهای جعبه را از هم کم کنیم. برای کلاس A مقدار دامنه میانچارکی برابر است با:
در حالی که برای کلاس B خواهیم داشت:
کمتر شدن IQR برای کلاس A به این معنا است که این کلاس عملکرد یکدستتری دارد یا یادگیری دانشآموزان این کلاس بیشتر شبیه هم است. اما نمرات کلاس B دارای پراکندگی بیشتری است و این نشان میدهد که یادگیری در این کلاس در سطوح مختلفی است.
پیدا کردن چارک با اکسل
یکی از بهترین نرمافزارها برای انجام محاسبات آماری، نرمافزار اکسل است. در این بخش با یک مثال نشان میدهیم که در اکسل روش پیدا کردن چارک چیست. فرض کنید نمرات ریاضی کلاسی با ۱۹ دانشآموز به شرح زیر است:
۹۵ - ۹۰- ۸۷ - ۸۴ - ۸۲ - ۸۱- ۷۷ - ۷۶ - ۷۵ - ۷۵ - ۷۲ - ۷۰ - ۶۹ - ۶۸ - ۶۵ - ۶۵ - ۶۰ - ۵۹
اولین قدم این است که این دادهها را در یک ردیف اکسل یا در یک ستون آن وارد کنید. فرض کنید طبق شکل زیر دادهها را در ردیف ۲ به شکل زیر وارد کردهاید. اگر دقت کنید نیازی به مرتب کردن دادهها نیست، چون به ترتیب از کمترین مقدار تا بیشترین مقدار نوشته شدهاند.
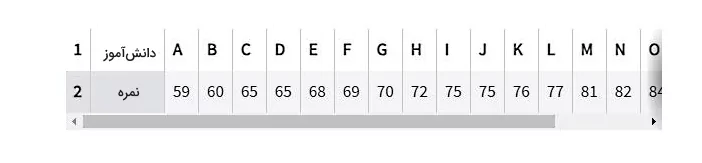
برای یافتن چارکها در اکسل میتوانید خیلی راحت از توابعی که با همین هدف طراحی شدهاند، استفاده کنید. در استفاده از این توابع باید دقت کنید که متغیر دوم در تابع، نشاندهنده چارکی است که میخواهید آن را محاسبه کنید:
اگر دستورات را بهدرستی وارد کنید، چارک اول تا سوم بهصورت زیر بهدست میآیند:
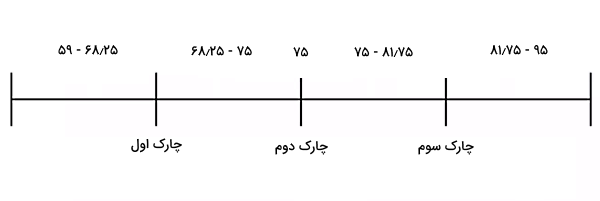
محاسبه چارک در دادههای گروهی
در بخشهای قبل آموختیم که چگونه میتوان چارک را در مورد یک مجموعه داده پیدا کرد. اگر دقت کنید دادههایی که در بخشهای قبل داشتیم دارای مقادیر مشخص بودند. اما گاهی ممکن است «دادههای گروهی» (Grouped Data) در اختیار ما قرار داده شوند، به این صورت که دادهها شامل چند بازه باشند. در ادامه خواهیم دید برای چنین دادههایی چارک چیست.
برای نمونه دادهای مربوط به قد ۴۰ دانشآموز را در نظر بگیرید که بهصورت جدول زیر داده شده است.
| قد یا h (متر) | فراوانی |
قصد داریم بررسی کنیم که چارک بالا و پایین در کدام بازه قدی قرار میگیرند. برای شروع، لازم است دادهها شمارش شوند تا مقدار n مشخص شود. با توجه به مقادیر فراوانی، n = ۴۰ است. در صورت سوال هم این نکته ذکر شده است که دادهها مربوط به قد ۴۰ دانشآموز است. مرحله بعدی این است که از فرمول مربوط به چارک اول استفاده کنیم تا Q۱ محاسبه شود. طبق این فرمول داریم:
عدد ۱۰ یک عدد صحیح است، پس چارک اول با محاسبه میانگین اعدادی که در موقعیتهای دهم و یازدهم قرار دارند، بهدست میآید. حالا چطور بفهمیم موقعیت دهم و یازدهم در کدام بازه قرار دارند؟ در اینجا لازم است از مفهومی به نام «فراوانی تجمعی» (Cumulative Frequency) استفاده کنیم که در بخش بعد آن را توضیح دادهایم.
| قد یا h (متر) | فراوانی | فراوانی تجمعی |
پس از اینکه فراوانی تجمعی را برای هر بازه محاسبه کردیم، متوجه خواهیم شد که طبق محاسبات ۱۵ عدد داده داریم که مقادیری کمتر از ۱٫۶ دارند (ردیف سوم جدول بالا). پس دادههای دهم و یازدهم حتما در این بازه قرار دارند. نتیجهگیری این است که چارک اول در گروه یا بازه قرار دارد.
برای یافتن چارک سوم از فرمول استفاده میکنیم:
عدد صحیح ۳۰ حاصل شد. پس باید بدانیم اعدادی که در موقعیتهای ۳۰ و ۳۱ قرار دارند، چه هستند. باز به جدول بالا و ستون فراوانی تجمعی نگاه میکنیم تا ببینیم در کدام بازه مقدار فراوانی تجمعی شامل این اعداد میشود. ۳۶ عدد داده داریم که دارای مقادیر کمتر از ۱٫۸ هستند. پس چارک سوم در این بازه یعنی قرار دارد.
روش محاسبه فراوانی تجمعی
برای اینکه بتوانیم تشخیص دهیم در مورد دادههای گروهی چارک چیست و چگونه بهدست میآید، لازم است ابتدا با فرمول محاسبه فراوانی تجمعی آشنا شویم. فراوانی یا فراوانی مطلق به معنای تعداد دفعاتی است که یک مقدار مشخص در یک مجموعه داده ظاهر میشود، در حالی که فراوانی تجمعی مجموع تمام فراوانیهای بالاتر از یک نقطه خاص در یک مجموعه داده را به شما میدهد.

از طرفی دادههای ما ممکن است گسسته یا پیوسته باشند. معمولا دادههای پیوسته را به شکل بازههایی از مقادیر بیان میکنند که مهم است این بازهها یا فواصل با هم برابر باشند. اما اینکه چند مقدار در هر بازه قرار بگیرد، اهمیتی ندارد. در ادامه این بخش روش محاسبه فراوانی تجمعی را توضیح میدهیم که شامل مراحل زیر است:
- مرحله اول: مرتب کردن دادهها
- مرحله دوم: شمارش فراوانی
- مرحله سوم: یافتن فراوانی تجمعی اولین مقدار
- مرحله چهارم: یافتن فراوانی تجمعی مقدار بعدی
- مرحله پنجم: تکرار مرحله قبل برای بقیه مقادیر
- مرحله ششم: چک درستی
- فراوانی تجمعی در دادههای گروهی
مرحله اول: مرتب کردن دادهها
فرض کنید چند عدد را بهعنوان دادههای خود دارید. اولین قدم این است که این دادهها را از کمترین مقدار به بیشترین مقدار به شکل زیر مرتب کنید.
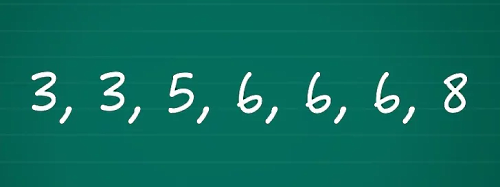
مرحله دوم: شمارش فراوانی
در قدم بعدی اعدادی که تکرار شدهاند را با عنوان فراوانی در ستون دیگری درج کنید. برای مثال دو تا عدد ۳ داریم، پس فراوانی عدد ۳ برابر است با ۲.
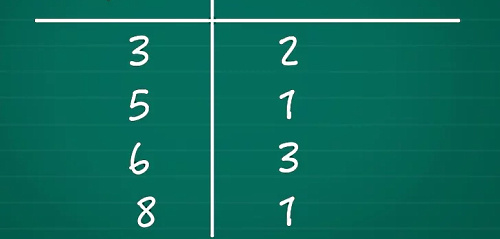
مرحله سوم: یافتن فراوانی تجمعی اولین مقدار
دقت کنید باید از کمترین مقدار که همان اولین مقدار در دادههای مرتب شده است، شروع کنید که در اینجا میشود عدد ۳. فراوانی این عدد برابر است با ۲. پس فراوانی تجمعی هم برابر میشود با ۲.
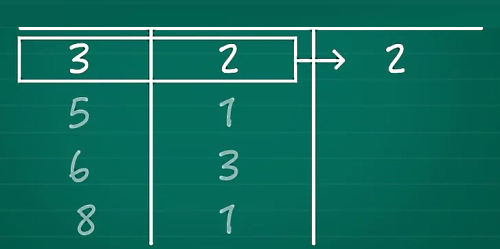
مرحله چهارم: یافتن فراوانی تجمعی مقدار بعدی
حالا میرویم سراغ یافتن فراوانی تجمعی برای مقدار بعدی. تا الان نشان دادیم که کمترین مقدار چند بار در دادهها ظاهر میشود. برای یافتن فراوانی تجمعی مقدار بعدی، کافی است فراوانی تجمعی داده قبلی را با فراوانی مطلق داده جدید جمع کنید.
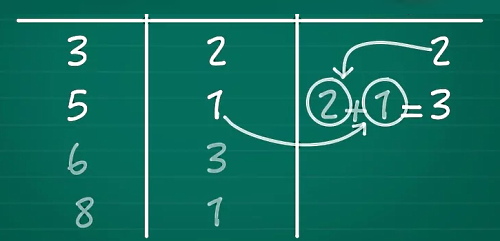
مرحله پنجم: تکرار مرحله قبل برای بقیه مقادیر
در انتها همین روند را برای هر داده تکرار میکنیم، به این ترتیب که فراوانی تجمعی هر داده برابر است با مجموع فراوانی مطلق همان داده با فراوانی تجمعی داده قبل آن.

مرحله ششم: چک درستی
برای اینکه مطمئن شویم محاسباتمان درست بوده است، یکی از راهها این است که تمام فراوانیهای مطلق را با هم جمع کنیم. حاصل باید با آخرین فراوانی تجمعی برابر باشد. در مورد دادهها ما، مجموع فراوانیهای مطلق برابر است با ۷ که همان آخرین فراوانی تجمعی است. یک روش دیگر هم این است که دادهها را کامل بنویسیم و بشمریم که چند عدد داده داریم. عدد حاصل همان آخرین فراوانی تجمعی است.
فراوانی تجمعی در دادههای گروهی
در مورد دادههای گروهی دانستن مفهوم فراوانی تجمعی و نحوه محاسبه آن برای اینکه بدانیم چارک چیست، مهمتر میشود. فرض کنید چند داده به شکل زیر داریم که میخواهیم آنها را به شکل دادههای گروهی در جدولی مرتب کنیم. سه بازه با فواصل برابر ۵۰۰، برای این دادهها در نظر میگیریم و فراوانی مطلق و فراوانی تجمعی را طبق آنچه در بخش قبل گفتیم محاسبه میکنیم.
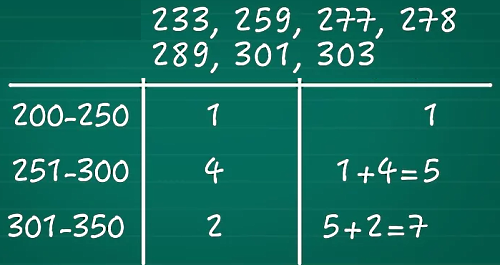
چندک چیست؟
در این بخش میخواهیم ببینیم بهعنوان یک نوع چندک، تعریف چارک چیست. پس اول باید تعریف چندک را بدانیم. چندکها مقادیری هستند که دادههای مرتب شده یا یک توزیع احتمال را به بخشهای مساوی تقسیم میکنند. به طور کلی یک q-چندک، دادههای مرتب شده ما را به q بخش مساوی تقسیم میکند. چندکهایی که در آمار زیاد استفاده میشوند، عبارتاند از:
- چارکها (۴-چندک): متشکل است از سه چارک که دادهها را به چهار بخش تقسیم میکنند.
- «دهکها» (Deciles) (۱۰-چندک): متشکل است از نه دهک که دادهها را به ده بخش تقسیم میکنند.
- «صدکها» (Percentiles) (۱۰۰-چندک): متشکل است از ۹۹ صدک که دادهها را به صد بخش تقسیم میکنند.

همانطور که قبلا گفتیم، بین چارک و صدک ارتباط نزدیکی وجود دارد، به این صورت که هر چارک ۲۵٪ یا یک چهارم از دادهها را جدا میکند. بسته به اینکه چه نوع چندکی داشته باشیم، همیشه تعداد چندکها از تعداد اجزایی که پس از تقسیم شدن دادهها بهدست میآیند، یک واحد کمتر است. مثلا در مورد چارک، دادهها به ۴ بخش تقسیم میشوند، در حالی که ۳ نوع چارک بکار میرود. روش یافتن چندکها دقیقا مشابه روشی است که برای پیدا کردن چارک استفاده کردیم. فقط لازم است برای مثال برای یافتن q-چندک، در مراحل ۳ تا ۵ به جای ضرب کردن n در ۱/۴، آن را در ۱/q ضرب کنیم.
برای نمونه، فرض کنید میخواهیم سومین ۵-چندک را پیدا کنیم، در حالی که n داده داریم. اگر خاطرتان باشد برای یافتن سومین چارک، از فرمول استفاده کردیم. در مورد چارک، مخرج فرمول برابر با عدد ۴ است. اما در اینجا برای ۵-چندک، مخرج فرمول برابر با ۵ خواهد شد و چون سومین ۵-چندک را میخواهیم، صورت کسر همان عدد ۵ است. بنابراین فرمول محاسبه سومین ۵-چندک میشود:
- اگر حاصل یک عدد صحیح شود، در این صورت سومین ۵-چندک برابر است با میانگین اعداد در موقعیتهای و .
- اگر حاصل یک عدد صحیح نشود، در این صورت این عدد باید به سمت بالا گرد شود. حاصل نشاندهنده شماره جایگاه یا موقعیتی است که سومین ۵-چندک در آن قرار دارد.
مثال محاسبه چندک
در یک مغازه خواروبار فروشی، ۱۰ نوع غلات وجود دارد. اگر قیمت این غلات به دلار به شکل زیر باشد، دومین ۳-چندک قیمتها چقدر است؟
۵٫۲۵ - ۳ - ۳٫۱ - ۲٫۹۹ - ۲٫۵ - ۳٫۲۵ - ۳٫۵ - ۳٫۴ - ۳٫۹۹ - ۴
پاسخ
در این سوال چارک خواسته نشده است، بلکه دومین ۳-چندک را باید پیدا کنیم. گفتیم روند کار با پیدا کردن دومین چارک فرقی ندارد. فقط کافی است مخرج فرمول دومین چارک () را از ۴ به ۳ تغییر دهیم. پس فرمول میشود:
n برابر است با ۱۰. پس خواهیم داشت:
گرد شده حاصل بالا برابر است با عدد ۷. پس از مرتب کردن دادهها هفتمین جایگاه یعنی عدد ۳٫۵ برابر خواهد شد با دومین ۳-چندک:
۵٫۲۵ - ۴ - ۳٫۹۹ - ۳٫۵ - ۳٫۴ - ۳٫۲۵ - ۳٫۱ - ۳ - ۲٫۹۹ - ۲٫۵
مسیر یادگیری کاربردهای آمار و احتمال با فرادرس
پس از اینکه توضیح دادیم چارک چیست و چگونه محاسبه میشود، تا حدودی با کاربردهای آن در مواردی مانند تشخیص میزان پراکندگی دادهها و چولگی توزیع آشنا شدیم. اگر تمایل دارید در زمینه کاربرد مفاهیم آمار و احتمال از جمله چارک، اطلاعات خود را گسترش دهید و به تسلط خوبی در این زمینه دست پیدا کنید، پیشنهاد ما این است که از مجموعه فیلمهای آموزشی تهیه شده در فرادرس استفاده کنید.

در ادامه پس از معرفی چند آموزش دانشگاهی پایهای آمار و احتمال، برخی از کاربردیترین دورههای فرادرس را به شما معرفی کردهایم که در آنها از مفاهیم آماری در زمینه یادگیری ماشین یا مدیریت و علوم انسانی استفاده شده است:
- فیلم آموزش آمار و احتمال مهندسی جامع و با مثال های مختلف فرادرس
- فیلم آموزش مبانی احتمال مرور و حل تست کنکور ارشد فرادرس
- فیلم آموزش آمار و کاربرد آن در مدیریت ۱ فرادرس
- فیلم آموزش رایگان درخت تصمیم در یادگیری ماشین فرادرس
- فیلم آموزش رایگان رگرسیون لجستیک در یادگیری ماشین فرادرس
- فیلم آموزش رایگان انواع داده در کامپیوتر فرادرس
- فیلم آموزش یادگیری ماشین و پیاده سازی در پایتون Python بخش یکم فرادرس
به علاوه، میتوانید فیلم آموزشی نحوه کار با نرمافزارهای آماری مانند SPSS را نیز مشاهده کنید. همچنین میتوانید از فیلمهایی که جهت شرکت در آزمونهای مختلف برای شما تهیه شده است نیز استفاده کنید:
- فیلم آموزش رایگان تابع Frequency در اکسل برای محاسبه فراوانی فرادرس
- فیلم آموزش محاسبات آماری در اکسل Excel فرادرس
- مجموعه آموزش اس پی اس اس SPSS – مقدماتی تا پیشرفته فرادرس
- فیلم آموزش آمار مرور و حل سوالات آزمون های استخدامی فرادرس
جمعبندی
در این نوشته از مجله فرادرس یاد گرفتیم چارک چیست و چگونه محاسبه میشود. چارک یکی از مفاهیم آمار توصیفی است که تقسیمبندی مشاهدات به چهار گروه با فواصل تعریف شده را برای ما ممکن میسازد. سه نوع چارک داریم که چارک اول یا پایین، چارک دوم یا میانه و چارک سوم یا بالا نام دارند.

پیدا کردن چارکها به این صورت است که اگر دادهها را به ترتیب از کمترین مقدار تا بیشترین مقدار مرتب کنیم، میتوانیم چهار گروه ۲۵٪ای با فواصل برابر بسازیم که توسط سه عدد از هم جدا شدهاند و این سه عدد همان چارکهای اول تا سوم هستند. سه نوع چارک بین کمترین و بیشترین مقدار عددی در دادهها قرار میگیرند. یکی از بهترین راههای نمایش چارکها به همراه این کمترین و بیشترین مقادیر، رسم نمودار جعبهای دادهها است که در آن جعبهها نشاندهنده چارک و خطوط بیانگر مقادیر کمینه و بیشینه هستند.













خیلی عالی نوشته اید ممنون
سپاس.کامل و ساده و مفصل
خیلی جامع و کامل توضیح داده شد
ممنون ازتون.