نیروی کشش چیست؟ – انواع، ویژگی و محاسبه به زبان ساده
به طور حتم در دوران کودکی در مسابقه طنابکشی شرکت کردهاید. هنگام مسابقه تمام تلاشتان را میکردید که طناب را با قدرت هر چه تمامتر بکشید تا برنده شوید. یا شاید در کودکی با وسیلهای به نام یویو بازی کردهاید. شاید در اخبار روزمره خبر سقوط آسانسور در ساختمان یا ادارهای را شنیده باشید. طناب نقطه اشتراک مسابقه طنابکشی، اسبابباری یویو و آسانسور است. در این مطلب با تعریف نیروی کشش آشنا میشوید و در پایان میتوانید به پرسش نیروی کشش چیست پاسخ دهید.

نیروی کشش چیست ؟
تمام اجسام فیزیکی که در تماس با یکدیگر قرار دارند بر هم نیرو وارد میکنند. با توجه به نوع اجسام، نامهای گوناگونی برای این نیروهای تماسی انتخاب میکنیم. اگر یکی از اجسامی که نیرو وارد میکند طناب، نخ، زنجیر، یا کابل باشد به این نیرو، «نیروی کششی» (Tension Force) میگوییم.
ریشه کلمه «Tension» از عبارتی لاتین به معنای کشیدن میآید. طنابهای انعطافپذیری که نیروهای ماهیچهای را به قسمتهای دیگر بدن منتقل میکنند، تاندون نامیده میشوند. هر اتصالدهنده انعطافپذیری مانند نخ، طناب، زنجیر، سیم یا کابل نیروی کششی در راستای طولش وارد میکند.
طناب چگونه نیرو وارد می کند ؟
اگر جسمی را با استفاده از طنابی بکشید، طناب کشیده خواهد شد (اغلب به طور نامحسوس). این کش آمدن طناب، سبب کشش طناب خواهد شد. در نتیجه این کش آمدن، نیرو از قسمتی از طناب به قسمت دیگر منتقل میشود. این انتقال نیرو شبیه نیروی وارد شده از طرف فنر کشیده شده بر اجسام متصل به آن است. کش آمدن طناب به اندازهای کوچک است که در بیشتر مواقع از آن چشمپوشی میشود. اما اگر نیروهای وارد شده بسیار بزرگ باشند، ممکن است طناب یا کابل پاره شود. بنابراین، قبل از استفاده از طنابها، حد یا نهایت کشش آنها را بررسی کنید.
طنابها و کابلها برای وارد کردن نیروها به اجسام مختلف مفید هستند. زیرا آنها قادر به انتقال نیرو در فاصله زیاد خواهند بود (در حدود طول طناب). باید به این نکته توجه کنیم که نیروی کشش، نیروی کشیدن است. طنابها یا کابلها نمیتوانند به طور موثر نیروی فشاری بر جسمی وارد کنند. اگر تلاش کنیم به وسیله طناب بر جسمی فشار وارد کنیم، طناب نه تنها خاصیت کشش خود را از دست میدهد بلکه شل نیز خواهد شد. شاید عبارت گفته شده در نگاه اول واضح به نظر برسد اما به هنگام رسم نیروهای وارد بر جسم، در بیشتر موارد جهت نیروی کشش را اشتباه رسم میکنیم. باید به یاد داشته باشیم که نیروی کششی تنها میتواند جسم را بکشد.
نیروی کشش سطحی چیست ؟
به مقاومت سطح مایع در برابر از همگسیختگی به هنگام اعمال نیروی کششی یا تنشی، کشش سطحی میگویند.
ممکن است نشستن سنجاقکی بر روی سطح آب را دیده باشید. آیا تاکنون به محلی که سنجاقک نشسته است توجه کردهاید؟ اگر به سطح آب دقت کنید شبیه پارچه کشیده شدهای رفتار میکند.

مولکولهای آب یکدیگر را جذب میکنند. این نیروی جاذبه سبب تشکیل قطره آب میشود. دلیل کروی بودن قطرههای آب آن است که آنها میخواهند در فاصله بسیار نزدیکی از یکدیگر قرار داشته باشند. آیا تاکنون لیوانی را تا لبه از آب پر کردهاید؟ این کار انجام دهید. سپس، چند قطره آب را بسیار آهسته به آن اضافه کنید. قبل از آنکه آب از لیوان سرریز شود، به شکل گنبد در میآید. این شکل گنبدمانند به دلیل خاصیت چسبندگی مولکولهای آب یا نیروی جاذبه بین آنها، تشکیل میشود. به جذب شدن مولکولهای یکسان (مانند مولکولهای آب) به یکدیگر چسبندگی میگوییم. آب، نیروهای چسبدگی بسیار قوی دارد.
نیروهای چسبندگی مسئول کشش سطحی هستند. مولکولهای آب در سطح آن (مرز هوا و آب) با مولکولهای همسایه تشکیل پیوند هیدروژنی میدهند. اما از آنجایی که در سطح آب، مولکولهای آب کمتری وجود دارند، بنابراین تعداد مولکولهای همسایه نیز کمتر خواهد بود. در نتیجه، مولکولهای آب با مولکولهای همسایه پیوندهای قویتری تشکیل میدهند. دلیل شکل کروی قطرههای آب، کشش سطحی است.
واحد کشش سطحی نیرو بر واحد طول یا انرژی بر واحد سطح است. این دو واحد معادل هستند، اما هنگامی که از انرژی بر واحد سطح استفاده میکنیم، عبارت انرژی سطحی رایجتر خواهد بود.
کاربرد های کشش سطحی در زندگی روزمره
یکی از کاربردهای مهم نیروی کشش سطحی در مایعات به خصوص آب است.
قطره آب
به هنگام بارش باران، قطرات آب بر روی سطوح مومی مانند برگ تشکیل میشوند. چسبندگی قطرههای آب به این سطح ضعیف، اما به یکدیگر بسیار قوی است. قطرههای کوچکتر آب با اتصال به یکدیگر قطرههای بزرگتر را تشکیل میدهند. قطره آب به دلیل نیروی کشش سطحی شکل کروی دارد. دلیل این امر آن است که کره، کمترین نسبت سطح به حجم را دارد.
غوطه ور شدن روی سطح آب
اجسام چگالتر از آب تا هنگامی که وزن بسیار پایینی دارند بر روی سطح آب شناور میمانند. وزن آنها به اندازهای است که توسط نیروهای کشش سطحی قابل تحمل باشند. به عنوان مثال، سنجاقکها با استفاده از کشش سطحی بر روی سطح آب راه میروند. رفتار سطح آب مانند، لایهای کشسان است. پای سنجاقک فرورفتگی بر سطح آب ایجاد میکند و سبب افزایش سطح آن میشود.

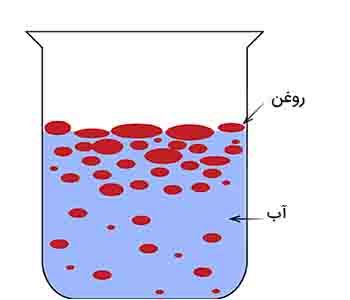
جدایی روغن و آب
جدایی آب و روغن به دلیل نیروی کشش سطحی در سطح بین مایعهای غیر مشابه است. به این نوع کشش سطحی، کشش مرزی میگوییم.
نیروی کشش نخ چیست ؟
اگر جسمی به نخ بدون جرمی متصل شده باشد، از طرف نخ نیروی کششی بر آن وارد میشود. راستای این نیرو، موازی نخ خواهد بود. حالت کلیتر نخ، طناب است که برای آن دو حالت طناب بدون جرم و طناب جرمدار را در نظر میگیریم.
نیروی کشش را چگونه به دست می آوریم ؟
فرمول یا رابطه خاصی برای به دست آوردن نیروی کشش وجود ندارد. نحوه به دست آوردن نیروی کشش مانند به دست آوردن نیروی عمودی سطح است. با استفاده از قانون دوم نیوتن حرکت جسم را به نیروهای وارد شده بر آن ربط میدهیم.
- نیروهای وارد شده بر جسم را رسم میکنیم.
- قانون دوم نیوتن را در جهت نیروی کشش مینویسیم.
- با استفاده از رابطه بین شتاب و نیرو در قانون دوم نیوتن، نیروی کشش را به دست میآوریم.
بر طبق قانون دوم نیوتن، نیروهای وارد شده بر جسم برابر حاصلضرب جرم جسم در شتاب حرکت آن است.
مثال اول نیروی کشش طناب
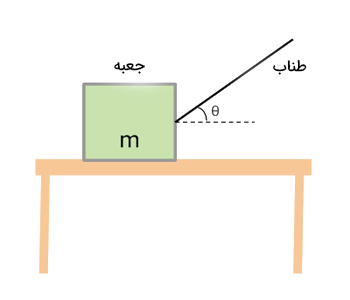
جعبهای به جرم دو کیلوگرم به وسیله طناب بدون جرمی با زاویه ۶۰ درجه نسبت به افق بر روی میز بدون اصطکاکی کشیده میشود. کشش طناب سبب حرکت جعبه بر روی میز با شتاب ۳ متر بر مجذور ثانیه خواهد شد. کشش طناب را به دست آورید.
پاسخ
در ابتدا تمام نیروهای وارد شده بر جعبه را رسم میکنیم (نمودار جسم آزاد). در ادامه، از قانون دوم نیوتن استفاده میکنیم. جهت نیروی کشش هم عمودی و هم افقی است. بنابراین باید در انتخاب جهت درست نیروی کشش دقت کنیم. اما، جهت شتاب حرکت جعبه به کدام سمت است؟ جعبه در راستای افق و به سمت راست حرکت میکند. بنابراین، شتاب حرکت افقی و جهت آن به سمت راست خواهد بود. در نتیجه، از قانون دوم نیوتن در راستای افقی استفاده میکنیم.
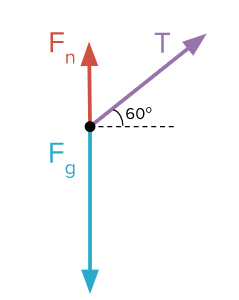
برای قانون دوم نیوتن در راستای افقی داریم:
تنها نیروی وارد شده در راستای افقی، مولفه x نیروی کشش طناب است.
مثال دوم نیروی کشش طناب
جعبهای به جرم ۰/۲۵ کیلوگرم به وسیله دو طناب از سقف آویزان شده است. طناب اول در حالت افقی قرار دارد و طناب دوم با افق زاویه ۳۰ درجه ساخته است. نیروهای کشش در طناب را به دست آورید.
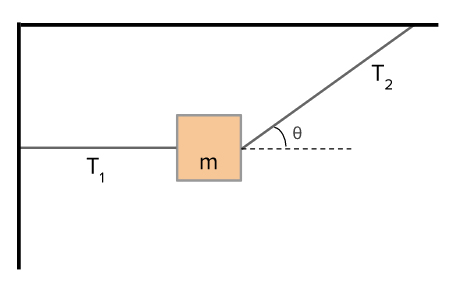
پاسخ
در ابتدا تمام نیروهای وارد شده بر جعبه را رسم میکنیم.
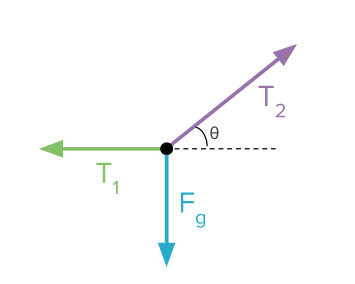
در ادامه از قانون دوم نیوتن استفاده میکنیم. جهت نیروهای کشش هم در راستای عمودی و هم در راستای افقی است. اما وزن جعبه را میدانیم. در نتیجه، ابتدا قانون دوم نیوتن را در راستای عمودی مینویسیم.
با قرار دادن نیروهای عمودی، شتاب عمودی و جرم در رابطه بالا داریم:
ذکر این نکته مهم است که شتاب حرکت جعبه برابر صفر است.
اکنون با دانستن نیروی کشش در طناب دوم، نیروی کشش در طناب اول را به دست میآوریم:
با جایگذاری شتاب افقی، جرم و نیروهای افقی در رابطه بالا داریم:
مثال سوم نیروی کشش طناب
شاید در تلویزیون یا به صورت زنده راه رفتن فردی بر روی طناب را دیده باشید. اکنون میخواهیم نیروی کشش طناب بسته شده را به دست آوریم. برای به دست آوردن نیروی کشش طناب فرض کنید فردی به جرم ۷۰ کیلوگرم بر روی آن ایستاده است و سعی در حفط تعادل خود دارد.
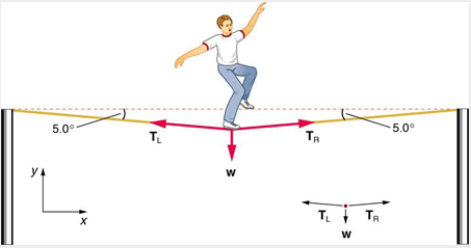
پاسخ
همانگونه که در تصویر فوق مشاهده میکنید، طناب در حالت افقی قرار ندارد و تحت تاثیر وزن فرد، کمی خمیده شده است. بنابراین، نیروی کشش در دو طرف فرد، مولفه عمودی به سمت بالا و در راستای مثبت محور y دارد. سیستم مورد نظر، شخص بر روی طناب است و تنها نیروهای وارد بر او، نیروی وزن و دو نیروی کشش طناب یعنی (کشش از طرف سمت چپ طناب) و (کشش از طرف سمت راست طناب) هستند. در این مثال، از جرم طناب چشمپوشی میکنیم. همچنین، از آنجایی که شخص بر روی طناب در حال تعادل ایستاده است، جمع نیروهای خارجی وارد بر او برابر صفر است. با استفاده از کمی مثلثات نیروهای کشش طناب را پیدا میکنیم.
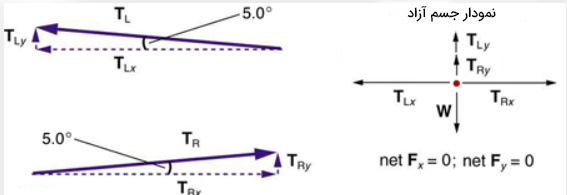
همانگونه که گفتیم چون شخص در حال تعادل قرار دارد، بنابراین برآیند نیروهای وارد بر او در راستای x و y برابر صفر است. در نتیجه، نیروهای کشش و باید با یکدیگر برابر باشند.
برآیند نیروهای وارد بر شخص در راستای x برابر است با:
برآیند نیروهای وارد شده بر شخص در راستای x برابر صفر است، در نتیجه داریم:
اکنون با استفاده از مثلثات، مقدارهای و را به دست میآوریم:
با مساوی قرار دادن و داریم:
اکنون با در نظر گرفتن مولفههای عمودی نیرو، مقدار T را به دست میآوریم.
با استفاده از مثلثات بسیار ساده، رابطه بین و و T را به دست میآوریم:
اکنون مقدارهای و را در رابطه برآیند نیرو در راستای y قرار میدهیم:
در نتیجه مقدار T به صورت زیر به دست میآید:
نیروی کشش طناب جرم دار
تاکنون مثالهایی در مورد نیروی کشش نخ یا طناب بدون جرم حل کردیم. اما در دنیای واقعی، طنابها جرم دارند. بنابراین، در حل مسائل مربوط به نیروی کشش طناب، باید جرم آن را در نظر بگیریم.
مثال اول نیروی کشش طناب جرم دار
جعبهای به جرم بر روی سطح افقی قرار دارد. ضریب اصطکاک جنبشی بین سطح و جعبه برابر است. طناب یکنواختی به جرم و طول d به جعبه وصل شده است. طناب از سمت سر آزاد با نیرویی به بزرگی کشیده میشود. از آنجایی که طناب جرم دارد، نیروی وارد شده بر آن با افق زاویه خواهد ساخت. در این صورت، مولفه عمودی نیروی وارد شده بر طناب با وزن آن برابر و طناب در راستای عمودی حرکتی نخواهد داشت. نیروی کشش طناب را بر حسب تابعی از x به دست آورید. x فاصله از جعبه است.

پاسخ
برای حل این مثال فرض میکنیم که زاویه بسیار کوچک است. در نتیجه، نیروهای کشش طناب و در راستای افقی قرار میگیرند. ذکر این نکته مهم است که در حالت واقعی، برای برقراری تعادل در راستای عمودی، زاویه صفر نخواهد بود.
در این مثال، طناب جرم دارد. در نتیجه، به هنگام نوشتن قانون دوم نیوتن باید این نکته را در نظر بگیریم. بخشی از طناب به فاصله x از جعبه را در نظر میگیریم. طناب به دو قسمت تقسیم میشود. سمت راست آن با طول d-x دارای جرم است. همچنین جرم سمت چپ با طول x، مقدار است.
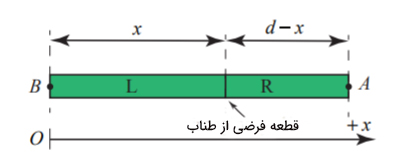
اکنون نمودار جسم آزاد را برای دو قسمت طناب رسم میکنیم. T(x) نیروی کشش طناب در فاصله x از جعبه است. همچنین، بر قسمت سمت چپ طناب نیروی وارد میشود. این نیرو به دلیل برهمکنش طناب و جعبه است.
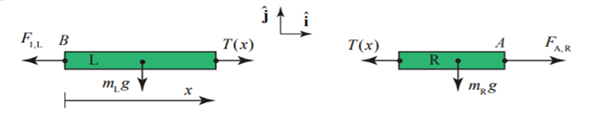
قانون دوم نیوتن را برای سمت راست طناب مینویسیم:
رابطه (۱)
در رابطه بالا برابر مولفه x شتاب سمت راست طناب است. اکنون قانون دوم نیوتن را برای سمت چپ طناب مینویسیم:
رابطه (۲)
در رابطه فوق برابر مولفه x شتاب سمت چپ طناب است. نمودار جسم آزاد برای جعبه در تصویر زیر نشان داده شده است:
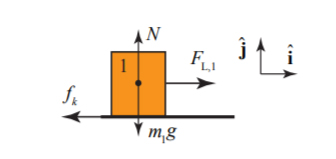
اکنون قانون دوم نیوتن را در راستای محورهای x و y برای جعبه مینویسیم:
مقدار نیروی اصطکاک جنبشی وارد شده بر جعبه، به صورت زیر به دست میآید:
با جایگزینی رابطه اصطکاک جنبشی در قانون دوم نیوتن در راستای مثبت محور x داریم:
بر طبق قانون سوم نیوتن برای برهمکنش جعبه و طناب داریم:
در نتیجه رابطه (۲) به صورت زیر نوشته میشود:
از آنجایی که جعبه و طناب با یکدیگر حرکت میکنند، شتابهای هر دو یکسان هستند:
نتیجه بهدست آمده دور از انتظار نبود. زیرا، نیروی کشش باعث شتاب جعبه و سمت چپ طناب میشود. همچنین جهت نیروی اصطکاک مخالف نیروی کشش است. نمودار آزاد سیستم متشکل از جعبه و طناب در تصویر زیر نشان داده شده است.
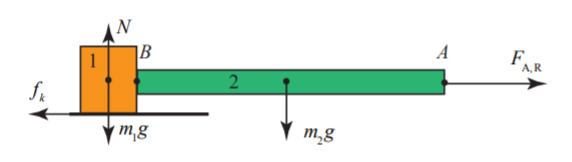
برای تصویر فوق قانون دوم نیوتن را مینویسیم:
رابطه نوشته شده در بالا را برای حل میکنیم و معادله به دست آمده برای این نیرو را در رابطه (۱) قرار میدهیم.
مثال دوم نیروی کشش طناب جرم دار
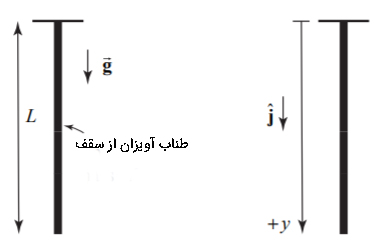
در مثال اول حالتی را در نظر گرفتیم که طناب جرمدار در حالت افقی قرار گرفته بود. اکنون حالتی را در نظر می گیریم که طناب یکنواختی به جرم M و طول L از سقف آویزان شده است. بزرگی شتاب ناشی از نیروی گرانشی برابر g است. (1) کشش طناب را در نقطه بالایی و محل اتصال به سقف به دست آورید. 2) نیروی کشش طناب را بر حسب فاصله از سقف پیدا کنید. (3) نرخ تغییرات نیروی کشش طناب را بر حسب فاصله از سقف به دست آورید.
پاسخ
قسمت (۱): دستگاه مختصات را به گونهای انتخاب میکنیم که مبدا آن بر روی سقف قرار داشته باشد و جهت مثبت آن به سمت پایین باشد. آز آنجایی که در قسمت (۱) مثال، نیروی کشش نخ را در نقطه اتصال آن به سقف میخواهیم، کل طناب را به عوان سیستم انتخاب میکنیم. نیروهایی وارد شده بر طناب در این نقطه عبارتند از:
- نیروی وارد شده بر طناب در نقطه y=0 که آن را نگه داشته است.
- نیروی وزن کل طناب.
نمودار جسم آزاد در ادامه نشان داده شده است.
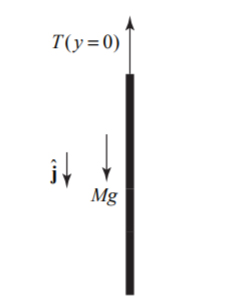
از آنجایی که طناب در حالت تعادل قرار دارد و شتاب حرکت آن برابر صفر است داریم:
Mg - T(y=0) = 0
T(y=0) = Mg
در نتیجه، نیروی کششی طناب در نقطه اتصال طناب به سقف برابر وزن آن است.
قسمت (۲): به یاد داشته باشید که نیروی کشش در هر نقطهای برابر با بزرگی جفت نیروهای عمل و عکسالعمل وارد شده در آن نقطه است. قسمت فرضی از طناب را در فاصله y از سقف در نظر میگیریم. در اینصورت، طناب به دو قسمت بالایی ۱ و پایینی ۲ تقسیم میشود. قسمت بالایی طناب را به عنوان سیستم در نظر میگیریم. جرم این قسمت برابر با است. نیروهایی که بر قسمت ۱ طناب وارد میشوند عبارتند از:
- نیروی وزن.
- نیروی T(y=0) که طناب را به سمت بالا نگه داشته است.
- نیروی کشش T(y) در نقطه y که قسمت بالایی طناب را میکشد.
نمودار جسم آزاد در ادامه نشان داده شده است.
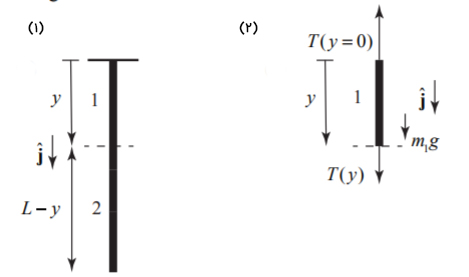
بر طبق قانون دوم نیوتن برای قسمت بالایی طناب داریم:
در نتیجه، نیروی کشش طناب در فاصله y از سقف برابر است با:
از آنجایی که جرم این قسمت از طناب برابر و Mg برابر با نیروی کشش در نقطه اتصال طناب به سقف است، بنابراین رابطه بالا به صورت زیر نوشته میشود:
رابطه (۱)
اگر در این رابطه مقدار y را برابر L قرار دهیم، نیروی کشش طناب در پایینترین نقطه برابر صفر خواهد شد. این نتیجه دور از انتظار نیست، زیرا در پایینترین نقطه طناب هیج نیرویی وارد نمیشود.
قسمت (۳): از طرفین رابطه (۱) بر حسب y مشتق میگیریم:
معادله فوق بیانگر نرخ تغییرات نیروی کشش طناب بر حسب فاصله از سقف است.
برای آشنای بیشتر با نیروی کشش، «فرادرس» اقدام به انتشار فیلم آموزش فیزیک - پایه دوازدهم کرده که لینک آن در ادامه آورده شده است.
- برای دیدن فیلم آموزش فیزیک - پایه دوازدهم + اینجا کلیک کنید.
نیروی کشش نخ در قرقره
تاکنون به پرسش نیروی کشش چیست پاسخ دادیم. در ادامه، نیروی کشش نخ را در قرقره یا ماشین آتوود به دست میآوریم. قرقره وسیلهای است که در بیشتر مسائل فیزیک از جرم آن چشمپوشی میشود و نخ یا طنابی از آن میگذرد. به هنگام حل مسائل مربوط به قرقرهها، فرضهای مختلفی در نظر گرفته میشود. به طور معمول، نخ عبوری از قرقره سبک و با طول ثابت در نظر گرفته میشود. همچنین، قرقره را یکنواخت و سبک در نظر میگیریم.
مثال اول نیروی کشش در قرقره
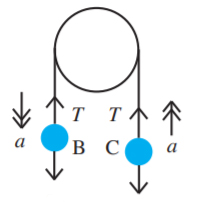
طنابی با طول ثابت و سبک از قرقره یکنواخت و سبکی عبور کرده است. به دو انتهای طناب، دو ذره B و C با جرمهای به ترتیب ۸ و ۲ کیلوگرم بسته شدهاند. اگر این دو ذره از حالت سکون رها شوند، کشش طناب و شتابهای حرکت دو جرم را به دست آورید.
پاسخ
ذکر این نکته مهم است که مقدار نیروی کشش طناب در سراسر آن ثابت و یکسان است. همچنین، شتابهای دو جرم با یکدیگر برابر ولی در خلاف جهت هم هستند.به طور معمول، برای حل این نوع مسائل هر کدام از جرمها را به طور جداگانه در نظر میگیریم و نیروهای وارد بر آنها را رسم میکنیم.
جرم B از جرم A سنگینتر است. در نتیجه، به سمت پایین حرکت خواهد کرد. قانون دوم نیوتن را برای این جرم به صورت زیر مینویسیم:
رابطه (۱)
جرم C نیز به سمت بالا حرکت میکند. بنابراین، قانون دوم نیوتن برای این جرم به صورت زیر نوشته خواهد شد:
رابطه (۲)
در دو رابطه بالا، نیروی کشش طناب و شتاب حرکت جرمها مجهول هستند. T را از رابطه (۲) به دست میآوریم و آن را در رابطه (۱) قرار میدهیم.
مقدار شتاب به دست آمده را در یکی از رابطههای بالا قرار میدهیم و نیروی کشش طناب را به دست میآوریم:
مثال دوم نیروی کشش در قرقره
جعبهای به جرم ۶ کیلوگرم بر روی سطح زبری میلغزد. این جعبه به وسیله طناب سبکی به جعبه دیگری به جرم ۴ کیلوگرم وصل شده است. این طناب از قرقره یکنواخت و سبکی عبور کرده است. اگر ضریب اصطکاک جنبشی بین جعبه و سطح میز برابر ۰/۳ باشد، شتاب حرکت هر یک از جعبهها و نیروی کشش طناب را به دست آورید.
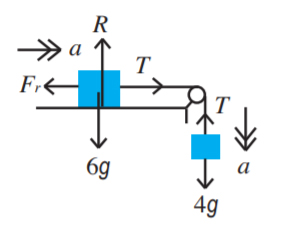
پاسخ
در ابتدا جعبه روی میز را در نظر میگیریم. بزرگی نیروی عمود بر سطح برابر نیروی وزن جعبه است. جعبه بر روی میز میلغزد، بنابراین داریم:
قانون دوم نیوتن را برای جعبه روی میز مینویسیم:
رابطه (۱)
جعبه آویزان از طناب به سمت پایین حرکت میکند. بنابراین، قانون دوم نیوتن برای آن به صورت زیر نوشته خواهد شد:
رابطه (۲)
T را از رابطه (۱) به دست میآوریم و آن را در رابطه (۲) قرار میدهیم. بنابراین داریم:
با قرار دادن مقدار به دست آمده برای شتاب در یکی از رابطههای بالا، اندازه کشش طناب را به دست میآوریم:
مثال سوم نیروی کشش در قرقره
سیستمی شامل دو قرقره و ۳ وزنه را به صورت زیر در نظر بگیرید. قرقرهها بدون جرم و بدون اصطکاک در نظر گرفته شدهاند. همچنین، طنابها را نیز بدون جرم و با طول ثابت در نظر بگیرید. قرقره بالاتر آزادانه میچرخد، اما مرکز جرم آن ساکن است. شعاع هر دو قرقره یکسان و برابر R است. (۱) رابطه بین شتاب حرکت جرمها را به دست آورید. (۲) نمودار جسم آزاد را برای هر یک از جرمها رسم کنید. (۳) شتاب حرکت اجسام و نیروهای کشش طنابها را به دست آورید.
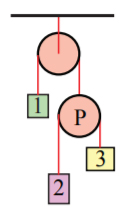
پاسخ
قسمت (۱): مرکز قرقره بالایی را به عنوان مرکز انتخاب میکنیم. مکان جرمهای ۱، ۲ و ۳ را به ترتیب با و و نشان میدهیم. همچنین، فاصله مرکز قرقره پایین از مبدا را با نشان میدهیم. جهت رو به پایین را جهت مثبت در نظر میگیریم.
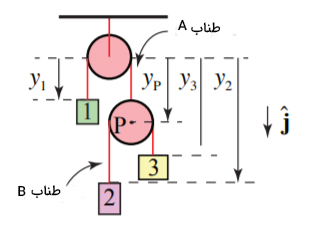
طول طناب A به صورت زیر نوشته میشود:
در رابطه بالا قسمتی از طول طناب است که در تماس با قرقره قرار دارد. از طرفین رابطه بالا نسبت به زمان دوبار مشتق میگیریم. از آنجایی که طول طناب ثابت در نظر گرفته شده است، بنابراین مشتق آن نسبت به زمان برابر صفر خواهد بود.
با توجه به رابطه فوق، شتابهای جرم ۱ و قرقره متحرک با یکدیگر برابر، ولی در خلاف جهت یکدیگر هستند:
رابطه (۱)
طول طناب B به صورت زیر نوشته می شود:
در رابطه فوق، قسمتی از طول طناب است که در تماس با قرقره قرار دارد. طول طناب B نیز ثابت است، بنابراین مشتق آن نسبت به زمان برابر صفر خواهد بود.
رابطه (۲)
با جایگزین کردن رابطه (۱) در رابطه (۲) داریم:
در نتیجه، رابطه بین شتاب حرکت سه جرم به صورت بالا به دست آمد.
قسمت (۲): در این قسمت نمودار آزاد سه جرم و قرقره متحرک را رسم میکنیم.
جرم ۱: بر جرم ۱، نیروهای وزن و نیروی کشش از طرف طناب A وارد میشوند. از آنجایی که طنابها بدون جرم و با طول ثابت در نظر گرفته شدهاند، بنابراین اندازه نیروی کشش در سراسر قرقره یکسان است. قانون دوم نیوتن برای این جرم به صورت زیر نوشته میشود:
جرم ۲: بر جرم ۲، نیروهای وزن و نیروی کشش از طرف طناب B وارد میشوند. قانون دوم نیوتن برای این جرم نیز به صورت زیر نوشته خواهد شد:
جرم ۳: بر جرم ۳ نیز نیروهای وزن و نیروی کشش از طرف طناب B وارد میشوند. ذکر این نکته مهم است که کشش نخ در سراسر قرقره B نیز یکسان است. قانون دوم نیوتن را برای این جرم به صورت زیر مینویسیم:
قرقره متحرک: نیروهای وارد شده بر قرقره متحرک یا p، نیروی وزن (در این مثال وزن قرقرهها ناچیز در نظر گرفته شده است، بنابراین مقدار نیروی وزن برابر صفر است.) و نیروی کشش طناب B است. همچنین، طناب A این قرقره را نگه داشته است. در نتیجه، نیروی کششی نیز از طرف این طناب بر قرقره p وارد می شود. قانون دوم نیوتن برای این قرقره به صورت زیر نوشته می شود:
نمودار جسم آزاد نیروهای وارد شده بر سه جرم و قرقره متحرک در تصویر زیر نشان داده شده است.
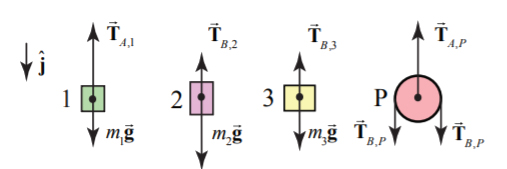
از آنجایی که قرقره متحرک بدون جرم در نظر گرفته شده است، نیروی کشش طناب A با نیروی کشش طناب B به صورت زیر به یکدیگر مربوط میشوند:
اکنون میتوانیم شتاب حرکت جرمها و نیروی کشش دو طناب را به دست آوریم:
رابطه (۳)
رابطه (4)
رابطه (۵)
رابطه (۶)
رابطه (۷)
در اینجا پنج معادله و پنج مجهول داریم، بنابراین میتوانیم به راحتی مقدارهای مجهولها را به دست آوریم. با استفاده از رابطه (۷)، کشش طناب A در رابطه (۴) را حذف میکنیم:
رابطه (۸)
سپس شتابهای حرکت سه جرم را از معادلات ۵، ۶ و ۸ به دست میآوریم:
اکنون رابطههای بدست آمده برای شتابهای حرکت سه جرم را در رابطه (۳) قرار می دهیم:
با استفاده از رابطه فوق، کشش طناب B را به دست میآوریم:
با استفاده از رابطه (۷) نیروی کشش طناب A را به دست میآوریم:
اکنون با دانستن نیروهای کشش طنابهای A و B، شتاب حرکت جرم ۱، ۲ و ۳ را به دست میآوریم:
نیروی کشش کابل آسانسور
به طور حتم از آسانسور استفاده کردهاید. آیا تاکنون کنجکاو شدهاید که نیروی کشش کابل متصل به آسانسور چقدر است؟ یا چه هنگام کابل آسانسور ممکن است پاره شود؟ در ادامه مثالی در این مورد حل میشود.
مثال نیروی کشش کابل آسانسور
نیروی کشش کابل آسانسور را برای شش حالت زیر به دست آورید:
- هنگامی که آسانسور در حال سکون و بدون حرکت است.
- آسانسور از حالت سکون به سمت بالا شتاب میگیرد. فرض کنید سرعت آسانسور پس از طی مسافت ۲۵ متر برابر ۱۰ متر بر ثانیه است.
- آسانسور از حالت سکون به سمت پایین شتاب میگیرد. فرض کنید سرعت آسانسور پس از طی مسافت ۲۵ متر برابر ۱۰ متر بر ثانیه است.
- آسانسور با سرعت ثابت ۱۰ متر بر ثانیه حرکت میکند.
- آسانسور هنگام حرکت به سمت بالا میایستد. در این قسمت فرض کنید که آسانسور با سرعت اولیه ۱۰ متر بر ثانیه در حال حرکت است و پس از طی مسافت ۲۵ متر میایستد.
- آسانسور هنگام حرکت به سمت پایین میایستد. فرض کنید آسانسور با سرعت اولیه ۱۰ متر بر ثانیه در حال حرکت است و پس از طی مسافت ۲۵ متر میایستد.
پاسخ
برای حل این مثال از دو روش استفاده میکنیم:
- روش ۱: ابتدا علامت شتاب را تعیین میکنیم. سپس آن را در معادلات حرکت و نیرو استفاده میکنیم.
- روش ۲: فرض میکنیم برای همه حالتها شتاب حرکت مثبت است. علامت شتاب با استفاده از معادلات حرکت و اطلاعات داده در مثال تعیین میشود.
روش ۱
همانگونه که در توضیحات بالا گفته شد، هنگامی که نیرویی در جهت جسمی خطی مانند کابل یا طناب قرار گرفته باشد، به آن نیروی کشش میگوییم. برای حل این مثال، جرم آسانسور را ۸۰۰ کیلوگرم و جهت به سمت بالا را مثبت در نظر میگیریم.
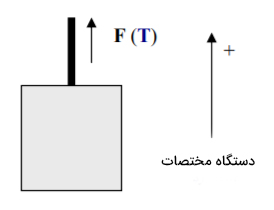
این مثال از ۶ قسمت تشکیل شده است:
قسمت ۱: نیروهای وارد شده بر آسانسور عبارتند از:
- نیروی وزن به سمت پایین.
- نیروی کشش کابل به سمت بالا.
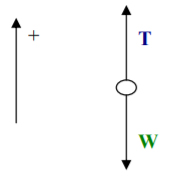
از آنجایی که آسانسور در حالت سکون قرار دارد، بنابراین برآیند نیروهای وارد بر آن در جهت عمودی برابر صفر خواهد بود:
در نتیجه، نیروی کشش کابل برابر 7840 نیوتن است.
قسمت (۲):
در این قسمت آسانسور از حالت سکون به سمت بالا شروع به حرکت میکند. پس از طی مسافت ۲۵ متر، سرعت آسانسور ۱۰ متر بر ثانیه میشود. در نتیجه، برآیند نیروهای وارد شده بر آسانسور برابر است با:
در رابطه بالا، شتاب مثبت است. اکنون، اندازه آن را به دست میآوریم. برای این کار از معادلات حرکت با شتاب ثابت استفاده میکنیم:
در نتیجه، برای نیروی کشش کابل داریم:
قسمت (۳):
در این حالت آسانسور از حالت سکون شروع به حرکت میکند و سرعت آن پس از طی مسافت ۲۵ متر برابر ۱۰ متر بر ثانیه میشود.
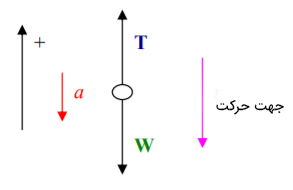
در این حالت، شتاب حرکت آسانسور منفی است. در ادامه شتاب حرکت را به دست میآوریم:
مقدار نیروی کشش کابل به صورت زیر به دست میآید:
قسمت (۴):
در این قسمت، آسانسور با سرعت ثابت ۱۰ متر بر ثانیه حرکت میکند. در نتیجه، برآیند نیروهای وارد بر آن برابر صفر است.
سوالی که ممکن است مطرح شود آن است که اگر جهت حرکت آسانسور برعکس میشد، نتیجه به دست آمده تغییری میکرد؟ پاسخ به این پرسش خیر است.
قسمت (۵):
در این قسمت آسانسور با سرعت ۱۰ متر بر ثانیه به سمت بالا در حرکت است و پس از طی مسافت ۲۵ متر میایستد. در نتیجه، جهت شتاب حرکت منفی و به سمت پایین است.
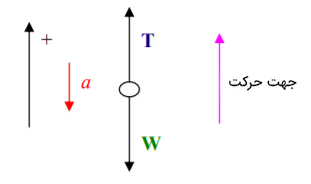
برآیند نیروهای وارد بر آسانسور برابر است با:
شتاب حرکت را به صورت زیر به دست میآوریم:
بنابراین، برای نیروی کشش کابل داریم:
قسمت (۶):
در این قسمت آسانسور با سرعت ۱۰ متر بر ثانیه به سمت پایین در حرکت است و پس از طی مسافت ۲۵ متر میایستد. جهت شتاب حرکت به سمت بالا و مثبت است.
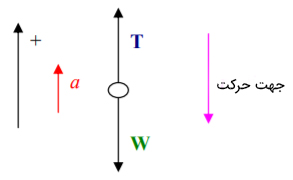
برآیند نیروهای وارد بر آسانسور برابر است با:
اندازه شتاب حرکت برابر است با:
مقدار نیروی کشش کابل نیز برابر است با:
در ادامه، برای حل این مثال از روش دوم استفاده میکنیم.
روش ۲
در روش ۲، فرض میکنیم شتاب حرکت آسانسور مثبت است. در نتیجه، نمودار آزاد آسانسور را به صورت زیر در نظر میگیریم:
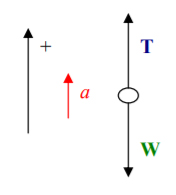
نیروس کششی کابل به صورت زیر به دست میآید:
قسمت (۱): در قسمت (۱) شتاب حرکت آسانسور برابر صفر است:
قسمت (۲): شتاب حرکت به صورت زیر به دست میآید:
برای نیروی کششی کابل داریم:
قسمت (۳): در ابتدا، شتاب حرکت را به دست میآوریم:
اندازه نیروی کششی کابل برابر است با:
قسمت (۴): در این قسمت آسانسور با سرعت ثابت حرکت میکند. در نتیجه، شتاب حرکت برابر صفر و نیروس کششی کابل برابر نیروی وزن آسانسور و مساوی 7840 نیوتن است.
قسمت (۵): آسانسور هنگام حرکت به سمت بالا در یکی از طبقات میایستد.
با جایگزینی شتاب در رابطه نیروی کششی کابل داریم:
قسمت (۶): در این قسمت آسانسور به سمت پایین در حرکت است و در یکی از طبقات میایستد:
نیروی کششی کابل برابر است با:
نیروی کششی فنر چیست ؟

هنگامی که فنری فشرده یا کشیده میشود، انرژی در آن ذخیره میشود. نیروی کششی فنر، این انرژی آزاد شده و استفاده از آن برای هدف مشخصی است.
فنر چیست ؟
فنر وسیلهای است که میتواند به وسیله نیرویی تغییر شکل دهد و پس از حذف نیرو، به شکل اولیه خود بازگردد.
فنرها شکلها و انواع متفاوتی دارند. اما فنر سیمپیچ فلزی ساده یکی از آشناترین شکلهای فنر است. فنرها یکی از ضروریترین بخشهای تمام وسایل مکانیکی ساده تا پیچیده هستند. خاصیت کشسانی سیمی که فنر از آن ساخته شده است یکی از بنیادیترین و مهمترین ویژگی آن است.
هنگامی که ماده ای تغییر شکل میدهد چه اتفاقی رخ می دهد؟
هنگامی گه نیرویی بر جسمی وارد میکنیم، آن جسم در پاسخ به نیروی وارد شده کشیده یا فشرده خواهد شد.
در فیزیک مکانیک، به نیروی وارد شده بر واحد سطح فشار یا تنش (Stress) گفته و با نشان داده میشود. به میزان فشردگی/کشیدگی ماده در اثر پاسخ به تنش وارد شده، کرنش میگوییم (). کرنش را به صورت نسبت تغییر طول به طول اولیه در امتداد تنش تعریف میکنیم:
مواد مختلف به هنگام اعمال فشار، رفتارهای متفاوتی نشان میدهند. در بیشتر مواد، میزان کرنش مواد به میزان قوی بودن پیوندهای شیمیایی آنها بستگی دارد. سختی ماده به طور مستقیم به ساختار شیمیایی آن و نوع پیوندهای شیمیایی وابسته است. همچنین، چگونگی رفتار ماده پس از حذف فشار، به مقدار حرکت اتمها تشکیلدهنده آن بستگی خواهد داشت. در حالت کلی دو نوع تغییر شکل وجود دارد
- تغییر شکل کشسان: در این حالت، ماده پس از حذف تنش به شکل اول خود بازمیگردد. این تغییر شکل بازگشتپذیر و موقت است.
- تغییر شکل ناکشسان: این تغییر شکل به هنگام اعمال تنش بزرگ اتفاق میافتد. در نتیجه، پس از حذف تنش، ماده به شکل اولیه خود بازنمیگردد. این تغییر شکل بازگشتناپذیر و دائمی است. به مقدار کمینه تنش که باعث تغییر شکل بازگشتناپذیر ماده شود، حد الاستیک میگوییم.
فنرها به گونهای طراحی میشوند که تغییر شکل کشسان داشته باشند.
قانون هوک
«رابرت هوک» (Robert Hooke) در قرن ۱۷ میلادی رابطه بین تنش و کرنش را برای بسیاری از مواد مطالعه کرد. بر طبق یافتههای او، در نمودار تنش-کرنش ناحیه خطی برای بیشتر مواد وجود دارد. نیروی اعمال شده بر جسم کشسانی مانند فنر فلزی با میزان کشیدگی یا فشردگی فنر متناسب است. این تناسب به قانون هوک معروف است و به طور معمول به صورت زیر نوشته میشود:
در رابطه بالا، F نیروی اعمال شده بر فنر، x میزان کشیدگی یا فشردگی فنر و k ثابت تناست است که به ثابت فنر شناخته میشود. واحد k نیوتن بر متر است.
در اینجا، جهت نیروی اعمال شده مشخص نشده است، اما علامت منفی در رابطه گذاشته شده است. در واقع، نیروی بازگرداننده فنر در جهت مخالف نیرویی است که که آن را فشرده کرده یا کشیده است.
برای حل مسائل مربوط به فنرهای کشسان، تعیین جهت نیروی بازگرداننده بسیار مهم است. در مسائل ساده، x به عنوان بردار یکبعدی در نظر گرفته میشود. در این حالت، نیرو نیز برداری یکبعدی است و با استفاده از قانون هوک میتوان جهت آن را تعیین کرد.
به هنگام به دست آوردن x به یاد داشته باشید که فنر قبل از فشرده شدن یا کشیدن دارای طول اولیه است. طول فنر پس از کشیدن برابر طول اولیه به اضافه میزان کشیدگی و برابر است. همچنین، طول فنر فشرده شده برابر طول اولیه منهای میزان فشردگی و مقدار خواهد بود.
مثال اول نیروی کششی فنر
شخصی به وزن ۷۵ کیلوگرم بر روی فنری با ثابت فنر ۵۰۰۰ نیوتن بر متر و طول اولیه ۰/۲۵ متر ایستاده است. طول فنر پس از فشردن را به دست آورید.
پاسخ
در ابتدا با استفاده از قانون هوک میزان فشردگی فنر را به دست میآوریم:
برای به دست آوردن طول فنر در حالت فشرده شده، طول اولیه را از میزان فشردگی کم میکنیم:
مثال دوم نیروی کششی فنر
پایهای را برای حرکت دوربینی به وزن یک کیلوگرم در راستای عمودی به اندازه ۵۰ سانتیمتر طراحی کردهاید. طراحی انجام شده در تصویر زیر نشان داده شده است. اگر طول اولیه فنر برابر ۵۰ میلیمتر باشد، کمینه ثابت فنر برای این طراحی چه مقدار است؟
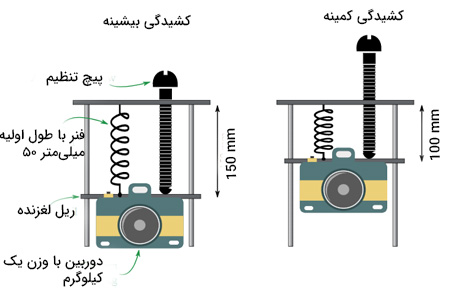
پاسخ:
فرض میکنیم فنر به اندازه کافی کشسان است. اندازه نیروی کششی هنگامی که فنر در کمینه میزان کشیدگی خود قرار دارد، بسیار ضعیف است. در این هنگام، فاصله بین بالا و پایین فنر برابر ۱۰۰ میلیمتر است. از آنجایی که اندازه فنر در حالت عادی برابر ۱۰۰ میلیمتر است، کمینه اندازه فشردگی برابر خواهد بود. نیروی کششی فنر در جهت مخلف نیروی وزن دوربین است:
معرفی فیلم آوزش فیزیک ۱ دانشگاهی با رویکرد حل مساله

مجموعه فرادرس در تولید و محتوای آموزشی خود اقدام به تهیه فیلم آموزش فیزیک ۱ دانشگاهی با رویکرد حل مساله برای دانشجویان رشته فیزیک و فنی مهندسی و دانشآموزان پایه دوازدهم کرده که این مجموعه آموزشی از هفت درس تشکیل شده است.
درس یکم در مورد اندازهگیری، دستگاه جهانی و تبدیل یکاها و ارقام معنیدار است. با بردارها، کمیتهای نردهای، جمع و تفریق بردارها، تجزیه بردارها و برآیند آنها در درس دوم آشنا میشوید. در نتیجه، پس از تماشای این درس مسائل مربوط به برآیند نیروهای وارد شده بر جسم را به راحتی حل خواهید کرد. حرکت در یک و دوبعد در درسهای سوم و چهارم آموزش داده میشوند.
با مفهوم نیرو و قوانین نیوتن در درس پنجم آشنا خواهید شد. در این درس نیروهای مختلفی مانند نیروی اصطکاک، نیروی کشش و نیروی فنر توضیح داده و مسائل گوناگونی برای درک بهتر نیروهای حل میشوند. بنابراین، پس از تماشای این درس، درک بهتری از نیروی کششی خواهید داشت. برای آشنایی با کار نیروهای مختلف، قضیه کار و انرژی و تعریف قانون پایستگی انرژی به درس ششم مراجعه کنید. در پایان، مفاهیمی مانند دما و گرما، روابط دما و قوانین ترمودینامیک همراه با حل مساله در درس هفتم آموزش داده شده است.
- برای دیدن فیلم آموزش فیزیک ۱ دانشگاهی با رویکرد حل مساله + اینجا را کلیک کنید.
معرفی فیلم آموزش فیزیک - پایه دوازدهم

مجموعه فرادرس در تولید و محتوای آموزشی اقدام به تهیه فیلم آموزش فیزیک - پایه دوازدهم برای دانشآموزان پایه دوازدهم کرده که این مجموعه اموزشی از بیست و سه درس تشکیل شده است.
درسهای یکم تا پنجم در مورد حرکت بر خط راست است. نیروی کششی فنر و طناب را در درس ششم فرا خواهید گرفت. در نتیجه، پس از مطالعه این مطلب و تماشای این درس به راحتی مسائل مربوط به این نیرو را حل خواهید کرد. با دینامیک و حرکت دایرهای در درسهای هفتم و هشتم آشنا خواهید شد. مفهوم امواج و نوسان در درسهای نهم تا هفدهم آموزش داده میشوند.
- برای دیدن فیلم آموزش فیزیک - پایه دوازدهم + اینجا کلیک کنید.
جمعبندی
در این مطلب به پرسش نیروی کششی چیست پاسخ داده شد. در ابتدا، نیروی کشش سطحی در سطح آب معرفی شد. در ادامه، نیروی کشش طناب و نخ معرفی و مثالهایی برای درک بهتر این دو نیرو حل شد. همچنین، به این نکته اشاره شد که در دنیای واقعی طنابها جرم دارند. در نتیجه، نیروی کشش در طناب جرمدار در همه جای آن یکسان نخواهد بود. برای درک بهتر این موضوع، دو مثال در مورد طناب جرمدار، در حالتهای افقی و عمودی حل شد.













سلام. سپاس از مطلب خوب تان.
ضریب کشش چیست؟