انتگرال و مشتق سری فوریه — به زبان ساده (+ دانلود فیلم آموزش رایگان)

در آموزشهای قبلی از مجموعه آموزشهای ریاضی مجله فرادرس، با سری فوریه آشنا شدیم. در این آموزش درباره انتگرال و مشتق سری فوریه بحث خواهیم کرد.
مشتق سری فوریه
فرض کنید $$f(x)$$ یک تابع تکهای پیوسته متناوب با دوره تناوب $$2\pi$$ باشد که روی بازه بسته $$\left[ { – \pi ,\pi } \right]$$ تعریف شده است.
همانطور که میدانیم، بسط سری فوریه چنین تابعی به صورت زیر است:
$$ \large { f \left ( x \right ) = \frac { { { a _ 0 } } } { 2 } } + { \sum \limits _ { n = 1 } ^ \infty { \left ( { { a _ n } \cos n x + { b _ n } \sin n x } \right ) } . } $$
اگر مشتق $$f’\left( x \right)$$ این تابع نیز تکهای پیوسته باشد و تابع $$f(x)$$ در شرایط تناوبی زیر صدق کند:
$$ \large { f \left ( { – \pi } \right ) = f \left ( \pi \right ) , \; \; \; } \kern-0.3pt{ f’ \left ( { – \pi } \right ) = f’ \left ( \pi \right ) , } $$
آنگاه بسط سری فوریه $$f’\left( x \right)$$ با فرمول زیر نشان داده میشود:
$$ \large { f’ \left ( x \right ) \text { = } } \kern0pt{ \sum \limits _ { n = 1 } ^ \infty { \left ( { n { b _ n } \cos n x – n { a _ n } \sin n x } \right ) } } . $$
انتگرال سری فوریه
اگر $$g(x)$$ یک تابع تکهای پیوسته متناوب با دوره تناوب $$2 \pi$$ روی بازه $$\left[ { – \pi ,\pi } \right]$$ باشد، آنگاه میتوان از این تابع روی این بازه جمله به جمله انتگرال گرفت. سری فوریه تابع $$g(x)$$ به صورت زیر است:
$$ \large { g \left ( x \right ) = \frac { { { a _ 0 } } } { 2 } } + { \sum \limits _ { n = 1 } ^ \infty { \left ( { { a _ n } \cos n x + { b _ n } \sin n x } \right ) } . } $$
تابع زیر را در نظر بگیرید:
$$ \large { G \left ( x \right ) = \int \limits _ 0 ^ x { g \left ( t \right ) d t } } \sim { \frac { { { A _ 0 } } } { 2 } } + { \sum \limits _ { n = 1 } ^ \infty { \left ( { { A _ n } \cos n x + { B _ n } \sin n x } \right ) } } $$
که در آن، $${A_n} = – {\large\frac{{{b_n}}}{n}\normalsize}$$ و $${B_n} = {\large\frac{{{a_n}}}{n}\normalsize}$$.
با قرار دادن $$x=0$$، داریم:
$$ \large { G \left ( 0 \right ) = 0 } = { \frac { { { A _ 0 } } } { 2 } + \sum \limits _ { n = 1 } ^ \infty { { A _ n } } } = { \frac { { { A _ 0 } } } { 2 } – \sum \limits _ { n = 1 } ^ \infty { \frac { { { b _ n } } } { n } } \; \; \text {or} \; \; } \kern-0.3pt { \frac { { { A _ 0 } } } { 2 } = \sum \limits _ { n = 1 } ^ \infty { \frac { { { b _ n } } } { n } } . } $$
بنابراین، بسط سری فوریه تابع $$G(x)$$ به صورت زیر تعریف میشود:
$$ \large \begin {align*} G \left ( x \right ) & = \int \limits _ 0 ^ x { g \left ( t \right ) d t } = { { \int \limits _ 0 ^ x { \frac { { { a _ 0 } } } { 2 } d x } \text { + }} } \kern0pt{{ \sum \limits _ { n = 1 } ^ \infty { \int \limits _ 0 ^ x { \left ( { { a _ n } \cos n x + { b _ n } \sin n x } \right ) d x } } } } \\ &= { { \frac { { { a _ 0 } x } } { 2 } \text { + }} \kern0pt{ \sum \limits _ { n = 1 } ^ \infty { \frac { { { a _ n } \sin n x + { b _ n } \left ( {1 – \cos n x } \right ) } } { n } } } } \end {align*} $$
سری به دست آمده، نتیجه انتگرالگیری جمله به جمله از سری فوریه $$g(x)$$ است.
به دلیل وجود جمله وابسته به $$x$$ در جواب حاصل، واضح است که این بسط، بسط سری فوریه انتگرال $$g(x)$$ نیست. این نتیجه را میتوان به گونهای تغییر داد که بسط سری فوریه تابع زیر باشد:
$$ \large { \Phi \left ( x \right ) } = { \int \limits _ 0 ^ x { g \left ( t \right ) d t } – \frac { { { a _ 0 } x } } { 2 } . } $$
سری فوریه تابع $$\Phi\left( x \right)$$ به صورت زیر است:
$$ \large { \Phi \left ( x \right ) = \int \limits _ 0 ^ x { g \left ( t \right ) d t } – \frac { { { a _ 0 } x } } { 2 } } = { \frac { { { A _ 0 } } } { 2 } \text { + } } \kern0pt{ \sum \limits _ { n = 1 } ^ \infty { \left ( { { A _ n } \cos n x + { B _ n } \sin n x } \right ) } , } $$
که در آن:
$$ \large { \frac { { { A _ 0 } } } { 2 } = \sum \limits _ { n = 1 } ^ \infty { \frac { { { b _ n } } } { n } } , \; \; \; } \kern0pt { { A _ n } = – \frac { { { b _ n } } } { n } , \; \; \; } \kern0pt { { B _ n } = \frac { { { a _ n } } } { n } . } $$
مثالها
در این بخش، چند مثال را درباره انتگرال و مشتق سری فوریه بررسی میکنیم.
مثال ۱
سری فوریه تابعِ
$$ \large { f \left ( x \right ) = \text {sign} \, x } =
{ \begin {cases}
- 1 , & - \pi \le x \le 0 \\
1 , & 0 \lt x \le \pi
\end {cases} , } $$
را با استفاده از بسط سری فوریه تابع $$F\left( x \right) = \left| x \right|$$ روی بازه $$\left[ { – \pi ,\pi } \right]$$ به دست آورید که به صورت زیر است:
$$ \large { F \left ( x \right ) = \left | x \right | } = { \frac { \pi }{ 2 } – \frac { 4 } { \pi } \sum \limits _ { n = 0 } ^ \infty { \frac { { \cos \left ( { 2 n + 1 } \right ) x } } { { { { \left ( { 2 n + 1 } \right ) } ^ 2 } } } } . \; } $$
حل: از آنجایی که به ازای $$x \ne 0$$، $$f\left( x \right) = F’\left( x \right)$$، داریم:
$$ \large { f \left ( x \right ) = \frac { d } { { d x } } \Big [ { \frac { \pi } { 2 } \text { − } } } \kern0pt{{ \frac { 4 } { \pi } \sum \limits _ { n = 0 } ^ \infty { \frac { { \cos \left ( { 2 n + 1 } \right ) x } } { { { { \left ( { 2 n + 1 } \right ) } ^ 2 } } } } } \Big ] } $$
يا
$$ \large f \left ( x \right ) = \frac { 4 } { \pi } \sum \limits _ { n = 0 } ^ \infty { \frac { { \sin \left ( { 2 n + 1 } \right ) x } } { { 2 n + 1 } } } . $$
نمودارهای این تابع و تقریب فوریه آن در شکل زیر نشان داده شده است.
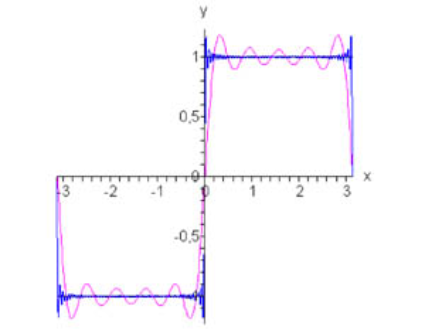
مثال ۲
بسط سری فوریه تابع $$f\left( x \right) = {x^2}$$ را با استفاده از سری فوریه زیر بیابید.
$$ \large { x = 2 \sum \limits _ { n = 1 } ^ \infty { \frac { { { { \left ( { – 1 } \right ) } ^ { n + 1 } } } } { n } \sin n x } \; \; \; } \kern-0.3pt
{ \text {for}\; – \pi \le x \le \pi . } $$
حل: از آنجایی که $$f\left( x \right)$$ روی بازه $$\left[ { – \pi ,\pi } \right]$$ یک تابع تکهای پیوسته است، میتوانیم از این سری فوریه انتگرال بگیریم:
$$ \large { \int \limits _ { – \pi } ^ x { t d t } \text { = } } \kern0pt { 2 \sum \limits _ { n = 1 } ^ \infty { \int \limits _ { – \pi } ^ x { \frac { { { { \left ( { – 1 } \right ) } ^ { n + 1 } } } } { n } \sin n t \, d t } } . } $$
در نتیجه:
$$ \large \begin{align*} & \frac { { { x ^ 2 } } } { 2 } – \frac { { { \pi ^ 2 } } } { 2 } = \kern0pt { 2 \sum \limits _ { n = 1 } ^ \infty { { { \left ( { – 1 } \right ) } ^ { n + 1 } } \left [ { \left . { \left ( { – \frac { { \cos n t } } { { { n ^ 2 } } } } \right ) } \right | _ { – \pi } ^ x } \right ] } , \; \; } \\ & \Rightarrow
{ { \frac { { { x ^ 2 } } } { 2 } – \frac { { { \pi ^ 2 } } } { 2 } \text { = } } } \kern0pt{ { 2 \sum \limits _ { n = 1 } ^ \infty { \frac { { { { \left ( { – 1 } \right ) } ^ n } } } { { { n ^ 2 } } } \left[ {\cos n x } \right . } - { \left . { \cos \left ( { – \pi n } \right ) } \right ] } , \; \; } } \\ & \Rightarrow
{ { \frac { { { x ^ 2 } } } { 2 } – \frac {{ { \pi ^ 2 } } } { 2 } } = { 2 \sum \limits _ { n = 1 } ^ \infty { \frac { { { { \left ( { – 1 } \right ) } ^ n } } } { { { n ^ 2 } } } \cos n x } } } -{ { 2 \sum \limits _ { n = 1 } ^ \infty { \frac { { { { \left ( { – 1 } \right ) } ^ n } { { \left ( { – 1 } \right ) } ^ n } } } { { { n ^ 2 } } } } , \; \; } } \\ & \Rightarrow
{ { \frac { { { x ^ 2 } } } { 2 } – \frac { { { \pi ^ 2 } } } { 2 } } = { 2 \sum \limits _ { n = 1 } ^ \infty { \frac { { { { \left ( { – 1 } \right ) } ^ n } } } { { { n ^ 2 }} } \cos n x } } } - { { 2 \sum \limits _ { n = 1 } ^ \infty { \frac { 1 }{ { { n ^ 2 } } } } . } } \end {align*} $$
طبق قضیه پارسوال و نامساوی بسل که $$\zeta \left( 2 \right) = \sum\limits_{n = 1}^\infty {\large\frac{1}{{{n^2}}}\normalsize}$$ است، خواهیم داشت:
$$ \large { { x ^ 2 } – { \pi ^ 2 } } = { 4 \sum \limits _ { n = 1 } ^ \infty { \frac { { { { \left ( { – 1 } \right ) } ^ n } } }{ { { n ^ 2 } } } \cos n x } } - { \frac { { 2 { \pi ^ 2 } } } { 3 } } $$
یا
$$ \large { { x ^ 2 } = \frac { { { \pi ^ 2 } } } { 3 } } + { 4 \sum \limits _ { n = 1 } ^ \infty { \frac { { { { \left ( { – 1 } \right ) } ^ n } } } { { { n ^ 2 } } } \cos n x } . } $$
مثال ۳
سری فوریه تابع $$f\left( x \right) = {x^3}$$ را به کمک بسط سری فوریه زیر به دست آورید.
$$ \large { { x ^ 2 } = \frac { { { \pi ^ 2 } } } { 3 } } + { 4 \sum \limits _ { n = 1 } ^ \infty { \frac { { { { \left ( { – 1 } \right ) } ^ n } } } { { { n ^ 2 } } } \cos n x } \; \; \; } \kern-0.3pt
{ \text{for} \; – \pi \le x \le \pi . } $$
حل: با انتگرال گرفتن از این سری داریم:
$$ \large \begin {align*} \require {cancel} &
{ { \int \limits _ { – \pi } ^ x { { t ^ 2 } d t } } = { \int \limits _ { – \pi } ^ x { \frac { { { \pi ^ 2 } } } { 3 } d t } } + { 4 \sum \limits _ { n = 1 } ^ \infty { { { \left ( { – 1 } \right ) } ^ n } \int \limits _ { – \pi } ^ x { \frac { { \cos n t } }{ { { n ^ 2 } } } d t } } , \; \; } } \\ & \Rightarrow
{ { \left . { \left ( { \frac { { { t ^ 3 } } } { 3 } } \right ) } \right | _ { – \pi } ^ \pi } = { \left . { \left ( { \frac { { { \pi ^ 2 } } } { 3 } t } \right ) } \right | _ { – \pi } ^ x } } + { { 4 \sum \limits _ { n = 1 } ^ \infty { { { \left ( { – 1 } \right ) } ^ n } \left [ { \left . { \left ( { \frac { { \sin n t } } { { { n ^ 3 } } } } \right ) } \right | _ { – \pi } ^ x } \right ] } , \; \; } } \\ & \Rightarrow
{ { \frac { { { x ^ 3 } } } { 3 } + \cancel { \frac { { { \pi ^ 3 } } } { 3 } } } = { \frac { { { \pi ^ 2 } x } } { 3 } + \cancel { \frac { { { \pi ^ 3 } } } { 3 } } } } + { { 4 \sum \limits _ { n = 1 } ^ \infty { { { \left ( { – 1 } \right ) } ^ n } \frac { { \sin n x } } { { { n ^ 3 } } } } , \; \; } } \\ & \Rightarrow
{ { { x ^ 3 } = { \pi ^ 2 } x } + { 1 2 \sum \limits _ { n = 1 } ^ \infty { \frac { { { { \left ( { – 1 } \right ) } ^ n } } }{ { { n ^ 3 } } } \sin n x } . } } \end {align*} $$
بسط سری فوریه تابع $$x$$ به شکل زیر است:
$$ \large x = 2 \sum \limits _ { n = 1 } ^ \infty { \frac { { { { \left ( { – 1 } \right ) } ^ {n+1} } } } { n } \sin n x } . $$
با قرار دادن این بسط در عبارت فوق، خواهیم داشت:
$$ \large \begin {align*} { { x ^ 3 } } & = { 2 { \pi ^ 2 } \sum \limits _ { n = 1 } ^ \infty { \frac { { { { \left ( { – 1 } \right ) } ^ { n + 1 } } } } { n } \sin nx} } + { 1 2 \sum \limits _ { n = 1 } ^ \infty { \frac { { { { \left ( { – 1 } \right ) } ^ n } } } { { { n ^ 3 } } } \sin n x } } \\ & = { { \sum \limits _ { n = 1 } ^ \infty { { { \left ( { – 1 } \right ) } ^ n } \left ( { \frac { { 1 2 } } { { { n ^ 3 } } } – \frac { { 2 { \pi ^ 2 } } } { n } } \right ) } \kern0pt{ \sin n x } } } \end {align*} $$
مثال ۴
مشتقگیری از بسط سری فوریه تابع $$f(x)=x$$ که روی بازه $$\left[ { – \pi ,\pi } \right]$$ تعریف شده است را بررسی کنید.
حل: بسط سری فوریه این تابع خطی به صورت زیر است:
$$ \large x = 2 \sum \limits _ { n = 1 } ^ \infty { { { \left ( { – 1 } \right ) } ^ { n + 1 } } \frac { { \sin n x} } { n } } . $$
با مشتق گرفتن از این بسط به رابطه زیر میرسیم:
$$ \large { 1 \sim 2 \sum \limits _ { n = 1 } ^ \infty { { { \left ( { – 1 } \right ) } ^ { n + 1 } } \cos n x } } = { 2 \left ( { \cos x – \cos 2 x } \right . } + { \left . { \cos 3 x – \ldots } \right ) . } $$
در اینجا با یک تناقض روبهرو میشویم، زیرا سری فوریه 1 باید شامل تنها یک جمله ثابت باشد. برای توضیح این تناقض، تابع دلتای دیراک یا تابع ضربه واحد $$\delta \left( x \right)$$ را معرفی میکنیم. تعریف ضعیف تابع دلتا بیان میکند که
$$ \large \delta \left ( x \right ) =
\begin {cases}
0 , & x \ne 0 \\
\infty , & x = 0
\end {cases} $$
مساحت کل زیر نمودار این تابع برابر با یک است:
$$ \large \int \limits _ { – \infty } ^ \infty { \delta \left ( x \right ) d x } = 1 . $$
تابع دلتا به صورت زیر نیز تعریف میشود:
$$ \large { \delta \left ( x \right ) } = { \mathop { \lim } \limits _ { n \to \infty } \frac { 1 } { { 2 \pi } } \frac { { \sin \left ( { n + \frac { 1 } { 2 } } \right ) x } } { { \sin \frac { x } { 2 } } } . } $$
نمودار تابع دلتا به ازای $$n=5$$ و $$n=20$$ در شکل زیر نشان داده شده است.
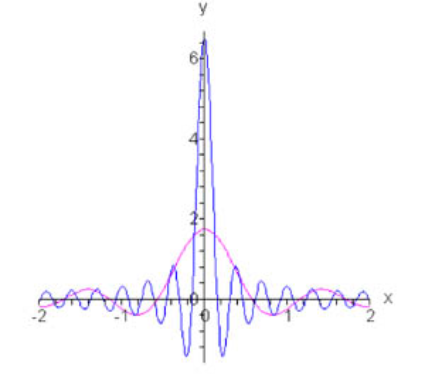
سری فوریه این تابع به صورت زیر است:
$$ \large \begin {align*} { \delta \left ( x \right ) } & = { \frac { 1 } { { 2 \pi } } + \frac { 1 } { \pi } \sum \limits _ { n = 1 } ^ \infty { \cos n x } } \\ &= { \frac { 1 } { { 2 \pi } } } + { \frac { 1 } { \pi } \sum \limits _ { n = 1 } ^ \infty { \left ( { \cos x + \cos 2 x } \right . } } + { { \left . { \cos 3 x + \ldots } \right ) } } \end {align*} $$
از آنجایی که تابع دلتا تابعی زوج است، این سری فقط شامل کسینوس خواهد بود.
اکنون بسط متناوب $${f_1}\left( x \right)$$ تابع $$f\left( x \right)$$ را بررسی میکنیم (شکل ۳).
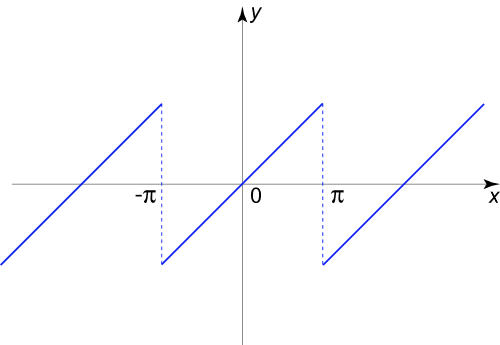
این تابع در نقاط $$x = \left( {2m + 1} \right)\pi$$ ($$m = 0, \pm 1, \pm 2, \ldots$$) دارای ناپیوستگیهای جهشی است. همچنین، مشتق بسط متناوب $${f’_1}\left( x \right)$$ در هر ناپیوستگی جهشی، یک تابع دلتای اضافه متمرکز دارد. بنابراین:
$$ \large { { f’ _ 1 } \left ( x \right ) } = { 1 \text { − }} \kern0pt{ 2 \pi \sum \limits _ { m = – \infty } ^ \infty { \delta \left [ { x – \left ( { 2 m + 1 } \right ) \pi } \right ] } } = { 1 – 2 \pi \bar \delta \left ( { x – \pi } \right ) , } $$
که در آن، $$\bar \delta \left( {x – \pi } \right)$$ بسط متناوب تابع دلتا با دوره تناوب $$2 \pi$$ را نشان میدهد.
با استفاده از سری فوریه تابع دلتا میتوان نوشت:
$$ \large \begin {align*} \delta \left [ { x – \left ( { 2 m + 1 } \right ) \pi } \right ] & = \kern0pt
{ { \frac { 1 } { { 2 \pi } } } + { \frac { 1 } { \pi } \sum \limits _ { n = 1 } ^ \infty { \cos n \left [ { x – \left ( { 2 m + 1 } \right ) \pi } \right ] } } } \\ &
= { { \frac { 1 } { { 2 \pi } } } + { \frac { 1 } { \pi } \left\{ { \cos \left [ { x – \left ( { 2 m + 1 } \right ) \pi } \right ] } \right . } } + { { \left . { \cos 2 \left [ { x – \left ( { 2 m + 1 } \right ) \pi } \right ] + \ldots } \right \} } } \\ &
= { { \frac { 1 } { { 2 \pi } } } + { \frac { 1 } { \pi } \left\{ { – \cos x + \cos 2 x }\right . } } - { { \left . { \cos 3 x + \cos 4 x – \ldots } \right\} } }
\\ & = { { \frac { 1 } { { 2 \pi } } } - { \frac { 1 } { \pi } \sum \limits _ { n = 1 } ^ \infty { { { \left ( { – 1 } \right ) } ^ { n + 1 } } \cos n x } . } } \end {align*} $$
از این رو، بسط سری فوریه $${f’_1}\left( x \right)$$ به این صورت خواهد بود:
$$ \large { { f _ 1 } ^ \prime \left ( x \right ) } = { 1 – 2 \pi \bar \delta \left ( { x – \pi } \right ) } = { 2 \sum \limits _ { n = 1 } ^ \infty { { { \left ( { – 1 } \right ) } ^ { n + 1 } } \cos n x } } \sim { 1 . } $$
بنابراین، تابع $${f_1}^\prime \left( x \right) =1 – 2\pi \bar \delta \left( {x – \pi } \right)$$ بسط سری فوریه 1 است. نمودار این تابع در شکل زیر نشان داده شده است.
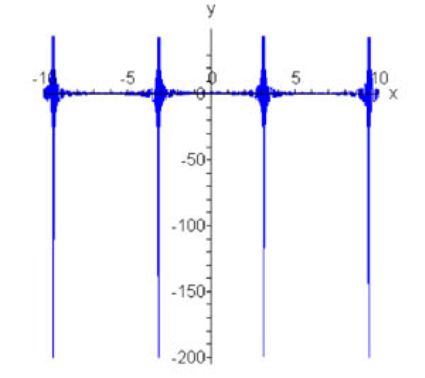
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- آموزش تجزیه و تحلیل سیگنال ها و سیستم ها
- سری فوریه مختلط — به زبان ساده
- تبدیل فوریه (Fourier Transform) — به زبان ساده
- همگرایی سری فوریه — از صفر تا صد
^^










