ماتریس هیلبرت — به زبان ساده

در این آموزش با ماتریس هیلبرت آشنا می‌شویم که در پردازش تصویر و رمزنگاری کاربرد دارد.

ماتریس هیلبرت

«ماتریس هیلبرت» (Hilbert Matrix) یک ماتریس مربعی است که درایه‌های آن کسرهای واحد و به صورت زیر هستند (کسر واحد کسری است که صورت آن ۱ و مخرجش یک عدد صحیح مثبت باشد):

$$ h _ { i j } = \frac { 1 } { i + j - 1 } . $$

فیلم آموزش ماتریس ها و جبر خطی – حل مثال و تست کنکور کارشناسی ارشد در فرادرس

کلیک کنید

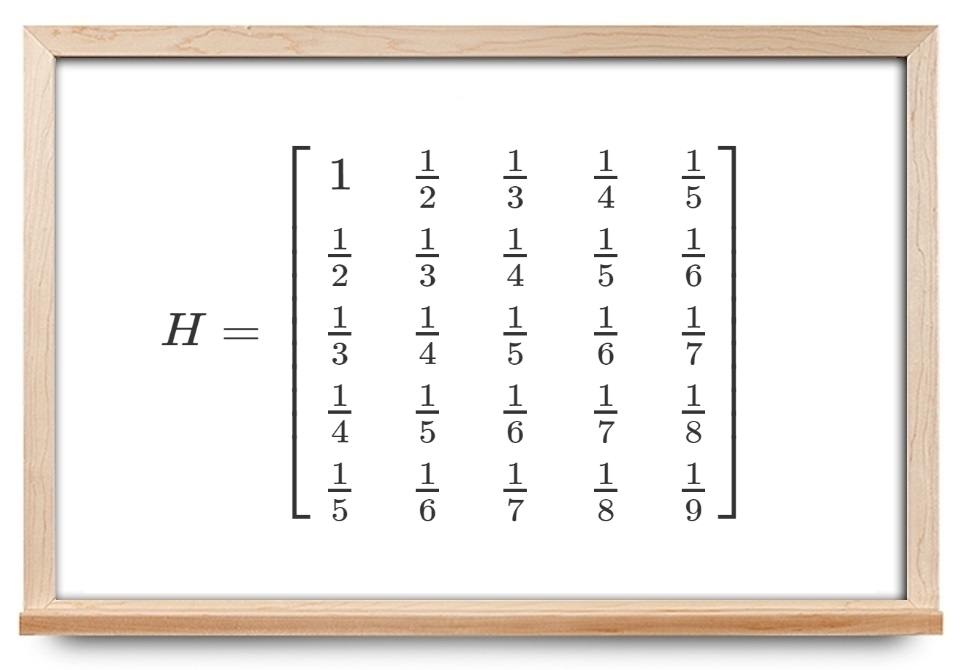
برای مثال، ماتریس زیر یک ماتریس هیلبرت $$ 5 \times 5 $$ است:

$$ H = \begin {bmatrix}
1 & \frac { 1 } { 2 } & \frac { 1 } { 3 } & \frac { 1 } { 4 } & \frac { 1 } { 5 } \\
\frac { 1 } { 2 } & \frac { 1 } { 3 } & \frac { 1 } { 4 } & \frac { 1 } { 5 } & \frac { 1 } { 6 } \\
\frac { 1 } { 3 } & \frac { 1 } { 4 } & \frac { 1 } { 5 } & \frac { 1 } { 6 } & \frac { 1 } { 7 } \\
\frac { 1 } { 4 } & \frac { 1 } { 5 } & \frac { 1 } { 6 } & \frac { 1 } { 7 } & \frac { 1 } { 8 } \\
\frac { 1 } { 5 } & \frac { 1 } { 6 } & \frac { 1 } { 7 } & \frac { 1 } { 8 } & \frac { 1 } { 9 }
\end {bmatrix} . $$

درایه‌های ماتریس هیلبرت را می‌توان از انتگرال زیر به دست آورد:

$$ h _ { i j } = \int _ 0 ^ 1 x ^ { i + j - 2 } \, d x $$

که مشابه یک «ماتریس گرامیان» (Gramian Matrix) برحسب توان‌های مختلف $$ x $$ است. فرمول بالا در واقع از تقریب حداقل مربعات توابع دلخواه توسط چندجمله‌ای‌ها می‌آید.

ماتریس‌های هیلبرت نمونه‌هایی از ماتریس‌های «بدحالت» یا «بدوضع» (ill-Conditioned) هستند که استفاده از آن‌ها در محاسبات عددی با دشواری‌هایی همراه است. برای مثال، عدد حالت نُرم ۲ ماتریس بالا تقریباً $$ 4.8 \times 10 ^ 5 $$ است.

ویژگی‌های ماتریس هیلبرت

ماتریس هیلبرت یک ماتریس متقارن و معین مثبت است. این ماتریس همچنین «کاملاً مثبت» (Totally Positive) است، یعنی دترمینان هر زیرماتریس از آن مثبت است. علاوه بر این، ماتریس هیلبرت مثالی از یک «ماتریس هنکل» (Hankel Matrix) و یک «ماتریس کوشی» (Cauchy Matrix) نیز هست.

فیلم آموزش جبر خطی در فرادرس

کلیک کنید

همان‌طور که می‌دانیم، در ماتریس هنکل $$ a _ {i j } $$ تابعی از $$ i + j $$ است و در ماتریس کوشی $$ a_{i,j} = 1/(x_i - y_j) $$ است و می‌بینیم که ماتریس هیلبرت با توجه به $$ h _ { i j } = \frac { 1 } { i + j - 1 }  $$ یک ماتریس هنکل و بر اساس تساوی $$ x_i-y_j = i+j-1 $$ یک حالت خاص از ماتریس کوشی است.

دترمینان ماتریس هیلبرت را می‌توان به فرم بسته، به عنوان یک حالت خاص از دترمینان کوشی، توصیف کرد. دترمینان ماتریس هیلبرت $$ n \times n $$ برابر است با:

$$ \det ( H ) = \frac { c _ n ^ 4 } { c _ { 2 n } } $$

که در آن:

$$ c _ n = \prod _ { i = 1 } ^ { n - 1 } i ^ { n - i } = \prod _ { i = 1 } ^ { n - 1 } i ! . $$

البته هیلبرت پیش‌تر گفته بود که دترمینان ماتریس هیلبرت وارون یک عدد صحیح است که از تساوی زیر پیروی می‌کند:

$$ \frac { 1 } { \det ( H ) } = \frac { c _ { 2 n } } { c _ n ^ 4 } = n ! \cdot \prod _ { i = 1 } ^ { 2 n - 1 } \binom { i } { [i / 2 ] } . $$

با استفاده از تقریب استرلینگ برای فاکتوریل، می‌توان عبارت زیر را نتیجه گرفت:‌

$$ \det ( H ) = a _ n \, n ^ { - 1 / 4 } ( 2 \pi ) ^ n \, 4 ^ { - n ^ 2 } $$

که در آن، وقتی $$n$$ به بینهایت میل کند، $$ a _ n $$ به مقدار ثابت $$ e^{1/4}\, 2^{1/12}\, A^{-3} \approx 0.6450 $$ همگرا می‌شود که در آن، $$ A $$ «ثابت گلیشر-کینکلین» (Glaisher–Kinkelin Constant) و تقریباً $$ A\approx1.2824271291\dots $$ است.

معکوس ماتریس هیلبرت را می‌توان با استفاده از ضرایب دوجمله‌ای به فرم بسته نشان داد که در این صورت، درایه‌های آن برابر هستند با:

$$ ( H ^ { - 1 } ) _ { i j } = ( - 1 ) ^ { i + j } ( i + j - 1 ) \binom { n + i - 1 } { n - j } \binom { n + j - 1 } { n - i } \binom { i + j - 2 } { i - 1 } ^ 2 $$

که در آن، $$ n$$ بعد ماتریس است. همان‌طور که مشخص است، درایه‌های معکوس ماتریس هیلبرت اعداد صحیح بوده و درایه‌های سطری یا ستونی آن به صورت یک در میان مثبت و منفی هستند. همچنین، درایه‌های قطر اصلی آن نیز همگی اعدادی مثبت هستند. برای مثال:

$$ \begin {bmatrix}
1 & \frac { 1 } { 2 } & \frac { 1 } { 3 } & \frac { 1 } { 4 } & \frac { 1 } { 5 } \\
\frac { 1 } { 2 } & \frac { 1 } { 3 } & \frac { 1 } { 4 } & \frac { 1 } { 5 } & \frac { 1 } { 6 } \\
\frac { 1 } { 3 } & \frac { 1 } { 4 } & \frac { 1 } { 5 } & \frac { 1 } { 6 } & \frac { 1 } { 7 } \\
\frac { 1 } { 4 } & \frac { 1} { 5 } & \frac { 1 } { 6 } & \frac { 1 } { 7 } & \frac { 1 } { 8 } \\
\frac { 1 } { 5 } & \frac { 1 } { 6 } & \frac { 1 } { 7 } & \frac { 1 } { 8 } & \frac { 1 } { 9 }
\end {bmatrix} ^ { - 1 } =
\left [ \begin {array} { r r r r r }
2 5 & - 3 0 0 & 1 0 5 0 & - 1 4 0 0 & 6 3 0 \\
- 3 0 0 & 4 8 0 0 & - 1 8 9 0 0 & 2 6 8 8 0 & - 1 2 6 0 0 \\
1 0 5 0 & - 1 8 9 0 0 & 7 9 3 8 0 & - 1 1 7 6 0 0 & 5 6 7 0 0 \\
- 1 4 0 0 & 2 6 8 8 0 & - 1 1 7 6 0 0 & 1 7 9 2 0 0 & - 8 8 2 0 0 \\
6 3 0 & - 1 2 6 0 0 & 5 6 7 0 0 & - 8 8 2 0 0 & 4 4 1 0 0
\end {array} \right ] . $$

ماتریس هیلبرت در متلب

در متلب تابعی برای تولید ماتریس هیلبرت وجود دارد. این تابع hilb است. در واقع، H = hilb (n) یک ماتریس هیلبرت مرتبه $$n$$ را نتیجه خواهد داد که درایه‌های آن $$ H ( i , j ) = 1 / ( i + j - 1 ) $$ است.

فیلم آموزش جبر خطی با متلب در فرادرس

کلیک کنید

برای مثال، با دستور زیر در متلب می‌توان یک ماتریس هیلبرت ۴ در ۴ تولید کرد:

1H = hilb(4)

اگر دستور بالا را اجرا کنیم، نتیجه آن به صورت زیر خواهد بود:

H = 4×4

    1.0000    0.5000    0.3333    0.2500
    0.5000    0.3333    0.2500    0.2000
    0.3333    0.2500    0.2000    0.1667
    0.2500    0.2000    0.1667    0.1429

همان‌طور که گفتیم، ماتریس هیلبرت یک ماتریس بدحالت است. برای بررسی این موضوع، عدد حالت ماتریس بالا را با استفاده از دستور cond محاسبه می‌کنیم:

1cond(H)

نتیجه اجرای این دستور، بدحالت بودن ماتریس را به خوبی نشان می‌دهد:

ans = 1.5514e+04

گر علاقه‌مند به یادگیری مباحث مشابه مطلب بالا هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس ریاضیات
• آموزش جبر خطی با متلب
• مجموعه آموزش‌های پردازش تصویر و ویدئو
• آموزش پردازش تصویر در متلب
• تجزیه مقادیر منفرد (SVD) — به زبان ساده
• پردازش تصویر با پایتون — راهنمای کاربردی
• تقلب نامه (Cheat Sheet) جبر خطی برای یادگیری ماشین — راهنمای سریع و کامل

^^