فیلتر وفقی چیست؟ — از صفر تا صد

امروزه فیلترهای وفقی یا فیلترهای تطبیقی (Adaptive Filter) به دلیل پردازنده‌های سیگنال دیجیتال قوی و پیشرفت‌های الگوریتم‌های وفقی جدید، در کاربردهای بسیار متنوعی مورد استفاده قرار می‌گیرند. در طول دو دهه اخیر، تعداد کاربردهایی که یک فیلتر وفقی در آن مورد استفاده قرار می‌گیرد، به صورت روز افزون در حال افزایش است. گستره وسیعی از پیکربندی‌ها وجود دارند که می‌توانند به عنوان یک فیلتر وفقی در حوزه‌های علوم مختلف مانند مخابرات، رادار، سونار، پردازش سیگنال‌های صوتی و رادیویی و حذف نویز به کار گرفته شوند. در این مطلب قصد داریم پیکربندی‌های مختلف فیلتر وفقی را بررسی کنیم و به صورت عمده روی کاربردهای اخیر فیلترهای وفقی در دنیای واقعی تمرکز می‌کنیم.

فیلتر وفقی

بازده یک فیلتر وفقی به صورت مشهودی بر تکنیک‌های طراحی خاص و الگوریتم وفقی مورد استفاده بستگی دارد. فیلترهای تطبیقی می‌توانند طراحی آنالوگ، دیجیتال و یا ترکیبی از هر دو را داشته باشند که هر کدام دارای مزایا و معایب خاص خود هستند.

به عنوان مثال، فیلترهای آنالوگ توان بسیار پایینی مصرف می‌کنند و پاسخ بسیار سریعی دارند، اما در عوض این فیلترها از خود مشکلات آفست نشان می‌دهند که بر عملکرد فیلتر وفقی تاثیر منفی می‌گذارد.

از طرف دیگر، فیلترهای دیجیتال، بدون آفست هستند و راه حلی برای ارائه دقت بالاتر محسوب می‌شوند. همچنین فیلترهای وفقی می‌توانند ترکیبی از انواع مختلف فیلتر مانند تک ورودی، فیلترهای چند ورودی، فیلترهای خطی و غیرخطی، فیلترهای پاسخ ضربه محدود (Finite Impulse Response) یا FIR و پاسخ ضربه نامحدود (Infinite Impulse Response) یاIIR باشند.

قابلیت تطبیق پارامترهای یک فیلتر وفقی بر اساس کمینه سازی خطای مجموع مربعات (Mean Squared Error) بین سیگنال خروجی از سیستم و سیگنال مطلوب ما است. حداقل مربعات بازگشتی (Recursive Least Square) یا RLS و حداقل میانگین مربعات (Least Mean Square) یا LMS متداول‌ترین انواع الگوریتم‌های فیلتر وفقی محسوب می‌شوند. یک الگوریتم RLS سرعت همگرایی بسیار بالاتری را نسبت به الگوریتم LMS دارد، اما از نظر پیچیدگی الگوریتم، الگوریتم LMS نسبت به الگوریتم RLS برتری دارد.

به دلیل سادگی محاسبات، الگوریتم LMS در طراحی و پیاده سازی فیلترهای وفقی بیشتر مورد استفاده قرار می‌گیرد. الگوریتم دیجیتال LMS مبتنی بر گرادیان نزولی است و به صورت زیر بیان می‌شود:

$$w ( n + 1 ) = w ( n ) + μ e ( n ) x ( n )$$

در رابطه فوق، $$w ( n )$$ بردار وزن‌ها در لحظه n و $$w ( n + 1 )$$ برابر با بردار وزن‌ها در لحظه n + 1 و $$x ( n )$$ بردار ورودی‌ها است که در خط تاخیر فیلتر ذخیره شده است. $$e(n)$$ متناظر با خطای فیلتر است که به صورت خطای بین سیگنال مطلوب و سیگنال خروجی فیلتر تعریف می‌شود. همچنین در رابطه فوق، $$μ$$ فاکتور همگرایی فیلتر است و به صورت غیر مستقیم با خطای کمینه متناسب است. به این ترتیب بین سرعت همگرایی و خطای کمینه یک رابطه برقرار می‌شود.

کاربرد یک فیلتر وفقی به پیکربندی فیلتر مورد استفاده بستگی دارد. پیکربندی کلاسیک یک فیلتر وفقی در شناسایی سیستم، پیش‌بینی، «حذف نویز» (Noise Cancellation) و مدلسازی معکوس مورد استفاده قرار می‌گیرد. تفاوت بین پیکربندی‌ها به نحوه استفاده از ورودی‌ها، سیگنال مطلوب و سیگنال خروجی بستگی دارد.

کاربرد فیلتر تطبیقی در شناسایی سیستم

«شناسایی سیستم» (System Identification) یک روش برای مدلسازی سیستم‌های ناشناخته محسوب می‌شود. در این روش، سیستم ناشناخته به صورت موازی با فیلتر وفقی قرار می‌گیرد و هر دو سیستم را توسط یک سیگنال یکسان تحریک می‌کنند. زمانی که مجموع مربعات خطا کمینه شود، آن‌گاه می‌توان گفت که فیلتر وفقی همان مدل مطلوب سیستم را نشان می‌دهد.

ساختاری که برای شناسایی سیستم وفقی مورد استفاده قرار می‌گیرد، در تصویر زیر نمایش داده شده است.

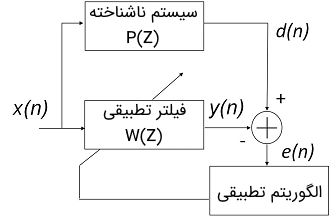
در این ساختار، $$P ( z )$$ برابر با سیستم ناشناخته است که قصد مدلسازی آن را داریم و $$W ( z )$$ نیز فیلتر وفقی مورد استفاده است. این دو سیستم توسط سیگنال $$x ( n )$$ تحریک می‌شوند. همچنین سیگنال مطلوب $$d ( n )$$ خروجی سیستم ناشناخته است. از طریق کمینه کردن خطای بین $$d(n)$$ و $$y(n)$$، می‌توان مشخصه‌های سیستم $$P(z)$$ را توصیف کرد.

خطای تخمین را می‌توان به صورت زیر نوشت:

$$e ( n ) = d ( n ) − y ( n ) = \sum_ { l = 0 } ^ { L − 1 } \; [ p ( l ) − w _ 1 ( n ) ] x ( n − l )$$

در رابطه فوق، $$p ( l )$$ برابر با پاسخ ضربه سیستم ناشناخته است و با انتخاب هر $$w _ 1 ( n )$$ نزدیک به $$p ( l )$$ مقدار خطا کاهش می‌یابد. با استفاده از نویز سفید به عنوان سیگنال تحریک، کمینه سازی $$e(n)$$ باعث نزدیک شدن سیگنال $$w _ 1 ( n )$$ به سیگنال $$p ( l )$$ می‌شود.

$$w _ 1 ( n ) ≈ p ( l ) , l = 0 , 1 , . . . , L – 1$$

زمانی که اختلاف بین پاسخ سیستم فیزیکی $$d ( n)$$ و پاسخ مدل وفقی $$y ( n)$$ کمینه شود، می‌توان گفت که مدل وفقی توانسته $$P ( z )$$ را از منظر ورودی خروجی تقریب بزند. زمانی که پلنت مورد نظر متغیر با زمان باشد، الگوریتم وفقی نقش حفظ خطای مدلسازی در یک مقدار کوچک را دارد و این کار را به صورت تعقیب پیوسته تغیرات زمانی دینامیک پلنت انجام می‌دهد.

معمولا سیگنال ورودی، یک سیگنال با پهنای باند بزرگ است تا به فیلتر امکان داده شود که برای سیستم ناشناخته به یک مدل خوب دست یابد. اگر سیگنال ورودی یک نویز سفید باشد، بهترین مدل برای سیستم ناشناخته، مدلی است که پاسخ ضربه آن با N+1 نمونه اولیه پاسخ ضربه سیستم ناشناخته همخوانی داشته باشد. در مواردی که پاسخ ضربه سیستم ناشناخته دارای طول محدود و فیلتر وفقی از مرتبه مناسب باشد، به شرط این که نویز اندازه‌گیری یا نویز کانال وجود نداشته باشد، آن گاه مقدار معیار MSE برابر با صفر به دست می‌آید.

البته باید به این نکته توجه کرد که در کاربردهای عملی وجود نویز اندازه‌گیری غیر قابل اجتناب است. در صورتی که این نویز با سیگنال ورودی وابستگی نداشته باشد یا به عبارت دیگر Uncorrelated باشند، آن گاه مقدار مورد انتظار برای ضرایب فیلتر وفقی با نمونه‌های پاسخ ضربه سیستم ناشناخته همخوانی خواهند داشت. مشخص است که مقدار خطای خروجی با مقدار نویز اندازه‌گیری برابر خواهد بود. برخی از کاربردهای واقعی برای شناسایی سیستم وفقی در زمینه سیستم‌های کنترلی و نیز تحقیقات لرزه‌شناسی است.

فیلترهای وفقی در پیش‌بینی‌ کننده‌های خطی (Linear Predictor)

یک پیش‌بینی کننده خطی مقدار سیگنال را در زمانی در آینده تقریب می‌زند. این مدل به صورت گسترده در مواردی مانند پردازش گفتار شامل «کدگذاری گفتار در مخابرات سلولی» (Speech Coding in Cellular Telephony) و «ارتقای گفتار» (Speech Enhancement) و «بازشناسی گفتار» (Speech Recognition) مورد استفاده قرار می‌گیرد. در این پیکربندی، سیگنال مطلوب یک ورژن مستقیم از سیگنال ورودی فیلتر وفقی است.

زمانی که الگوریتم وفقی همگرا شود، آن‌گاه فیلتر یک مدل را برای سیگنال ورودی به نمایش می‌گذارد که این مدل می‌تواند به عنوان یک مدل پیش‌بینی مورد استفاده قرار گیرد. در تصویر زیر نمایی از یک سیستم پیش‌بینی خطی نشان داده شده است.

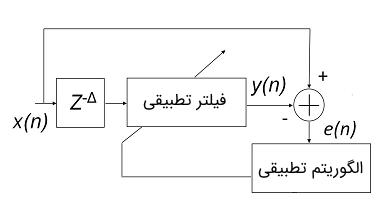
خروجی پیش‌بینی در این مدل بر اساس رابطه زیر بیان می‌شود:

$$y ( n ) = \sum _ { l = 0 } ^ { L − 1 } w _ 1 ( n ) x ( n − Δ − l)$$

در رابطه فوق، $$Δ$$ تعداد نمونه‌های تاخیر یافته است، بنابراین اگر از الگوریتم LMS استفاده کنیم، آن گاه ضرایب به صورت زیر آپدیت می‌شوند:

$$w ( n + 1 ) = w ( n ) + μ x ( n − Δ ) e ( n )$$

در رابطه فوق $$x ( n - ∆ )$$ برابر با بردار سیگنال مرجع تاخیر یافته است و به صورت زیر بیان می‌شود:

$$x ( n - ∆ ) = [ x ( n - ∆ ) x ( n - ∆ - 1 ) . . . x ( n - ∆ - L + l ) ] ^ T$$

همچنین $$e ( n ) = x ( n ) – y ( n )$$ برابر با خطای پیش‌بینی در نظر گرفته شده است.

انتخاب مناسب تاخیر پیش‌بینی $$∆$$ موجب بهبود عملکرد تخمین فرکانسی برای سینوسی‌های چندگانه در نویز سفید خواهد شد.

یک کاربرد بسیار متداول از پیش‌بینی کننده‌ها در کدگذاری پیش‌بین خطی سیگنال‌های گفتار است که در آن سیستم پیش‌بین، وظیفه تخمین پارامترهای گفتار را بر عهده دارد. این پارامترها بخشی از اطلاعات کدگذاری هستند که همراه با سایر مشخصه‌های سیگنال گفتار مانند تناوب ذخیره سازی و ... ارسال می‌شوند. پیش بین سیگنال وفقی در کاربرد ارتقای خط وفقی (Adaptive Line Enhancement) یا ALE نیز کاربرد دارد. در این کاربرد سیگنال ورودی، یک سیگنال با پهنای باند باریک است و به یک سیگنال با پهنای باند بزرگ افزوده می‌شود.

بعد از همگرا شدن، خروجی پیش بین، یک نسخه ارتقا یافته از سیگنال باند باریک خواهد بود. یک کاربرد دیگر از پیش بین‌های سیگنال، در توانایی فوق‌العاده آن‌ها در سرکوب کردن تداخلات باند باریک در یک سیگنال پهن باند است. در این حالت، سیگنال ورودی همان مشخصه‌های عمومی یک ALE را دارا است.

مدلسازی معکوس (Inverse Modeling) با فیلتر وفقی

مدلسازی معکوس را نیز می‌توان یکی دیگر از کاربردهای فیلتر وفقی به حساب آورد که در حوزه‌هایی مانند برابر کننده یا اکولایزرهای کانال مورد استفاده قرار می‌گیرند. فیلتر وفقی در این حالت به عنوان مثال در مودم‌ها برای کاهش اعوجاجات کانال بر اثر انتقال پر سرعت داده در یک کانال تلفنی به کار گرفته می‌شود. به منظور جبران سازی اعوجاجات کانال، نیاز است که از یک اکولایزر استفاده شود که معکوس تابع انتقال کانال باشد.

برای انتقال با سرعت بسیار بالای اطلاعات در طول یک کانال با اعوجاجات بسیار زیاد، می‌توان به چندین روش مختلف عمل کرد. یک راه این است که فیلترهای گیرنده و فرستنده را به صورتی طراحی کرد که ترکیب فیلتر و کانال منجر به یک مقدار خطای قابل قبول از مجموع نویز و تداخلات داخلی شود. راه دیگر برای رسیدن به این هدف، طراحی یک برابر کننده در سمت گیرنده است که با اعوجاجات کانال به صورت متقابل رفتار کند و آن‌ها را خنثی کند. توجه کنید که روش دوم نسبت به روش اول دارای کاربرد متداول‌تری در عملیات انتقال داده است

در تصویر زیر نمایی از یک اکولایزر یا برابر کننده کانال نشان داده شده است. سیگنال $$y ( n )$$ دریافت شده نسبت به سیگنال $$x ( n )$$ اصلی متفاوت است؛ زیرا این سیگنال توسط تابع انتقال کلی کانال یعنی $$C ( z )$$ دچار اعوجاج شده است. توجه کنید که این تابع انتقال فیلتر فرستنده، واسط انتقال و فیلتر گیرنده را شامل می‌شود.

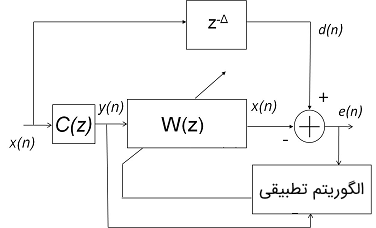
برای بازیابی سیگنال اصلی $$x ( n )$$ باید سیگنال $$y ( n )$$ توسط اکولایزر $$W ( z )$$ پردازش شود. $$W ( z )$$ دقیقا معکوس تابع انتقال کانال یعنی $$C ( z )$$ است و هدف این طراحی، جبران کردن اعوجاجات کانال در نظر گرفته شده است. بنابراین، اکولایزر باید توسط رابطه زیر طراحی شود:

$$W ( z )= \frac { 1 } { C ( z ) }$$

در عمل، یک کانال تلفنی متغیر با زمان است و به دلیل تغییرات در واسط انتقال، در مرحله طراحی به صورت ناشناخته در نظر گرفته می‌شود. بنابراین، به یک اکولایزر وفقی نیاز است که یک جبران سازی دقیق را در طول یک کانال متغیر با زمان فراهم کند. فیلتر وفقی به سیگنال مطلوب $$d ( n )$$ نیاز دارد تا بدین وسیله سیگنال خطای $$e ( n )$$ را برای الگوریتم LMS محاسبه کند.

ورژن تاخیر یافته سیگنال انتقالی یعنی $$x (n - Δ )$$، یک پاسخ مطلوب برای اکولایزر وفقی $$W ( z )$$ محسوب می‌شود. به این دلیل که فیلتر وفقی در سمت گیرنده واقع شده است، سیگنال مطلوبی که توسط فرستنده تولید می‌شود، در سمت گیرنده در اختیار نیست. سیگنال مطلوب ممکن است به صورت محلی در گیرنده با استفاده از دو روش تولید شود. در طول مرحله آموزش، ضرایب اکولایزر وفقی از طریق مبادله رشته‌های آموزش (Training Sequence) کوتاهی تنظیم می‌شوند. این رشته آموزش در گیرنده نیز تولید می‌شود و به عنوان سیگنال مطلوب $$d ( n )$$ برای الگوریتم LMS مورد استفاده قرار می‌گیرد.

پس از یک دوره آموزش کوتاه، فرستنده شروع به ارسال رشته داده می‌کند. در مود داده، خروجی اکولایزر $$x ( n )$$ توسط یه بخش تصمیم گیرنده (Decision Device) مورد استفاده قرار می‌گیرد تا داده‌های باینری تولید شود. فرض کنید که خروجی بخش تصمیم گیرنده صحیح باشد، آن گاه رشته باینری می‌تواند به عنوان سیگنال مطلوب $$d ( n )$$ مورد استفاده قرار گیرد و سیگنال خطای $$e ( n )$$ را برای الگوریتم LMS فراهم کند.

کاربرد فیلتر وفقی در سرکوب‌ اختلال (Jammer Suppression)

یک فیلتر وفقی می‌تواند یک ابزار بسیار قوی در سرکوب تداخلات باند باریک موجود در یک «گیرنده طیف گسترده رشته مستقیم» (Direct Sequence Spread Spectrum Receiver) باشد.

در شکل زیر نمایی از یک سیستم حذف اختلال نشان داده شده است.

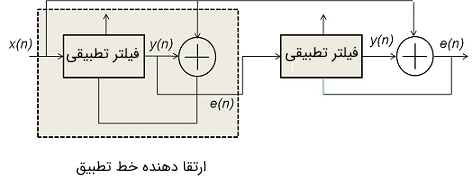
در این سیستم، خروجی فیلتر $$y ( n )$$ یک تقریب از اختلال است. این سیگنال، سپس از سیگنال دریافتی $$x ( n )$$ کاسته می‌شود تا تقریبی از طیف گسترده به دست آید. برای ارتقای عملکرد سیستم، معمولا از یک سیستم حذف اختلال دو طبقه استفاده می‌شود. یک ارتقا دهنده خط وفقی، که یک فیلتر وفقی دیگر است، با تاثیر «وابستگی محدود» (Finite Correlation) مقابله می‌کند. وجود وابستگی محدود منجر به این امر می‌شود که سیگنال مطلوب تا حدی از بین برود. تعداد ضرایبی که برای طراحی هر یک از فیلترها مورد نیاز است، در حد متوسط است، اما فرکانس نمونه‌برداری ممکن است تا مقادیر بسیار بالاتر از ۴۰۰ کیلو هرتز نیز در نظر گرفته شود.

فیلتر شکافی وفقی (Adaptive Notch Filter)

در مواقع خاص، سیگنال ورودی اولیه یک سیگنال پهن باند است که توسط تداخلات ناخواسته باند باریک سینوسی خراب (Corrupted) شده است. روش متداول برای از بین بردن این اختلالات سینوسی، استفاده از یک فیلتر شکافی است که در فرکانس اختلالات تنظیم شده باشد. اما برای طراحی فیلتر، به مقدار فرکانس دقیق اختلال نیاز داریم. یک فیلتر شکافی وفقی، این توانایی را دارد که فرکانس تداخلات را به صورت دقیق دنبال کند. به همین دلیل این نوع از فیلترها مخصوصا در مواقعی که تداخل سینوسی در فرکانس دچار تغییر می‌شود، بسیار مورد استفاده قرار می‌گیرند.

یک فیلتر شکافی وفقی تک فرکانسی با دو وزن وفقی در تصویر زیر نشان داده شده است.

در این فیلتر شکافی وفقی سیگنال ورودی، یک سیگنال کسینوسی با رابطه زیر است:

$$x ( n ) = x _ 0 ( n ) A c o s ( ω _ o n )$$

از یک شیفت دهنده فاز ۹۰ درجه استفاده می‌شود تا سیگنال تربیعی زیر به دست آید:

$$x _ 1 ( n ) = A s i n ( ω _ 0 n )$$

برای یک سیگنال سینوسی، به دو ضریب فیلتر وفقی نیاز است. ورودی مرجع به این دلیل مورد استفاده قرار می‌گیرد که مولفه سینوسی موجود در سیگنال ورودی اولیه $$d ( n )$$ تخمین زده شود. فرکانس مرکزی یک فیلتر شکافی برابر با فرکانس مرکزی سیگنال نویز سینوسی اولیه قرار داده می‌شود. بنابراین نویز در آن مقدار فرکانس تضعیف خواهد شد. این فیلتر شکافی وفقی یک روش بسیار ساده برای حذف تداخلات سینوسی به شمار می‌آید.

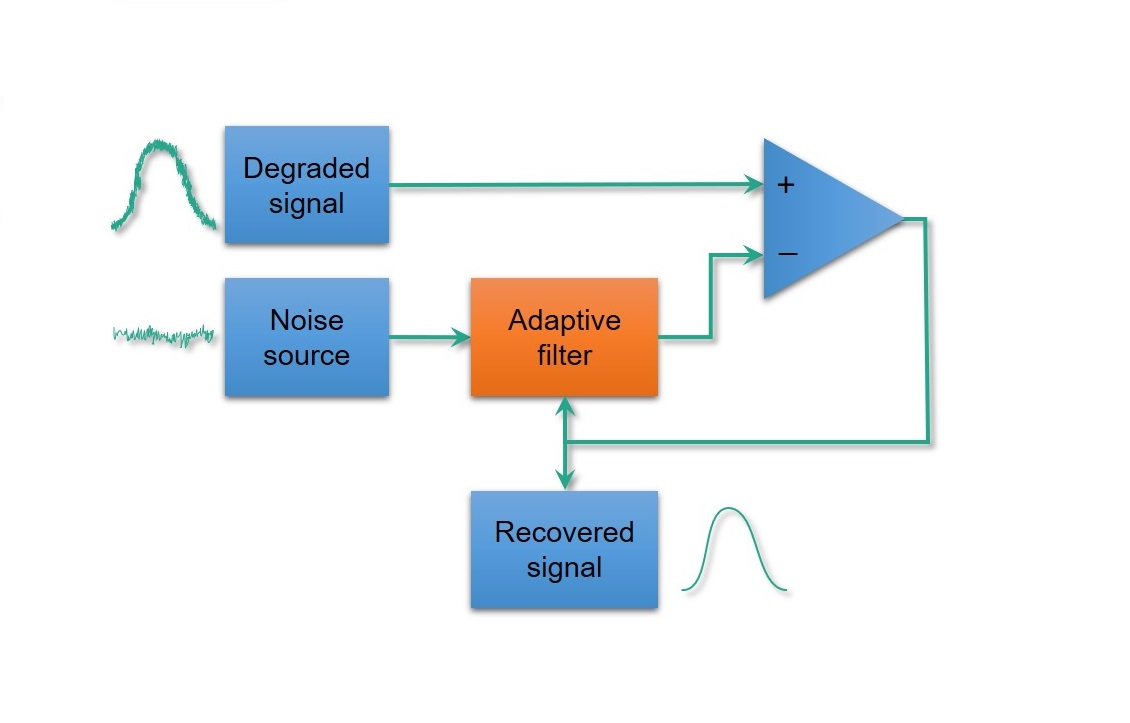
حذف نویز (Noise Canceller)

از سیستم‌های حذف نویز به منظور سرکوب کردن شدت نویزهای موجود در پس زمینه استفاده می‌شود. این پیکربندی در تلفن‌های همراه و مخابرات رادیویی به کار گرفته می‌شود؛ زیرا این وسایل گاهی در شرایطی استفاده می‌شوند که در محیط نویز بسیار زیادی وجود دارد. در تصویر زیر یک سیستم حذف نویز وفقی نشان داده شده است.

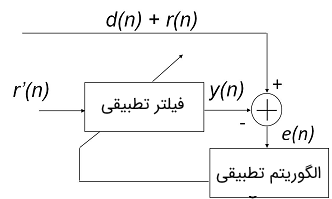
در سیستم حذف نویز بالا، بلوک حذف کننده از یک میکروفن جهت‌دار استفاده می‌کند تا بتواند دامنه لحظه‌ای نویزهای محیط یا $$r’ ( n )$$ را تخمین بزند و اندازه‌گیری کند. همچنین یک میکروفون دیگر برای دریافت سیگنال‌های گفتاری که شامل نویز هستند ($$d ( n ) + r ( n )$$) مورد استفاده قرار می‌گیرد.

نویز محیط توسط فیلتر وفقی پردازش می‌شود تا آن را برابر با مقدار نویز موجود در سیگنال گفتار قرار دهد. سپس این مقدار نویز از سیگنال گفتار تفریق می‌شود تا نویز در سیگنال مطلوب ما حذف شود. برای عملکرد موثرتر، نویز محیط باید با نویز موجود در سیگنال گفتار تا حد زیادی وابستگی داشته باشد.

در این حالت، اگر به مقادیر لحظه‌ای نویز آلوده کننده دسترسی نداشته باشیم، نمی‌توانیم نویز را سرکوب کنیم، اما می‌توانیم مقدار آن را با استفاده از ویژگی‌های آماری سیگنال و پردازش نویز کاهش دهیم. در تصویر زیر نمایی از یک سیگنال صوتی همراه با نویز نشان داده شده است.

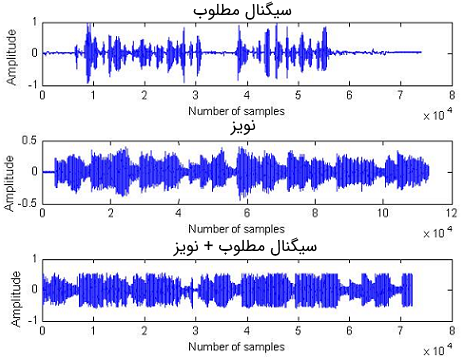
این سیگنال‌ها در یک سیستم حذف نویز مورد استفاده قرار گرفته‌اند که روی یک پردازنده سیگنال دیجیتالی به صورت عملی پیاده سازی شده است. سیگنال مطلوب یک سیگنال صوتی تک آوا است که فرکانس نمونه برداری آن ۸ کیلو هرتز در نظر گرفته شده است. سیگنال نویز یک قطعه موسیقی تک آوایی نامطلوب است که فرکانس نمونه برداری از آن برابر با ۱۱ کیلو هرتز است.

همان طور که در تصویر فوق دیده می‌شود سیگنال مطلوب تا حد بسیار زیادی حاوی نویز موسیقی است. بنابراین در این ساختار باید از یک الگوریتم وفقی بسیار سریع استفاده شود تا سیستم به سرعت همگرا شود و تمام المان‌های نامطلوب را از سیگنال مطلوب حذف کند. در تصویر زیر آنالیز فرکانسی سیگنال‌هایی نشان داده شده است که در سیستم حذف نویز مورد استفاده قرار گرفته‌اند.

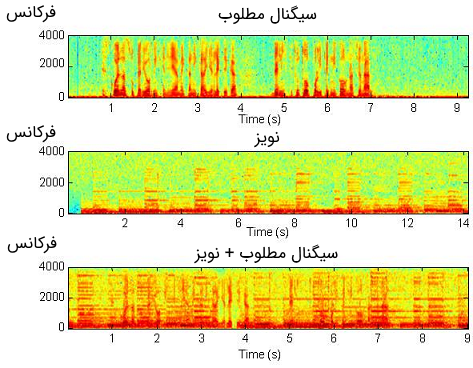
با توجه به تصویر فوق، سیگنال خروجی نسبت به سیگنال ورودی شامل برخی مولفه‌های فرکانسی اضافی است. خروجی سیستم حذف نویز یک سیگنال خطا است. در تصویر زیر سیگنال خطای به دست آمده هنگام استفاده از الگوریتم LMS نشان داده شده است.

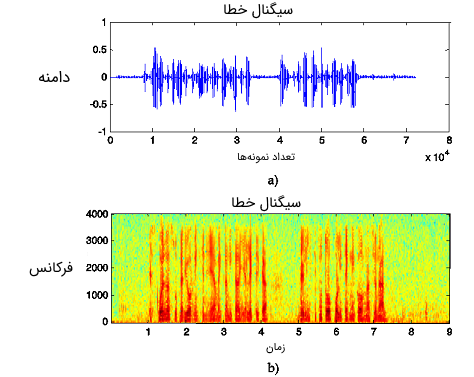
با توجه به نمودار طیفی فوق، می‌توان به این امر پی برد که تمام مولفه‌های فرکانسی نامطلوب در سیگنال حذف شده‌اند. سیستم حذف نویز وفقی در بسیاری از کاربردهای «کنترل نویز فعال» (Active Noise Control) یا ANC مورد استفاده قرار می‌گیرد. مثلا در هواپیماها برای حذف کردن نویز فرکانس پایین درون کابینه و به منظور آسایش بیشتر مسافران از حذف نویز وفقی و کنترل نویز فعال استفاده می‌شود.

بسیاری از کارخانجات بزرگ هواپیماسازی چنین سیستم‌هایی را مخصوصا برای هواپیماهای پرسر و صدا و پروانه‌ای توسعه می‌دهند. همچنین در صنعت اتومبیل‌سازی، سیستم‌های کنترل نویز فعال به منظور کاهش نویز جاده طراحی می‌شوند و برای این کار از میکروفون‌ها و بلندگوهای جاسازی شده در زیر صندلی‌های سرنشینان استفاده می‌شود. کاربرد دیگر فیلترهای وفقی و سیستم‌های کنترل نویز فعال در صدا خفه کن اکتیو برای لوله اگزوز موتور است که مدت‌هاست در کمپرسورهای صنعتی و ژنراتورها مورد استفاده قرار می‌گیرد.

با کاهش قیمت سیستم‌های کنترل نویز فعال، در حال حاضر حتی کارخانجات اتومبیل‌سازی نیز سیستم صدا خفه کن اکتیو را جایگزین مناسبی برای انواع غیر فعال آن می‌دانند و در اکثر خودروهای نسل جدید خود از آن بهره می‌گیرند. نتیجه استفاده از یک سیستم کنترل نویز اکتیو علاوه بر آرامش سرنشین، کاهش فشار بازگشتی موتور است که انتظار می‌رود در یک سفر درون شهری ۵ تا ۶ درصد میزان مصرف سوخت را کاهش دهد.

کاربرد دیگر سیستم کنترل نویز فعال که موفقیت تجاری گسترده‌ای را به دست آورده است، درهدفون‌‌های فعال است که در آن‌ها نویزهای فرکانس پایین به صورت کامل حذف می‌شوند. هدفون‌های فعال مجهز به میکروفون‌هایی در بیرون از بدنه خود هستند که مقدار نویزی که توسط هدفون دریافت می‌شود را اندازه‌گیری می‌کنند. سپس این نویز از طریق ارسال سیگنال ضد نویز به بلندگوی هدفون خنثی می‌شود.

در سیستم کنترل نویز فعال، همچنین یک واحد میکروفون درون هر گوشی وجود دارد تا بر مقدار خطا نظارت داشته باشد و مقدار نویزی که توسط سیستم حذف نشده است را اندازه‌گیری کند و الگوریتم کنترل نویز فعال را بهینه‌سازی نماید. این کاربرد از سیستم‌های کنترل نویز فعال، در هدفون‌های خلبانی مخصوصا برای هلی کوپترهای پر سر و صدا و یا هواپیماهای پروانه‌ای بسیار ضروری است.

حذف اکو (Echo Cancellation)

در مخابرات، پدیده «اکو» (Echo) یا پژواک صدا می‌تواند شدیدا روی کیفیت و «قابل فهم بودن» (Intelligibility) مکالمات صوتی در تلفن، کنفرانس از راه دور و یا سیستم‌های ارتباطی تاثیر بگذارد. تاثیر درک شده از اکو، به دامنه و میزان تاخیر زمانی آن بستگی دارد. اما در حالت کلی، اکو با دامنه کافی و تاخیز مانی بیشتر از ۱ میلی ثانیه برای انسان قابل درک است.

حذف اکو، یکی از مهم‌ترین جنبه‌های طراحی یک سیستم مخابراتی مدرن مانند تلفن‌های متداول سیمی، تلفن‌های هندزفری، تلفن‌های موبایل سلولی و کنفرانس از راه دور به شمار می‌رود. در شبکه‌های انتقالی زمانی اکو به وجود می‌آید که یک ورژن تاخیر یافته و تضعیف شده از سیگنال توسط «منتشر کننده امواج الکترومغناطیسی» (Emitter) محلی به گیرنده راه دور ارسال و در آن جا دریافت شود.

سیگنال‌های اکو از ترانسفورمرهای هایبرید که تبدیل دو به چهار سیمی انجام می‌دهند، عدم تطابق امپدانس در طول خطوط دو سیمی و گاهی از تزویج آکوستیک بین بلندگو و میکروفون در مجموعه‌های مشترک ناشی می‌شوند. حذف اکو در مدلسازی‌های خود، این تزویج ناخواسته بین امیتر محلی و گیرنده را به حساب می‌آورد و یک سیگنال اکو مصنوعی را از اکوی حقیقی کسر می‌کند. بر اساس طبیعت سیگنال‌ها، سیستم به عنوان حذف اکو داده و یا حذف اکو صدا عمل می‌کند.

1. حذف اکو صدا (Voice Echo Canceller)

به دلیل مشخصه‌های سیگنال گفتار، سیستم حذف اکو صدا تا حدودی با سیستم حذف داده اکو متفاوت است. گفتار یک سیگنال به شدت غیر ایستا است و به دلیل پهنای باند و سرعت امواج آکوستیک در فضای باز، فیلتر باید دارای ضرایب بسیار طولانی باشد. همچنین به منظور رسیدن به یک عملکرد سطح بالا و پاسخ دادن به نیازهای کاربران، سیستم حذف اکو صدا ممکن است کاربردهای بسیار متنوعی از جمله در شناسایی گفتار و نویزگیری داشته باشد. در تصویر زیر، نحوه عملکرد یک سیستم حذف اکو صدا وفقی نشان داده شده است.

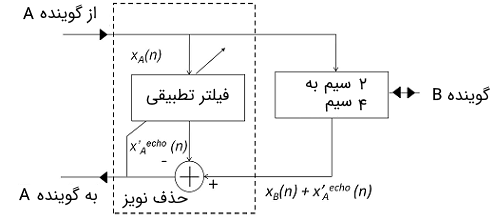
سیگنال گفتار از گوینده A به گوینده B یک ورودی برای هایبرید B دو به چهار سیمی و نیز سیستم حذف نویز محسوب می‌شود. سیستم حذف نویز سیگنال‌ها را از B تا A مانیتور می‌کند و تلاش می‌کند تا مسیر اکو را مدلسازی و یک کپی از اکو گوینده A را تجزیه کند. این کپی برای کسر کردن از سیگنال اصلی و حذف اکو از گوینده A در مسیر گوینده A به گوینده B مورد استفاده قرار می‌گیرد. سیستم حذف اکو در اصل یه فیلتر وفقی خطی است. ضرایب فیلتر به نحوی تطبیق پیدا می‌کنند که انرژی سیگنال روی خط در مقدار کمینه باشد.

فرض کنید که سیگنال روی خط از گوینده A به گوینده B برابر با $$y ـ B ( n )$$ باشد. این سیگنال از گفتار گوینده B یعنی $$x ـ B ( n )$$ به علاوه پالس اکو گوینده A یعنی $$x _ A ^ { e c h o } ( n )$$ تشکیل شده است. در نتیجه داریم:

$$y _ B ( n ) = x _ B ( n ) + x ^ { e c h o } _A ( n )$$

سیگنال گفتار و نیز سیگنال اکو به صورت همزمان روی خط تلفن حضور نمی‌یابند، مگر در حالتی که هر دو گوینده با هم شروع به حرف زدن کنند. فرض کنید که پاسخ ضربه کوتاه شده مسیر اکو با یک فیلتر FIR مدل شده باشد. در این شرایط، تخمین خروجی سیگنال اکو سنتز شده می‌تواند به صورت زیر بیان شود:

$$x ^ { ' \; e c h o } _ A ( n ) = \sum _ { l = 0 } ^ P h _ l ( n ) x _ A ( n − l )$$

در رابطه فوق، $$h _ l ( n )$$ برابر با ضرایب متغیر با زمان مدل فیلتر FIR وفقی مسیر اکو و $$x ^ { ' \; e c h o } _ A ( n )$$ برابر با تخمینی از مقدار اکو گوینده A روی خط از گوینده B به گوینده A است. سیگنال اکو مانده یا مقدار سیگنال خطا، بعد از تفاضل سیگنال اکو بر اساس رابطه زیر به دست می‌آید:

$$e ( n ) = y _ B ( n ) − x ^ { ' \; e c h o } _A ( n ) = x _ B ( n ) + x ^ {e c h o } _ A ( n ) − \sum _ { l = 0 } ^ P h _ l ( n ) x _ A ( n − l )$$

برای لحظاتی از زمان که گوینده A در حال حرف زدن است و گوینده B گوش می‌دهد، سیگنال اکو فقط از خط B به A وجود دارد. در نتیجه داریم:

$$e ( m ) = x ^ { ' \; e c h o } _A ( n ) =x ^ {e c h o } _ A ( n ) − x ^ { ' \; e c h o } _A ( n ) = x ^ {e c h o } _ A ( n ) − \sum _ { l = 0 } ^ P h _ l ( n ) x _ A ( n − l )$$

در رابطه فوق، $$x ^ { ' \; e c h o } _A ( n )$$ برابر با سیگنال مانده یا سیگنال خطا است.

گاهی در برخی مواقع ممکن است اتفاق بیفتد که دو گوینده با هم شروع به حرف زدن کنند. در واقع در این حالت (Double Talk)، دو گوینده به صورت همزمان حرف می‌زنند و «انتقال دو جهته» (Bidirectional Transmission) رخ می‌دهد. در هنگام انتقال دو جهته، «ناهماهنگی» (misalignment) بین ضرایب اتفاق می‌افتد و در تضعیف سیگنال اکو مشکل پیش می‌آید. یک راه برای حل این مشکل این است که ضرایب هنگام Double Talk ثابت حفظ شوند. اما برای انجام این کار نیاز است که ابتدا حرف زدن همزمان توسط سیستم تشخیص داده شود. عملکرد یک سیستم تشخیص Double Talk برای ایجاد مکالمات با کیفیت امری ضروری محسوب می‌شود.

۲. حذف اکو داده (Data Echo Canceller)

پیچیدگی سیستم‌های حذف اکو با افزایش تجمیع سیستم‌های تلفن سیمی و سیستم‌های سلولی موبایل، هر روز پیچیده‌تر می‌شود. به همین دلیل استفاده از روش‌های تبادلات دیجیتال، مانند مود انتقال آسنکرون برای انتقال جامع داده، صدا و تصویر در حال پیشرفت است. این سیستم‌ها از «سیگنال‌های داده انتقال تمام مضاعف» (Full Duplex Transmission Data Signals) استفاده می‌کنند و به صورت همزمان سیگنال‌ها در دو جهت و در یک باند فرکانسی منتقل می‌شوند. در حالی که در انتقال نیم مضاعف، در هر لحظه فقط از انتقال یک جهته استفاده می‌شود. اصول کاری انتقال داده تمام مضاعف در تصویر زیر نشان داده شده است.

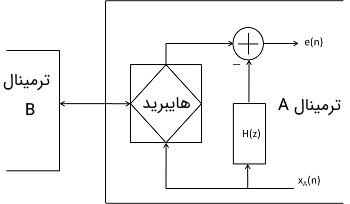
سیگنال $$x _ A ( N )$$ از ترمینال A به ترمینال B توسط یک خط دو سیمی منتقل می‌شود. سیگنال $$y ( n )$$ در ورودی گیرنده ترمینال A از دو مولفه تشکیل شده است، یک سیگنال از ترمینال B یا $$y _ B ( n )$$ که سیگنال اطلاعات مفید است و مولفه دوم، اکو بازگشتی نامطلوب است که از سیگنال $$x _ A ( n )$$ تولید می‌شود. $$H ( z )$$ یک فیلتر است که می‌خواهد سیگنال اکو سنتز شده $$y ^ { ' } ( n )$$ را تولید کند که تا حد ممکن به $$x _ A ( N )$$ نزدیک باشد و بعد از تفاضل، مقدار خطای خروجی $$e ( n )$$ به اندازه کافی نزدیک به $$y _ B ( n )$$ حفظ شود تا به این طریق انتقال داده از ترمینال B به ترمینال A مورد رضایت باشد.

تعداد ضرایب فیلتر وفقی (N) با توجه به طول پاسخ ضربه سیگنال اکو تعیین می‌شود که باید جبران شود و فرکانس نمونه برداری نیز برای این کار باید مورد توجه قرار گیرد. به منظور محاسبه تعداد ضرایب، می‌توان از رابطه زیر استفاده کرد:

$$N = ( 2 D / v ) f _ s$$

در رابطه فوق، $$N$$ برابر با تعداد ضرایب فیلتر وفقی، $$D$$ برابر با طول خط و $$v$$ برابر با سرعت سیگنال الکتریکی در طول خط مشترک است. همچنین $$f _ s$$ برابر با فرکانس نمونه برداری در نظر گرفته شده است. از آن جا که مشخصه‌های خط انتقال متناسب با زمان ممکن است تغییر کند، پیاده‌سازی یک فیلتر وفقی امری ضروری است.

۳. حذف اکو آکوستیک (Acoustic Echo)

اکو آکوستیک از مسیر فیدبک تنظیم شده بین گوینده و میکروفون ناشی می‌شود و در تلفن‌های موبایل، تلفن‌های هندزفری و یا کنفرانس از راه دور و سمعک مشاهده می‌شود. اکوی آکوستیک از سطوح چندگانه مختلف مانند دیوار، سقف و کف منعکس می‌شود و در مسیرهای مختلف منتشر می‌شود. اگر مقدار تاخیر زمانی زیاد بزرگ نباشد، آن گاه ممکن است سیگنال اکو آکوستیک را به صورت یک «طنین» (Reverberation) نرم درک کنیم که ممکن است با کیفیت ممتاز صدا در مکان‌هایی مانند سالن‌های کنسرت جمع شود. یک مشخصه طنین مطلوب می‌تواند کیفیت اجرای موسیقی را بالا ببرد.

اکو آکوستیک می‌تواند از ترکیبی از تزویج‌های آکوستیک مستقیم و تاثیر چند مسیری (Multipath Effect) در مکان‌هایی ناشی شود که سیگنال صوتی از سطوح مختلف منعکس می‌شود و سپس توسط میکروفن دریافت می‌شود. در بدترین شرایط، فیدبک آکوستیک می‌تواند منجر به ایجاد یک صدای جیغ مانند شود. این اتفاق زمانی رخ می‌دهد که مقدار کافی از انرژی صوت ارسال شده توسط بلندگو، در میکروفون دریافت شود و در حلقه فیدبک به گردش در آید.

موثرترین روش حذف فیدبک آکوستیک، استفاده از سیستم حذف فیدبک وفقی یا AFC است. در تصویر زیر یک مدل از محیط فیدبک آکوستیک نشان داده شده است که از میکروفون، بلندگو و فضای طنین انداز یک اتاق تشکیل شده است.

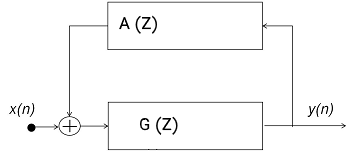
تابع اتقال Z مربوط به مدل خطی یک محیط فیدبک آکوستیک را می‌توان به صورت زیر بیان کرد:

$$H ( z ) = \frac { G ( z ) } {1 − G ( z ) A ( z ) }$$

در این رابطه، $$G ( Z)$$  برابر با مدل تابع انتقال z سیستم بلندگو و میکروفون و $$A ( Z )$$ مدل تابع انتقال z طنین و انعکاس چند مسیره محیط اتاق است. حال فرض کنید که سیستم ترکیبی میکروفون و بلندگو دارای یک پاسخ فرکانسی مسطح با بهره G است.

در نتیجه معادله را می‌توان به صورت زیر ساده سازی کرد:

$$H ( z ) = \frac { G } {1 − G A ( z ) }$$

به دلیل مشخصه طنین اتاق، مسیر فیدبک آکوستیک $$A ( Z )$$ خود یک سیستم فیدبک خواهد بود. مشخصه طنین یک محیط آکوستیک را شاید بتوان با یک مدل پیش‌بین خطی تمام قطب و یا یک مدل FIR نسبتا طولانی مدل کرد. معادله متناظر با رابطه ورودی خروجی در حوزه زمان برای یک مدل فیلتر خطی توسط رابطه زیر نوشته می‌شود:

$$y ( n ) = \sum_ {l = 0 } ^ P a _ l ( n ) y ( n − l ) + G _ x ( n)$$

در این رابطه، $$a _ l ( n )$$ ضرایب مربوط به یک مدل فیدبک خطی تمام قطب از محیط اتاق دارای طنین، $$G$$ فاکتور بهره دامنه میکروفون و بلندگو و $$x ( n )$$ و $$y ( n )$$ سیگنال‌های ورودی و خروجی حوزه زمان مربوط به سیستم میکروفون و بلندگو است.

موفق‌ترین سیستم کنترل فیدبک آکوستیک، مبتنی بر تخمین و حذف وفقی سیگنال فیدبک ساخته شده است. همانند سیستم حذف اکو خط، یک سیستم حذف فیدبک آکوستیک وفقی نیز در تلاش است تا یک کپی از فیدبک آکوستیک را سنتز کند. البته به چند دلیل مسئله حذف اکو آکوستیک از مسئله حذف اکو خط پیچیده‌تر است. اولین دلیل این است که اکو آکوستیک همیشه بسیار طولانی‌تر از اکوی خط تلفن زمینی است. در واقع، تاخیر زمانی یک سیگنال اکو آکوستیک بیشتر شبیه به اکو خط یک سیستم ماهواره‌ای جغرافیایی است.

تاخیر بزرگ یک مسیر اکو آکوستیک بر این امر دلالت دارد که ممکن است به فیلترهای بزرگ غیر عملی از مرتبه ضرایب چند هزار نیاز داشته باشیم. یکی از مهم‌ترین کاربردهای حذف فیدبک آکوستیک در سمعک است.

۴. حذف اکو چند ورودی - چند خروجی (MIMO)

سیستم حذف نویز MIMO در سیستم‌های کنفرانس از راه دور استریوفونیک یا چند آوایی و سالن‌های کنفرانس کاربرد دارد. سیستم‌های حذف اکو استریوفونیک نسبتا جدید هستند و موضوع بسیاری از تحقیقات در حال حاضر به شمار می‌آیند. در یک سیستم MIMO، تعداد P گوینده و Q میکروفون در یک اتاق وجود دارند. به این دلیل که یک مسیر فیدبک آکوستیک بین هر گوینده و میکروفون وجود دارد، در نتیجه در مجموع  P * Q مسیر فیدبک آکوستیک ایجاد شده است که نیاز به مدلسازی و تخمین دارند.

پاسخ ضربه قطع شده هر مسیر آکوستیک از بلندگوی i به میکروفون j توسط یک فیلتر پاسخ ضربه محدود $$h _ { i j }$$ مدلسازی می‌شود. همچنین پاسخ ضربه قطع شده هر مسیر آکوستیک از گوینده انسانی i به میکروفون j توسط یک فیلتر پاسخ ضربه محدود $$g _ { i j }$$ مدلسازی می‌شود. برای تعداد زیاد گوینده‌ها و میکروفون‌ها، مدلسازی و شناسایی کانال‌های آکوستیک متعدد تبدیل به یک مشکل بزرگ می‌شود. این اتفاق به دلیل وابستگی (Correlations) سیگنال‌های اکو از یک منبع مشترک و انتشار از طریق کانال‌های مختلف به وجود می‌آید.

حذف فیدبک وفقی

پردازنده‌های سمعک‌ها معمولا سیگنال ورودی را تقویت می‌کنند تا مقدار ضعف شنوایی را در کاربر جبران کنند. زمانی که این عمل تقویت کنندگی بزرگ‌تر از مقدار تضعیف مسیر فیدبک باشد، سیستم ناپایدار می‌شود و منجر به صدای سوت کشیدن (Whistling) در سمعک می‌شود که این امر مقدار بیشینه بهره‌ای که می‌توان به آن رسید را محدود می‌کند.

فیدبک آکوستیک در سمعک‌ها به تزویج صوتی بین بلندگو (یا گیرنده) و میکروفون این تجهیزات اشاره دارد. به دلیل این تزویج، سمعک‌ها در سیگنال مطلوب اعوجاج بسیار شدیدی را ایجاد می‌کنند و زمانی که بهره افزایش یابد، یک صدای جیغ آزار دهنده شنیده می‌شود. اگر تابع انتقال فیدبک در دست بود، می‌توانست به صورت سخت افزاری جبران شود. اما مشکل اصلی در اینجا دینامیک متغیر با زمان است که توسط تغییر در مشخصه‌های تداخل به وجود می‌آید. برخی دلایل محتمل ایجاد تغییر در دینامیک، بغل کردن و یا نزدیک شدن اشیایی مانند تلفن به گوش است.

تکنیک‌های متنوعی برای کاهش اثر منفی به وجود آمده توسط فیدبک آکوستیک وجود دارد. این تکنیک‌ها معمولا به دو دسته «سرکوب مسیر مستقیم» (Feedforward Suppression) و «سرکوب مسیر فیدبک» (Feedback Cancellation) دسته بندی می‌شوند. در تکنیک‌های سرکوب مسیر مستقیم، مسیر پردازش سیگنال معین مربوط به سمعک به نحوی اصلاح می‌شود که در هماهنگی با مسیر فیدبک پایدار باشد.

متداول‌ترین تکنیک، استفاده از یک فیلتر شکافی است. در یک فیلتر شکافی، هنگام وقوع فیدبک، بهره در یک باند فرکانسی باریک اطراف فرکانس بحرانی کاهش می‌یابد. با این حال، تکنیک‌های سرکوب مسیر مستقیم همگی پاسخ فرکانسی اساسی سمعک را اصلاح می‌کنند و به همین دلیل ممکن است به صورت جدی بر کیفیت صدا تاثیر بگذارند. بنابراین یک راه مناسب‌تر برای مشکل فیدبک آکوستیک، استفاده از تکنیک‌های حذف فیدبک به شمار می‌آید. در تصویر زیر نمایی از یک سیستم حذف فیدبک وفقی نشان داده شده است.

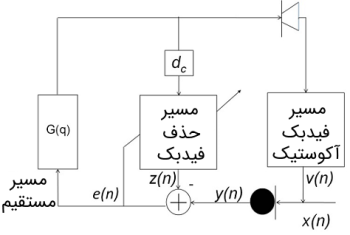
در این سیستم یک سیگنال تقریب $$z ( n )$$ از سیگنال فیدبک $$v ( n )$$ تولید می‌شود و سپس مقدار سیگنال تقریبی از سیگنال میکروفون کسر می‌شود تا در نهایت و در حالت ایده‌آل، فقط سیگنال مطلوب در ورودی مسیر فیدبک حفظ شود. از آن جا که مسیر آکوستیک بین بلندگو و میکروفون می‌تواند تا حد زیادی به محیط آکوستیک وابستگی داشته باشد، حذف کننده فیدبک باید وفقی باشد. زمانی که سیگنال ورودی خارجی به سیگنال ورودی دریافت شده وابسته باشد، تخمین مسیر فیدبک دارای بایاس است. وجود مشکل بایاس منجر به ایجاد خطای مدلسازی بسیار بزرگ و حذف کردن سیگنال مطلوب می‌شود.

بهبود سیگنال‌های ECG جنین و حذف سیگنال ECG مادر

اطلاعات دریافت شده از جنین توسط الکتروکاردیوگرام (Electrocardiogram) یا ECG، مانند الگوی ضربان قلب، در ارزیابی وضعیت جنین قبل از تولد و در حین تولد بسیار موثر هستند. این سیگنال‌ها از طریق الکترودهایی که روی بدن مادر قرار داده می‌شوند به دست می‌آیند. اما مشکلی که وجود دارد این است که سیگنال‌ها در معرض آلودگی به یک نویز پس زمینه بسیار بزرگ ناشی از بدن مادر قرار دارند. این مشکل را نیز می‌توان به عنوان یک مسئله حذف نویز وفقی در نظر گرفت که در آن $$d ( n )$$ برابر با سیگنال‌های مطلوب ECG جنین است که توسط سیگنال‌های مادر $$r ( n )$$ به نویز آغشته شده است. در واقع این نویز را می‌توان یک نویز جمع شونده در نظر گرفت. بنابراین سیگنال ECG کلی که اندزه‌گیری شده است ($$MFECG ( n )$$) را می‌توان به صورت زیر بیان کرد:

$$MFECG ( n ) = d ( n ) + r ( n )$$

حال یک سیگنال ECG دیگر که فقط مربوط به مادر ($$MMECG ( n )$$) است را به عنوان سیگنال مرجع قرار می‌دهیم. این سیگنال با $$r ( n )$$ همبستگی دارد و با سیگنال $$d ( n )$$ ناهمبسته است. سیگنال $$MMECG ( n )$$ می‌تواند برای تخمین نویز $$r ( n )$$ از طریق کمینه کردن خطای میانگین مربعات مورد استفاده قرار گیرد. در تصویر زیر یک بلوک دیگرام از نحوه بهبود سیگنال‌های ECG جنین نشان داده شده است.

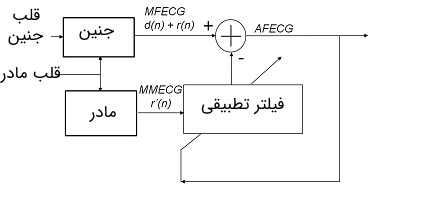
یک فیلتر وفقی برای تخمین مولفه‌های سیگنال مادر موجود در سیگنال ECG اندازه‌گیری شده جنین مورد استفاده قرار می‌گیرد و برای عملکرد خود از سیگنال ECG مادر کمک می‌گیرد. سپس مولفه‌های تخمین زده شده را از سیگنال $$MFECG ( n )$$ کسر می‌کنیم تا سیگنال فیلتر شده وفقی ECG جنین ($$AFECG$$) به دست آید که در آن مولفه‌های سیگنال مادر حذف شده است. سایر نویزها مانند انقباضات ماهیچه‌ای بدن مادر و حرکات جنین موجب دریفت پایه‌ای در MFECG در می‌شوند.

حذف نویز EOG از الکتروانسفالوگرام (Electroencephalogram) توسط فیلتر وفقی

زمانی که قرنیه مثبت و شبکیه چشم منفی باشد، چشم می‌تواند موجب ایجاد یک دوقطبی شود. هنگامی که چشم حرکت کند، میدان الکتریکی اطراف چشم تغییر می‌کند و یک سیگنال الکتریکی را به وجود می‌آورد که با نام الکتروکولوگرافی (Electrooculogram) یا EOG شناخته می‌شود. چون این سیگنال در جمجمه منتشر می‌شود، در نتیجه در سیگنال الکتروانسفالوگرام مغزی یا EEG به عنوان نویز دیده می‌شود و مشکلات جدی را برای تجزیه و تحلیل سیگنال EEG به وجود می‌آورد.

در حالت کلی دو نوع سیگنال EOG وجود دارد که باید حذف شوند. یکی از این سیگنال‌ها، آن‌هایی هستند که توسط حرکات عمودی چشم به وجود می‌آیند و VEOG نام دارند و نوع دوم سیگنال‌هایی هستند که توسط حرکات افقی چشم ایجاد می‌شوند و HEOG نام دارند. در نتیجه به صورت خلاصه می‌توان گفت که از دو سیگنال ورودی مرجع برای سیستم حذف نویز در این کاربرد استفاده می‌شود. در تصویر زیر نمایی از یک سیستم حذف نویز EOG نشان داده شده است.

سیگنال اولیه ورودی به این سیستم همان سیگنال EEG یا $$s ( n )$$ است که توسط الکترودهای مخصوصی ضبط می‌شود. این سیگنال به عنوان ترکیبی از EEG واقعی $$x ( n )$$ و مولفه نویز $$r ( n )$$ مدل می‌شود. $$v ( n )$$ و $$v ’ ( n )$$ به ترتیب به عنوان دو ورودی مرجع VEOG و HEOG در نظر گرفته می‌شوند. سیگنال‌های $$v ( n )$$ و $$v ’ ( n )$$ به صورتی ناشناخته با مولفه نویز $$r ( n )$$ در ورودی اولیه همبستگی دارند. سیگنال خروجی مطلوب از سیستم حذف نویز $$e ( n )$$، همان سیگنال صحیح یا تمیز EEG محسوب می‌شود.

کاربرد فیلتر حذف نویز وفقی در اندازه‌گیری الکتریکی AC

با استفاده از یک فیلتر حذف نویز وفقی می‌توان بازده یک اندازه‌گیری الکتریکی را بهبود بخشید. همیشه یک مدار اندازه‌گیری‌ AC، تحت تاثیر نویز ایجاد شده توسط بیم‌های فرکانسی خط قرار می‌گیرد. در تصویر زیر نمایی از یک سیستم برای حذف بیم‌های فرکانسی خط نشان داده شده است.

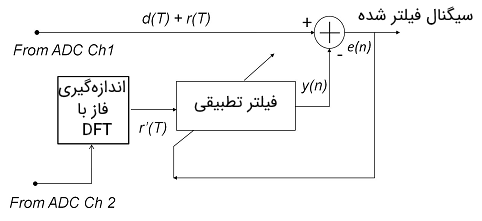
در مدار فوق، از یک مبدل آنالوگ به دیجیتال یا ADC برای نمونه‌برداری از ولتاژ خط استفاده می‌شود تا فاز نسبت به کانال سیگنال تعیین شود که خود توسط مدار ADC دوم مشخص می‌شود. داده‌های فاز به عنوان ورودی نویز به یک فیلتر حذف نویز وفقی مورد استفاده قرار می‌گیرند تا تاثیر روی داده خروجی تقویت‌کننده «هدایت متقابل« (Transconductance) حذف شود.

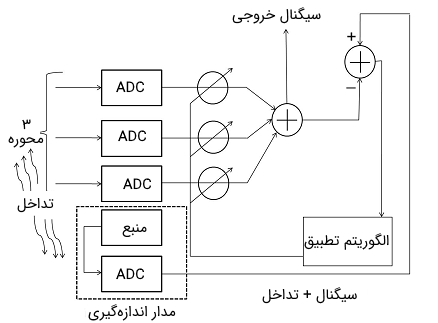
یک نوع متداول دیگر از تداخل در مدارات اندازه‌گیری AC، تزویج میدان مغناطیسی است که به وسیله منابع موجود در نزدیکی آن تولید می‌شود. در چنین شرایطی، ممکن است بتوان با استفاده از یک سیستم حذف تداخل وفقی با سیستم سیم‌پیچی ساده، میدان مغناطیسی محیط را به عنوان عامل به وجود آورنده تداخلات ناخواسته اندازه‌گیری کرد و سپس این تداخلات را از داده‌های به دست آمده از مدار اندازه‌گیر حذف کرد. همچنین در تصویر زیر نمایی از یک سنسور میدان مغناطیس ۳ محوره نشان داده شده است که به یک مبدل دیجیتال به آنالوگ یا ADC جداگانه متصل شده است. مدار ADC چهارم برای نمونه‌برداری از سیگنال به صورت همزمان با داده‌های ۳ محوره مورد استفاده قرار می‌گیرد.

اگر این مطلب برای شما مفید بوده است، مطالب و آموزش‌های زیر نیز برای مطالعه بیشتر به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های مهندسی برق
• آموزش الکترونیک ۳
• مجموعه آموزش‌‌های مهندسی مخابرات
• آموزش فیلترهای وفقی با الگوریتم LMS و RLS
• حلقه قفل فاز (PLL) چیست؟ — از صفر تا صد
• اسیلاتور کنترل شده با ولتاژ (VCO) — از صفر تا صد
• فیلتر میان گذر پسیو — از صفر تا صد

^^