ساده کردن عبارت های توان دار — آموزش به زبان ساده و با مثال
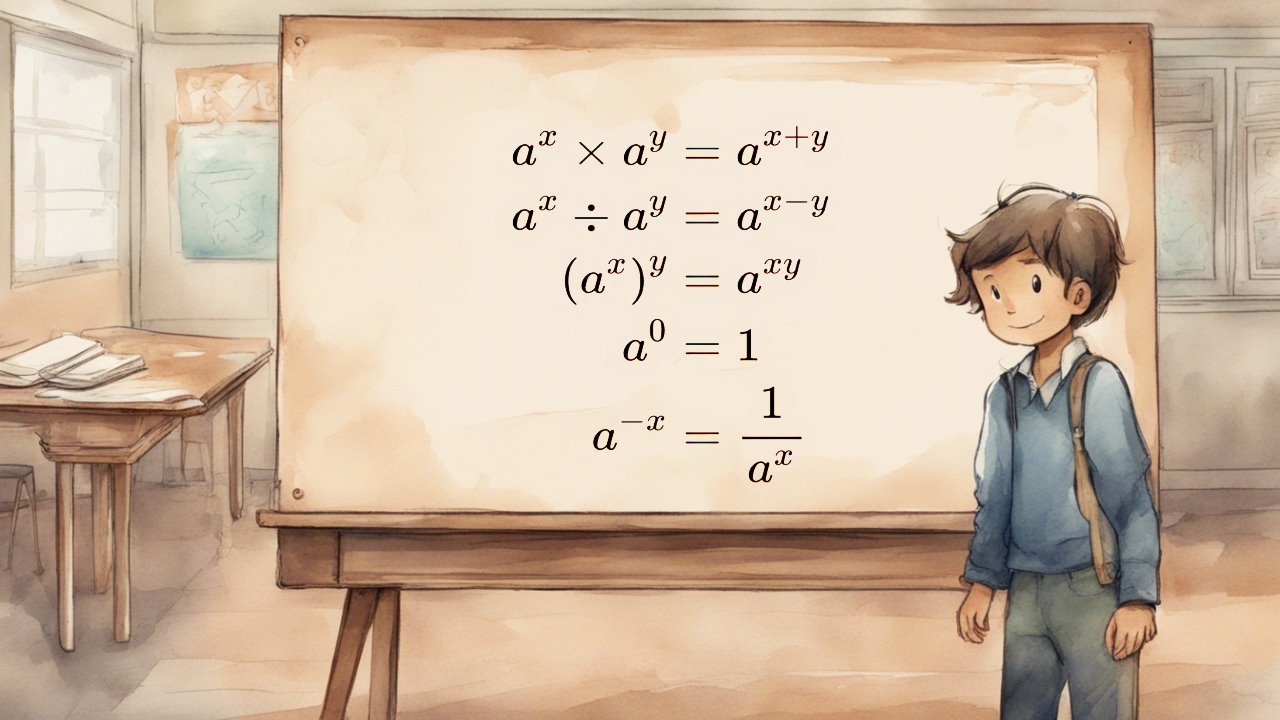
حتما در محاسبات خود با اعداد توان دار مواجه شدهاید. لازم است که عملیاتی که روی این گونه اعداد قابل اجرا است را بدانیم. هر چند میتوان اعداد توان دار را از حالت توانی خارج کرد و به صورت یک عدد معمولی نوشت، ولی استفاده از آنها، محاسبات را سادهتر کرده و خوانایی نتایج را بیشتر میکند. به همین جهت ساده کردن عبارت های توان دار برایمان اهمیت دارد. در نوشتارهای دیگر مجله فرادرس با نحوه ضرب و تقسیم اعداد توان دار آشنا شدید. همچنین نحوه جمع یا تفریق اعداد توان دار را هم فراگرفتیم.
در اینجا قرار است به کمک تجزیه یا ترکیب اعداد توان دار، عبارتها را ساده کردن و نمایش دهیم. حتما به یاد دارید که اعداد توان دار را به صورتی مینویسند که یک عدد در پایه و یک عدد در توان قرار میگیرد. البته با توجه به موضوع بحث ما، این اعداد ممکن است صحیح، گویا یا یکی از اعداد حقیقی باشند. به همین جهت و برای سادگی امر، اعداد صحیح را مبنا قرار داده ولی توجه داریم که به جای اعداد صحیح هر نوع عدد دیگری نیز میتواند قرار گیرد.
ساده کردن عبارت های توان دار
یک عدد توان دار به صورت زیر و به شکل پارامتری نمایش داده میشود که در آن $$a$$ را پایه و $$b$$ را توان یا نما میگویند.
$$ \large {\displaystyle a^b } $$
به این ترتیب مثالهای زیر همگی نشانگر اعداد توان دار هستند. میخواهیم با استفاده از روشهایی که معرفی میکنیم، ساده کردن عبارت های توان دار را به شکلی انجام دهیم که ضرب، تقسیم، جمع یا تفریق این گونه اعداد راحتتر محاسبه شوند.
$$ \large {\displaystyle 2^3 } \quad , \quad \large {\displaystyle 2^{ (-3)} } $$
$$ \large {\displaystyle (\dfrac{ 1}{ 2})^3 } \quad ,\quad \large {\displaystyle (\dfrac{ 1}{ 2})^{( -3)} } $$
$$ \large {\displaystyle 2^{ \frac{ 1}{ 3} }} \quad , \quad \large {\displaystyle (\dfrac{ 1}{ 2})^{ \frac{ 1}{ 3} } }$$
$$ \large {\displaystyle (0.01)^3 } \quad , \quad \large {\displaystyle ( 0.01)^{ \frac{ 1}{ 4} } }$$
$$ \large {\displaystyle (\sqrt{ 2})^{ \frac{ 1}{ 4} } } \quad , \quad \large {\displaystyle (\sqrt{ 2})^{ \frac{ 1}{ \sqrt{ 3}} } }$$
ولی چیزی که در این متن به آن خواهیم پرداخت، حالتهایی است که هم پایه و هم توان، اعداد گویا باشند. بنابراین، دو مورد آخر را نادیده میگیریم.

توجه دارید که اعداد اعشاری را میتوان به کمک روشهایی به کسر متعارفی تبدیل کرده و به شکل یک عدد گویا نمایش داد. برای مثال عدد $$0.01$$ به صورت کسری و به شکل $$\frac{1}{100}$$ قابل نمایش بوده که یک عدد گویا یا کسر متعارفی است.
از طرفی اگر توانهای یک عدد تواندار به صورت یک عدد کسری نوشته شود، میتوان آن عدد را به شکل رادیکال نوشت و قواعد رادیکال را برای ساده کردن اعداد توان دار مورد استفاده قرار داده و به کار بست. به رابطه زیر توجه کنید که در آن یک عبارت تواندار (با توان منفی) به صورت رادیکال درآمده است.
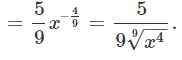
نمایش و ساده کردن عدد توان دار به صورت ضرب دو عدد توان دار دیگر
یادآوری میکنیم که در این متن، هم توان و هم پایه اعداد تواندار را از بین اعداد صحیح یا گویا در نظر میگیریم. با استفاده از قاعده ضرب و ارتباط آن با توان، مشخص است که هر عدد توان دار را میتوان به صورت ضرب دو عدد توان دار دیگر نوشت به شرطی که پایهها را یکسان در نظر بگیریم. به رابطه زیر دقت کنید.
$$ \large {\displaystyle a^{(n + m)} = a^m \times a^n } $$
برای مثال تساویهای زیر را نوشتهایم تا این نکته بهتر مشخص شود.
$$ \large {\displaystyle 6^5 = 6^{( 2 + 3)} = 6^2 \times 6^3 } $$
$$ \large {\displaystyle 6^5 = 6^{( 1 + 4)} = 6^1 \times 6^4 } $$
$$ \large {\displaystyle 6^5 = 6^{( -2 + 7)} = 6^{ (-2)} \times 6^7 } $$
همانطور که میبینید، $$6^5$$ را میتوان به چندین شیوه به صورت ضرب اعداد تواندار نوشت. بنابراین مشخص است که در این روش میتوانیم، تبدیل عدد توان دار را به صورتهای مختلف و با اعداد تواندار متفاوت نمایش دهیم. البته همانطور که دیدید، پایه همه این اعداد، برابر با ۶ بود. ولی حتی ممکن است که پایه را هم تغییر داده و به شکل دیگری اعداد توان دار را به صورت ضرب دو عدد تواندار نمایش داد. به مثالهایی که در ادامه آورده شده، توجه کنید.
$$ \large {\displaystyle 6^5 = 6^{( 2 + 3 )} = (\dfrac{ 1}{ 6})^{( -2)} \times 6^3 } $$
$$ \large {\displaystyle 6^5 = 6^{( 2 + 3 )} = (\dfrac{ 1}{ 6})^{( -2)} \times (\dfrac{ 1}{ 6})^{( -3)} } $$
$$ \large {\displaystyle 6^5 = 6^{( 2 + 3 )} = (\dfrac{ 1}{ 6})^{( -2)} \times (\dfrac{ 1}{ 6})^{( -3)} } $$
$$ \large {\displaystyle 6^5 = 6^{( 2 + 3 )} = (\dfrac{ 2}{ 12})^{( -2)} \times (\dfrac{ 3}{ 18})^{( -3)} } $$
در مثالهای بالا مشاهده کردید که حتی ممکن است پایهها نیز برابر نباشند. البته با تغییر و ساده کردن پایهها، ممکن است بتوان آنها را یکسان کرد. در ادامه متن به این گونه موارد که منجر به ساده کردن عبارت های توان دار میشود، نیز خواهیم پرداخت.
ساده کردن اعداد توان دار در تقسیم و ضرب
گاهی لازم است که عبارتها و اعداد توان دار به شکلی تجزیه کنیم که محاسبات و ساده کردن عبارت های توان دار بخصوص ضرب و تقسیم، آسانتر صورت گیرد. برای این منظور، به رابطه زیر دقت کنید. مشخص است که ابتدا توان را به صورت ضرب نمایش داده، سپس هر دو عبارت را در هم ضرب کردهایم.
$$ \large {\displaystyle ( a^m \times b^m ) = \overbrace{ a \times a \times \ldots \times a}^{ \text { m times} } \times \overbrace{ b \times b \times \ldots \times b}^\text { m times} = (a \times b )^m } $$
منظور از عبارت times در عبارت بالا، تعداد ضربها است. برای مثال m times به معنی m بار عمل ضرب است. به مثالهایی که در این زمینه معرفی کردهایم دقت کنید. همانطور که میبینید، حاصل ضربهایی که در سمت چپ قرار دارد، به شکل سادهتری در سمت راست محاسبه شدهاند.
$$ \large {\displaystyle 2^3 \times 3^ 3 = (2 \times 2 \times 2 ) \times ( 3 \times 3 \times 3) = ( 2 \times 3 ) \times ( 2 \times 3 ) \times ( 2 \times 3 ) = 6^3 } $$
$$ \large {\displaystyle 5^4 \times 2^4 = (2 \times 5)^4 = 10^4 = 10000} $$
$$ \large {\displaystyle 5^2 \times 2^3 = ( 5 \times 5 ) \times ( 2 \times 2 \times 3 ) = ( 5 \times 2) \times (5 \times 2) \times 2 = 2 \times 10^2 = 200} $$
$$ \large {\displaystyle 6^2 \div 2^3 = ( 6 \times 6 ) \div ( 2 \times 2 \times 2 ) = ( 6 \times 6) \div (2 \times 2) \times 2 = (\dfrac{ 6}{ 2} \times \dfrac{ 6}{ 2}) \times \dfrac{ 1}{ 2}= \dfrac{ 3^2}{ 2} = \dfrac{ 9}{ 2} = 4.5 } $$
همانطور که مشاهده کردید، گاهی با تجزیه هر یک از عاملهای ضرب یا تقسیم، محاسبات به سادگی صورت میگیرد. مثلا در آخرین تساوی که مطرح کردیم، توان دوم ۶ را به صورت ضرب دو عدد ۶ نوشتیم، همچنین توان سوم را با ۲ مشخص کردیم. از طرفی چون دوبار ۶ در هم ضرب شده و همین کار را برای ۲ نیز انجام دادیم. برای سادگی، ۶ را بر ۲ به صورت دو به دو بر هم تقسیم کردهایم. به تصویر زیر دقت کنید.
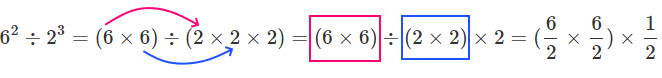
ساده کردن عبارت های توان دار پارامتری
این بار به جای اینکه از اعداد توان دار استفاده کنیم، عبارتهای پارامتری را که به صورت تواندار هستند، مبنای کار قرار میدهیم.

همان طور که در ابتدای متن اشاره کردیم، یک عبارت یا عدد توان دار به صورت پارامتری با ذکر پایه و نما مشخص میشود. حال فرض کنید که قرار است یک عبارت توان دار را در عبارت توان دار دیگری ضرب کنیم.
$$ \large {\displaystyle (x^2 + x y )( y^2 - x y) }$$
با توجه به عملگر ضرب که بین پرانتزها وجود دارد، ساده کردن عبارت های توان دار را انجام میدهیم. نتیجه به صورت زیر خواهد بود.
$$ \large {\displaystyle x^2 \times ( y^2 - x y) + x y \times ( y^2 - x y) }$$
$$ \large {\displaystyle (x^2 y^2 - x^3 y) + (x y^3 - (x y)^2 }$$
حالا ساده سازی کردن عبارت های توان دار که دارای پایه و نمای یکسان هستند را اجرا میکنیم. همانطور که میدانید، $$x^2 y^2 = (xy)^2$$، پس با ساده کردن به رابطه زیر خواهیم رسید.
$$ \large {\displaystyle ( x y )^2 - x^3 y + x y^3 - (x y)^2 }$$
واضح است که عبارت $$(x y )^2$$ از ابتدا و انتهای عبارت بالا، ساده و حذف میشود. نتیجه نهایی ساده کردن عبارت های توان دار در رابطه بالا، به صورت زیر قابل نمایش است.
$$ \large {\displaystyle - x^3 y + x y^3 = -( x y )( x^2 - y^2) }$$
به یک مثال دیگر در این زمینه توجه کنید. عبارت زیرا را در نظر بگیرید که تقسیم دو عبارت تواندار را نشان میدهد.
$$ \large {\displaystyle \left[ (35 x^3 y^4 ) \div (63 x^{ -4} y^7) \right]^2 }$$
ابتدا این تقسیم را به صورت کسری مینویسیم.
$$ \large {\displaystyle \left[ \dfrac{( 35 x^3 y^4 )} {(63 x^{ -4} y^7) } \right]^2 }$$
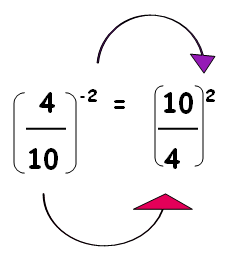
حال به کمک قاعده تقسیم برای جملات مشابه با پایههای یکسان، تقسیم را انجام میدهیم. به یاد دارید که در تقسیم، پایه مشترک نوشته شده و نمای مخرج از صورت کم میشود.
$$ \large {\displaystyle \left[ \dfrac{ 35}{ 63} \left( x^{ 3- ( -4)} \right) \left( y^{( 4 - 7)} \right) \right]^2 = \left[ \dfrac{ 35}{ 63} \left( x^{ 7} \right) \left( y^{( -3)} \right) \right]^2 }$$
در نتیجه پس از مربع کردن عبارت داخل پرانتز به نتیجه زیر خواهیم رسید.
$$ \large {\displaystyle \left( \dfrac{ 5}{ 9} \right)^2 \dfrac{ \left( x^{ 14} \right)}{ \left( y^{ 6} \right) } = \dfrac{ 25}{ 81} \dfrac{ x^{14} }{ y^6} }$$
توجه دارید که براساس قواعد اعداد تواندار، اگر عبارت توانداری به توان عدد دیگری برسد، پایه نوشته شده و توانها در هم ضرب میشوند.
خلاصه و نتیجهگیری
اعداد توان دار بخصوص در زمانی که با اعداد بسیار بزرگ یا بسیار کوچک سروکار داریم، به کار میروند. به جای آن که این گونه اعداد را به صورت یک عدد حسابی درآوریم، بهتر است محاسبات جمع و تفریق، ضرب و تقسیم و ساده کردن آنها را به شکلی که در این متن به آن اشاره کردیم، اجرا کنیم. نمایش نتیجه به صورت یک عدد توان دار نیز خوانایی و انجام عملیات بعدی را سادهتر خواهد کرد.
همانطور که خواندید، گاهی با فاکتورگیری یا گاهی با ترکیب عبارتها یا اعداد توان دار بهتر میتوان محاسبات را انجام داد. به یاد داشته باشید که یک چند جملهای، شکل خاصی از نمایش ارتباط بین اعداد و عبارت های توان دار است که به صورت پارامتری نمایش داده شده. بنابراین قواعدی که در مورد چند جملهای ها داریم، برای ساده کردن عبارت های توان دار قابل استفاده است.










