حل مسائل الکتریسیته ساکن – به زبان ساده

در این مطلب از مجله فرادرس قصد داریم به حل مسائل الکتریسیته ساکن بپردازیم. مسائل الکتریسیته ساکن به بررسی اثرات بارهای الکتریکی در حالت سکون می‌پردازند. انواع مختلفی از مسائل الکتریسیته ساکن بسته به داده‌ها و مجهولات مسئله وجود دارد. در الکتریسیته ساکن همواره میدان‌های الکتریکی برای بارهای ساکن محاسبه می‌شوند. با حرکت بارها جریان الکتریکی به وجود می‌آید و مسائل این حوزه به الکتریسیته جاری مربوط است.

روش حل مسائل الکتریسیته ساکن

برای حل مسائل الکتریسیته ساکن ابتدا پتانسیل الکتریکی محاسبه می‌شود. سپس شدت میدان الکتریکی و توزیع بار الکتریکی بر حسب پتانسیل به دست می‌آید. به طریق مشابه اگر توزیع بار معلوم باشد، می‌توان پتانسیل الکتریکی و شدت میدان الکتریکی را محاسبه کرد. در بسیاری از مسائل عملی، توزیع دقیق بار در همه نقاط را نمی‌دانیم. برای مثال،‌ اگر تعدادی بار نقطه‌ای و اجسام رسانا با پتانسیل معلوم داشته باشیم، محاسبه شدت میدان الکتریکی در فضا یا توزیع بارهای سطح روی اجسام هادی بسیار مشکل است. اگر اجسام هادی مرزهایی با هندسه ساده داشته باشند، می‌توان از روش تصاویر برای حل مسائل الکتریسیته ساکن استفاده کرد.

در انواع دیگری از مسائل، ممکن است پتانسیل همه اجسام هادی معلوم باشد و بخواهیم توزیع بارهای سطحی روی اجسام هادی و شدت میدان الکتریکی در محیط اطراف را بدانیم. در این سری مسائل، معادلات دیفرانسیل با شرایط مرزی مناسب آن حل می‌شود. به این مسائل، «مسائل مقدار مرزی» (Boundary Value Problems) گفته می‌شود. همچنین در حل مسائل الکتریسیته ساکن میدان‌های الکتریکی و مغناطیسی از طریق فرم‌های پیچیده‌تر معادلات ماکسول قابل محاسبه است.

معادله پواسون و معادله لاپلاس

در الکتریسیته ساکن دو معادله دیفرانسیل بنیادی وجود دارد. این معادلات در زیر آمده‌اند:

$$\large\nabla .D = \rho \, \, \, (C/m^3)$$

$$\large \nabla \times E =0$$

این دو رابطه، معادلات دیفرانسیل بنیادی برای حل مسائل الکتریسیته ساکن هستند و در محیط‌های مختلف قابل اعمال هستند. از آنجا که کرل میدان مغناطیسی صفر است، می‌توان گفت که این میدان، «غیر چرخشی» (Irrotational) است. بنابراین می‌توان یک پتانسیل الکتریکی اسکالر V مانند زیر تعریف کرد:

$$\large E= - \nabla V$$

برای یک محیط خطی و ایزوتروپیک داریم:

$$\large D=\varepsilon E$$

به این ترتیب، معادله اول به معادله زیر تبدیل می‌شود:

$$\large \nabla . \varepsilon E = \rho$$

پس خواهیم داشت:

$$\large \nabla . (\varepsilon \nabla V) = -\rho$$

که در آن، $$\varepsilon$$ می‌تواند از تابعی از مکان باشد. برای یک محیط ساده و همگن، $$\varepsilon$$ یک مقدار ثابت دارد و می‌توان آن را از اپراتور دیورژانس خارج کرد. پس داریم:

$$\large\nabla^2 V = - \frac{\rho}{\varepsilon}$$

در معادله بالا $$\nabla^2$$ اپراتور لاپلاس نام دارد. این اپراتور، معادل دیورژانس گرادیان یا $$\nabla. \nabla$$ است. معادله بالا به نام «معادله پواسون» (Poisson's Equation) نیز شناخته می‌شود. این رابطه بیان می‌کند که برای یک محیط ساده، لاپلاسین پتانسیل با $$-\rho / \varepsilon$$ برابر است. در این معادله، $$\varepsilon$$ ضریب گذردهی الکتریکی محیط و $$\rho$$ چگالی حجمی بارهای آزاد است.

این چگالی می‌تواند تابعی از مختصات فضایی باشد. از آنجا که اپراتورهای دیورژانس و گرادیان شامل مشتق‌های فضایی مرتبه اول هستند، معادله پواسون یک معادله دیفرانسیل جزئی مرتبه دوم محسوب می‌شود. این معادله در هر نقطه از فضا که مشتق‌های مرتبه دوم وجود دارد، جواب خواهد داشت. لاپلاسین پتانسیل در مختصات فضایی به صورت زیر نوشته می‌شود:

$$\large \nabla^2 V = \nabla . \nabla V = \left ( a_x \frac{\partial }{\partial x}+a_y \frac{\partial }{\partial y}+ a_z \frac{\partial }{\partial z}\right ). \left ( a_x \frac{\partial V}{\partial x} + a_y \frac{\partial V}{\partial y}+ a_z \frac{\partial V}{\partial z}\right );$$

بنابراین معادله پواسون به صورت زیر قابل بازنویسی است:

$$\large\frac{\partial^2 V}{\partial x^2}+\frac{\partial^2 V}{\partial y^2}+\frac{\partial^2 V}{\partial z^2}= -\frac{\rho}{\varepsilon} \, \, \, (V/m^2)$$

به همین ترتیب، می‌توان لاپلاسین را برای مختصات استوانه‌ای و کروی نیز نوشت. برای مختصات استوانه‌ای، لاپلاسین پتانسیل به صورت زیر نوشته می‌شود:

$$\large\nabla^2 V = \frac{1}{r}\frac{\partial}{\partial r}\left ( r \frac{\partial V}{\partial r} \right) + \frac{1}{r^2} \frac{\partial^2 V}{\partial \phi ^2 }+ \frac{\partial^2 V}{\partial z^2}$$

$$\large\partial^2 V = \frac{1}{R^2}\frac{\partial}{\partial R} \left( R^2 \frac{\partial V}{\partial R} \right)+\frac{1}{R^2 sin \theta }\frac{\partial}{\partial \theta}\left ( sin \theta \frac{\partial V}{\partial \theta} \right ) + \frac{1}{R^2 sin^2 \theta} \frac{\partial ^2 V}{\partial \phi^2}$$

در حل معادله پواسون سه بعدی، شرایط مرزی باید در نظر گرفته شود. اگر در یک محیط ساده بار آزاد الکتریکی وجود نداشته باشد، $$\rho = 0$$ است و معادله پواسون به صورت زیر نوشته می‌شود:

$$\large\nabla ^2 V = 0$$

به این معادله «معادله لاپلاس» (Laplace Equation) گفته می‌شود. این معادله در الکترومغناطیس نقش مهمی دارد. برای حل مسائل مربوط به هادی‌ها، مثل خازن‌ها از معادله لاپلاس استفاده می‌شود. با محاسبه $$V$$ از معادله آخر می‌توان میدان الکتریکی را طبق معادله زیر پیدا کرد:

$$\large E = - \nabla V$$

به این ترتیب، توزیع بار روی سطح هادی از رابطه زیر محاسبه می‌شود:

$$\large \rho _s = \varepsilon E_n$$

حل مسائل الکتریسیته ساکن

در این بخش با حل دو مثال نشان می‌دهیم که چگونه می‌توان از این دو معادله در حل مسائل الکتریسیته ساکن استفاده کرد.

مثال ۱

خازنی با دو صفحه موازی داریم. فاصله این دو صفحه $$d$$ و پتانسیل این صفحات به ترتیب $$0$$ و $$V_0$$ است. شکل زیر این مسئله را نشان می‌دهد:

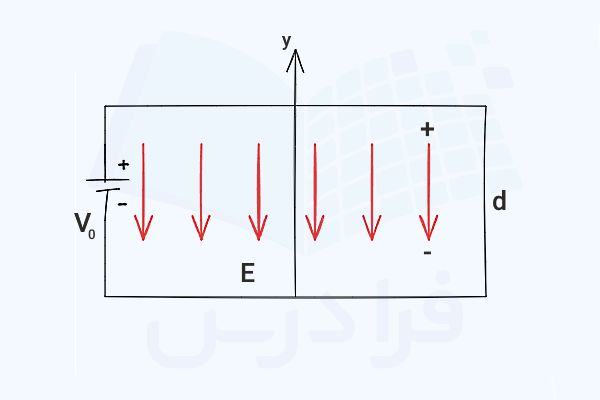
با صرف‌نظر کردن از اثرات میدان در حاشیه لبه‌ها، پتانسیل در هر نقطه بین این دو صفحه و توزیع بار سطحی روی صفحات را بیابید:

پاسخ

برای حل این مسئله و یافتن پتانسیل بین صفحات موازی از معادله لاپلاس استفاده می‌شود. از آنجا که $$\rho = 0$$ است، تابع پتانسیل این مسئله هیچ تغییری در جهات $$x$$ و $$z$$ نخواهد داشت:

$$\large \frac{d^2 V}{d y^2}=0$$

از آنجا که پتانسیل در این مسئله تنها تابع $$y$$ است، می‌توان از $$d^2 / dy^2$$ به جای $$\partial ^2 / \partial^2 y$$ استفاده کرد. با یک بار انتگرال‌گیری از معادله بالا نسبت به $$y$$ خواهیم داشت:

$$\large \frac {dV}{dy} = C_1$$

که در آن ثابت انتگرال‌گیری $$C_1$$ باید تعیین شود. با انتگرال‌گیری مجدد خواهیم داشت:

$$\large V = C_1 y + C_2$$

برای حل این معادله و یافتن ثابت‌های انتگرال‌گیری $$C_1$$ و $$C_2$$، دانستن دو شرط مرزی نیاز است. دو شرط مرزی از پتانسیل روی صفحات به دست می‌آید. به صورت زیر:

$$@\large \, \, \, y= 0 \, \, \, \to \, \, \, V=0$$

$$@ \large \, \, \, y=d \, \, \, \to \, \, \, V=V_0$$

با جایگزین کردن این معادلات در معادله لاپلاس خواهیم داشت:

$$\large V= \frac{V_0}{d} y.$$

پس پتانسیل از $$y=0$$ تا $$y=d$$ به صورت خطی زیاد می‌شود. برای یافتن توزیع بار سطحی ابتدا باید میدان الکتریکی ($$E$$) را در صفحات $$y=0$$ و $$y=d$$ بیابیم. بنابراین داریم:

$$\large E = -\hat a _y \frac{dV}{dy} = -\hat a_y \frac{V_0}{d}$$

میدان الکتریکی به دست آمده، یکنواخت و مستقل از $$y$$ است. ذکر این نکته ضروری است که جهت $$E$$ بر خلاف جهت افزایش $$V$$ است. توزیع بار سطحی در صفحات هادی به صورت زیر محاسبه می‌شود:

$$\large E_n = \hat a_n . E = \frac{\rho_s}{\varepsilon}$$

در صفحه پایینی داریم:

$$\large \hat a_n =\hat a_y \, \, \, , \, \, \, E_{nl} = -\frac{V_0}{d}\, \, \, , \, \, \, \rho_{sl}= - \frac{\varepsilon V_0}{d}$$

همچنین در صفحه بالایی خواهیم داشت:

$$\large \hat a_n = -\hat a_y \, \, \, , \, \, \, E_{nu} = \frac {V_0}{d}\, \, \, , \, \, \, \rho_{su} = -\frac{\varepsilon V_0}{d}$$

خطوط میدان الکتریکی در میدان الکتریکی ساکن، از بارهای مثبت شروع می‌شود و به بار منفی ختم می‌شود.

مثال ۲

میدان الکتریکی را در داخل و خارج یک ابر الکترونی کروی محاسبه کنید، اگر چگالی بار حجمی یکنواخت این ابر کروی برای $$0 \leq R \leq b$$، برابر $$\rho = -\rho _0$$ و برای $$R>b$$، برابر $$\rho =0$$ باشد:

پاسخ

همانطور که می‌دانیم برای محاسبه پتانسیل الکتریکی ابتدا باید معادلات لاپلاس و پواسن یک بعدی حل شوند. از آنجا که تابع پتانسیل هیچ تغییری در جهت‌های $$\theta$$ و $$\phi$$ ندارد، در نتیجه پتانسیل فقط تابعی از شعاع یا $$R$$ در مختصات کروی خواهد بود. برای محاسبه میدان الکتریکی داخل کره داریم:

$$\large 0 \leq R \leq b \, \, \, , \, \, \, \rho = - \rho_0$$

در این ناحیه به دلیل وجود بار الکتریکی آزاد، معادله پواسن برقرار است. با صرفنظر از $$\partial / \partial \theta$$ و $$\partial / \partial \phi$$ خواهیم داشت:

$$\large \frac{1}{R^2}\frac{d}{dR} (R^2 \frac{dV_i}{dR}) = \frac{\rho_0}{\varepsilon _0}$$

این معادله به صورت زیر قابل بازنویسی است:

$$\large \frac{d}{dR} (R^2 \frac{dV_i}{dR})= \frac{\rho_0}{\varepsilon _0}R^2$$

با انتگرال‌گیری از این معادله داریم:

$$\large \frac{dV_i}{dR} = \frac{\rho_0}{3\varepsilon_0}R + \frac{C_1}{R^2}$$

شدت میدان الکتریکی داخل ابر الکترونی برابر است با:

$$\large E_ i = -\nabla V_i = -a_R (\frac{dV_i}{dR})$$

از آنجا که $$E_i$$ در $$R=0$$ نمی‌تواند بی‌نهایت باشد، ثابت انتگرال‌گیری $$C_1$$ از بین می‌رود. به همین ترتیب خواهیم داشت:

$$\large E_i = -a_R \frac{\rho_ 0 }{3 \varepsilon _0 }R, \, \, \, 0 \leq R \leq b$$

حال برای محاسبه میدان الکتریکی بیرون ابر خواهیم داشت:

$$\large R \geq b \, \, \, , \, \, \, \rho = 0$$

در این ناحیه معادله لاپلاس برقرار است، چون بار آزاد وجود ندارد. پس داریم:

$$\large \nabla^2 V_0 = 0 \to \frac{1}{R^2}\frac{\partial }{\partial R}(R^2 \frac{dV_0}{dR})=0$$

با انتگرال‌گیری از این معادله خواهیم داشت:

$$\large \frac{dV_0}{dR}= \frac{C_2}{R^2}$$

یا به صورت معادل:

$$\large E_0 = - \nabla V_0 = -a_R \frac{dV_0}{dR}= -a_R \frac{C_2}{R^2}$$

میدان در داخل و بیرون کره در سطح کره با هم برابر می‌شود. از پیوستگی میدان در سطح کره ($$R=b$$) می‌توان ثابت انتگرال‌گیری $$C_2$$ را محاسبه کرد. پس خواهیم داشت:

$$\large \frac{C_2}{b^2} = \frac{\rho_0}{3 \varepsilon _0}b$$

از این معادله خواهیم داشت:

$$\large C_2 = \frac{\rho_0 b^3}{3 \varepsilon_ 0 }$$

پس میدان بیرون کره عبارت است از:

$$\large E_o = -a_R \frac{\rho_0 b^3}{3 \varepsilon_ 0 R^2} \, \, \, , \, \, \, R \geq b$$

کل بار در ناحیه کروی ابر الکترونی برابر است با:

$$\large Q = - \rho_ 0 \frac{4 \pi}{3}b^3$$

پس می‌توان میدان را به صورت زیر نوشت:

$$\large E_ o = a_R \frac{Q}{4 \pi \varepsilon _0 R^2}$$

که همان میدان الکتریکی برای بار نقطه‌ای $$Q$$ و در فاصله $$R$$ از آن است. اگر دوباره به قبل نگاهی بیندازیم، با یادآوری $$C_1=0$$ خواهیم داشت:

$$\large V_i = \frac{\rho_0 R^2}{6 \varepsilon_ 0}+ C_1^ \prime$$

لازم به ذکر است که $$C_1^\prime$$ یک ثابت انتگرال‌گیری جدید است و با $$C_1$$ برابر نیست. با جایگزینی معادلات و انتگرال‌گیری مجدد خواهیم داشت:

$$\large V_o = - \frac{\rho_0 b^3}{3 \varepsilon_0 R}+ C_2^ \prime$$

$$C_2^\prime$$ باید حذف شود، چرا که $$V_o$$ در بی‌نهایت صفر خواهد شد. پتانسیل الکتریکی در مرز پیوسته است. با برابر قرار دادن $$V_i$$ و $$V_o$$ در $$R=b$$ خواهیم داشت:

$$\large \frac{\rho_ 0 b^2 }{6 \varepsilon _0 }+ C_1^\prime = - \frac{\rho_0 b^2}{3 \varepsilon_0}$$

یا:

$$\large C_1^\prime = -\frac{\rho b^2}{2 \varepsilon _0}$$

بنابراین خواهیم داشت:

$$\large V_i = -\frac{\rho_0}{3 \varepsilon_0} (\frac{3b^2}{2}- \frac{R^2}{2})$$

اگر به مباحث مرتبط در زمینه فیزیک و مهندسی علاقه‌مند هستید، مطالعه مطلب «شرایط مرزی الکترومغناطیسی – از صفر تا صد» از مجله فرادرس به شما پیشنهاد می‌شود.