حد توابع چند متغیره — به زبان ساده

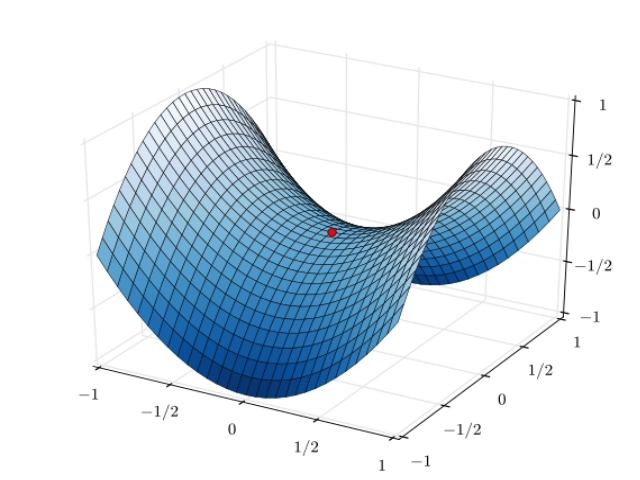
در این مطلب قصد داریم تا مفهوم و روش محاسبه حد توابع چند متغیره را توضیح دهیم. بدین منظور پیشنهاد می‌شود در ابتدا مطالب حد تابع، توابع چند متغیره و پیوستگی توابع مطالعه شوند.

نحوه محاسبه حد توابع چند متغیره

قبل از توضیح نحوه محاسبه حد توابع چند متغیره اجازه دهید تا مفهوم حد در توابع تک متغیره را یادآوری کنیم. حد یک تابع تک متغیره به صورت زیر بیان می‌شود.

$$\large \mathop { \lim } \limits _ { x \to a } f \left ( x \right ) = L$$

فیلم آموزش ریاضی عمومی ۲ + حل مثال در فرادرس

کلیک کنید

در حقیقت حد چپ و راست تابع فوق باید به شکل زیر با هم برابر باشند.

$$\large \mathop { \lim } \limits _ { x \to { a ^ + } } f \left ( x \right ) = \mathop { \lim } \limits _ { x \to { a ^ - } } f \left ( x \right ) = L$$

سمت چپِ عبارت فوق نشان دهنده حد راست تابع است. بنابراین حد راست تابع در یک نقطه به صورت زیر تعریف می‌شود.

$$\large \mathop { \lim } \limits _ { x \to { a ^ + } } f \left ( x \right )$$

به همین صورت، حد چپ تابع نیز برابر است با:

$$\large \mathop { \lim } \limits _ { x \to { a ^ - } } f \left ( x \right )$$

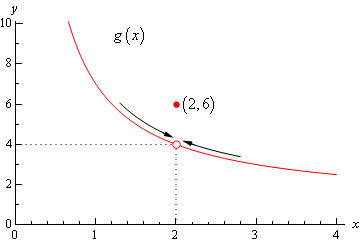
بنابراین زمانی یک تابع در نقطه‌ای مشخص دارای حد است، که حد چپ و راست در آن نقطه با هم برابر باشند. از همین رو در تابع دومتغیره دو مسیر برای نزدیک شدن به x وجود دارد. یک مسیر از مقادیر کمتر از x و دیگری از مقادیر بیشتر از x به a نزدیک می‌شود. در شکل زیر نیز این دو مسیر نشان داده شده است.

حال تابعی دومتغیره را در نظر بگیرید. فرض کنید می‌خواهیم حد تابع را در نقطه (a,b) بدست آوریم. در این صورت مطابق با شکل زیر مسیر‌های زیادی برای رسیدن به نقطه مذکور وجود دارد.

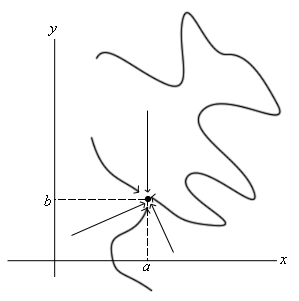
معمولا حد تابع دو متغیره $$f ( x , y )$$ در نقطه (a,b) را به یکی از روش‌های زیر نشان می‌دهند.

$$\large \mathop { \lim } \limits _ { x \to a \atop y \to b } f \left ( { x , y } \right ) \hspace {0.5in} \mathop { \lim } \limits _ { \left ( { x , y } \right ) \to \left ( { a , b } \right ) } f \left ( { x , y } \right )$$

همچون توابع تک متغیره، در این حالت نیز حاصل حدِ ناشی از هریک از مسیر‌ها باید با هم برابر باشند. توجه داشته باشید که برای برقرار بودن حد تابعی دو متغیره در نقطه (a,b) نیازی نیست تا تمامی مسیر‌ها چک شوند.

نکته: تابع دومتغیره $$f \left ( { x , y } \right )$$ زمانی در نقطه (a,b) پیوسته است که رابطه زیر برای آن برقرار باشد.

$$\large \mathop { \lim } \limits _ { \left ( { x , y } \right ) \to \left ( { a , b } \right ) } f \left ( { x , y } \right ) = f \left ( { a , b } \right )$$

توجه داشته باشید تمامی توابع پیوسته‌ای که می‌شناسیم، با قرار دادن هر چند متغیر در آن، پیوسته باقی می‌ماند. در ادامه مثال‌هایی ارائه شده که پیشنهاد می‌شود، آن‌ها را مطالعه فرمایید.

مثال ۱

حاصل حدود زیر را در صورت وجود بدست آورید.

1. $$\large \mathop { \lim } \limits _ { \left ( { x , y , z } \right ) \to \left ( { 2 , 1 , - 1 } \right ) } 3 { x ^ 2 } z + y x \cos \left ( { \pi x - \pi z } \right )$$
2. $$\large \displaystyle \mathop { \lim } \limits _ { \left ( { x , y } \right ) \to \left ( { 5 , 1 } \right ) } \frac { { x y } } { { x + y } }$$

فیلم آموزش حسابان ۲ – پایه دوازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

(۱): این تابع ترکیب دو تابع چند جمله‌ای و تابع مثلثاتی است. بنابراین پیوسته نیز هست. حاصل حد تابع در نقطه خواسته شده نیز برابر است با:

$$\large \mathop { \lim } \limits _ { \left ( { x , y , z } \right ) \to \left ( { 2 , 1 , - 1 } \right ) } 3 { x ^ 2 } z + y x \cos \left ( { \pi x - \pi z } \right )$$

(۲): این تابع روی مسیر y=-x پیوسته نیست. دلیل این ناپیوستگی، صفر شدن مخرج کسر روی مسیر مذکور است. بدیهی است که نقطه (5,1) روی این مسیر قرار ندارد. بنابراین تابع در این نقطه نیز پیوسته خواهد بود. حد تابع نیز در این نقطه برابر است با:

$$\large \mathop { \lim } \limits _ { \left ( { x , y } \right ) \to \left ( { 5 , 1 } \right ) } \frac { { x y } } { { x + y } } = \frac { 5 } { 6 }$$

در دو مثال بالا نکته خاصی در محاسبه حد وجود نداشت و تنها با جایگذاری x و y حاصل حد‌ها را بدست آوردیم. در برخی از موارد باید از رفع ابهام استفاده کرد. در مثال ۲ نمونه‌ای از این رفع ابهام ارائه شده است.

مثال ۲

حاصل حد زیر را بدست آورید.

$$\large \mathop { \lim } \limits _ { \left ( { x , y } \right ) \to \left ( { 1 , 1 } \right ) } \frac { { 2 { x ^ 2 } - x y - { y ^ 2 } } } { { { x ^ 2 } - { y ^ 2 } } }$$

اگر $$( 1 , 1 )$$ را در تابع قرار دهید، خواهید دید حد به صورت $$\frac { 0 } { 0 }$$ است. بنابراین تابع در نقطه مذکور پیوسته نبوده و باید از تکنیک‌های رفع ابهام استفاده کرد. در نتیجه با استفاده از فاکتورگیری داریم:

$$\large \mathop { \lim } \limits _ { \left ( { x , y } \right ) \to \left ( { 1 , 1 } \right ) } \frac { { 2 { x ^ 2 } - x y - { y ^ 2 } } } { { { x ^ 2 } - { y ^ 2 } } } = \mathop { \lim } \limits _ { \left ( { x , y } \right ) \to \left ( { 1 , 1 } \right ) } \frac { { \left ( { 2 x + y } \right ) \left ( { x - y } \right ) } } { { \left ( { x - y } \right ) \left ( { x + y } \right ) } } = \mathop { \lim } \limits _ { \left ( { x , y } \right ) \to \left ( { 1 , 1 } \right ) } \frac { { 2 x + y } } { { x + y } }$$

همان‌طور که می‌بینید در توابع چند متغیره نیز می‌توان با حذف عوامل صفر از صورت و مخرج، حاصل حد را بدست آورد. نهایتا داریم:

$$\large \mathop { \lim } \limits _ { \left ( { x , y } \right ) \to \left ( { 1 , 1 } \right ) } \frac { { 2 { x ^ 2 } - x y - { y ^ 2 }} } { { { x ^ 2 } - { y ^ 2 } } } = \mathop { \lim } \limits _ { \left ( { x , y } \right ) \to \left ( { 1 , 1 } \right ) } \frac { { 2 x + y } } { { x + y } } = \frac { 3 } { 2 }$$

توجه داشته باشید که در مواردی، حتی نمی‌توان از روش‌ فاکتور‌گیری نیز استفاده کرد. در ادامه مثالی ذکر شده که در آن از مفاهیم اساسی حد استفاده شده است.

مثال ۳

حاصل حدود زیر را بدست آورید.

1. $$\large \displaystyle \mathop { \lim } \limits _ { \left ( { x , y } \right ) \to \left( {0,0} \right)} \frac { { { x ^ 2 } { y ^ 2 } } } { { { x ^ 4 } + 3 { y ^ 4 } } }$$
2. $$\large \displaystyle \mathop {\lim }\limits_{\left( {x,y} \right) \to \left( {0,0} \right)} \frac { { { x ^ 3 } y } } { { { x ^ 6 } + { y ^ 2 } } }$$

فیلم آموزش ریاضی عمومی 2 – جامع و کاربردی در فرادرس

کلیک کنید

(۱): با جایگذاری نقطه (۰,0) در تابع، می‌بینید کسر به صورت $$\frac { 0 } { 0 }$$ در می‌آید. بنابراین باید از تکنیک‌های رفع ابهام استفاده کرد. از طرفی ظاهر کسر نشان می‌دهد که نمی‌توان از فاکتورگیری استفاده کرد.

با توجه به ناپیوسته بودن تابع در نقطه مد نظر،‌ اگر پاسخِ حد از دو مسیر متفاوت، مقادیر مختلفی باشد، می‌توان نتیجه گرفت تابع در نقطه (۰,0) حد ندارد. با انتخاب مسیر، تابع، به صورت تک متغیره در آمده و می‌توان به راحتی حاصل حد را محاسبه کرد. نکته بسیار مهم در انتخاب مسیر‌ها این است که نقطه (۰,0) باید روی مسیر‌های مذکور قرار داشته باشد.

در حالت اول روی محور x قرار داریم و به نقطه (۰,0) نزدیک می‌شویم. بنابراین در این حالت مسیر انتخابی، همان محور x یا به عبارتی y=0 است. در این حالت حاصل حد برابر است با:

$$\large \mathop { \lim } \limits _ { \left ( { x , y } \right ) \to \left ( { 0 , 0 } \right ) } \frac { { { x ^ 2 } { y ^ 2 } } } { { { x ^ 4 } + 3 { y ^ 4 } } } = \mathop { \lim } \limits _ { \left ( { x , 0 } \right ) \to \left( {0,0} \right)} \frac { { { x ^ 2 } { { \left ( 0 \right ) } ^ 2 } } } { { { x ^ 4 } + 3 { { \left ( 0 \right) } ^ 4 } } } = \mathop {\lim }\limits_{\left( {x,0} \right) \to \left ( { 0 , 0 } \right ) } 0 = 0$$

بنابراین اگر روی محور x به نقطه (۰,0) نزدیک شویم، حدِ تابع برابر با صفر خواهد بود. در حالت دوم فرض کنید که روی محور y حرکت کرده و به مبدا یا (۰,0) نزدیک می‌شویم. در حقیقت در این حالت مسیر در نظر گرفته شده همان x=0 است. حاصل حد در این حالت برابر است با:

$$\large \mathop { \lim } \limits _ { \left ( { x , y } \right ) \to \left ( { 0 , 0 } \right ) } \frac { { { x ^ 2 } { y ^ 2 } } } { { { x ^ 4 } + 3 { y ^ 4 } } } = \mathop {\lim } \limits _ { \left ( { 0 , y } \right ) \to \left ( { 0 , 0 } \right ) } \frac { { { { \left( 0 \right ) } ^ 2 } { y ^ 2 } } } { { { { \left ( 0 \right ) } ^ 4 } + 3 { y ^ 4 } } } = \mathop {\lim }\limits_{\left( {0,y} \right) \to \left( {0,0} \right)} 0 = 0$$

بنابراین اگر روی محور‌های x یا y حرکت کرده و به مبدا نزدیک شویم، حاصل حد برابر با صفر است. اما آیا تنها با استفاده از این دو مسیر می‌توان نتیجه گرفت حاصل حد در نقطه (۰,0) برابر با صفر است؟ پاسخ منفی است. در حالت سوم فرض کنید مسیر حد تابع y=x در نظر گرفته می‌شود. حاصل حد در این حالت برابر است با:

$$\large \mathop {\lim }\limits_{\left( {x,y} \right) \to \left( {0,0} \right)} \frac{{{x^2}{y^2}}}{ { { x ^ 4 } + 3 { y ^ 4 } } } = \mathop { \lim } \limits _ { \left ( { x , x } \right ) \to \left ( { 0 , 0 } \right ) } \frac { { { x ^ 2 } { x ^ 2 } } } { { { x ^ 4 } + 3 { x ^ 4 } } } = \mathop { \lim } \limits _ { \left ( { x , x } \right ) \to \left ( { 0 , 0 } \right ) } \frac { { { x ^ 4 } } } { { 4 { x ^ 4 } } } = \mathop { \lim }\limits _ { \left( { x , x } \right ) \to \left ( { 0 , 0 } \right ) } \frac { 1 } { 4 } = \frac{1}{4}$$

همان‌طور که می‌بینید حاصل حد روی مسیر y=x برابر با $$\frac{1}{4}$$ است. بنابراین این تابع در نقطه مذکور حد ندارد.

(۲): حاصل این حد نیز در نقطه (0,0) مبهم است. از این رو دو مسیر y=x و y=x³ را برای محاسبه حد انتخاب می‌کنیم.

مسیر y=x:

$$\large \mathop {\lim }\limits_{\left( {x,y} \right) \to \left( {0,0} \right)} \frac{{{x^3}y}}{{{x^6} + {y^2}}} = \mathop {\lim }\limits_{\left( {x,x} \right) \to \left( {0,0} \right)} \frac{{{x^3}x}}{{{x^6} + {x^2}}} = \mathop {\lim }\limits_{\left( {x,x} \right) \to \left( {0,0} \right)} \frac{{{x^4}}}{{{x^6} + {x^2}}} = \mathop {\lim }\limits_{\left( {x,x} \right) \to \left( {0,0} \right)} \frac{{{x^2}}}{{{x^4} + 1}} = 0$$

مسیر y=x³:

$$\large \mathop {\lim }\limits_{\left( {x,y} \right) \to \left( {0,0} \right)} \frac{{{x^3}y}}{{{x^6} + {y^2}}} = \mathop {\lim }\limits_{\left( {x,{x^3}} \right) \to \left( {0,0} \right)} \frac{{{x^3}{x^3}}}{{{x^6} + {{\left( {{x^3}} \right)}^2}}} = \mathop {\lim }\limits_{\left( {x,{x^3}} \right) \to \left( {0,0} \right)} \frac{{{x^6}}}{{2{x^6}}} = \mathop {\lim }\limits_{\left( {x,{x^3}} \right) \to \left( {0,0} \right)} \frac{1}{2} = \frac{1}{2}$$

فیلم آموزش ریاضی پایه دانشگاهی – جامع و کاربردی در فرادرس

کلیک کنید

همان‌طور که می‌بینید حاصل حد در این دو حالت نیز متفاوت هستند. بنابراین این تابع نیز در نقطه مذکور حد ندارد. در سوالات مطرح شده در مورد حد توابع چند متغیره معمولا دو یا سه مسیر را بررسی کنید و در صورت برابر بودن حد،‌ به احتمال زیاد تابع در نقطه مذکور دارای حد است.

در صورت علاقه‌مندی به مباحث مرتبط در زمینه ریاضی، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس ریاضی
• مجموعه آموزش‌های ریاضی و فیزیک
• قضیه گرین -- به زبان ساده
• انتگرال دوگانه — به زبان ساده
• معادله لاپلاس — از صفر تا صد
• توابع چند متغیره - به زبان ساده

^^