فرادرس
ثابت فنر چیست و به چه عواملی بستگی دارد؟ – به زبان ساده
فنرها اجسام مکانیکی کشسانی هستند که پس از تغییر شکل و کشیده یا فشرده شدن، به شکل اصلی خود بازمیگردند. از فنرها به صورت گسترده در بسیاری از وسایل مکانیکی، مانند انواع اسباببازیها، استفاده میشود. دلیل استفاده گسترده از فنر در ساخت وسیلههای مختلف، توانایی آن در ذخیره انرژی مکانیکی است. یکی از مشخصات مهم فنر که نقش مهمی در طراحی و ساخت فنر ایفا میکند، ثابت فنر نام دارد. ثابت فنر رابطه خطی بین نیرو و میزان جابهجایی فنر را نشان میدهد. در این مطلب ثابت فنر را به زبانه ساده توضیح و آزمایشی ساده برای تعیین ثابت هر فنر را با یکدیگر انجام میدهیم.
ثابت فنر چیست ؟
ثابت فنر، پارامتری ریاضی است که در قانون هوک از آن استفاده میشود. این ثابت، میزان سختی فنر در برابر تغییر شکل را نشان میدهد. در ادامه این بخش، قانون هوک را به صورت خلاصه بیان میکنیم و رابطه ریاضی آن را مینویسیم. هنگامیکه بر جسمی نیرو وارد میکنیم، حالتهای زیر ممکن است رخ دهند:
- جسم فشرده میشود.
- جسم کشیده میشود.
- جسم خمیده میشود.
- جسم بدون تغییر شکل حرکت میکند.
شاید از خود بپرسید چه هنگام نیروی وارد شده بر جسم میتواند شکل آن را تغییر دهد. تغییر شکل جسم در اثر اعمال نیرو به ویژگی به نام کشسانی مربوط میشود. شاید از خود بپرسید کشسانی چیست و چگونه تعریف میشود. یکی از اتفاقاتی که برای جسم پس از اعمال نیرو رخ میدهد، تغییر شکل آن است. جسمی را در نظر بگیرید که نیرویی برابر F بر آن وارد و سبب تغییر شکل جسم میشود. فرض کنید نیروی وارد شده بر جسم حذف و جسم به شکل و حالت اولیه خود بازمیگردد. در این حالت میگوییم جسم از خود رفتار کشسانی نشان میدهد. اگر بخواهیم جسمی پس از اعمال نیرو ساکن بماند، باید بیش از یک نیرو بر آن وارد کنیم. در غیر این صورت جسم، همراه با تغییر شکل، حرکت نیز میکند و از مکان اولیه خود به مکان دیگری در راستای اعمال نیرو حرکت میکند.
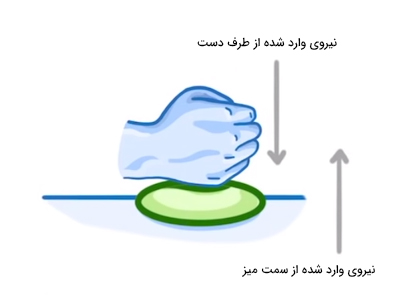
فرض کنید اسفنجی روی میز قرار دارد و شما دست خود را مشت میکنید و اسنفج را فشار میدهید. اسفنج حرکت نمیکند، تنها فشرده میشود. شاید از خود بپرسید چرا اسفنج با اعمال یک نیرو، حرکت نمیکند. به این نکته توجه داشته باشید که میز نیز نیرویی عمودی و به سمت بالا بر اسفنج وارد میکند. بنابراین، بر اسفنج دو نیرو وارد میشود:
- نیروی وارد شده از طرف دست شما که جهت آن عمود بر میز و به سمت پایین است.
- نیروی وارد شده از سمت میز بر اسفنج که جهت آن به سمت بالا است.
این دو نیرو با یکدیگر برابر هستند، بنابراین اسفنج، تنها فشرده میشود و از جای خود حرکت نمیکند.
اجسام پس از اعمال نیرو بر آنها به دو صورت تغییر شکل میدهند:
- تغییر شکل کشسان: تغییر شکل کشسان را در تعریف کردیم. اگر جسم پس از حذف نیرو به شکل اولیه خود بازگردد، تغییر شکل آن کشسان خواهد بود.
- تغییر شکل غیرکشسان: اگر جسم پس از حذف نیرو نتواند به طور کامل به شکل اولیه خود برگردد، تغییر کل آن غیرکشسان است.
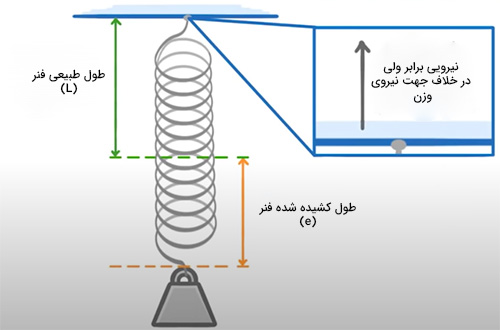
کشش مفهوم دیگری است که باید تعریف کنیم. به افزایش طول فنر پس از کشیدن آن، کشش گفته میشود. فرض کنید فنری را به صورت عمودی آویزان و انتهای آن را به نقطهای ثابت کردهایم. با اعمال نیروی رو به پایین به فنر میتوانیم تغییر طول آن را اندازه بگیریم. این نیرو به انتهای آزاد فنر وارد میشود. اگر فنر نشان داده شده در تصویر زیر را جرمدار در نظر بگیریم، نیروی وزن برابر $$Mg$$ به سمت پایین بر آن وارد میشود. بنابراین، طول طبیعی فنر کمی کوتاهتر خواهد بود. زیرا فنر به دلیل نیروی وزن خود کمی کشیده میشود.
افزایش طول فنر به دلیل نیروی وزن آن بسیار کوچک است. بنابراین، میتوانیم از Hن در مقابل طول کلی فنر چشمپوشی کنیم. سپس، جسمی با جرم مشخص را به انتهای آزاد فنر اضافه میکنیم. نیروی وزنِ جسمِ اضافه شده به فنر به سمت پایین بر فنر وارد میشود. از اینرو، طول فنر افزایش مییابد. افزایش طول فنر را میتوانیم به عنوان طول کشیده شده فنر اندازه بگیریم. آیا تنها نیروی وارد شده بر فنر، وزن جسم اضافه شده به آن است؟ خیر. انتهای ثابت فنر نیز نیرویی برابر ولی در جهت مخالف بر فنر وارد میکند. به همین دلیل، با اضافه کردن جرم به انتهای آزاد، فنر سقوط نخواهد کرد.
با افزایش نیروی وارد شده به انتهای آزاد فنر (افزایش جرم متصل به فنر)، افزایش طول آن بیشتر میشود. بنابراین، اینگونه به نظر میرسد که نیروی وارد شده به فنر رابطه مستقیم با افزایش طول فنر دارد:
$$F \propto e$$
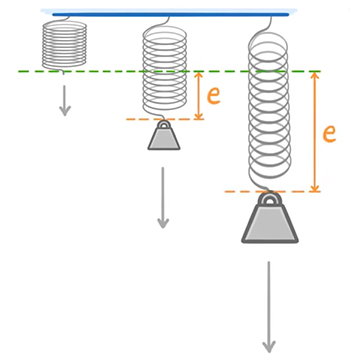
سوال مهمی که ممکن است مطرح شود آن است که با اعمال نیرویی با اندازه مشخص، طول فنر چه اندازه افزایش مییابد. افزایش طول فنر پس از اعمال نیرو بر آن، به کمیتی به نام ثابت فنر بستگی دارد. ثابت فنر با حرف انگلیسی k نشان داده میشود. k را به معادله $$F \propto e$$ اضافه میکنیم. بنابراین، علامت تناسب به شکل تساوی درمیآید و معادله به شکل زیر نوشته میشود:
$$F = k e \enspace F = kx$$
ثابت فنر به ما میگوید برای افزایش طول فنر به اندازه یک متر، چند نیوتن نیرو باید به آن وارد کنیم. بنابراین، هرچه ثابت فنر بزرگتر باشد، جسم سختتر خواهد بود. زیرا برای کشیدن فنر به نیروی بزرگتری نیاز داریم. رابطه $$ F = kx$$ را میتوانیم با رسم نمودار نیرو برحسب میزان کشش فنر به صورت تصویری نشان دهیم. همانطور که در تصویر زیر دیده میشود، با افزایش نیرو، میزان کشش فنر نیز افزایش مییابد. نمودار نیرو بر حسب کشش فنر، نموداری خط است که از مبدأ مختصات میگذرد. این بدان معنا است که در غیاب نیرو، کشش فنر برابر صفر خواهد بود. نیروی وارد شده بر فنر با میزان کشش فنر، رابطه خطی دارد. به این رابطه خطی، قانون هوک میگوییم. در مورد این قانون در بخشهای بعد به صورت مفصلتر صحبت خواهیم کرد.
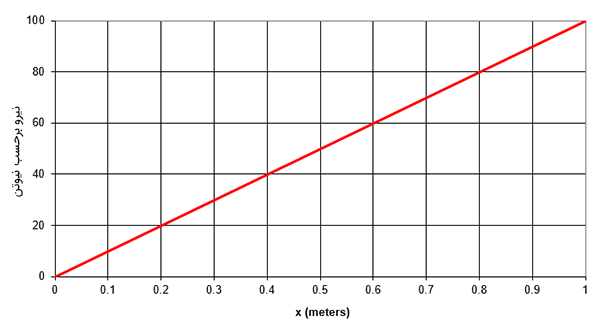
به این نکته توجه داشته باشید که تغییر طول فنر از نوع تغییر طول کشسانی است، زیرا پس از حذف نیرو، فنر به شکل اولیه خود بازمیگردد. همچنین، قانون هوک تا نقطه مشخصی برقرار است. به بیان دیر، تا افزایش نیروی مشخصی، طول فنر به صورت خطی با افزایش نیرو افزایش مییابد. به این نقطه، حد کشسانی میگوییم. پس از گذر از این نقطه، کشش فنر دیگر به صورت خطی با نیرو تغییر نمیکند و نمودار از حالت خطی به صورت نشان داده شده در تصویر زیر درمیآید. پس از این نقطه، قانون هوک برقرار نخواهد بود.
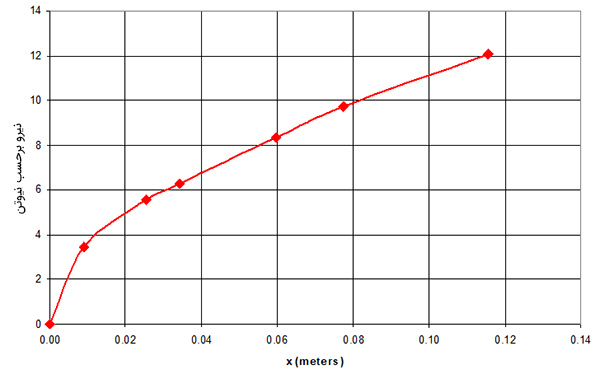
تا اینجا با تعریف ثابت فنر و به اختصار با ثابت فنر آشنا شدیم. در ادامه، در مورد فنر و قانون هوک با جزییات بیشتری صحبت میکنیم.
قانون هوک چیست ؟
قبل از صحبت در مورد قانون هوک، کمی در مورد فنرها صحبت میکنیم. فنری را فرض کنید که روی میز قرار دارد و یکی از سرهای آزاد آن به دیوار متصل شده است. در این حالت، هیچ نیرویی بر فنر وارد نمیشود، بنابراین فنر در حالت طبیعی خود قرار دارد.
در ادامه، نیرویی برابر ۵ نیوتن بر فنر وارد و آن را فشرده میکنیم. فرض کنید فنر به اندازه ۱۰ متر فشرده میشود. فنرها با اعمال نیرو، فشرده یا کشیده میشوند. سوالی که ممکن است مطرح شود آن است که میزان فشردگی یا کشیدگی فنر برحسب نیروهای مختلف چگونه تغییر میکند. به عنوان مثال، اگر به جای ۵ نیوتن، نیرویی برابر ۱۰ نیوتن بر فنر وارد کنیم، فنر چه مقدار فشرده میشود؟ بر طبق درک شهودی خواهید گفت که میزان فشردگی فنر بیشتر از ۱۰ متر است، اما سوال اصلی آن است که چه مقدار؟ آیا جابهجایی فنر پس از اعمال نیرو به صورت خطی با مقدار نیروی اعمال شده تغییر میکند یا رابطه بین جابهجایی فنر و اندازه نیروی وارد شده غیرخطی است؟
در ادامه، نیرویی برابر ۱۰ نیوتن بر فنر وارد میکنیم. فنر چه مقدار جابجا میشود؟ بر طبق آزمایشهای انجام شده، فنر به اندازه ۲۰ متر جابجا خواهد شد. به بیان دیگر، میزان جابهجایی فنر به صورت خطی با مقدار نیروی وارد شده بر آن تغییر میکند. به طور مثال، اگر نیروی وارد شده بر فنر a برابر شود، مقدار جابهجایی آن نیز a برابر خواهد شد. به این نکته توجه داشته باشید که خطی بودن رابطه بین نیروی وارد شده بر فنر و جابهجایی آن به جهت نیروی وارد شده وابسته نیست.
به طور حتم در آزمایشگاههای فیزیک دبیرستان با فنرها کار کردهاید. فنرها پس از اعمال نیرو بر آنها تمایل دارند به حالت طبیعی (طول طبیعی) خود بازگردند. به نیرویی که سبب بازگشت فنر به طول طبیعی خود میشود، نیروی بازگرداننده گفته میشود. این نیرو از نظر بزرگی برابر نیروی وارد شده بر فنر، اما در خلاف جهت آن است و سعی میکند فنر را به حالت طبیعی خود بازگرداند. نیروی بازگرداننده فنر و جابهجایی آن با استفاده از رابطه زیر به یکدیگر مربوط میشوند:
$$F = - k x$$
بار دیگر تصویر فنر فشرده شده را در نظر بگیرید. مبدأ مختصات را حالت طبیعی فنر در نظر میگیریم و جهت راست را به عنوان جهت مثبت انتخاب میکنیم. نیروی ۵ نیوتنی وارد شده بر فنر در خلاف جهت مثبت انتخاب شده است، بنابراین، علامت آن منفی خواهد بود. فنر پس از اعمال این نیرو به اندازه ۱۰ متر فشرده میشود. از آنجا که فنر فشرده شده و انتهای آن قبل از مبدأ مختصات قرار گرفته است، جابهجایی آن را نیز منفی در نظر میگیریم.
$$F = - \ kx \\ F = - \ k \times ( - 10 \ m )= 10 k$$
به این نکته توجه داشته باشید که k را مثبت در نظر میگیریم. بنابراین، نیروی بازگرداننده مثبت است. همانطور که در مطالب بالا اشاره کردیم، نیرو بازگرداننده سعی دارد فنر را به حالت طبیعی خود بازگرداند. در نتیجه،جهت آن در خلاف جهت نیروی وارد شده به فنر خواهد بود. همچنین، نیروی بازگرداننده و نیروی وارد شده بر فنر با یکدیگر برابر هستند. از اینرو، نیروی بازگرداننده برابر ۵ نیوتن خواهد بود.
$$5 = 10 k \\ k = \frac { 5 } { 10 } = \frac { 1 } { 2 } $$
با بهدست آوردن ثابت k میتوانیم جابهجایی فنر پس از اعمال نیروی ۱۰ نیوتنی به آن را بهدست اوردیم. حدس اولیه قبل از محاسبه مقدار جابهجایی برابر ۲۰ مترو در جهت منفی است. برای پاسخ به این پرسش ابتدا باید بدانیم مقدار نیروی بازگرداننده چیست. در مطالب بالا فهمیدیم نیروی بازگرداننده برابر نیروی وارد شده به فنر است. چرا؟ پس از اعمال نیروی F، فنر به اندازه d جابجا میشود و به نقطه b میرسد. در نقطه b فنر در حالت سکون قرار دارد و حرکت نمیکند. از آنجا که برایند نیروهای وارد شده بر جسم ساکن یا جسمی که با سرعت ثابت حرکت میکند، برابر صفر است، علاوه بر نیروی F، نیروی دیگری نیز باید برابر این نیرو و در خلاف جهت آن بر فنر وارد شود. به این نیرو، نیروی بازگرداننده میگوییم و تمایل دارد فنر را به حالت طبیعی خود برگرداند
اندازه نیروی بازگرداننده = اندازه نیروی وارد شده بر فنر
در بخش قبل گفتیم k ثابت فنر نام دارد. در این مثال، مقدار آن را برابر $$\frac { 1 } { 2 }$$ بهدست آوردیم. در نتیجه، میزان جابهجایی فنر پس از اعمال نیروی ۱۰ نیوتنی بر آن برابر است با:
$$10 = - \frac { 1 } { 2 } \times x \\ x = - \ 2 \times 10 = - \ 20 \ m$$
بنابراین، حدس اولیه ما صحیح بود. به رابطه $$F = - k x$$ قانون هوک گفته میشود. هوک، فیزیکدانی انگلیسی در قرن هفدهم میلادی بود که پس از انجام آزمایشهای مختلف به رابطه $$F = - k x$$ رسید.
واحد ثابت فنر چیست ؟
ثابت فنر کمیتی ریاضی است که در قانون هوک ظاهر میشود و واحد آن نیوتن بر متر است. قانون هوک را به صورت زیر مینویسیم:
$$F = - k x$$
در رابطه فوق، F نیروی لازم برای کشیدن یا فشردن فنر، $$x$$ جابهجایی فنر پس از اعمال نیرو و k ثابت فنر است. ثابت فنر به ما میگوید فشردن یا کشیدن فنر سخت است یا آسان. به بیان دیگر، هر چه k بزرگتر باشد، کشیدن یا فشرده شدن فنر به نیروی بزرگتری نیاز دارد. بنابراین، ثابت فنر اطلاعاتی در مورد سختی فنر و مقدار نیروی لازم برای فشردن یا کشیدن آن به ما میدهد. از اینرو، نام دیگر ثابت فنر، سختی فنر است. برای بهدست آوردن واحد ثابت فنر، ابتدا رابطه $$F = - k x$$ را برحسب k مرتب میکنیم:
$$k = - \frac { F } { x }$$
واحد نیرو در سیستم SI برابر نیوتن (N) و واحد جابهجایی برابر متر است. در نتیجه، واحد k برابر $$\frac { N } { m }$$ خواهد بود. واحد k برحسب کمیتهای اصلی در فیزیک چیست؟ برای بهدست آوردن واحد ثابت فنر برحسب کمیت اصلی باید نیوتن را برحسب این واحدها بنویسیم:
$$F = m a \\ N= kg \times \frac { m } { s ^ 2 } = \frac { kg \enspace m } { s ^ 2 }$$
در نتیجه، واحد ثابت فنر بر حسب کمیتهای اصلی برابر است با:
$$k = \frac { N } { m } = \frac { kg \enspace m } { s ^ 2 } \times \frac { 1 } { m } = \frac { kg } { s ^ 2 }$$
تا اینجا فهمیدیم ثابت فنر و واحد اندازهگیری آن چیست. همچنین، با قانون هوک آشنا شدیم. در ادامه، در مورد عوامل موثر بر ثابت فنر و چگونگی بهدست آوردن آن صحبت میکنیم.
ثابت فنر به چه عواملی بستگی دارد ؟
ثابت فنر به عواملی مانند قطر سیم، قطر سیمپیچ، طول آزاد فنر، تعداد سیمپیچهای فعال و ماده سازنده فنر بستگی دارد. همانطور که در مطالب بالا اشاره شد ثابت فنر، اندازهگیری میزان سختی فنر در برابر کشیده یا فشرده شدن است. هرچه میزان سختی فنر بیشتر باشد، مقاومت آن در برابر تغییر طول نیز بیشتر خواهد بود. شاید از خود بپرسید ثابت فنر به چه عواملی بستگی دارد. عاملهای موثر بر ثابت فنر عبارت هستند از:
- قطر سیم: به طور معمول، فنر از سیمهای فلزی ساخته میشوند. قطر سیم سازنده فنر یکی از عاملهای موثر بر اندازه ثابت فنر است.
- قطر سیمپیچ
- طول آزاد: طول فنر در حالت سکون بر سختی فنر تاثیر میگذارد.
- تعداد سیمپیچهای فعال: تعداد سیمپیچهایی که فشرده یا کشیده میشوند.
- ماده سازنده فنر: جنس مادهای که فنر از آن ساخته میشود بر سختی فنر یا ثابت فنر تاثیر میگذارد.
ثابت فنر به صورت مستقیم متناسب با قطر سیمپیچ است. به بیان دیگر، با افزایش قطر سیمپیچ، ثابت فنر نیز افزایش خواهد یافت. در مقابل، ثابت فنر به صورت معکوس با تعداد سیمپیچهای فعال، طول آزاد و قطر فنر تغییر میکند.
سوال مهمی که ممکن است برایتان مطرح شود آن است که چگونه میتوانیم ثابت فنر را بهدست آوریم. آزمایشهای مختلفی برای محاسبه ثابت فنر وجود دارند که در بخش بعد چند آزمایش مهم را با یکدیگر بررسی میکنیم.
چگونه ثابت فنر را به دست می آوریم ؟
در این بخش ثابت فنر فنری دلخواه را با استفاده از آزمایشی ساده بهدست میآوریم. وسایل موردنیاز برای انجام این آزمایش عبارت هستند از:
- فنر
- پایه فلزی
- وزنههای مختلف
- خط کش چوبی عمودی برای اندازهگیری
- نشانگر
- قلاب
فنری را به شکل نشان داده شده در تصویر زیر و به صورت عمودی از پایهای فلزی آویزان میکنیم. در این حالت، طول فنر در حالت عادی قرار دارد. به انتهای آزاد فنر نشانگری متصل میکنیم. با استفاده از این نشانگر میتوانیم تغییر طول فنر را اندازه بگیریم. همانطور که در تصویر زیر مشاهده میکنید، خطکش چوبی عمودی را به گونهای قرار میدهیم که نشانگر متصل به فنر عدد مشخصی را روی خطکش نشان دهد.
در این آزمایش، برای اندازهگیری ثابت فنر از دو روش پویا (دینامیک) و ایستا (استاتیک) استفاده میکنیم.
روش ایستا
فنری را در نظر بگیرید که به صورت عمودی آویزان شده است. قبل از اعمال نیرو بر فنر، طول آن برابر $$x$$ است. نیرویی برابر F و رو به پایین بر فنر وارد میکنیم. طول فنر پس از اعمال نیرو برابر $$x + \triangle x$$ میشود. بنابراین، تغییر طول فنر برابر است با:
$$( x + \triangle x ) - ( x) = \triangle x$$
نیروی F با $$\triangle x$$ به صورت مستقیم متناسب است:
$$F \propto \triangle x$$
با قرار دادن ثابت فنر، k، در کنار $$\triangle x$$ تساوی برقرار میشود:
$$F = k \triangle x$$
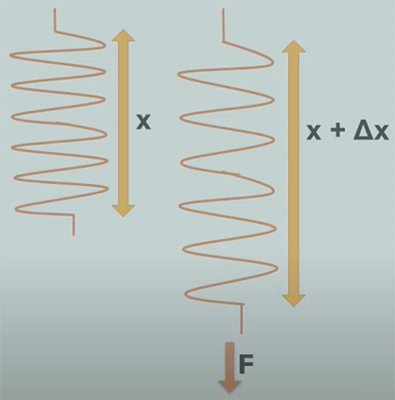
در ادامه، جرمهای مختلف را به انتهای آزاد فنر متصل میکنیم. برای انجام این کار از قلاب کمک میگیریم. ابتدا قلاب را به تنهایی به انتهای فنر متصل میکنیم. همانطور که در تصویر زیر دیده میشود پس از اتصال قلاب به انتهای فنر، فنر کمی کشیده میشود و طول آن افزایش مییابد.
سپس، یکی از وزنهها با جرم مشخص را روی کفه قلاب قرار میدهیم. فنر باز هم کشیدهتر میشود و طول آن افزایش مییابد. هرچه جرم وزنههای اضافه شده به انتهای فنر بیشتر باشد، تغییر طول آن نیز بیشتر خواهد بود. به بیان دیگر، با افزایش جرم وزنهها، نیروی وارد شده به انتهای فنر افزایش مییابد. نیرو با تغییر طول فنر رابطه مستقیم دارد. در نتیجه، تغییر طول فنر نیز بزرگتر خواهد بود. برای انجام این آزمایش، ۶ وزنه با جرمهای ۱۰۰، ۱۵۰، ۲۰۰، ۲۵۰، ۳۰۰ و ۳۵۰ گرم را انتخاب میکنیم و به ترتیب هر یک از آنها را روی کفه قلاب قرار میدهیم و مکان نشانگر را از روی خطکش میخوانیم.
ابتدا قلاب را به انتهای فنر متصل میکنیم و مکان نشانگر روی خطکش چوبی را میخوانیم. عدد نشانگر را با $$x_1$$ نشان میدهیم. سپس، جرمهای ۱۰۰ تا ۳۵۰ گرم را روی کفه قلاب قرار میدهیم و مکان نشانگر را برای هر وزنه میخوانیم و آن را $$x_2$$ مینامیم. سپس جدول زیر را کامل میکنیم. فرض کنید مقدار $$x_1$$ برابر ۰/۶ سانتیمتر بهدست میآید.
| شماره وزنهها | جرم وزنهها برحسب گرم | مقدار $$x_2$$ برحسب سانتیمتر و متر | مقدار $$x_1$$ برحسب سانتیمتر و متر | میزان کشیدگی فنر برحسب متر
$$\triangle x = x_ 2 -x _ 1$$ |
| ۱ | ۱۰۰ | ۲/۷ سانتیمتر یا ۰/۰۲۷ متر | ۰/۶ سانتیمتر یا ۰/۰۰۶ متر | ۲/۷ متر |
| ۲ | ۱۵۰ | ۴/۲ سانتیمتر یا ۰/۰۴۲ متر | ۰/۶ سانتیمتر یا ۰/۰۰۶ متر | ۴/۲ متر |
| ۳ | ۲۰۰ | ۵/۶ سانتیمتر یا ۰/۰۵۶ متر | ۰/۶ سانتیمتر یا ۰/۰۰۶ متر | ۵/۶ متر |
| ۴ | ۶/۹ | ۶/۹ سانتیمتر یا ۰/۰۶۹ متر | ۰/۶ سانتیمتر یا ۰/۰۰۶ متر | ۶/۹ متر |
| ۵ | ۳۰۰ | ۸/۰ سانتیمتر یا ۰/۰۸۰ متر | ۰/۶ سانتیمتر یا ۰/۰۰۶ متر | ۸/۰ متر |
| ۶ | ۳۵۰ | ۹/۷ سانتیمتر یا ۰/۰۹۷ متر | ۰/۶ سانتیمتر یا ۰/۰۰۶ متر | ۹/۷ متر |
به احتمال زیاد از خود پرسیدهاید چرا طول به متر تبدیل شده است. دلیل این موضوع به واحد اندازهگیری ثابت فنر برمیگردد. در رابطه هوک، نیرو باید برحسب نیوتن و جابهجایی باید برحسب متر نوشته شوند. همچنین، از تغییر طول فنر پس از اتصال قلاب به آن چشمپوشی کردهایم. در ادامه، میزان کشیدگی فنر، $$\triangle x$$، پس از اتصال هر وزنه را برحسب جرم متصل به فنر رسم میکنیم. برای رسم این نمودار از نرمافزار اکسل استفاده میکنیم.
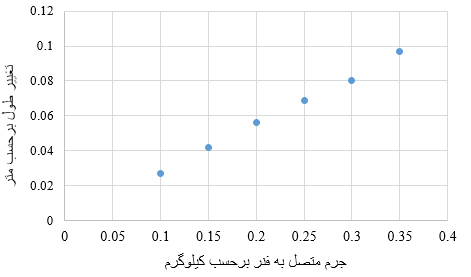
همانطور که در تصویر بالا دیده میشود، نمودار تغییر طول فنر برحسب جرم متصل به آن، خطی مستقیم با شیب ثابت است. شیب این خط بسیار مهم است و برای بهدست آوردن ثابت فنر باید مقدار آن را بدانیم. چرا؟ نیروی وارد شده به فنر به صورت مستقیم متناسب با تغییر طول آن است:
$$F= k \triangle x$$
در این آزمایش مقدار نیروی F برابر نیروی وزنِ جرمِ متصل به فنر و جهت آن رو به پایین است.
$$F = mg$$
رابطه $$F= k \triangle x$$ را در رابطه $$F = mg$$ جایگزین میکنیم:
$$mg = k \triangle x$$
رابطه بهدست آمده را برحسب k مرتب میکنیم:
$$k = \frac { m g } { \triangle x } \\ k = \frac { m } { \triangle x } \times g$$
$$\frac { m } { \triangle x }$$ برابر عکس شیب نمودار رسم شده در بالا است. بنابراین، برای محاسبه k باید شیب نمودار رسم شده در بالا را بهدست آوریم. سپس آن را برعکس میکنیم و در رابطه $$ k = \frac { m } { \triangle x } \times g$$ قرار دهیم. برای بهدست آوردن شیب نمودار میتوانیم از برازش حداقل مربعات استفاده کنیم. این کار را به راحتی میتوانیم با استفاده از نرمافزار اکسل انجام دهیم.
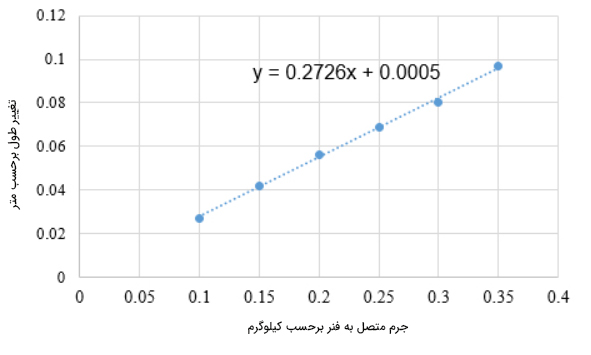
با توجه به نمودار بالا، شیب نمودار برابر ۰/۲۷۲۶ است. بنابراین، ثابت فنر برابر است با:
$$k = 0.2726 \times 9.8 = 2.67 \ \frac { N } { m }$$
روش پویا
روش دوم برای محاسبه ثابت فنر، روش پویا یا دینامیک نام دارد. قبل از انجام این آزمایش باید با نوسانگر هارمونیک ساده آشنا شویم.
نوسانگر هارمونیک ساده
ذرهای را در نظر بگیرید که به فنری با ثابت فنر k متصل شده است. نیروی بازگرداننده به صورت متناوب بر ذره وارد میشود و سعی دارد آن را به حالت تعادل بازگرداند. این نیرو متناسب با جابهجایی ذره از حالت تعادل است و به صورت زیر نوشته میشود:
$$F = - \ kx$$
نیروی بازگرداننده F از قانون هوک میآید. بر طبق این قانون، نیروی بازگرداننده متناسب با جابهجایی ذره از حالت تعادل است.
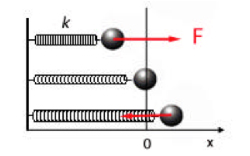
مقدار $$x$$ در رابطه $$F = - \ kx$$ در حالت تعادل برابر صفر، در حالت کشیدگی فنر، مثبت و در حالت فشردگی آن، منفی خواهد بود. همچنین، علامت منفی در رابطه $$F = - \ kx$$ به دلیل آن است که نیروی بازگرداننده F همواره در خلاف جهت جابهجایی است. بر طبق قانون دوم نیوتن، نیرو با شتاب حرکت جسم رابطه مستقیم دارد و به صورت زیر نوشته میشود:
$$F = m a $$
از ترکیب دو رابطه $$F = - \ kx$$ و $$F = m a $$ داریم:
$$-k x = ma$$
شتاب برابر مشتق دوم جابهجایی نسبت به زمان است و به صورت زیر نوشته میشود:
$$a = \frac{\text{d}^ 2 x}{\text{d}t ^ 2}$$
با قرار دادن شتاب در رابطه $$-k x = ma$$، داریم:
$$ - k x = m \ \frac{\text{d}^ 2 x}{\text{d}t ^ 2}$$
عبارتها را در یک طرف تساوی مینویسیم و برابر صفر قرار میدهیم:
$$m \ \frac{\text{d}^ 2 x}{\text{d}t ^ 2} + k x = 0$$
طرفین رابطه فوق را بر m تقسیم میکنیم:
$$ \ \frac{\text{d}^ 2 x}{\text{d}t ^ 2} +\frac { k } { m } x = 0$$
با تعریف کسر $$\frac { k } { m }$$ به صورت $$\omega ^ 2$$ داریم:
$$\frac{\text{d}^ 2 x}{\text{d} t ^ 2} + \omega ^ 2 x = 0$$
برای حل این معادله دیفرانسیل، عبارتی را به عنوان حل معادله حدس میزنیم:
$$x ( t ) = A \sin \omega t + B \cos \omega t$$
اگر پاسخ کلی فوق را در معادله $$\frac{\text{d}^ 2 x}{\text{d} t ^ 2} + \omega ^ 2 x = 0$$ قرار دهیم، به تساوی $$0 = 0$$ میرسیم. بنابراین، ذره متصل به فنر به صورت تناوبی حرکت میکند و حرکت آن به زمان وابسته است. به این حرکت، حرکت هارمونیک ساده میگوییم و به سیستم متناظر آن، نوسانگر هارمونیک گفته میشود. نوسان با فرکانس زاویهای ثابت رخ میدهد که مقدار آن برابر است با:
$$\omega = \sqrt { \frac { k } { m } }$$
به این فرکانس، فرکانس طبیعی نوسانگر میگوییم. فرکانس زاویهای یا دایرهای برحسب هرتز نیز به صورت زیر نوشته میشود:
$$\nu = \frac { \omega } { 2 \pi } = \frac { 1 } { 2 \pi } \sqrt { \frac { k } { m }} \ Hz$$
در روش پویا، سیستم را به صورت نوسانگر هارمونیک در نظر میگیریم. همانطور که در بخش قبل گفتیم به فنر، جرمهای مختلف متصل میکنیم. بنابراین، $$m$$ در رابطه فرکانس، جرم متصل به فنر است. به این نکته توجه داشته باشید که اگر فنر جرم داشته باشد به $$m$$ جرم فنر نیز افزوده خواهد شد. فرکانس و دوره تناوب عکس یکدیگر هستند، بنابراین دوره تناوب نوسانگر هارمونیک به صورت زیر نوشته میشود:
$$T = 2 \pi \sqrt { \frac { m } { k } }$$
طرفین رابطه فوق را به توان دو میرسانیم و آن را برحسب ثابت فنر مرتب میکنیم:
$$k = \frac { 4 \pi ^ 2 } { T ^ 2 } \ m $$
برای انجام آزمایش، جرم متصل به فنر را به آهستگی به سمت پایین میکشیم و آن را رها میکنیم. چه اتفاقی رخ میدهد؟ فنر و جرم متصل به آن با آهنگ ثابتی شروع به نوسان میکند. با استفاده از زمانسنج یا کرنومتر زمان ۲۵ نوسان کامل را اندازه میگیریم. شاید از خود بپرسید چگونه یک نوسان کامل را بشماریم. به یک رفت و برگشت کامل جرم متصل به فنر، یک نوسان گفته میشود. در شروع حرکت، جرم متصل به فنر را تا به سمت پایین میکشیم. پس از رسیدن نشانگر به عددی مشخص روی خطکش، جرم را رها میکنیم. جرم به دلیل نیروی بازگرداننده وارد شده بر آن به سمت نقطه تعادل حرکت میکند. در نقطه تعادل، انرژی جنبشی جرم بیشینه و انرژی پتانسیل آن برابر صفر است.
بنابراین، جسم به حرکت خود ادامه میدهد و به صورت متقارن، اما در جهت مخالف، به سمت بالا حرکت میکند. در فاصلهای مشخص از نقطه تعادل، انرژی جنبشی برابر صفر، اما انرژی پتانسیل بیشنه میشود. همچنین، در این نقطه نیروی بازگرداننده در جهت مخالف جابهجایی تمایل به بازگرداندن جسم به نقطه تعادل دارد. جسم برای بار دوم به نقطه تعادل میرسد. در این نقطه، بار دیگر انرژی جنبشی آن بیشینه و انرژی پتانسیل آن برابر صفر است. بنابراین، جرم متصل به فنر به حرکت خود ادامه میدهد و پس از عبور از نقطه تعادل به نقطه اولیه رها شده میرسد و این حرکت باز هم تکرار میشود. به هر رفت و برگشت جسم یک نوسان میگوییم. مدت زمان ۲۵ نوسان را برای جرم ۱۰۰ گرمی متصل به فنر بهدست میآوریم.
در ادامه، جرمی برابر ۱۵۰ گرم را به انتهای فنر متصل و بار دیگر مدت زمان ۲۵ نوسان را اندازه میگیریم و به ترتیب این کار را برای جرمهای بیشتر تا ۳۵۰ گرم انجام میدهیم و جدول زیر را کامل میکنیم.
| شماره وزنهها | جرم وزنهها برحسب گرم | مقدار $$T$$ برحسب ثانیه |
| ۱ | ۱۰۰ | |
| ۲ | ۱۵۰ | |
| ۳ | ۲۰۰ | |
| ۴ | ۶/۹ | |
| ۵ | ۳۰۰ | |
| ۶ | ۳۵۰ |
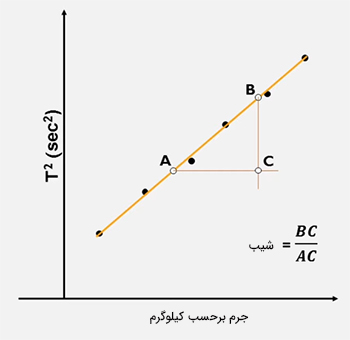
پس از اندازهگیری دوره تناوب برای هر جرم، آنها را به توان دو میرسانیم و نمودار مربع دوره تناوب برحسب جرم متصل به فنر را رسم میکنیم. برای بهدست آوردن نتیجه دقیقتر بهتر است نمودار را در نرمافزار اکسل رسم کنیم و شیب را بهدست آوریم. برای یافتن رابطه بین شیب و ثابت فنر، تنها کافی است $$T^2$$ را برحسب جرم متصل به فنر بنویسیم.
$$k = \frac { 4 \pi ^ 2 } { T ^ 2 } \ m \\ T ^ 2 = \frac { 4 \pi^ 2 } { k } \ m$$
نمودار $$T^2$$ را برحسب m نموداری خطی و شیب آن برابر $$\frac { 4 \pi^ 2 } { k } $$ است. از اینرو، با داشتن شیب نمودار به راحتی میتوانیم ثابت فنر را بهدست آوریم.
در این بخش فهمیدیم چگونه با انجام دو آزمایش ساده در خانه یا در آزمایشگاه فیزیک در مدرسه میتوانیم ثابت فنری دلخواه را بهدست آوریم. توجه به این نکته مهم است که گاهی ممکن است با بیش از یک فنر سروکار داشته باشیم. فنرها ممکن است همانند مقاومت یا خازن در مدارهای الکتریکی به صورت سری، موازی یا ترکیبی از این دو حالت بسته شوند. بنابراین، آشنایی با چگونگی محاسبه ثابت فنر کلی مجموعهای از فنرها ضروری است. اما قبل از پرداختن به این مبحث، با یکدیگر چند مثال ساده در مورد فنرهای تکی و ثابت آنها حل میکنیم.
نمونه سوالات ثابت فنر
فنرها پس از کشیده شدن یا رها شدن تمایل دارند به حالت طبیعی خود برگردند. ثابت فنر به ما میگوید مقدار نیروی لازم برای بازگشت فنر به حالت طبیعی چه مقدار است. ثابت فنر با استفاده از رابطه زیر بهدست میآید:
$$k = \frac { F } { x }$$
از رابطه فوق میتوانیم برای بهدست آوردن ثابت فنری ایدهال استفاده کنیم. همچنین، قانون هوک به صورت ریاضی و با استفاده از رابطه $$F = - \ k x $$ بیان میشود. در قانون هوک باید به نکتههای زیر توجه کنیم:
- علامت منفی نشان میدهد که نیروی ثابت فنر در خلاف جهت نیروی وارد شده بر فنر قرار دارد. علامت منفی به معنای منفی بود مقدار عددی کمیت موردنظر نیست.
- استفاده از قانون هوک محدودیتهای زیادی دارد. از این قانون، تنها میتوانیم برای مواد کشسان یا الاستیک و در محدود حد کشسانی آنها استفاده کنیم. اگر جسمی بیشتر از حد معمول کشیده شود و نتواند به حالت طبیعی خود بازگردد، آن جسم از محدوده کشسانی خود خارج شده است. در این حالت نمیتوانیم از قانون هوک استفاده کنیم.
- قانون هوک بر پایه قانون سوم نیوتن، قانون عمل و عکسالعمل، است. بر طبق این قانون، برای هر عملی، عکسالعملی برابر و در خلاف جهت آن وجود دارد.
در مطالب بالا فهمیدیم چندین عامل از جمله طول فنر بر مقدار ثابت فنر تاثیر میگذارند. ثابت فنر به صورت معکوس با طول تعادلی فنر تغییر میکند. این بدان معنا است که هرچه طول فنر بلندتر باشد، نیروی لازم برای بازگشت فنر به حالت تعادل یا طول طبیعی آن کمتر خواهد بود. در مقابل، هرچه فنر کوتاهتر باشد، نیروی لازم برای بازگشت آن به حالت تعادل نیز بیشتر است. ثابت فنر، سختی فنر را اندازه میگیرد. فنرهای کوتاهتر سختتر از فنرهای بلندتر هستند. به عنوان مثال، اگر فنری را از وسط نصف کنید، ثابت فنر آن دو برابر خواهد شد. در مقابل، اگر طول فنری را دو برابر کنید، ثابت فنر آن نصف میشود. همچنین، اگر نیروی یکسانی را بر دو فنر با طولهای متفاوت وارد کنید، فنر بلندتر در مقایسه با فنر کوتاهتر بیشتر کشیده میشود.
مثال اول ثابت فنر
جسمی به وزن ۰/۱ نیوتن به فنری متصل و فنر به اندازه $$x$$ از طول طبیعی خود کشیده شده است. اگر جسم دیگری با وزنِ مشابه ۰/۱ نیوتن را به فنر وصل کنیم، فنر به اندازه ۳/۵ سانتیمتر دیگر کشیده میشود. ثابت فنر چه مقدار است؟
پاسخ
ابتدا فنر در حالت عادی و تعادل قرار دارد. جسمی به وزن ۰/۱ نیوتن به آن متصل و فنر به اندازه $$x$$ کشیده میشود. $$x$$ را نمیدانیم، اما ندانستن مقدار آن تاثیری بر محاسبه سختی فنر ندارد و ثابت فنر همواره ثابت است. در ادامه، جسم دیگری به وزن ۰/۱ نیوتن به انتهای فنر وصل میکنیم و فنر به اندازه ۳/۵ سانتیمتر دیگر کشیده میشود. برای بهدست آوردن ثابت فنر از رابطه زیر استفاده میکنیم:
$$k = \frac { F } { x }$$
از آنجا که واحد اندازهگیری فنر برابر $$\frac { N } { m }$$ است، مقدار کشیدگی فنر را باید از سانتیمتر به متر تبدیل کنیم. ۳/۵ سانتیمتر برابر ۰/۰۳۵ متر است. در ادامه، مقدار نیرو و تغییر طول فنر را در رابطه $$k = \frac { F } { x }$$ قرار میدهیم.
$$k = \frac { 0.1 } { 0.035 } = 2.85 \ \frac { N } { m }$$
شاید از خود پرسیده باشید چرا به جای ۰/۰۳۵ متر مقدار $$0.035+x$$ و به جای نیرو، مقدار ۰/۲ نیوتن را قرار ندادیم. زیرا مقدار کشیدگی فنر پس از اتصال جسم اول به آن را نمیدانیم، تنها کشیدگی فنر پس از اتصال جسم دوم به آن را میدانیم.
مثال دوم ثابت فنر
مقدار نیروی لازم برای کشیدن فنری به اندازه ۱/۵ متر را بهدست آورید. ثابت فنر برابر $$0.7 \ \frac { N } { m }$$ است.
پاسخ
برای حل این مثال از معادله قانون هوک بدون علامت منفی استفاده میکنیم:
$$F = kx$$
در این مثال مقدار کشیدگی فنر برحسب متر داده شده است، با قرار دادن مقدارهای داده شده در رابطه فوق، مقدار F را بهدست میآوریم:
$$F = kx \\ F = 0.7 \times 1.5 = 1.05 \ N$$
مثال سوم ثابت فنر
فردی به وزن ۶۷۰ نیوتن روی ترازو میایستد و فنر ترازو به اندازه ۰/۷۹ سانتیمتر فشرده میشود. ثابت فنر ترازو را بهدست آورید.
پاسخ
برخلاف دو مثال اول که در آنها فنر کشیده شده است، در این مثال فنر فشرده میشود. وزن فرد برابر ۶۷۰ نیوتن است. او روی ترازو میایستد تا جرم خود را اندازه بگیرد. نیروی وارد شده بر فنرِ ترازو چه مقدار است؟ ۶۷۰ نیوتن. وزن شخص ایستاده روی ترازو برابر نیروی وارد شده بر فنر است. از آنجا که واحد اندازهگیری فنر برابر $$\frac { N } { m }$$ است، مقدار کشیدگی فنر را باید از سانتیمتر به متر تبدیل کنیم. ۰/۷۹ سانتیمتر برابر ۰/۰۰۷۹ متر است. در نتیجه، ثابت فنر برابر است با:
$$k = \frac { F } { x } \\k = \frac { 670 } { 0.0079 } = 84810 \ \frac { N } { m }$$
ثابت فنر بسیار بزرگ است. این بدان معنا است که فنر در برابر نیروهای وارد شده به آن مقاومت میکند و تغییر طول آن بسیار کوچک است.
مثال چهارم ثابت فنر
به فنری با ثابت فنر k نیرویی برابر ۲۵ نیوتن وارد میشود و فنر به اندازه ۲۸۰ سانتیمتر کشیده میشود. مقدار k را بهدست آورید.
پاسخ
از آنجا که یکای اندازهگیری فنر برابر $$\frac { N } { m }$$ است، مقدار کشیدگی فنر را باید از سانتیمتر به متر تبدیل کنیم. ۲۸۰ سانتیمتر برابر ۲/۸۰ متر است. در نتیجه، ثابت فنر برابر است با:
$$k = \frac { F } { x } \\k = \frac { 25 } { 2.80 } = 8.93 \ \frac { N } { m }$$
مثال پنجم ثابت فنر
ثابت فنری برابر ۸۷۵ نیوتن بر متر است. مقدار جرم لازم برای اتصال به انتهای فنر برای کشیدگی آن به اندازه ۴/۵ سانتیمتر چه مقدار است؟
پاسخ
در این مثال باید نیروی وارد شده بر فنر برای تغییر طول آن به اندازه ۴/۵ سانتیمتر را بهدست آوریم. ابتدا تغییر طول فنر را از سانتیمتر به متر تبدیل میکنیم. ۴/۵ سانتیمتر برابر ۰/۰۰۴۵ متر است. در نتیجه، نیروی وارد شده بر فنر برابر است با:
$$F = k x \\ F = 870 \times 0.0045 = 3.9 \ N$$
از آنجا که باید مقدار جرم متصل به فنر را بهدست آوریم، مقدار نیروی بهدست آمده را بر شتاب جاذبه زمین تقسیم میکنیم:
$$m = \frac { W } { g } \\ m = \frac { 3.9 } { 10 } = 0.39 \ kg$$
مثال ششم ثابت فنر
دو فنر با ثابتهای فنر متفاوت داریم. چگونه میتوان فنر با ثابت فنر بزرگتر را بهدست آورد؟
پاسخ
در این پرسش، دو فنر با ثابتهای فنر متفاوت داریم. برای آنکه بدانیم ثابت فنر کدام فنر بزرگتر است میتوانیم از قانون هوک استفاده کنیم. بر طبق این قانون، ثابت فنر با مقدار کشیدگی یا فشردگی فنر به صورت معکوس تغییر میکند. بنابراین، فنری که کمتر کشیده یا فشرده شود، ثابت فنر آن بیشتر است. بر طبق قانون هوک، نیروی اعمال شده برای بازگردان فنر به طول طبیعی خود متناسب با میزان کشیدگی یا فشردگی فنر است:
$$F = - \ k x$$
دو فنر با ثابتهای فنر متفاوت داریم. برای آنکه بدانیم کدام فنر ثابت فنر بزرگتری دارد، آزمایشی ساده طراحی میکنیم. دو فنر را به صورت نشان داده شده در تصویر زیر از سقف آویزان و دو جسم با جرمهای یکسان به انتهای هر کدام متصل میکنیم. هر کدام از فنرها به مقدار مشخصی کشیده میشوند، اما میزان کشیدگی آنها متفاوت است. فنری که کمتر کشیده میشود، ثابت فنر کوچکتری دارد. دلیل این موضوع آن است که ثابت فنر و میزان کشیدگی فنر معکوس یکدیگر هستند. در نتیجه، فنری که کمتر کشیده شود، ثابت فنر کوچکتری خواهد داشت.
مثال هفتم ثابت فنر
مقدار نیروی لازم برای آنکه بتوانیم فنری با ثابت فنر ۲۰ نیوتن بر متر را به اندازه ۲۵ سانتیمتر بکشیم چه مقدار است؟
پاسخ
ثابت فنر برابر ۲۰ نیوتن بر متر و مقدار کشیدگی آن برابر ۲۵ سانتیمتر است. از آنجا که یکای اندازهگیری ثابت فنر $$\frac { N } { m }$$ است، باید مقدار کشیدگی را از سانتیمتر به متر تبدیل کنیم. از اینرو، مقدار کشیدگی فنر برابر ۰/۲۵ متر است. همانطور که در تصویر زیر مشاهده میکنید فنر به صورت افقی قرار گرفته است و آن را با نیروی مشخصی میکشیم.
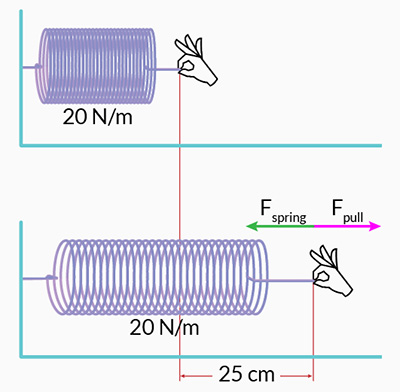
پس از آنکه فنر به اندازه ۲۵ سانتیمتر کشیده میشود، نیروی $$F_ { spring }$$ بر فنر در جهت منفی (چپ) وارد میشود و سعی در بازگرداندن فنر به حالت تعادل (طول عادی) دارد. نیروی F با استفاده از رابطه زیر بهدست میآید:
$$F = k \triangle x \\ F = 20 \ \frac { N } { m } \times 0.25 \ m \\ F = 5 \ N$$
بنابراین، مقدار نیروی لازم برای کشیدن فنر به اندازه ۲۵ سانتیمتر برابر ۵ نیوتن است.
مثال هشتم ثابت فنر
فنری به صورت نشان داده شده در تصویر زیر به صورت عمودی روی زمین قرار دارد و انتهای آن به نقطهای روی زمین ثابت شده است. جسمی به جرم ۴ کیلوگرم روی فنر قرار داده میشود و فنر به اندازه ۲ سانتیمتر فشرده میشود.
- ثابت فنر چه مقدار است؟
- مقدار انرژی ذخیره شده در فنر چه مقدار است؟
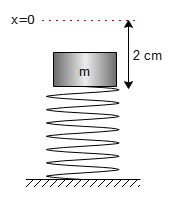
پاسخ
در این مثال، فنر به صورت عمودی قرار گرفته و در نقطهای به زمین ثابت شده است. در تمام مثالهای مربوط به قانون هوک هنگامیکه جسمی به جرم m روی فنری با ثابت k قرار میگیرد، ثابت فنر، k، با استفاده از رابطه زیر بهدست میآید:
$$kx = mg \\ k = \frac { m g } { x } $$
قسمت ۱: ثابت فنر را با استفاده از رابطه بالا بهدست میآوریم:
$$k = \frac { mg } { x } \\ = \frac { 4 \times 10 } { 0.0 2} \\ k = 2000 \ \frac { N } { m }$$
قسمت ۲: انرژی پتانسیل فنر با استفاده از رابطه زیر بهدست میآید:
$$PE_s = \frac { 1 } { 2 } k x ^ 2 \\ PE_s = \frac { 1 } { 2 } ( 2000 ) ( 0.02 ) ^ 2 = 0.4 \ J$$
مثال نهم ثابت فنر
جسمی با جرم نامشخص به فنر عمودی با ثابت فنر ۳۵۰ نیوتن بر متر متصل شده است. اگر فنر به اندازه ۷ سانتیمتر کشیده شود، جرم جسم برابر است با:
۲/۴۵ کیلوگرم
۳/۰۰ کیلوگرم
۲/۰۰ کیلوگرم
۱/۴۵ کیلوگرم
فنر به سقف متصل شده است. دو نیرو بر جسم وارد میشوند:
- نیروی گرانش یا نیروی وزن و به سمت پایین بر جسم وارد میشود.
$$F_ g = mg$$
- نیروی فنر که به سمت بالا بر جسم وارد میشود.
$$F_ s = k x $$
از آنجا که جسم آویزان شده از فنر در حالت تعادل قرار دارد، نیروهای وارد شده بر آن باید با یکدیگر برابر باشند:
$$F _ s = F_ g \\ kx = mg \\ m = \frac { k x } { g } \\ = \frac { 350 \times 0.07 } { 10 } \\ m = 2.45 \ kg$$
توجه به این نکته مهم است که علامت منفی در فرمول اصلی قانون هوک، $$F_s = - \ kx $$، به ما نشان میدهد که جهت نیروی وارد شده بر فنر و مقدار جابجایی آن، همواره در خلاف جهت یکدیگر قرار دارند. در این مثال، جسم آویزان شده از فنر با استفاده از وزن خود، آن را به سمت پایین میکشاند. بنابراین، فنر به سمت پایین جابجا میشود. در نتیجه، نیروی وارد شده از سمت فنر بر جسم باید به سمت بالا باشد.
مثال دهم ثابت فنر
سبدی پر از سیب و به جرم ۶ کیلوگرم به ترازوی فنری با ثابت فنر ۴۵۰ نیوتن بر متر آویزان شده است. میزان کشیدگی فنر چه مقدار است؟
۰/۱۵ متر
۰/۱۴ متر
۰.۱۳ متر
۰/۱۵ متر
این مثال را میخواهیم با روش متفاوتی حل کنیم. در اینجا بیشتر در مورد علامت منفی در قانون هوک و نقش آن در حل مسائل مشابه صحبت خواهیم کرد. همانطور که در مطالب بالا اشاره شد علامت منفی در رابطه $$F _ s = - \ k x$$ نشان میدهد که نیروی وارد شده توسط فنر در خلاف جهت جابجایی آن از حالت تعادل است. اگر بخواهیم مثالهای قانون هوک را با روش برداری حل کنیم، علامت منفی باید در نظر گرفته شود. در حل برداری ابتدا باید جهتی را به عنوان جهت مثبت انتخاب کنیم. $$y = 0$$ را مبدأ فرضی در نظر میگیریم و جهت بالا را به عنوان جهت مثبت انتخاب میکنیم.
سبد سیب، ساکن و بدون حرکت است، بنابراین برایند نیروهای وارد شده بر آن باید برابر صفر باشد. از اینرو نیروی وزن به سمت پایین با نیروی فنر به سمت بالا باید با یکدیگر برابر باشند. فنر پس از آویزان شدن سبد سیب به آن کشیده میشود. بنابراین، جابجایی آن در خلاف جهتِ مثبتِ انتخاب شده و منفی است. بر طبق علامت منفی نوشته شده در قانون هوک، نیروی فنر باید به سمت بالا و مقدار آن برابر $$kx $$ باشد. بر طبق قانون دوم نیوتن، برایند نیروهای وارد شده بر جسم برابر حاصلضرب جرم جسم در شتاب حرکت آن است:
$$\overrightarrow{F}_ { net} = m \overrightarrow{ a }$$
از آنجا که سبد سیب ساکن است، شتاب حرکت آن برابر صفر است. در نتیجه:
$$\overrightarrow { F } _ {net } = 0 \\ \overrightarrow { F } _ s+ \overrightarrow { F } _ g = 0 \\ kx + ( - m g ) = 0 \\ x = \frac { m g } { k } $$
مقدارهای داده شده را در رابطه بالا قرار میدهیم و مقدار $$x$$ را بهدست میآوریم:
$$x = \frac { 6 \times 9.8 } { 450 } = 0.13 \ m$$
بنابراین، فنر ترازو به اندازه ۱۳ سانتیمتر فشرده میشود.
مثال یازدهم ثابت فنر
نمودار نیروی F برحسب تغییر طول فنر در شکل زیر نشان دادهشده است. ثابت فنر برابر است با: 
۵۰۰ نیوتن بر متر
۴۰۰ نیوتن بر متر
۶۰۰ نیوتن بر متر
۳۰۰ نیوتن بر متر
یکی از راههای بهدست آوردن ثابت فنر رسم نیروی وارد شده بر فنر برحسب جابجایی فنر از حالت تعادل است. این نمودار، خطی مستقیم است که شیب آن، ثابت فنر را به ما میدهد. بنابراین، برای بهدست آوردن ثابت فنر در این مثال، تنها کافی است شیب نمودار خطی را بهدست آوریم. برای بهدست آوردن شیب هر خط مستقیم به دو نقطه روی آن خط نیاز داریم:
$$k = \frac { \triangle F } {\triangle x } \\ k = \frac { F_ 2 - F_1 } { x_ 2 - x_ 1 } = \frac { 20 - 10 } { 0.04 - 0.02 } \\ k = \frac { 10 } { 0.02 } = 500 \ \frac { N } { m }$$
مثال دوازدهم ثابت فنر
طول طبیعی فنر A با ثابت ۱۰۰ نیوتن بر متر برابر ۶۰ سانتیمتر و طول طبیعی فنر B با ثابت ۲۰۰ نیوتن بر متر برابر ۹۰ سانتیمتر است. اگر نیروهای یکسانی بر هر یک از فنرها وارد شوند، تغییر طول فنر A بر تغییر طول فنر B برابر است با:
دو به یک است.
یک به دو است.
سه به یک است.
یک به سه است.
دادههای مسئله عبارت هستند از:
- طول طبیعی فنر A برابر ۶۰ سانتیمتر است.
- ثابت فنر A برابر ۱۰۰ نیوتن بر متر است.
- طول طبیعی فنر B برابر ۹۰ سانتیمتر است.
- ثابت فنر B برابر ۲۰۰ نیوتن بر متر است.
نسبت تغییر طول فنر A به تغییر طول فنر B را میخواهیم بهدست آوریم. تغییر طول فنری دلخواه با استفاده از رابطه زیر بهدست میآید:
$$\triangle l = \frac { F } { k }$$
تغییر طول فنر A برابر است با:
$$\triangle l _ A = \frac { F_ A } { k_A }$$
تغییر طول فنر B برابر است با:
$$\triangle l _ B = \frac { F_ B } { k_B }$$
نیروهای وارد شده بر دو فنر با یکدیگر برابر هستند، بنابراین:
$$F_A = F_ B$$
در نتیجه، نسبت تغییر طول فنر A به تغییر طول فنر B برابر است با:
$$\frac { \triangle l _ A } { \triangle l _ B } = \frac { \frac { F } { k _ A } } { \frac { F } { k _ B }}\\ \frac { \triangle l _ A } { \triangle l _ B } = \frac { \frac { 1 } { 100 } } { \frac { 1 } { 200}} \\ = \frac { \triangle l _ A } { \triangle l _ B } = 2$$
مثال سیزدهم ثابت فنر
نیرویی برابر ۲۰۰ نیوتن بر فنری وارد و آن را به اندازه ۴ متر میکشاند. ثابت فنر چه مقدار است؟
۱۰۰ نیوتن بر متر
۵۰ نیوتن بر متر
۲۵ نیوتن بر متر
۱۵۰ نیوتن بر متر
فرض کنید فنری داریم که به صورت افقی روی زمین قرار گرفته و به نقطهای روی دیوار ثابت شده است. بنابراین، یک انتهای فنر ثابت و انتهای دیگر آن آزاد است. نیرویی برابر $$F_p$$ به سمت راست به انتهای آزادِ فنر وارد میکنیم. نیروی وارد شده به فنر و جابجایی آن مثبت هستند (جهت راست را به صورت قراردادی به عنوان جهت مثبت انتخاب میکنیم). فنر پس از اعمال نیروی $$F_p$$ به آن به اندازه $$x $$ کشیده میشود. $$F_p$$ و $$x$$ با یکدیگر متناسب هستند. بنابراین:
$$F_ p = k x$$
k در رابطه بالا ثابت تناسب یا ثابت فنر نام دارد. همانطور که در مطالب بخشهای قبل گفتیم این معادله تا حد مشخصی به نام حد کشسانی برقرار است. قبل از حد کشسانی، فنر پس از فشرده یا کشیدن شدن تا مقداری مشخص، به طول طبیعی خود بازمیگردد. اما پس از حد کشسانی فن نمیتواند به طول طبیعی خود برگردد. به این نکته توجه داشته باشید که پس از کشیده یا فشرده شدن فنر به اندازه $$x$$، فنر ساکن و در حالت تعادل قرار دارد. بنابراین، نیرویی برابر $$F_p$$ و در خلاف جهت آن باید بر فنر وارد شود. نیروی دوم میخواهد فنر را به حالت طبیعی خود برگرداند. به این نیرو، نیروی بازگرداننده میگوییم و با $$F_s$$ نشان داده میشود. $$F_s$$ منفی $$F_p$$ است و با استفاده از رابطه زیر بهدست میآید:
$$F_S = - \ k x$$
به رابطه فوق، قانون هوک میگوییم. پس از مرور مختصری بر قانون هوک، مثال ۱۳ را با یکدیگر حل میکنیم. نیرویی برابر ۲۰۰ نیوتن بر فنری وارد و آن را به اندازه ۴ متر جابجا میکند.
$$F_p = k x \\ 200 = k \times 4 \\ k = 50 \ \frac { N } { m } $$
مثال چهاردهم ثابت فنر
برای کشیدن فنری به اندازه ۲۵ سانتیمتر به نیرویی برابر ۲۵۰ نیوتن نیاز داریم. اگر نیرویی برابر ۹۰۰ نیوتن بر همان فنر وارد کنیم، چه مقدار کشیده میشود؟
۸۴ سانتیمتر
۹۰ سانتیمتر
۹۲ سانتیمتر
۸۶ سانتیمتر
بر طبق صورت مسئله، اگر نیرویی برابر ۲۵۰ نیوتن بر فنر وارد شود، به اندازه ۲۴ سانتیمتر کشیده خواهد شد. برای آنکه بدانیم نیروی ۹۰۰ نیوتنی چه مقدار فنر را میکشد، باید ثابت فنر را بهدست آوریم. ثابت فنر به صورت زیر بهدست میآید:
$$F = k x \\ k = \frac { F } { x } \\ k = \frac { 250 } { 0.24 } = 1041 \ \frac { N } { m }$$
شاید از خود بپرسید چرا ۲۴ سانتیمتر را به متر تبدیل کردیم. زیرا واحد اندازهگیری ثابت فنر برابر نیوتن بر متر است. بنابراین، باید سانتیمتر را به متر تبدیل کنیم. از آنجا که ثابت فنر همواره مقدار ثابتی است، برای بهدست آوردن مقدار کشیدگی فنر پس از اعمال نیروی ۹۰۰ نیوتنی بر آن، از مقدار بهدست آمده در بالا استفاده میکنیم.
$$F = k x \\ x = \frac { F } { k } = \frac { 900 } { 1041 } = 0.86 \ m$$
مثال پانزدهم ثابت فنر
نیرویی برابر ۴۵۰ نیوتن بر فنری وارد میشود و آن را به اندازه ۲۵ سانتیمتر میکشد. نیروی پتانسیل کشسانی ذخیره شده در فنر چه مقدار است؟
۵۶/۲۵ ژول
۶۶/۲۵ ژول
۶۰ ژول
۷۵ ژول
کار لازم برای کشیدن فنر برابر $$W = \frac { 1 } { 2 } k \triangle x ^ 2$$ است. کار انجام شده توسط نیروی وارد شده بر فنر برابر تغییرات انرژی پتانسیل است.
$$W = \triangle P _ E$$
رابطه فوق هنگامی برقرار است که شتاب حرکت برابر صفر باشد. در این حالت، نیروی وارد شده بر فنر و نیروی بازگرداننده با یکدیگر برابر هستند. کار را میتوانیم به صورت زیر نیز بنویسیم:
$$W = PE_F - PE_I$$
در برخی کتابهای درسی، انرژی پتانسیل کشسانی با $$U_s$$ نشان داده میشود. به جای W در رابطه بالا، رابطه $$W = \frac { 1 } { 2 } k \triangle x ^ 2$$ را قرار میدهیم:
$$ \frac { 1 } { 2 } k \triangle x ^ 2 = PE_ F - PE_I \\ \frac { 1 } { 2 } k ( x_F ^ 2 - x _ o ^ 2 ) = PE_F - PE_I \\ \frac { 1 } { 2 } k x_F ^ 2 - \frac { 1 } { 2 } k x _ o ^ 2 = PE_F - PE_ I $$
رابطه فوق به چه معنا است؟ بر طبق رابطه بهدست آمده در بالا انرژی پتانسیل کشسانی اولیه و نهایی به ترتیب برابر $$\frac { 1 } { 2 } k x_o ^ 2 $$ و $$\frac { 1 } { 2 } k x_F ^ 2 $$ هستند. بنابراین، انرژی پتانسیل کشسانی فنر در حالت کلی با استفاده از رابطه زیر بهدست میآید:
$$PE = \frac { 1 } { 2 } k x ^ 2$$
آیا میدانید تفاوت معادله $$PE = \frac { 1 } { 2 } k x ^ 2$$ با $$W = \frac { 1 } { 2 } k \triangle x ^ 2$$ چیست؟ در رابطه $$W = \frac { 1 } { 2 } k \triangle x ^ 2$$، کار انجام شده به تغییر موقعیت فنر وابسته است. اما در رابطه $$PE = \frac { 1 } { 2 } k x ^ 2$$، انرژی پتانسیل تنها به میزان کشیدگی فنر یا تغییر موقعیت آن نسبت به حالت طبیعی بستگی دارد. در این مثال میخواهیم انرژی ذخیره شده در فنری را بهدست آوریم که به اندازه ۲۵ سانتیمتر کشیده شده است.
$$PE = \frac { 1 } { 2 } k x ^ 2 $$
برای بهدست آوردن مقدار انرژی پتانسیل کشسانی ذخیره شده در فنر باید جابجایی و ثابت فنر را بدانیم. مقدار جابجایی داده شده است، اما چیزی در مورد ثابت فنر نمیدانیم. از اینرو، ابتدا ثابت فنر را بهدست میآوریم:
$$k = \frac { F } { x } \\ k = \frac { 450 } { 0.25 } = 1800 \ \frac { N } { m }$$
در ادامه، ثابت فنر و جابجایی فنر از حالت تعادل را در رابطه انرژی پتانسیل کشسانی قرار میدهیم و مقدار آن را بهدست میآوریم:
$$PE= \frac { 1 } { 2 } \times 1800 \times ( 0.25)^ 2 = 56.25 \ J$$
مثال شانزدهم ثابت فنر
مقدار کار لازم برای کشیدن فنر از نقطه ۴/۵ سانتیمتر به ۸/۲ سانتیمتر چه مقدار است. ثابت فنر برابر ۱۵۰ نیوتن بر متر است.
۰/۲۵۰ ژول
۰/۳۵۲ ژول
۰/۳۰۰ ژول
هیچکدام
فنری را در حالت افقی روی میز در نظر بگیرید که در حالت طبیعی خود قرار دارد. ابتدا نیرویی مشخص به فنر وارد و فنر به اندازه ۴/۵ سانتیمتر کشیده میشود و در مکان A قرار میگیرد. سپس فنر بیشتر کشیده میشود و طول آن تا ۸/۲ سانتیمتر افزایش مییابد. در این حالت فنر در نقطه B قرار دارد. مقدار کار لازم برای کشیدن فنر از نقطه A به نقطه B را میخواهیم. کار انجام شده برای کشیدن فنر از نقطخ A به B با استفاده از رابطه زیر بهدست میآید:
$$W = \frac { 1 } { 2 } k \triangle x ^ 2 \\ W = \frac { 1 } { 2 } k (x _ B ^ 2 - x _ A ^ 2 )$$
مقدارهای داده شده در مثال را در رابطه بالا میگذاریم:
$$W = \frac { 1 } { 2 } \times 150 \times ( (0.082)^ 2 - ( 0.045) ^ 2 ) \\W = 0.352 \ J$$
ثابت فنر در فنرهای سری و موازی
در مطالب بالا در مورد ثابت فنر تکی و قانون هوک صحبت کردیم. اما در حالت کلی ممکن است بیش از یک فنر داشته باشیم. سوالی که ممکن است مطرح شود آن است که ثابت فنر مجموعهای از فنرهای را چگونه بهدست میآوریم. ابتدا فنرهای سری و سپس فنرهای موازی را بررسی میکنیم.
ثابت فنر در فنرهای سری
فنرها ممکن است به صورت سری در کنار یکدیگر قرار گرفته باشند. سری وصل شدن فنرها بدان معنا است که به صورت متوالی و به دنبال یکدیگر قرار گرفتهاند. برای راحتی کار دو فنر با ثابتهای فنر $$k_1$$ و $$k_2$$ را در نظر میگیریم که به صورت سری به یکدیگر وصل شدهاند. این دو فنر را میتوانیم معادل یک فنر با ثابت فنر موثر K در نظر بگیریم. دو فنر سری به صورت نشان داده شده در تصویر زیر به صورت افقی روی میز قرار گرفتهاند و نیروی F بر آنها وارد میشود.
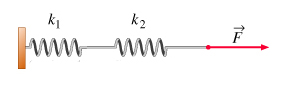
نیروی F بر هر دو فنر وارد میشود. شاید از خود بپرسید مقدار نیروی وارد شده بر فنر اول چه مقدار است. نیروی F بر فنر دوم وارد میشود. آیا نیروی کمتری بر فنر اول وارد میشود؟ خیر. مقدار نیروی وارد شده بر فنر اول نیز برابر F است. بنابراین، بر هر دو فنر نیروی یکسان F وارد میشود. فنر اول و دوم پس از وارد شدنِ نیروی F تا مقداری مشخص کشیده میشوند. فرض کنید میزان کشیدگی دو فنر با یکدیگر برابر $$X$$ باشد. مقدار $$X$$ برابر مجموع کشیدگی فنر اول و دوم است:
$$X = x _1 + x_2 $$
قانون هوک بدون علامت منفی به صورت زیر نوشته میشود:
$$F = k x $$
رابطه فوق را برحسب $$x$$ مرتب میکنیم:
$$x = \frac { F } { k } $$
به جای هر یک از $$x$$ها در رابطه $$X = x _1 + x_2 $$ رابطه $$\frac { F } { k }$$ را قرار میدهیم:
$$\frac { F } { K } = \frac { F } { k _ 1 } + \frac { F } { k _ 2 } $$
با حذف F از طرفین رابطه بالا داریم:
$$\frac { 1 } { K } = \frac { 1 } { k _ 1 } + \frac { 1 } { k _ 2 } $$
$$K$$ ثابت فنر موثر دو فنر سری است. اگر بیشتر از دو فنر به صورت سری به یکدیگر متصل شده باشند، ثابت فنر موثر آنها به صورت زیر بهدست میآید:
$$\frac { 1 } { K } = \frac { 1 } { k _ 1 } + \frac { 1 } { k _ 2 } + \frac { 1 } { k _ 3 } + ... $$
رابطه فوق بسیار آشنا به نظر میرسد. اگر تعدادی مقاومت به صورت موازی یکدیگر قرار بگیرند، مقاومت معادل یا موثر به صورت زیر بهدست میآید:
$$\frac { 1 } { R } = \frac { 1 } { R _ 1 } + \frac { 1 } { R_ 2 } + \frac { 1 } { R _ 3 } + ... $$
بنابراین، فنرهای سری مشابه مقاومتهای موازی عمل میکنند.
ثابت فنر در فنرهای موازی
فنرها ممکن است به صورت موازی در کنار یکدیگر قرار گرفته باشند. برای راحتی کار دو فنر با ثابتهای فنر $$k_1$$ و $$k_2$$ را در نظر میگیریم که به صورت موازی یکدیگر قرار دارند. این دو فنر را میتوانیم معادل یک فنر با ثابت فنر موثر K در نظر بگیریم. دو فنر موازی به صورت نشان داده شده در تصویر زیر به صورت موازی روی میز قرار گرفتهاند و نیروی F بر آنها وارد میشود.
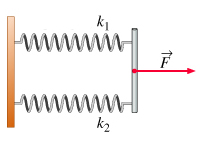
نیروی F بر هر دو فنر وارد میشود. شاید از خود بپرسید مقدار نیروی وارد شده بر هر فنر چه مقدار است. نیروی F بین دو فنر تقسیم میشود. بر فنر یک نیروی $$F_1$$ و بر فنر دو نیز نیروی $$F_2$$ وارد میشود:
$$F= F_ 1 + F _ 2$$
قانون هوک بدون علامت منفی به صورت زیر نوشته میشود:
$$F = k x $$
به جای هر یک از $$F$$ها در رابطه $$F= F_ 1 + F _ 2$$ رابطه $$F = k x $$ را قرار میدهیم:
$$KX = k_1 x_1 + k _ 2x _2$$
فرض میکنیم میزان کشیدگی دو فنر پس از اعمال نیروی F به آنها یکسان و برابر $$x$$ باشد، در نتیجه $$X = x_1 = x_2$$ و به راحتی میتوان آنها را از طرفین رابطه بالا حذف کرد:
$$K = k_ 1 + k_ 2$$
بنابراین، هنگامیکه فنرها به صورت موازی با یکدیگر قرار میگیرند، ثابت فنر معادل آنها از جمع جبری ثابتهای فنرها بهدست میآید. اگر بیشتر از دو فنر به صورت موازی به یکدیگر متصل شده باشند، ثابت فنر موثر آنها به صورت زیر بهدست میآید:
$$K = k_1 + k_2 + k_3 + ... $$
مثال اول
فنری را در نظر بگیرید که از سقف آویزان و جسمی به جرم m به آن متصل شده است. جسم را کمی به سمت پایین میکشیم و رها میکنیم. فنر و جسم با یکدیگر شروع به نوسان میکنند. در ادامه، فنری مشابه فنر اول را به انتهای آزاد آن وصل میکنیم. در این حالت دو فنر مشابه سری داریم. به انتهای این فنرِ سری، جسمی به جرم m متصل میکنیم. فنرها و جسم را کمی به سمت پایین میکشیم و رها میکنیم. مشابه حالت اول، فنرها و جسم با دوره تناوب مشخصی شروع به نوسان میکنند. دوره تناوب نوسان در حالت اول و دوم را بهدست آورید.
پاسخ
همانطور که در مطالب بالا اشاره شد دوره تناوب جسمی به جرم m که به انتهای فنری عمودی متصل شده است با استفاده از رابطه زیر بهدست میآید:
$$T = 2 \pi \sqrt { \frac { m } { k } }$$
در حالت اول یک فنر داریم که جرم m از آن آویزان شده و ثابت فنر برابر k است. دوره تناوب نوسان در این حالت برابر است با:
$$T_1 = 2 \pi \sqrt { \frac { m } { k } }$$
در حالت دوم، دو فنر داریم که جرم m از آن آویزان شده و ثابت فنر برابر K است. برای بهدست آوردن دوره تناوب نوسان ابتدا باید ثابت فنر معادل دو فنر را بهدست آوریم. فنرها به صورت سری با یکدیگر قرار گرفتهاند، بنابراین ثابت فنر معادل آنها با استفاده از رابطه زیر بهدست میآید:
$$\frac { 1 } { K } = \frac { 1 } { k _ 1 } + \frac { 1 } { k _ 2 } $$
$$k_1$$ و $$k_2$$ با یکدیگر برابر هستند و در نتیجه، ثابت فنر معادل برابر است با:
$$\frac { 1 } { K } = \frac { 1 } { k } + \frac { 1 } { k } \\ \frac { 1 } { K } = \frac { 2 } { k } \\ K = \frac { k } { 2 }$$
ثابت فنر معادل را در رابطه دوره تناوب قرار میدهیم:
$$T_2 = 2 \pi \sqrt { \frac { m } { \frac { k } { 2 } } } \\ T_1 = 2 \pi \sqrt { \frac { 2 m } { k } }$$
بنابراین، نسبت دوره تناوب حالت دوم به دوره تناوب حالت اول برابر است با:
$$\frac { T _ 2 } { T _ 1 } = \frac { 2 \pi \sqrt { \frac { 2 m } { k } } } { 2 \pi \sqrt { \frac { m } { k } } } = \sqrt { 2 }$$
مثال دوم
ثابت فنر معادل برای مجموعه فنرهای نشان داده شده در تصویر زیر را بهدست آورید.
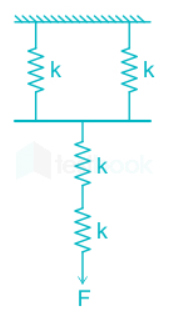
پاسخ
همانطور که در تصویر بالا مشاهده میکنید، فنرها به صورت سری و موازی به یکدیگر بسته شدهاند. ثابت فنر تمام فنرها با یکدیگر برابر است. ابتدا ثابت فنر معادل دو فنری را که به صورت موازی یکدیگر بسته شدهاند را بهدست میآوریم. همانطور که در مطالب بالا توضیح دادیم، ثابت فنر معادل دو فنر موازی با استفاده از رابطه زیر بهدست میآید:
$$k = k_1 + k_2$$
ثابت فنر هر یک از فنرها برابر k است، بنابراین ثابت دو فنر موازی برابر $$2k$$ خواهد بود. در نتیجه، به جای دو فنر موازی میتوانیم فنری با ثابت $$2k$$ قرار دهیم. این فنر با دو فنر دیگر به صورت سری به یکدیگر بسته شدهاند. از اینرو، سه فنر سری با ثابت فنرهای k و k و $$2k$$ داریم. ثابت فنر سه فنر سری با استفاده از رابطه زیر بهدست میآیند:
$$\frac { 1 } { K } = \frac { 1 } { k _ 1 } + \frac { 1 } { k _ 2 } + \frac { 1 } { k _ 3 }$$
بنابراین، ثابت فنر معادل برابر است با:
$$\frac { 1 } { K } = \frac { 1 } { k } + \frac { 1 } { k } + \frac { 1 } {2k} \\ \frac { 1 } { K } = \frac { 1 + 2 + 2 } { 2 k } \\ \frac { 1 } { K } = \frac { 5 } { 2 k } \\ K = \frac { 2 k } { 5 } = 0.4 \ k$$
مثال سوم
دو فنر با ثابتهای فنر ۱۰۰۰ و ۲۰۰۰ نیوتن بر متر به صورت موازی یکدیگر قرار گرفتهاند. ثابت فنر موثر آنها چه مقدار است؟
پاسخ
همانطور که در بخشهای قبل توضیح داده شد ثابت فنر موثر دو فنر موازی با استفاده از رابطه زیر بهدست میآید:
$$k = k_1 + k _ 2$$
در رابطه فوق:
- $$k$$ ثابت فنر موثر یا معادل برحسب نیوتن بر متر است.
- $$k_ 1$$ ثابت فنر فنرِ اول برحسب نیوتن بر متر است.
- $$ k_ 2 $$ ثابت فنرِ فنر دوم برحسب نیوتن بر متر است.
با قرار دادن مقدارهای داده شده در مثال، ثابت فنر موثر را بهدست میآوریم:
$$k = 1000 + 2000 = 3000 \ \frac { N } { m }$$
مثال چهارم
دو فنر با ثابتهای فنر ۱۰۰۰ و ۲۰۰۰ نیوتن بر متر داریم. در نخستین مرحله دو فنر را به صورت موازی با یکدیگر میبندیم. اگر جسمی به وزن ۱۰۰۰ نیوتن به این دو فنر متصل شود، میزان کشیدگی فنرها با یکدیگر چه مقدار است؟ در ادامه، فنرها به صورت سری به یکدیگر متصل میشوند. اگر جسم ۱۰۰۰ نیوتنی را به دو فنر متصل کنیم، میزان کشیدگی آنها را بهدست آورید.
پاسخ
در مرحله اول فنرها به صورت موازی با یکدیگر قرار میگیرند. ثابت فنر موثر دو فنر موازی با استفاده از رابطه زیر بهدست میآید:
$$k = k_1 + k_2$$
بنابراین، ثابت دو فنر با ثابتهای ۱۰۰۰ و ۲۰۰۰ نیوتن بر متر در حالت موازی برابر ۳۰۰۰ نیوتن بر متر است. میزان کشیدگی فنرها در این حالت برابر است با:
$$F = k x \\ x = \frac { F } { k } \\ x = \frac { 1000 } { 3000 } = 0.333 \ m$$
در ادامه، فنرها به صورت سری بسته میشوند. ثابت فنر موثر دو فنر سری با استفاده از رابطه زیر بهدست میآید:
$$\frac { 1 } { k } = \frac { 1 } { k _1 } + \frac { 1 } { k _ 2 }$$
در نتیجه، ثابت فنر موثر دو فنر موازی با ثابتهای فنر ۱۰۰۰ و ۲۰۰۰ نیوتن بر متر برابر است با:
$$\frac { 1 } { k } = \frac { 1 } { 1000 } + \frac { 1 } { 2000 } \\ \frac { 1 } { k } = \frac { 3 } { 2000 } \\ k = 666.7 \ \frac { N } { m }$$
میزان کشیدگی فنرها در این حالت برابر است با:
$$F = k x \\ x = \frac { F } { k } \\ x = \frac { 1000 } { 666.7 } = 1.50 \ m \ m$$
مثال پنجم
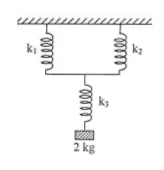
سه فنر با ثابتهای فنر برابر به صورت سری و موازی به یکدیگر متصل شدهاند. جسمی به جرم ۲ کیلوگرم را به صورت نشان داده شده در تصویر زیر از این فنرها آویزان میکنیم. اگر ثابت فنر هر یک از فنرها برابر ۳۰۰ نیوتن بر متر باشد، تغییر طول آنها چه مقدار خواهد بود؟ شتاب جاذبه زمین را ۱۰ متر بر مجذور ثانیه در نظر بگیرید.
پاسخ
در این مثال، ثابت هر فنر، جرم جسم، شتاب جاذبه زمین داده شدهاند. با استفاده از این دادهها میخواهیم تغییر طول مجموعه فنرها را بهدست آوریم. برای انجام این کار ابتدا باید ثابت موثر سه فنر محاسبه شود. فنرهای یک و دو به صورت موازی با یکدیگر قرار گرفتهاند. ثابت فنر معادل آنها برابر است با:
$$k _ { 1 2 }= k_1 + k_2 = 300 + 300 = 600 \ \frac { N } { m }$$
بنابراین، به جای فنرهای یک و دو میتوانیم فنری با ثابت فنر ۶۰۰ نیوتن بر متر قرار دهیم. این فنر به صورت سری با فنر سوم قرار میگیرد. ثابت فنر معادل این دو فنر به صورت زیر بهدست میآید:
$$\frac { 1 } { k } = \frac { 1 } { k_ { 1 2 } } + \frac { 1 } { k _ 3 } = \frac { 1 } { 300 } + \frac { 1 } { 600 } \\ \frac { 1 } { k } = \frac { 3 } { 600 } \\ k = 200 \ \frac { N } { m }$$
با داشتن ثابت فنر معادل، تغییر طول فنرها را به صورت زیر بهدست میآوریم:
$$\triangle x = \frac { F = mg } { k } = \frac { 2 \times 10 } { 200 } = 0.1 \ m$$
مثال ششم
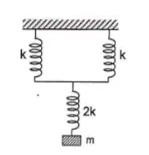
سه فنر به صورت سری و موازی به یکدیگر متصل شدهاند. جسمی به جرم ۴۰۰ گرم را به صورت نشان داده شده در تصویر زیر از این فنرها آویزان میکنیم. اگر مقدار k برابر ۵۰ نیوتن بر متر باشد، تغییر طول فنرها چه مقدار خواهد بود؟
پاسخ
در این مثال، ثابت هر فنر، جرم جسم، شتاب جاذبه زمین داده شدهاند. ثابت فنرهای یک، دو و سه به ترتیب برابر ۵۰، ۵۰ و ۱۰۰ نیوتن بر متر است. با استفاده از این دادهها میخواهیم تغییر طول مجموعه فنرها را بهدست آوریم. برای انجام این کار ابتدا باید ثابت موثر سه فنر محاسبه شود. فنرهای یک و دو به صورت موازی با یکدیگر قرار گرفتهاند. ثابت فنر معادل آنها برابر است با:
$$k _ { 1 2 }= k_1 + k_2 = 50 + 50 = 100 \ \frac { N } { m }$$
بنابراین، به جای فنرهای یک و دو میتوانیم فنری با ثابت فنر ۱۰۰ نیوتن بر متر قرار دهیم. این فنر به صورت سری با فنر سوم قرار میگیرد. ثابت فنر معادل این دو فنر به صورت زیر بهدست میآید:
$$\frac { 1 } { k } = \frac { 1 } { k_ { 1 2 } } + \frac { 1 } { k _ 3 } = \frac { 1 } { 100 } + \frac { 1 } { 100 } \\ \frac { 1 } { k } = \frac { 2 } { 100 } \\ k = 50 \ \frac { N } { m }$$
با داشتن ثابت فنر معادل، تغییر طول فنرها را به صورت زیر بهدست میآوریم:
$$\triangle x = \frac { F = mg } { k } = \frac { 0.4 \times 10 } { 50 } = 0.08 \ m$$
مثال هفتم
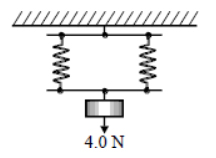
دو فنر با ثابت فنر یکسان به صورت موازی با یکدیگر قرار گفتهاند و جسمی به وزن ۴/۰ نیوتن از آنها آویزان شده است. اگر ثابت فنر هر فنر برابر ۲۰ نیوتن بر متر باشد، انرژی کشسانی ذخیره شده در سیستم چه مقدار است؟
پاسخ
انرژی کشسانی ذخیره شده در فنر با استفاده از رابطه زیر بهدست میآید:
$$U = \frac { 1 } { 2 } k x ^ 2$$
بنابراین، برای بهدست آوردن انرژی کشسانی سیستم نشان داده شده در تصویر بالا باید ثابت فنر معادل و تغییر طول مجموعه فنرها را بهدست آوریم. فنرها به صورت موازی با یکدیگر قرار گرفتهاند. ثابت فنر معادل آنها برابر است با:
$$k _ { 1 2 }= k_1 + k_2 = 20 + 20 = 40 \ \frac { N } { m }$$
با داشتن ثابت فنر معادل، تغییر طول فنرها را به صورت زیر بهدست میآوریم:
$$\triangle x = \frac { F = mg } { k } = \frac { 4/0 } { 40 } = 0.1 \ m$$
با داشتن تغییر طول فنرها و ثابت فنر معادل، انرژی کشسانی را بهدست میآوریم:
$$U = \frac { 1 } { 2 } k x ^ 2 \\ U = \frac { 1 } { 2 } \times 40 \times (0.1) ^ 2 = 0.2 \ J$$
مثال هشتم
دو فنر با ثابتهای فنر ۳۰۰ و ۶۰۰ نیوتن بر متر به صورت افقی و سری به یکدیگر متصل شدهاند. جسمی به جرم ۲ کیلوگرم به آنها متصل میشود. فنرها و جسم ابتدا در حالت تعادل قرار دارند. جسم را کمی از حالت تعادل میکشیم و آن را رها میکنیم. فنرها و جسم با یکدیگر شروع به نوسان میکنند. فرکانس زاویهای نوسان چه مقدار است؟
پاسخ
فنرها به صورت سری به یکدیگر متصل شدهاند. ثابت فنر معادل این دو فنر به صورت زیر بهدست میآید:
$$\frac { 1 } { k } = \frac { 1 } { k_ 1 } + \frac { 1 } { k _ 2 } = \frac { 1 } { 300 } + \frac { 1 } { 600 } \\ \frac { 1 } { k } = \frac { 3 } { 600 } \\ k = 200 \ \frac { N } { m }$$
فرکانس زاویهای حرکت هماهنگ ساده با استفاده از رابطه زیر بهدست میآید:
$$\omega = \sqrt {\frac { k } { m } }\\ \omega = \sqrt { \frac { 200 } { 2 } } \\ \omega = 10 \ \frac { rad } { s }$$
مثال نهم
در آزمایشگاه فیزیک پایه یک دو فنر با ثابتهای فنر متفاوت به صورت موازی به یکدیگر وصل شدهاند. ثابت فنر معادل فنرها برابر ۸۰۰ نیوتن بر متر است. اگر ثابت فنر یکی از فنرها برابر ۴۰۰ نیوتن بر متر باشد، ثابت فنرِ فنر دوم را بهدست آورید.
پاسخ
فنرها به صورت موازی با یکدیگر قرار گرفتهاند. ثابت فنر معادل آنها با استفاده از رابطه زیر بهدست میآید:
$$k _ { 1 2 }= k_1 + k_2 $$
$$k_ { 1 2 }$$ و $$k_1$$ را داریم، بنابراین به راحتی میتوانیم $$k_2$$ را بهدست آوریم:
$$800 = 400 + k_2 \\ k_ 2 = 800 - 400 = 400 \ \frac { N } { m }$$
مثال دهم
فنری با ثابت فنر ۱۵۰۰ نیوتن بر متر به صورت عمودی به سقف وصل شده است. جسمی به جرم ۲ کیلوگرم به انتهای آزاد فنر متصل و سبب کشیدن فنر میشود. سپس، فنر مشابهی را به صورت سری به فنر اول متصل و جسم به جرم دو کیلوگرم را از مجموعه دو فنر سری آویزان میکنیم. نسب میزان کشیدگی فنرها در حالت دوم به میزان کشیدگی فنر در حالت اول برابر است با:
دو
سه
یک
چهار
برای حل این مثال گامهای زیر را به ترتیب طی میکنیم:
- ابتدا تغییر طول فنر اول قبل از اتصال فنر دوم به آن را بهدست میآوریم.
- سپس، ثابت فنر معادل دو فنر سری را بهدست میآوریم.
- تغییر طول کلی دو فنرِ سری را بهدست میآوریم.
در ابتدا فنری با ثابت فنر ۱۵۰۰ نیوتن بر متر داریم که به صورت عمودی به سقف وصل و جسمی به جرم ۲ کیلوگرم به انتهای آزاد آن وصل شده است. فنر پس از اتصال جسم ۲ کیلوگرمی به اندازه $$\triangle x_1$$ کشیده میشود:
$$\triangle x_ 1 = \frac { m g } { k } \\ \triangle x_ 1 = \frac { 2 \times 9.8 } { 1500 } = 0.013 \ m$$
در نتیجه، میزان کشیدگی دو فنر سری در حالت دوم، دو برابر میزان کشیدگی تک فنر در حالت اول است.
در ادامه، فنر دوم را به صورت سری به فنر اول متصل و جسمی به جرم ۲ کیلوگرم به مجموعه دو فنر سری متصل میکنیم. برای بهدست آوردن تغییر طول سیستم فنرها در این حالت، ابتدا باید ثابت فنر معادل را بهدست آوریم. ثابت فنر معادل دو فنر سری به صورت زیر بهدست میآیند:
$$\frac { 1 } { k } = \frac { 1 } { k_ 1 } + \frac { 1 } { k _ 2 } \\ \frac { 1 } { k } = \frac { 1 } { 1500 } + \frac { 1 } { 1500 } = \frac { 2 } { 1500 } \\ k = 750 \ \frac { N } { m }$$
در حالت دوم به جای دو فنر سری، فنری با ثابت فنر معادل ۷۵۰ نیوتن بر متر قرار میدهیم و کشیدگی آن، $$\triangle x _2$$، را بهدست میآوریم:
$$\triangle x_ 2 = \frac { m g } { k } \\ \triangle x_ 1 = \frac { 2 \times 9.8 } { 750 } = 0.026 \ m$$
مثال یازدهم
سه فنر با ثابتهای فنر $$k_1 = 200 \ \frac { N } { m }$$ و $$k_2 = 400 \ \frac { N } { m }$$ و $$k_3 = 600 \ \frac { N } { m }$$ به صورت عمودی و موازی به یکدیگر وصل شدهاند. جسمی به جرم ۰/۵ کیلوگرم را از مجموعه فنرها آویزان میکنیم، بنابراین، فنرها و جسم به صورت عمودی شروع به نوسان میکنند. فرکانس نوسان چه مقدار است؟
۸/۸ هرتز
۷/۸ هرتز
۶/۸ هرتز
۵/۸ هرتز
فنرها به صورت موازی با یکدیگر قرار گرفتهاند، بنابراین ثابت فنر معادل آنها با استفاده از رابطه $$k = k_1 + k_2 + k_3$$ بهدست میآید:
$$k = 200 + 400 + 600 = 1200 \ \frac { N } { m }$$
به جای سه فنر موازی میتوانیم فنری با ثابت فنر معادل ۱۲۰۰ نیوتن بر متر قرار دهیم که جسمی به جرم ۰/۵ کیلوگرم به انتهای آن وصل شده است. فنر و جرمِ متصل به آن با فرکانس مشخصی شروع به نوسان میکنند. برای بهدست آوردن فرکانس نوسان، ابتدا فرکانس زاویهای نوسان، یعنی $$\omega$$، را بهدست میآوریم:
$$\omega = \sqrt { \frac { k } { m } } \\ \omega = \sqrt { \frac { 1200 } { 0.5 } } \\ w \sim 49 \ \frac { rad } { s }$$
فرکانس و فرکانس زاویهای نوسان با استفاده از رابطه زیر به یکدیگر مربوط میشوند:
$$f = \frac{ \omega } { 2 \ pi } \\ f= \frac { 794 } { \pi} \\ f = 7.8 \ Hz $$
مثال دوازدهم
دو فنر با ثابتهای فنر ۱۰۰ و ۲۰۰ نیوتن بر متر به صورت سری به یکدیگر متصل و از سقف آویزان شدهاند. جسمی به جرم یک کیلوگرم را به انتهای مجموعه فنرها وصل و آن را به اندازه ۲۰ سانتیمتر به سمت پایین میکشیم و رها میکنیم. بیشینه سرعت جسم به هنگام نوسان برابر است با:
۰/۱۶ متر بر ثانیه
۰/۰۴ متر بر ثانیه
۱/۶ متر بر ثانیه
۰/۸۲ متر بر ثانیه
سرعت بیشینه نوسان جسم متصل به فنرها با استفاده از رابطه زیر بهدست میآید:
$$V_ { max } = A \omega$$
در رابطه فوق:
- $$A$$ دامنه نوسان است.
- $$\omega$$ فرکانس زاویهای نوسان است.
بنابراین، برای بهدست آوردن بیشینه سرعت نوسان باید فرکانس زاویه و دامنه نوسان را بهدست آوریم. ابتدا فرکانس زاویهای را بهدست میآوریم. برای بهدست آوردن $$\omega$$ باید ثابت فنر معادل را محاسبه کنیم. فنرها به صورت سری به یکدیگر متصل شدهاند. از اینرو، ثابت فنر معادل آنها به صورت زیر بهدست میآید:
$$\frac { 1 } { k } = \frac { 1 } { k_1 } + \frac { 1 } { k _ 2 } \\ \frac { 1 } { k } = \frac { 1 } { 100 } + \frac { 1 } { 200 } \\ k = 66.7 \ \frac { N } { m }$$
فرکانس زاویهای نوسان برابر است با:
$$\omega = \sqrt { \frac { k } { m } } \\ \omega = \sqrt { \frac { 66.7 } { 1 } } \\ \omega \sim 8.2 \ \frac { rad } { s } $$
دامنه نوسان برابر نصف جابجایی کل است:
$$A = \frac { 0.2 \ m } { 2 } = 0.1 \ m$$
در نتیجه، سرعت بیشینه نوسان برابر است با:
$$V_ { max} = A \omega = 0.1 \times 8.2 = 0.82 \ \frac { m } {s } $$
مثال سیزدهم
گروهی از دانشجویان موسیقی برای انجام پروژه دانشگاهی خود باید ساز موسیقی منحصربهفردی را با استفاده از فنرهای نوسانکننده طراحی کنند. آنها برای انجام این کار میخواهند فنرها با ثابتهای فنر متفاوت را با یکدیگر ترکیب کنند. اگر دانشجویان برای ساخت ساز موسیقی خود سه فنر با ثابتهای فنر ۲۰۰، ۳۵۰ . ۵۰۰ را به صورت موازی به یکدیگر و جسمی به جرم ۰/۲ کیلوگرم را به آنها متصل کنند، فرکانس اصلی صدای تولید شده توسط این ساز چه مقدار خواهد بود؟
۱۰/۵ هرتز
۹ هرتز
۱۲ هرتز
۱۱/۵ هرتز
فنرها به صورت موازی به یکدیگر متصل شدهاند. از اینرو، ثابت فنر معادل آنها به صورت زیر بهدست میآید:
$$k = k_1 + k_2 + k_3 = 200 + 350 + 500 = 1050 \ \frac { N } { m } $$
فرکانس زاویهای نوسان برابر است با:
$$\omega = \sqrt { \frac { k } { m } } \\ \omega = \sqrt { \frac { 1050 } { 0.2 } } \\ \omega \sim 72.46 \ \frac { rad } { s } $$
فرکانس بنیادی نت موسیقی تولید شده توسط ساز موسیقی به صورت زیر با فرکانس زاویهای رابطه دارد:
$$f = \frac { \omega} { 2 \pi}$$
بنابراین، f برابر ۱۱/۵ هرتز بهدست میآید.
مثال پانزدهم
چهار فنر به صورت نشان داده شده در تصویر زیر به جسمی به جرم m متصل شدهاند. اگر جسم را به اندازه ۰/۰۵۹ متر از حالت تعادل به سمت پایین بکشیم و رها کنیم، نیروی وارد شده از سمت فنرها بر جسم در نقطه رها شدن، چه مقدار است؟ 
۰/۶۶ نیوتن
۱/۸ نیوتن
۰/۸۹ نیوتن
۱/۰ نیوتن
چهار فنر با ثابتهای فنر ۶۵، ۳۰، ۴۸ و ۵۲ نیوتن بر متر به صورت سری قرار گرفتهاند. همانطور که میدانیم ثابت فنر معادل فنرهای موازی با استفاده از رابطه زیر بهدست میآید:
$$\frac { 1 } { k } = \frac { 1 } { k_ 1 } + \frac { 1 } { k_ 2 } + \frac { 1 } { k_ 3 } + \frac { 1 } { k_ 4 }$$
ثابتهای فنر هر یک از فنرها را در رابطه بالا قرار میدهیم و ثابت فنر معادل را بهدست میآوریم:
$$\frac { 1 } { k } = \frac { 1 } { 65 } + \frac { 1 } { 30 } + \frac { 1 } { 48 } + \frac { 1 } { 52 } \\ k \sim 11.3 \ \frac { N } { m }$$
با بهدست آوردن ثابت فنر معادلِ چهار فنر سری، میتوانیم چهار فنر را با فنری با ثابت فنر ۱۱/۳ نیوتن بر متر جایگزین کنیم. برای بهدست آوردن مقدار نیروی فنر از قانون هوک استفاده میکنیم:
$$F = K \triangle x \\ F = 11.3 \times 0.059 = 0.66 \ N$$
ثابت فنر چرخشی
فنر چرخشی درامتداد محور فنر پیچ خورده است. پیچ خوردن در امتداد محور فنر به معنای وارد شدن نیرویی در خلاف جهت پیچش و متناسب با زاویه پیچش است. فنرهای پیچشی در محدوده حد کشسانی از قانون هوک پیروی میکنند:
$$T = - \ K \theta $$
در رابطه فوق $$K$$ ثابت فنر پیچشی و یکای اندازهگیری آن برابر نیوتن-متر بر رادیان و T گشتاور وارد شده توسط فنر و یکای اندازهگیری آن نیوتن-متر است. همچنین، $$\theta$$ مقدار زاویه پیچشی از حالت خواهد بود.
جمعبندی
در این مطلب، در مورد ثابت فنر صحبت کردیم. به مقاومت فنر در برابر تغییر شکل، کشیدن یا فشرده شدن، سختی یا ثابت فنر گفته میشود. جنس مادهای که فنر از آن ساخته میشود، تعداد سیمپیچهای فعال و طول آزاد فنر بدون اتصال جسم خارجی به آن از مهمترین عاملهای موثر بر مقدار ثابت فنر هستند.
ثابت فنر با استفاده از قانون هوک، به صورت زیر بهدست میآید:
$$F = - \ k x$$
بر طبق این رابطه، نیرو و جابهجایی فنر از حالت تعادل با یکدیگر رابطه خطی دارند. به این نکته توجه داشته باشدی که این رابطه خطی تا وقتی برقرار است فنر پس از کشیده یا فشرده شدن بتواند به طول طبیعی خود بازگردد. فنرها ممکن است به صورت سری در کنار یکدیگر قرار گرفته باشند. سری وصل شدن فنرها بدان معنا است که به صورت متوالی و به دنبال یکدیگر قرار گرفتهاند. اگر بیشتر از دو فنر به صورت سری به یکدیگر متصل شده باشند، ثابت فنر موثر آنها به صورت زیر بهدست میآید:
$$\frac { 1 } { K } = \frac { 1 } { k _ 1 } + \frac { 1 } { k _ 2 } + \frac { 1 } { k _ 3 } + ... $$
فنرها ممکن است به صورت موازی در کنار یکدیگر قرار گرفته باشند. هنگامیکه فنرها به صورت موازی با یکدیگر قرار میگیرند، ثابت فنر معادل آنها از جمع جبری ثابتهای فنرها بهدست میآید. اگر بیشتر از دو فنر به صورت موازی به یکدیگر متصل شده باشند، ثابت فنر موثر آنها به صورت زیر بهدست میآید:
$$K = k_1 + k_2 + k_3 + ... $$
