تابع حالت ترمودینامیکی – از صفر تا صد
در علم ترمودینامیک، یک تابع حالت به تابعی تعریف شده در سیستم میگویند که مقادیر مختلف متغیرهای حالت را به یکدیگر مرتبط میکند. تابع حالت به مسیر فرآیند طی شده توسط سیستم ارتباطی ندارد. این تابع، حالت تعادلی یک سیستم و نوع آنرا توصیف میکند. به طور مثال، یک تابع حالت، اتم یا مولکول را در گاز، مایع یا جامد توصیف میکند. همچنین میتواند به توصیف مخلوط همگن یا غیرهمگن و مقدار انرژی مورد نیاز برای ایجاد چنین سیستمی بپردازد. در مثالی دیگر میتوان به انرژی درونی، آنتالپی و آنتروپی اشاره کرد که هر سه، توابع حالت هستند چراکه به صورت کمی، حالت تعادل یک سیستم ترمودینامیکی را توصیف میکنند. در مقابل، کار و گرما، مقادیر فرآیندی یا تابع مسیر هستند زیرا مقدار آنها به مسیر ویژه گذر بین دو حالت تعادلی وابسته است.

گرما اگر به صورت گسسته در نظر گرفته شود، نوعی تابع حالت همچون آنتالپی را میتواند توصیف کند اما به طور کلی، توانایی توصیف یک سیستم را به شکل حقیقی ندارد مگر اینکه به صورت تابع حالت یک سیستم خاص توصیف شود. شرایط مشابهی نیز به هنگام مقایسه گرما با دما بوجود میآید. در این آموزش قصد داریم تا در خصوص اهمیت تابع حالت بودن انرژی و مقایسه آن با کار و گرما به عنوان توابع مسیر، به بحث بپردازیم.
تابع حالت و تابع مسیر
در بیان دیگری از قانون اول ترمودینامیک، اینطور میتوان گفت که تغییرات انرژی درونی، مستقل از مسیر فرآیند طی شده از حالت اولیه به حالت نهایی است و تنها به حالتهای اولیه و نهایی بستگی دارد. چنین تعریفی را برای انرژی جنبشی در نظر میگیریم که میتواند به سایر شکلهای انرژی گسترش پیدا کند.
یک مولکول تنها را در سیستم در نظر بگیرید. تصور کنید که این مولکول با جرم m، دارای سرعت اولیه است. حال این سرعت را به صورت گام به گام به شکل افزایش میدهیم. تغییرات انرژی جنبشی به صورت زیر خواهد بود:
با وجود اینکه مقادیر و ، هر مقداری را میتوانند اختیار کنند اما مقادیر آنها بر نتیجه نهایی بیتاثیر است. به این نتیجه میرسیم که تغییرات انرژی جنبشی، تنها به سرعتهای اولیه و نهایی بستگی دارند و مستقل از مسیر انجام شده بین این دو سرعت هستند. حتی اگر تعداد گامهای سرعت را نیز افزایش دهیم، باز به همین نتیجه میرسیم. از آنجایی که این نتیجه، برای تمامی مولکولهای موجود در سیستم صدق میکند، در نتیجه برای تغییرات انرژی درونی هم میتوان این نتیجه را تصدیق کرد.

تابع حالت
مثال بالا، این ادعا را ثابت میکند که تغییرات انرژی درونی، تنها به حالتهای اولیه و نهایی وابسته است و به مسیر رسیدن به این دو حالت بستگی ندارد. هر تابعی که چنین شرایطی داشته باشد، موسوم به «تابع حالت» (State Function) است چراکه تنها به حالت سیستم و نه مسیر رسیدن به آن حالت، بستگی دارد. در هر تابع حالتی، به طور مثال ، چنین رابطهای صدق میکند:
دیفرانسیل کامل
در رابطه بالا، i و f به ترتیب نشاندهنده حالات اولیه و نهایی هستند. این رابطه نشان میدهد بمنظور اینکه تنها به حالات اولیه و نهایی وابسته باشد، مقدار انتگرال باید مستقل از مسیر فرآیند در نظر گرفته شود. اگر چنین شرایطی برقرار باشد، را میتوان به صورت یک جزء بسیار کوچک تعریف کرد که با انتگرالگیری، مقدار آن تنها به حالات اولیه و نهایی بستگی دارد. مقدار موسوم به «دیفرانسیل کامل» (Exact Differential) است. بهتر است که در این خصوص یک «انتگرال مسیر» (Cyclic Integral) تعریف کنیم که به یک مسیر دورانی اشاره دارد و در آن، حالات اولیه و نهایی برابر هستند. برای یا هر تابع حالت دیگری، رابطه زیر را میتوان ارائه داد و جواب این انتگرال، همانطور که مشاهده میکنید برابر با صفر است زیرا در این انتگرال، حالات اولیه و نهایی با یکدیگر برابرند:
تابع مسیر
در ادامه نشان میدهیم که و کار در ترمودینامیک، توابع حالت نیستند. حالت یک سیستم تکفاز با اجزای ثابت، به کمک دو متغیر از سه متغیر فشار، دما و حجم، مشخص میشود. همین امر برای انرژی درونی هم صدق میکند.
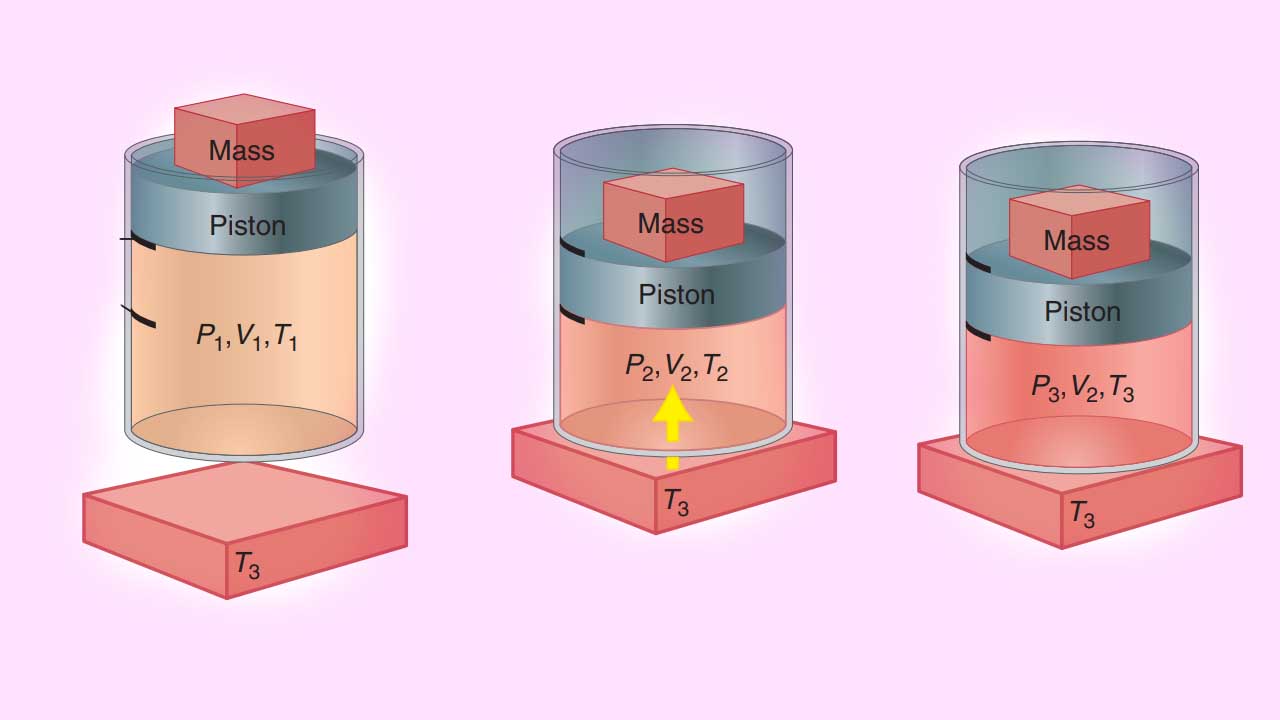
بنابراین، برای یک سیستم با جرم ثابت، را به میتوان به هر سه شکل ، یا نشان داد. فرض کنید گازی با حجم و فشار و در یک سیستم سیلندر و پیستون محبوس شده باشد. یک منبع حرارتی در محیط با دمای داریم. با انجام کار بر روی سیستم، حجم اولیه به حالت واسط میرسد که در آن، است. کار انجام شده، به صورت زیر محاسبه میشود:
از آنجایی که در تصویر زیر، به هنگام تراکم، کار بر روی سیستم انجام شده است، مقدار w مثبت خواهد بود و افزایش پیدا میکند. به دلیل اینکه سیستم تکفاز داریم، تابع یکنوا است و هم افزایش پیدا میکند. در ادامه، پیستون را در محل خود ثابت میکنیم و فرصت میدهیم تا حرارت در حجم ثابت، بین سیستم و محیط جریان پیدا کند. این کار را با تماس سیستم با منبع حرارتی انجام میدهیم. مقادیر دما و حجم در حالت نهایی و بعد از این دو گام، برابر با و خواهند بود.
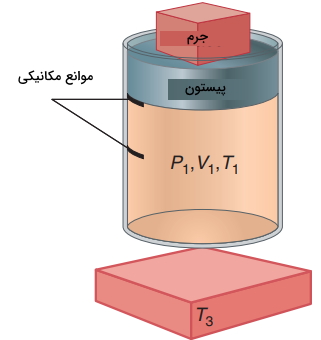
این دو گام را با مقادیر متفاوت از فشار خارجی، به کمک تغییر جرم روی پیستون تکرار میکنیم. در هر حالت، سیستم در حالت نهایی خود با همان متغیرهای و مشخص میشود. گامهایی که سیستم را از حالت اولیه به حالت نهایی و میرسانند با نام «مسیر» (Path) شناخته میشوند. با تغییر جرم، دستهای مسیر متفاوت ایجاد خواهد شد که همگی از حالتهای اولیه نشأت میگیرند و به حالت نهایی میرسند. بر اساس قانون اول ترمودینامیک، تغییرات انرژی برای این دو گام به صورت زیر تعریف میشود:
از آنجایی که تابع حالت به شمار میآید، مقدار آن برای فرآیند دو مرحلهای با فرآیند چند مرحلهای بالا یکسان است. اما سوالی که در اینجا مطرح میشود این است که آیا و نیز تابع حالت هستند یا خیر؟ برای یک فرآیند دو مرحلهای خواهیم داشت:
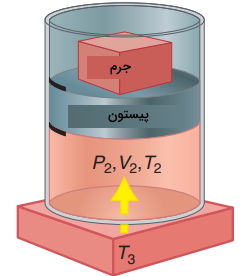
در رابطه بالا، تغییرات حجم ثابت است اما میزان فشار خارجی برای هر مقدار از جرم یا برای هر مسیر، تفاوت دارد. بنابراین، مقدار نیز در هر مسیر، متفاوت خواهد بود. با توجه به اینکه مقدار کار محاسبه شده در هر مسیر با یکدیگر تفاوت دارد، انتگرال مسیر برای کار، برابر با صفر نخواهد بود. در نتیجه، یک تابع حالت نیست. برای محسابه در هر مسیر، از قانون اول ترمودینامیک بهره میگیریم که رابطه آن در زیر نشان داده شده است:
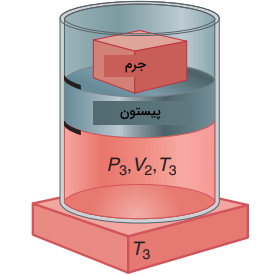
از آنجایی که مقدار در هر مسیر یکسان ولی مقدار متفاوت است، نتیجه میگیریم که نیز در هر مسیر مقدار متفاوتی دارد. همچون کار، انتگرال مسیر برای نیز مقدار صفر نخواهد داشت. بنابراین، و ، هیچکدام توابع حالت نیستند بلکه هر دو تابع مسیر هستند. به همین دلیل، بدون تعریف مسیر، هیچ دیفرانسیل کاملی را برای گرما و کار نمیتوان تعریف کرد و مقادیر دیفرانسیلی را برای این توابع، به صورت و نشان نمیدهند. به دلایلی که گفته شد، مقادیری همچون ، یا و همچنین مقادیر ، یا برای کار و گرما تعریف نمیشوند. در حقیقت، یک سیستم نمیتواند دارای کار یا گرما باشد بلکه بعد از انتقال کامل کار یا گرما بین سیستم و محیط، سیستم و محیط، انرژی درونی خواهند داشت نه گرما و کار.
بحثی که در بالا مطرح شد بر این نکته تاکیید دارد که عبارات کار و گرما را به گونهای بکار ببریم که نشان دهند تابع حالت نیستند. سیستمهایی که به طور معمول در علم شیمیفیزیک مورد بررسی قرار میگیرند عبارتند از:
در هریک از سیستمهایی که ذکر شد، آنچه اهمیت دارد، جریان کار یا گرما بین سیستم و محیط است. به طور مثال، در یک یخچال، از انرژی الکتریکی بمنظور استخراج حرارت از داخل دستگاه و آزادسازی آن در محیط استفاده میشود. میتوان گفت که یخچال، دستگاهی است که گرما را استخراج میکند اما اینکه بگوییم یخچال، دستگاهی دارای گرما است، جمله صحیحی نیست. در یک موتور درونسوز، انرژی شیمیایی که پیوندها در مولکولهای سوخت و اکسیژن دارند، برای تشکیل دیاکسید کربن و بخار آب آزاد میشوند. از این تغییر در انرژی درونی میتوان برای حرکت خودرو و چرخاندن چرخهای آن استفاده کرد. در نتیجه، در اینجا، جریانی از کار بین خودرو و محیط خواهیم داشت. به طور مشابه، میتوان گفت که موتور خودرو توانایی انجام کار دارد اما نمیتوان گفت که خودرو یا موتور، شامل کار هستند.
اگر این مطلب برای شما مفید بوده است، آموزشها و مطالب زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای دروس شیمی
- مجموعه آموزشهای مهندسی شیمی
- آموزش ترمودینامیک مهندسی شیمی
- فوگاسیته چیست؟ — به زبان ساده
- اکتیویته در شیمی — از صفر تا صد
- جدول تناوبی — از صفر تا صد
^^












