فضای باناخ و خصوصیات آن — به زبان ساده
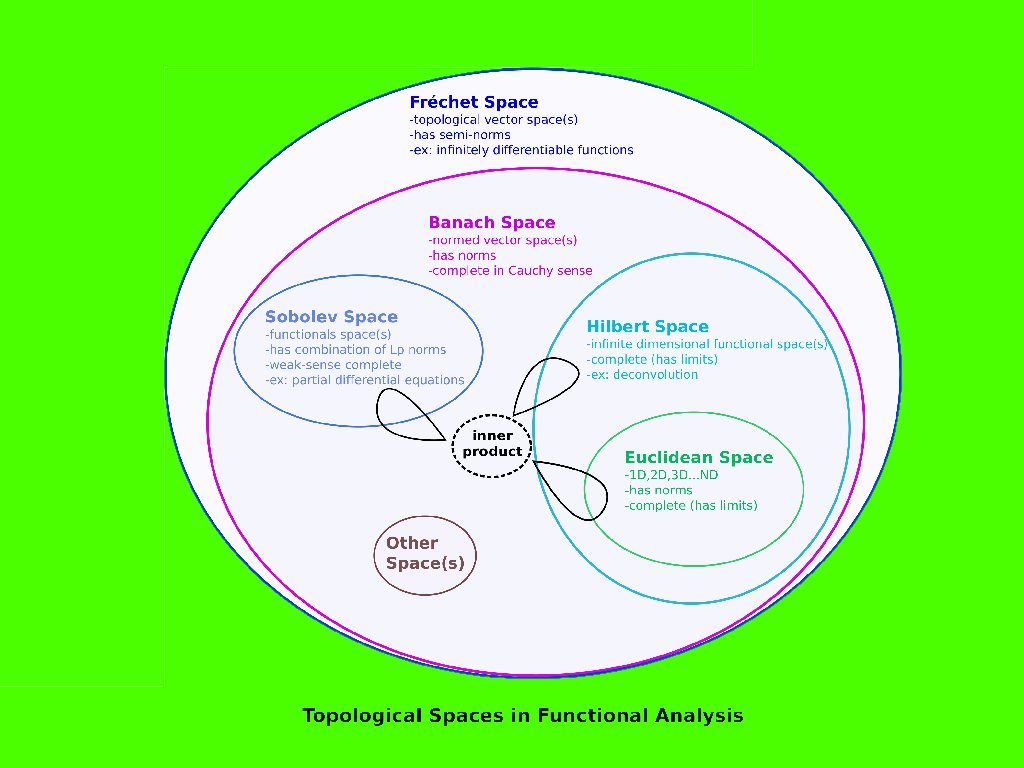
در ریاضیات و بخصوص آنالیز تابعی (Functional Analysis)، فضای باناخ (Banach Space) از اهمیت ویژهای برخوردار است. فضای باناخ در حقیقت یک «فضای برداری کامل نرمدار» (Complete Normed Vector Space) است. این امر به این معنی است که در فضای باناخ، میتوان به کمک یک متر (Meter) طول هر بردار را اندازهگیری کرد. به همین ترتیب فاصله بین دو بردار نیز به کمک تابع فاصله (نرم) قابل محاسبه خواهد بود. از طرفی این فضا، کامل است، یعنی دنبالهای کوشی از بردارها در این فضا دارای حد است. این ویژگیها باعث شده است به بررسی فضای باناخ و خصوصیات آن بپردازیم.
آنالیز تابعی، بخشی و شاخهای از دانش ریاضیات است که به بررسی توابع ریاضی (Functions) و عملگرها (Operators) اعمال شده روی این توابع میپردازد. واضح است که هر مجموعه به همراه یک عملگر تشکیل یک فضا را میدهد. از آنجایی که توابع را میتوان به صورت مجموعههایی در نظر گرفت، در نتیجه میتوان «آنالیز تابعی» (Functional Analysis) را دانشی مربوط به تحلیل فضاهای ریاضیاتی در نظر گرفت.
تبدیل فوریه، معادلات دیفرانسیل، معادلات انتگرالی، فضای باناخ و فضای هیلبرت از موضوعاتی هستند که در آنالیز تابعی به آنها پرداخته میشود.
برای آشنایی بیشتر با اصطلاحات به کار رفته در این زمینه، به عنوان مقدمه بهتر است نوشتارهای فضای اقلیدسی و خصوصیات آن — به زبان ساده و فضای هیلبرت و خصوصیات آن را مطالعه کنید. همچنین خواندن ضرب داخلی بردارها — به زبان ساده و فضای متریک و نامساوی مثلثی — به زبان ساده نیز خالی از لطف نیست.
فضای باناخ و خصوصیات آن
فضای باناخ، نقش اصلی را در آنالیز تابعی ایفا میکند حتی در آنالیزهای دیگر نیز بیشتر فضاهای مورد استفاده، فضای باناخ هستند. این فضا به افتخار ریاضیدان لهستانی «استفان باناخ» (Stefan Banach) که اولین بار در سالهای ۱۹۲۰ تا ۱۹۲۲ به این موضوع پرداخت، نامگذاری شده است.
در این بین همکارانی مانند «هانس هان» (Hans Hahn) و «ادوارد هلی» (Eduard Helly) او را همراهی کردند.

فضای باناخ براساس مطالعاتی که دیوید هیلبرت (David Hilbert) در فضای ضرب داخلی انجام داد، پدید آمد. در ادامه به تعریف فضای باناخ و خصوصیات آن خواهیم پرداخت. البته کاربردهایی نیز از این فضای ضرب داخلی معرفی میکنیم.

فضای باناخ
به یاد دارید که یک مجموعه به همراه یک عملگر، میتواند یک فضا تشکیل دهد. به همین ترتیب، فضای باناخ، یک فضای ضرب داخلی برداری است. این امر به این معنی است که براساس بردارها و عمل ضرب داخلی آنها، فضای باناخ تعریف میشود.
به این ترتیب میتوان فضای باناخ را به صورت یک فضای برداری ($$ X $$) روی میدان $$ K $$ به همراه یک نُرم یا اندازه به شکل $$ || \cdot ||_X $$ معرفی کرد. این نُرم میتواند به عنوان یک تابع فاصله عمل کند در نتیجه این فضا نسبت به آن نُرم یک فضای کامل (Complete) خواهد بود. بر این اساس برای هر دنباله کوشی به شکل $$ \{x_n\} $$ در $$ X $$ عنصری مانند $$ x $$ در این فضا وجود دارد که رابطه زیر برایش برقرار است.
$$ \large \lim _{n\to \infty }x_{n} = x $$
البته رابطه بالا را به صورت همارز به شکل زیر نیز میتوان نشان داد.
$$ \large \lim _{n\to \infty }\left\|x_{n} - x \right\|_{X} = 0 $$
نکته: میدان $$K$$ میتواند میدان حاصل از مجموعه اعداد حقیقی یا اعداد مختلط باشد.
وجود ساختار فضای برداری به ما این اجازه را میدهد که رفتار دنباله کوشی را به صورت همگرایی دنبالهای از بردارها در نظر بگیریم. فضای نرمدار (فضای اندازه) $$ X $$ در این حالت یک فضای باناخ است اگر و فقط اگر هر دنباله مطلقا همگرا در $$X$$، همگرا در $$ X $$ نیز باشد. این امر در رابطه زیر نشان داده شده است.
$$ \large \sum _{n = 1}^{ \infty }\| v_{n} \|_{X} < \infty \quad { \text{ implies that }} \quad \sum _{n = 1}^{ \infty } v_{n}\ \ { \text{ converges in }}\ \ X$$
نکته: کامل بودن فضای نرمدار با جایگزینی اندازه (نرم) با یک نرم همارز، حفظ میشود.
از آنجایی که همه نُرمها در فضای برداری با ابعاد متناهی، معادل و همارز هستند، در نتیجه هر فضای نرمدار با ابعاد متناهی روی اعداد حقیقی یا اعداد مختلط، یک فضای باناخ خواهد بود.
توجه داشته باشید که دو نرم $$ p $$ و $$ q $$ در فضای برداری $$ X $$، همارز هستند اگر برای هر دو ثابت $$ c $$ و $$ C $$ داشته باشیم:
$$ \large \forall v \in V, \exists c > 0 , c q ( V ) \leq p ( V ) \leq C q ( V ) $$
عملگرهای خطی و همریختی در فضای باناخ
فرض کنید $$X$$ و $$Y$$ دو فضای نرمدار روی میدان $$K$$ باشند. آنگاه مجموعه تمامی نگاشتهای پیوسته $$K$$-خطی ($$K$$-linear) که به صورت $$T: X \rightarrow Y $$ نوشته میشوند را به شکل $$B(X,Y)$$ نشان میدهیم.
در فضای با ابعاد نامتناهی هر نگاشت خطی لزوما پیوسته نیست. در این حالت نگاشت از یک فضای نرمدار مثال $$X$$ به فضای نرمدار دیگر مثل $$Y$$ پیوسته است اگر و فقط اگر این نگاشت، روی هر گوی واحد بسته (Closed Unit Ball) از $$X$$، کراندار باشد. در این حالت فضای برداری $$B(X,Y)$$ میتواند یک عملگر نُرم در نظر گرفته شود. در حقیقت برای تبدیل $$T$$ داریم:
$$ \large \|T\|=\sup \left\{\|Tx\|_{Y}\mid x\in X,\ \|x\|_{X}\leq 1\right\}$$
در این حالت، برای فضای باناخ $$Y$$، فضای $$B(X,Y)$$ یک فضای باناخ نسبت به نرم تعریف شده $$||T||$$ است. همچنین اگر $$X$$ یک فضای باناخ باشد، فضای $$B(X) = B(X,X)$$ یک «جبر باناخ» (Banach Algebra) تشکیل میدهد که در آن عملگر ضرب بوسیله ترکیب خطی از نگاشتها خواهد بود.
این بار دو فضای نرمدار $$X$$ و $$Y$$ را در نظر بگیرید که بینشان یک نگاشت خطی دو طرفه (یک به یک و پوشا) مثل $$T$$ وجود دارد. در این صورت اگر $$T: X \rightarrow Y $$ باشد، آنگاه $$T^{-1}$$ نیز وجود داشته و به شکل $$T^{-1}: Y \rightarrow X$$ است.
با وجود این فرضیات، دو فضای $$X$$ و $$Y$$ را «همریخت» (Isomorphic) میگویند، اگر $$T$$ و $$T^{-1}$$ پیوسته باشند. به علاوه اگر یکی از دو فضای $$X$$ یا $$Y$$ کامل باشند یا به معنی معادل انعکاسی (Reflexive) و جداپذیر (Separable) و ... باشد، آنگاه فضای دیگر نیز کامل است.
دو فضای نرمدار $$X$$ و $$Y$$ «به طور متقارن همریخت» (Isometrically Isomorphic) هستند، اگر علاوه بر همریختی، متقارن هم باشند. این امر به این معنی است که برای هر $$x$$ در $$X$$ داشته باشیم:
$$ \large ||T(x)|| = ||x|| , \forall x \in X $$
در این بین «فاصله باناخ-مازور» (Banach-Mazur Distance) بین دو فضای همریخت، میزان اختلاف دو فضای $$X$$ و $$Y$$ را نشان میدهد، به شرطی که این دو فضا، متقارن به مفهوم بالا نباشند.
فاصله باناخ-مازور
فرض کنید دو فضای متناهی بُعد نرمدار با ابعاد یکسان $$X$$ و $$Y$$ در اختیارمان است. $$GL(X,Y)$$ را مجموعهای از تمامی روابط خطی همریخت مثل $$T:X \rightarrow Y $$ در نظر بگیرید. اگر $$||T||$$ را عملگر نرم برای چنین نگاشتی باشد آنگاه فاصله باناخ-مازور به شکل زیر بین $$X$$ و $$Y$$ تعریف میشود.
$$ \large \delta(X, Y) = \log \Bigl( \inf \{ \|T\| \|T^{-1}\| : T \in \operatorname{ G L }(X, Y) \} \Bigr) $$
البته واضح است که اگر $$\delta(X,Y) = 0 $$ آنگاه فضای $$X$$ و $$Y$$ به طور متقارن همریخت هستند و برعکس. در ضمن منظور از $$\inf$$ نیز بزرگترین کران پایین یا همان اینفیمم (Infimum) است.
البته بعضی اوقات فاصله باناخ-مازور را به بدون محاسبه لگاریتم و به شکل زیر در نظر میگیرند که به آن فاصله ضربی باناخ-مازور هم گفته میشود.
$$ \large d(X, Y) := \mathrm{e}^{\delta(X, Y)} = \inf \{ \|T\| \|T^{-1}\| : T \in \operatorname{ G L }(X, Y) \}$$
که در این حالت روابط زیر برقرار است. به یاد دارید که این شرطها همواره برای یک تابع فاصله (Distance Function) باید برقرار باشد.
$$ \large d(X, Z) \leq d(X, Y) d(Y, Z) $$
$$ \large d(X, X) = 1 $$
همانطور که میبینید، نامساوی مثلثی که در اولین رابطه دیده میشود، براساس ضرب فاصلهها نوشته شده در حالیکه در تعریف اولیه برای فاصله باناخ-مازور، نامساوی مثلثی برحسب مجموعه فاصلهها خواهد بود.
مثالهایی از فضای باناخ
مشخص است که فضای $$L^p$$ به عنوان یک فضای پایه، یک حالت خاص از فضای باناخ است. برای مثال فضای $$l^1$$ که از یک دنباله از قدر مطلق جمعپذیر تشکیل شده یک فضای باناخ است. در این فضا، فاصله به وسیله مجموع قدرمطلقها شناخته میشود. همچنین فضای $$l^2$$ که دنبالهای از مربعات جمعپذیر است هم تشکیل یک فضای باناخ میدهد. در این فضا، فاصله اقلیدسی یا مربع آن معیار سنجش فاصله خواهد بود.
فضای هیلبرت (Hilbert Space) به عنوان یک مثال از فضای باناخ در نظر گرفته میشود. در فضای هیلبرت $$H$$ که روی فضای برداری حقیقی یا مختلط تشکیل میشود، اندازه یا نرم به صورت ضرب برداری و به شکل زیر معرفی میشود:
$$ \large \|x\|_{H}={\sqrt {\langle x,x\rangle }} $$
در رابطه بالا، عملگر نقطه به شکل $$ \langle \cdot ,\cdot \rangle :H\times H\to \mathbf {K} $$ بوده که در آن $$K = R , C $$ یعنی یا مجموعه اعداد چند بعدی حقیقی یا مختلط است. در نتیجه فضای هیلبرت میتواند برای بردارهای حقیقیمقدار یا با مقادیر مختلط تعریف شود.
فضای ضرب داخلی دارای خواص زیر است. از طرفی ضرب داخلی نسبت به مولفه اولش، خطی است.
$$ \large { \begin{aligned} \forall x,y \in H:\quad \langle y,x\rangle & = { \overline { \langle x,y \rangle }},\\ \large \forall x \in H: \quad \langle x,x \rangle & \geq 0,\\ \large \langle x,x \rangle = 0 \Leftrightarrow x & = 0 .\end{aligned}} $$
برای مثال میتوان گفت که فضای $$L^2$$ یک فضای هیلبرت است.
فضای دوگان
یک فضای نرمدار مثل $$X$$ تحت میدان $$K$$ (که ممکن است اعداد حقیقی یا اعداد مختلط باشد) را در نظر بگیرد. فضای دوگان پیوسته (Continuous Dual Space)، به فضایی گفته میشود که از نگاشتهای خطی $$X$$ به $$K$$ تشکیل شده که گاهی به آنها تابعکهای خطی پیوسته (Continuous Linear Functionals) نیز میگویند.
نمادی که برای نمایش این فضای دوگان استفاده میشود، مطابق با تعریف ارائه شده به شکل $$X'= B(X,K)$$ است. از آنجایی که $$K$$ یک فضای باناخ با نرم قدرمطلق است، فضای دوگان $$X'$$ نیز یک فضای باناخ برای هر فضای نرمدار $$X$$ خواهد بود.
در این بین برای اثبات وجود تابعکهای خطی پیوسته، باید از فضیه «هان-باناخ» (Hahn-Banach Theorem) استفاده کرد. صورت این قضیه در ادامه بیان شده است.
قضیه هان-باناخ
فضای برداری $$X$$ روی میدان $$K = R, C $$ را در نظر بگیرید. همچنین فرض کنید شرطهای زیر برقرار هستند.
- $$Y$$ که زیرمجموعه $$X$$ است ($$ Y \subseteq X$$)، یک زیرفضای خطی است.
- $$p$$ که از $$X$$ به $$R$$ تعریف شده ($$p: X \rightarrow R$$)، یک تابع زیرخطی (Sublinear Function) است.
- $$f$$ از $$Y$$ به $$K$$ یک تابعک خطی است.
در نتیجه رابطه زیر برقرار است:
$$ \large \forall y \in Y,\; Re(f(y)) \leq p(y) $$
مشخص است که منظور از $$Re$$ قسمت حقیقی مقدار تابع مختلط $$f(y)$$ است.
مثال از فضاهای دوگان
فضای باناخ $$L^p([0,1])$$ را در نظر بگیرید. دوگان این فضا به صورت $$L^q([0,1]$$ است که به شکل متقارن همریخت بوده و در آن رابطه زیر بین $$p$$ و $$q$$ برقرار است.
$$ \large \frac{1}{p} + \frac{1}{q} = 1 , \;\; 1 \leq p < \infty $$
قضیه باناخ
باناخ در کتاب خود به نام «نظریه عملگرهای خطی» (Theory of Linear Operations) که سال ۱۹۳۲ منتشر شد، قضایا و نتایجی را براساس فضای ایجاد شده مطرح کرد. برمبنای این قضیه، فضای متریک کامل (مانند فضای باناخ و فضای F) را نمیتوان برحسب اجتماع شمارشپذیری از زیرمجموعههای بسته ایجاد کرد، مگر آنکه فضای باناخ با یکی از آن مجموعهها برابر باشد. همچنین این فضیهها نشان میدهند که فضای باناخ با پایههای شمارشپذیر، حتما متناهی-بُعد خواهد بود.
قضیه باناخ-اشتنهاوس
فرض کنید $$X$$ یک فضای باناخ و $$Y$$ نیز یک فضای برداری نُرمدار باشد. همچنین $$F$$ را یک مجموعه از ترکیبات خطی از $$X$$ به $$Y$$در نظر بگیرید. «اصل کرانداری یکنواخت» (Uniform Boundedness Principle) بیان میکند که اگر برای همه $$x$$های درون $$X$$، نرم $$T(x)$$ دارای کوچکترین کران بالا متناهی باشد، آنگاه نرم $$T$$ هم روی همه مقادیر، دارای کوچکترین کران بالای متناهی (Supremum) است. به بیان ریاضی این عبارت به صورت زیر نوشته خواهد شد.
$$ \large \forall x \in X , \sup_{ T \in F }||T(X)||_Y < \infty \rightarrow \sup_{ T \in F }||T||_Y < \infty $$
یاددآوری این نکته نیز ضروری است که این فضیه فقط به فضای باناخ محدود نمیشود. برای مثال این فضیه برای «فضای فرشه» (Frechet Space) نیز برقرار است و به شکل زیر نوشته خواهد شد.
یک همسایگی مانند $$U$$ حول نقطه مبدا در فضای $$X$$ وجود دارد که باعث میشود، همه $$T$$هایی که در $$F$$ هستند به طور یکنواخت کراندار روی $$U$$ باشند.
$$ \large \sup _{T\in F}\sup _{x\in U}\;\|T(x)\|_{Y}<\infty . $$
قضیه نگاشت باز
در «قضیه نگاشت باز» (Open Mapping Theorem) دو فضای باناخ و تبدیل یا نگاشت بین آنها مورد بررسی قرار میگیرد. باز هم $$X$$ و $$Y$$ را فضاهای باناخ در نظر بگیرید و $$T$$ را هم یک نگاشت (Map) از $$X$$ به $$Y$$ که پیوسته و یک عملگر خطی دو طرفه است، تصور کنید.
$$ \large T: X \rightarrow Y , \,\,\,\text{ Surjective, Continuous, Linear Operator} $$
آنگاه $$T$$ یک نگاشت باز (Open Map) خواهد بود.
بر این اساس آخرین قضیه (نگاشت باز)، میتوان گفت که هر نگاشت با عملگر خطی کراندار و یک به یک از یک فضای باناخ به فضای باناخ دیگر حتما همریختی (Isomorphism) ایجاد میکند.
خلاصه و جمعبندی
در این نوشتار با تعریف فضای باناخ و خصوصیات آن آشنا شدید. همچنین ویژگیهای این فضا و مقایسه آن با فضای هیلبرت و فضای اقلیدسی مورد بحث قرار گرفت. به این ترتیب مشخص است که فضای باناخ با توجه به تعریف ارائه شده نقش مهمی در آنالیز تابعی و مباحث مربوطه دارد.










