انتگرال دوگانه روی سطوح عمومی — از صفر تا صد (+ دانلود فیلم آموزش رایگان)

در مطالب گذشته ریاضی وبلاگ فرادرس، در مورد محاسبه انتگرال دوگانه و مفاهیم آن صحبت کردیم. از این رو در این مطلب قصد داریم تا در قالب مثال‌هایی نحوه محاسبه انتگرال دوگانه روی سطوح عمومی را توضیح دهیم. البته به منظور درک بهتر پیشنهاد می‌شود در ابتدا مطلب انتگرال دوگانه را مطالعه فرمایید.

انتگرال دوگانه روی سطوح

همانطور که در مبحث انتگرال دوگانه نیز توضیح داده شد، انتگرال تابعی دو متغیره روی سطح $$D$$، مطابق با رابطه زیر بدست می‌آید.

$$\large \iint \limits _ { D } { { f \left ( { x , y } \right ) \, d A } }$$

فیلم آموزش ریاضی عمومی 2 – جامع و کاربردی در فرادرس

کلیک کنید

در حالت کلی دو نوع ناحیه به منظور محاسبه انتگرال دوگانه وجود دارد. این نواحی با توجه به افقی یا عمودی بودنشان دسته‌بندی می‌شوند. در شکل زیر این دو ناحیه نشان داده شده‌اند.

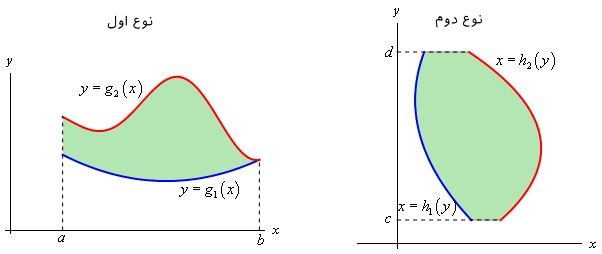
تعریف ریاضیاتی ناحیه نوع اول به صورت زیر است.

$$\large D = \left \{ { \left ( { x , y } \right ) |a \le x \le b,\,\, { g _ 1 } \left ( x \right ) \le y \le { g _ 2 } \left( x \right ) } \right \}$$

در ادامه نیز تعریف ناحیه دوم ارائه شده‌ است.

$$\large D = \left \{ { \left ( { x , y } \right ) |{ h _ 1 } \left ( y \right ) \le x \le { h _2 } \left ( y \right ) ,\,c \le y \le d } \right \}$$

انتگرال دوگانه برای هر دو حالت فوق، به صورت انتگرال‌هایی مکرر بیان می‌شوند.

به منظور محاسبه انتگرال در ناحیه نوع اول در ابتدا نسبت به $$y$$، سپس نسبت به $$x$$ انتگرال گرفته می‌شود. بنابراین ناحیه $$D$$ به صورتِ $$D = \left \{ { \left ( { x , y } \right ) |a \le x \le b,{ g _ 1 } \left ( x \right ) \le y \le { g _ 2 } \left ( x \right ) } \right \}$$ بیان می‌شود؛ در نتیجه در ابتدا انتگرال نسبت به $$y$$ و سپس نسبت به $$x$$ گرفته می‌شود. در این حالت حاصل انتگرال دوگانه برابر است با:

$$\large \iint \limits _ { D } { { f \left ( { x , y } \right ) \, d A } } = \int _ { { \, a } } ^ { { \, b } } { { \int _ { { { g _ { \,1 } } \left ( x \right ) } } ^ { { { g_ { \, 2 } } \left ( x \right ) } } { { f \left ( { x , y } \right ) \, d y } } \, d x } }$$

به همین صورت در حالت دوم نیز $$D$$ به صورت $$D = \left \{ { \left ( { x , y } \right) | { h _ 1 } \left( y \right) \le x \le { h _ 2 } \left ( y \right ) ,\,c \le y \le d} \right \}$$ بیان می‌شود؛ بنابراین حاصل انتگرال دوگانه نیز در این حالت به صورت زیر بدست می‌آید.

$$ \large \iint\limits _ { D } { { f \left ( { x , y } \right ) \, d A } } = \int _ { { \, c } }^ { { \, d } } { { \int _ { { h { \, _ 1 } \left ( y \right ) } } ^ { { { h _ { \, 2 } } \left( y \right ) } } { { f \left ( { x , y } \right ) \, d x } } \, d y } } $$

قبل از ارائه مثال‌ها، باید با برخی از ویژگی‌های انتگرال دوگانه آشنا باشید. توجه داشته باشید که تمامی ویژگی‌های ارائه شده، در حقیقت ویژگی‌های انتگرال عادی هستند که توسعه یافته‌اند.

ویژگی‌های انتگرال دوگانه

۱. برای هر ناحیه‌ای از $$D$$ می‌توان گفت:

$$\large \displaystyle \iint \limits _ { D } { { f \left ( { x , y } \right ) + g \left ( { x , y } \right ) \, d A } } = \iint \limits _ { D } { { f \left ( { x , y } \right)\, d A } } + \iint \limits _ { D } { { g \left ( { x , y } \right ) \, d A } }$$

فیلم آموزش ریاضی عمومی ۲ – مرور و حل تمرین در فرادرس

کلیک کنید

۲. با فرض این‌که $$c$$ عددی ثابت باشد، می‌توان رابطه زیر را بیان کرد:

$$\large \displaystyle \iint \limits _ { D } { { c f \left ( { x , y } \right ) \, d A } } = c \iint \limits _ { D } { { f \left ( { x , y } \right)\, d A } }$$

۳. هم‌چنین اگر ناحیه‌ $$D$$ را بتوان به دو قسمت تقسیم کرد، در این صورت می‌توان حاصل جمع انتگرال روی هریک از نواحی را به صورت زیر بیان کرد:

$$\large \iint \limits _ { D } { { f \left ( { x , y } \right ) \, d A } } = \iint \limits _  { { { D _ 1 } } } { { f \left ( { x , y } \right ) \, d A } } + \iint \limits _ { { { D _ 2 } } } { { f \left ( { x , y } \right ) \, d A } }$$

ویژگی‌های فوق کاملا بدیهی به نظر می‌رسند، اما این ویژگی‌ها در حل مسائل انتگرال دوگانه نیز بسیار پرکاربرد هستند.

مثال ۱

حاصل هریک از انتگرال‌‌های زیر را روی ناحیه $$D$$ بیابید.

1. $$\large \displaystyle \iint \limits _ { D } { { { { \bf { e } } ^ { \frac { x }{ y } } } \, d A } } \ , \ D = \left\{ {\left( {x,y} \right)|1 \le y \le 2,\,\,y \le x \le {y^3}} \right\}$$
2. $$\large \displaystyle \iint \limits _ { D } { { 4 x y - { y ^ 3 } \, d A } }$$ و $$D$$ ناحیه محدود به دو نمودار $$y = \sqrt x$$ و $$y = x ^ 3$$ است.
3. $$\displaystyle \iint \limits _ { D } { { 6 { x ^ 2 } - 40 y \, d A } }$$ و $$D$$ مثلثی با رئوس $$\left( {0,3} \right )$$ و $$\left ( { 1 , 1 } \right )$$ و $$\left ( { 5 , 3 } \right )$$ است.

(a): حاصل این انتگرال برابر است با:

$$\large \begin {align*} \iint \limits _ { D } { { { { \bf { e } } ^ { \frac { x }{ y } } } \, d A } } & = \int _ { { \, 1 } } ^ { { \, 2 } } { { \int _ { { \, y } } ^ { { { y ^ 3 } } } { {‌ { {\bf { e } } ^ { \frac { x } {y } } } \, d x } } \, d y } } = \int _ { { \, 1 } } ^ { { \, 2 } } { { \left. { y \, { { \bf { e } } ^ { \frac { x } { y } } } } \right| _ y ^ { { y ^ 3 } } \, d y } } \\ & = \int _ { { \, 1 } } ^ { { \, 2 } } { { y \, { { \bf { e } } ^{ { y ^ 2 } } } - y { { \bf { e} } ^ 1 } \, d y } } \\ & = \left. { \left ( { \frac { 1 } { 2 } { { \bf { e } } ^ { { y ^ 2 } } } - \frac { 1 } { 2 } { y ^ 2 } { { \bf { e } } ^ 1 } } \right ) } \right| _ 1 ^ 2 = \frac { 1 } { 2 } { { \bf { e } } ^ 4 } - 2 { { \bf { e } } ^ 1 } \end {align*}$$

(b): در این انتگرال، ناحیه $$D$$، محدود شده بین دو نمودار $$y = \sqrt x$$ و $$y = { x ^ 3 }$$ است.

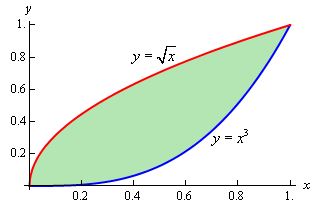
با توجه به نمودار فوق می‌توان دید که ناحیه انتگرال‌گیری در بازه زیر قرار دارد.

$$\large 0 \le x \le 1 \hspace {0.25in} , \hspace {0.25in} { x ^ 3 } \le y \le \sqrt x$$

در نتیجه حاصل انتگرال دوگانه نیز برابر است با:

$$\large \begin{align*}\iint\limits _ { D } { { 4 x y - {y^3}\,dA}} & = \int _ { { \, 0 } } ^ { { \, 1 } } { { \int _ { { \, { x ^ 3 } } } ^ { { \,\sqrt x } } { { 4 x y - { y ^ 3 } \, d y } } \, d x } } \\ & = \int _ { { \, 0 } } ^ { { \, 1 } } { { \left. { \left ( { 2 x { y ^ 2 } - \frac { 1 } { 4 } { y ^ 4 } } \right ) } \right| _ { { x ^ 3 } } ^ { \sqrt x } \, d x } } \\ & = \int _ { { \, 0 } } ^ { { \, 1 } } { { \frac { 7 } { 4 } {x ^ 2 } - 2 { x ^ 7 } + \frac { 1 }{ 4 } { x ^ { 12 } } \, d x } } \\ & = \left. { \left ( {\frac { 7 } { { 1 2 } } { x ^ 3 } - \frac { 1 } { 4 } { x ^ 8 } + \frac { 1 } { { 52 } } { x ^ { 1 3 } } } \right ) } \right|_ 0 ^ 1 = \frac { { 5 5} } { { 1 5 6} } \end{align*}$$

(c): با توجه به نقاط بیان شده، ناحیه انتگرال‌گیری به صورت زیر است.

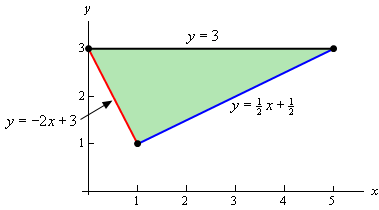
مرز‌های مثلث را می‌توان با استفاده از معادله خط بدست آورد. ناحیه فوق را می‌توان به دو بخش تقسیم کرد. یکی از نقطه‌ها در موقعیت $${ ( 1 , 0 ) }$$ و نقطه دوم نیز در موقعیت $${ ( 5 , 1 ) }$$ قرار دارد. بنابراین نواحی $$D _ 1$$ و $$D _ 2$$ را می‌توان به صورت زیر بیان کرد:

$$\large \begin {align*} { D _ 1 } & = \left \{ { \left ( { x , y } \right ) |0 \le x \le 1,\,\,\, - 2 x + 3 \le y \le 3 } \right \} \\ { D _ 2 } & = \left \{ { \left ( { x , y } \right ) |1 \le x \le 5,\,\,\,\frac { 1 } { 2 } x + \frac { 1 } { 2 } \le y \le 3} \right \} \end {align*}$$

حال می‌توان ناحیه نهایی به منظور انتگرال‌گیری را به صورت زیر در نظر گرفت.

$$\large D = { D  _ 1 } \cup { D _2 }$$

اگر بخواهیم انتگرال‌گیری را در راستای محور $$x$$ انجام دهیم، بازه‌های انتگرال‌گیری باید بر حسب $$x$$ بیان شوند. لذا بازه‌های انتگرال‌گیری برابرند با:

$$\large \begin{align*}y & = - 2x + 3 \hspace {0.5in} \Rightarrow \hspace {0.5in} x = - \frac { 1 } { 2 } y + \frac { 3 } { 2 } \\ y & = \frac { 1 } { 2 } x + \frac { 1 } { 2 } \hspace{0.5in} \Rightarrow \hspace{0.5in}x = 2 y - 1 \end {align*}$$

مجموع دو بازه فوق را می‌توان به صورت زیر بیان کرد:

$$\large D = \left \{ { \left ( { x ,y } \right )|\,\, - \frac { 1 } { 2 } y + \frac { 3 } { 2 } \le x \le 2 y - 1,\,\,\,1 \le y \le 3} \right \}$$

بازه فوق زمانی کاربرد دارد که به منظور انتگرال‌گیری در جهت $$y$$ حرکت کنیم. هر دو روش فوق (مجموع دو ناحیه یا ناحیه یکپارچه) باید پاسخی یکسان را به ما بدهند. از این رو در ادامه حاصل انتگرال را به هر دو روش بدست می‌آوریم.

روش اول

در این روش، هریک از نواحی به صورت جداگانه انتگرال‌گیری شده، سپس با هم جمع می‌شوند. هم‌چنین در این حالت، در ابتدا نسبت به $$x$$ از تابع انتگرال‌گیری می‌شود.

$$\begin{align*} \iint \limits _ {D } { { 6 { x ^ 2 } - 40 y \, d A } } & = \iint \limits _ { { {D_ 1 } }} { { 6 {x ^ 2 } - 40 y \, d A } } + \iint \limits _ { {{ D _ 2 } } } { { 6 { x ^ 2 } - 40 y \, d A } } \\ & = \int _ { { \, 0 } } ^ {{ \, 1 } }{ { \int _ { { \, - 2 x + 3 } } ^ { { \, 3 } } { { 6 { x ^ 2 } - 40 y \, d y } } \, d x } } + \int _ { { \, 1 } } ^ { { \, 5 } } { { \int_{{\,\frac{1}{2}x + \frac{1}{2}}}^{{\,3 } } { {6 { x ^ 2 } - 40y\, d y } } \, d x } } \\ & = \int_{{\,0}}^{{\,1}}{{\left. {\left( { 6 { x ^ 2 } y - 20 { y ^ 2 } } \right ) } \right| _ { - 2x + 3}^3\,dx}} + \int_{{\,1}}^{{\,5}}{{\left. {\left( { 6 { x ^ 2 } y - 20{y^2}} \right)} \right|_{\frac{1}{2}x + \frac{ 1 } { 2} } ^ 3\,dx}}\\ & = \int _ { { \, 0 }} ^ { { \, 1 } }{ { 12 { x^ 3 } - 180 + 20{{\left( {3 - 2x} \right ) } ^ 2 } \, d x } } + \int_{{\,1}}^{{\,5 } } { { - 3 { x ^ 3 } + 15{x^2} - 180 + 20 { { \left( {\frac{1}{2}x + \frac{1} { 2 } } \right)} ^ 2 } \, d x } } \\ & = \left. {\left( {3{x^4} - 180x - \frac {{ 10 }} { 3 }{ {\left ( { 3 - 2 x } \right ) } ^ 3 } } \right)} \right|_0^1 + \left. {\left( { - \frac { 3 } {4 } { x ^4 } + 5 { x ^ 3 } - 180 x + \frac{{40 } } {3} { { \left( {\frac{1} { 2 } x + \frac { 1 } { 2 } } \right ) } ^ 3 } } \right)} \right|_1^5\\ & = - \frac { { 935 } } { 3 } \end{align*}$$

فیلم آموزش ریاضی عمومی ۲ + حل مثال در فرادرس

کلیک کنید

روش دوم

این روش به دلیل یکپارچه فرض شدن ناحیه انتگرال‌گیری، زمان کوتاه‌تری را به منظور پاسخ به سوال نیاز خواهد داشت. هم‌چنین در این حالت انتگرال‌گیری در ابتدا نسبت به $$x$$ انجام می‌شود. حاصل انتگرال برابر است با:

$$\begin {align*}\iint \limits _ { D } { {6 { x ^ 2 } - 40 y \, d A } } &= \int _ { 1} ^ { 3 } { { \int _ { { - \frac { 1 } { 2 } y + \frac { 3 } {2 } } }^ { {2 y - 1 } }{{6{x^2} - 40y\,d x } } \, d y } } \\ & = \int_{1}^{3}{{\left. {\left( { 2 { x ^ 3 } - 40xy} \right)} \right|_{ - \frac{1}{2}y + \frac{3}{2}}^{2y - 1}\,dy}}\\ & = \int _ { 1} ^ { 3} { { 100 y - 100 { y ^ 2 } + 2{{\left( {2y - 1} \right)}^3} - 2{{\left( { - \frac{1}{2}y + \frac{3}{ 2 } } \right)}^3}\,dy}}\\ & = \left. {\left( {50{y^2} - \frac{{100 } } {3 } { y^ 3 } + \frac{1}{4}{{\left( {2y - 1} \right ) } ^ 4 } + {{\left( { - \frac{1}{2}y + \frac{3}{ 2 } } \right)}^4}} \right)} \right| _ 1 ^ 3 \\ & = - \frac { { 935 } }{ 3 } \end{align*}$$

همان‌طور که مشاهده می‌کنید، هر دو حالت پاسخی یکسان را به ما می‌دهند. همان‌طور که در مثال فوق نشان داده شد انتگرال‌های دوگانه را می‌توان با استفاده از دو روش محاسبه کرد. در حقیقت ترتیب متغیر‌ها در انتگرال‌گیری، تعیین‌کننده نوع انتگرال است.

در ادامه چند مثال دیگر از نحوه محاسبه انتگرال دوگانه و کاربرد آن در مسائل هندسی ارائه شده که مطالعه آن‌ها را به شما پیشنهاد می‌کنیم.

مثال ۲

حجم ناحیه جامد قرار گرفته زیر رویه $$z = 16 x y + 200$$ و بخشی از صفحه $$x y$$ که توسط دو منحنی $$y = { x ^ 2 }$$ و $$y = 8 - { x ^ 2 }$$ محدود شده را بیابید.

در شکل زیر ناحیه مد نظر نشان داده شده است.

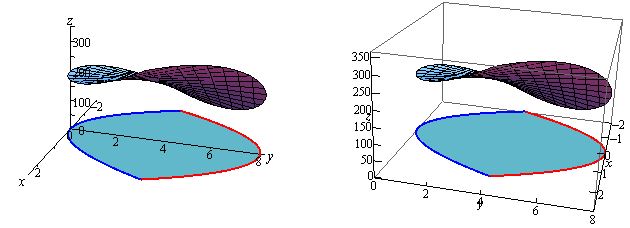
ناحیه قرار گرفته روی صفحه $$x y$$ به صورت زیر است.

با برابر قرار دادن دو منحنی نقاط $$x = 2$$ و $$x = - 2$$ به عنوان نقاط برخورد دو منحنی بدست می‌آیند. در نتیجه بازه انتگرال به صورت زیر است.

$$\large \begin {array} { c } - 2 \le x \le 2 \\ { x ^ 2 } \le y \le 8 - { x ^ 2 } \end {array}$$

به منظور بدست آوردن حجم کافی است رویه قرار گرفته در بالای صفحه $$x y$$ را به عنوان تابع انتگرال‌گیری در نظر گرفته و حاصل انتگرال را بدست آوریم:

$$\large \begin{align*}V &= \iint\limits _ { D } { { 16 x y + 200 \, d A } } \\ & = \int _ { { - 2 } } ^ { { \, 2 } } { { \int _ { {{ x ^ 2 } } } ^ { { 8 - { x ^ 2} } } { { 1 6 x y + 200\, d y } } \, d x } } \\ & = \int_{{ - 2 } } ^ { { \,2 } } { { \left. {\left ( {8x{y^2} + 200 y } \right ) } \right| _ { { x ^ 2 }} ^ { 8 - { x ^ 2 } } \, d x } } \\ & = \int_{{ - 2 } } ^ { { \,2 } } { { - 128 { x ^ 3 } - 400 { x ^ 2 } + 512x + 1600 \, d x } } \\ & = \left. {\left ( { - 32{x^4} - \frac { { 400 } } { 3 } { x ^ 3} + 256 { x ^ 2 } + 1600 x } \right ) } \right|_{ - 2 } ^ 2 = \frac { { 12800 } } { 3 } \end{align*}$$

مثال ۳

حجم محدود به سطوح $$4 x + 2 y + z = 10 \ , \ y = 3 x \ , \ z = 0 , x = 0$$ را بیابید.

فیلم آموزش ریاضی مهندسی – مرور و حل سوالات کنکور دکتری در فرادرس

کلیک کنید

این مسئله نسبت به مسئله قبل اندکی متفاوت‌تر است. چرا که در آن مشخصا ناحیه انتگرال‌گیری به صورت صریح ارائه نشده است. با توجه به مفاهیم بیان شده در مطلب معادله صفحه می‌توان گفت هدف محاسبه حجم قرار گرفته تحت صفحه زیر است.

$$\large z = 10 - 4 x - 2 y$$

در شکل زیر این ناحیه به همراه صفحات مجانبی آن نشان داده شده‌اند.

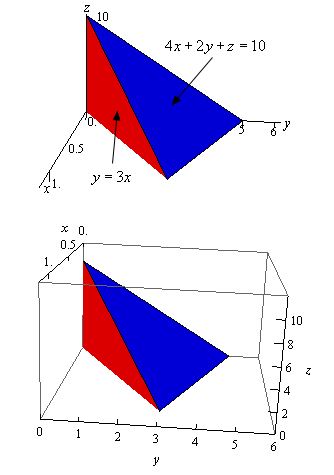
توجه داشته باشید که ناحیه $$D$$، فضای محدود شده بین $$y = 3 x$$ و $$x = 0$$ و تقاطع صفحه $$z + 4 x + 2 y = 10$$ با صفحه $$x y$$ است. این تقاطع با قرار دادن $$z = 0$$ در معادله $$z$$ بدست می‌آید. با انجام این کار داریم:

$$\large 0 + 4 x + 2 y = 10 \hspace {0.1in} \Rightarrow \hspace {0.1in} 2 x + y = 5 \hspace {0.1in} \Rightarrow \hspace {0.1in} y = - 2 x + 5$$

بنابراین ناحیه $$D$$ قرار گرفته روی $$x y$$ به صورت زیر است.

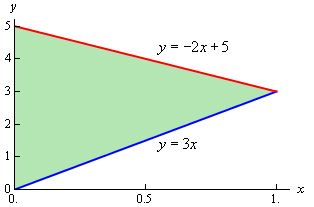
با توجه به نمودار فوق، می‌توان نامساوی زیر را به منظور توصیف ناحیه $$D$$ برای آن نوشت.

$$\large \begin {array} { c } 0 \le x \le 1 \\ 3 x \le y \le - 2 x + 5 \end {array}$$

در نتیجه اندازه حجم قرار گرفته در زیر این رویه برابر است با:

$$\large \begin {align*} V & = \iint \limits _ { D } { { 1 0 - 4 x - 2 y \, d A } } \\ & = \int _ {0  } ^ { { \, 1 } } { { \int _  { { 3 x } } ^ { { - 2 x + 5 } } { { 10 - 4 x - 2 y \, d y } } \, d x } } \\ & = \int _ { 0 } ^ { { \, 1 } } { { \left. { \left ( { 10 y - 4 x y - { y ^ 2 } } \right ) } \right| _  { 3 x } ^ { - 2 x + 5 } \, d x } } \\ & = \int _ { 0 } ^ { { \, 1 } }{ { 2 5 { x ^ 2 } - 50 x + 25 \, d x } } \\ & = \left. {\left( {\frac { {2 5 } } {3 } { x ^ 3 } - 25 { x ^ 2 } + 2 5 x } \right ) } \right| _ 0 ^ 1 = \frac{ { 2 5 }} { 3} \end {align*}$$

احتمالا شما نیز از مثال فوق متوجه شده‌اید که حجم محصور شده به رویه $$z = f \left ( { x , y } \right )$$ برابر است با:

$$\large V = \iint \limits _ { D } { { f \left ( { x , y } \right ) \, d A } }$$

از شکل انتگرال نیز می‌توان دریافت که $$D$$ نشان‌دهنده ناحیه قرار گرفته روی صفحه $$x y$$ است. در چنین مواردی بخش‌های بالای صفحه، مثبت و بخش‌های پایین آن منفی هستند. دقیقا روشی مشابه به منظور محاسبه مساحت در انتگرال عادی استفاده می‌شود. در این روش مساحت تحت نمودار برابر است با:

$$\large V = \iint \limits _ { D } { { f \left ( { x , y } \right ) \, d A } }$$

البته مساحت فوق را می‌توان با استفاده از انتگرال دوگانه نیز بدست آورد.

$$ \large {\mbox{Area of } } D = \iint \limits _ { D } { { d A } } $$

به منظور اثبات رابطه فوق، شکل زیر را در نظر بگیرید.

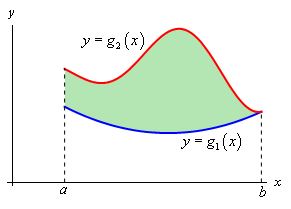
بدیهی است که مساحت فوق برابر است با:

$$\large A = \int _ { { \, a } } ^ { { \, b } } { { { g _ 2 } \left ( x \right ) - { g _ 1 } \left ( x \right ) \, d x } }$$

از طرفی عبارت فوق به صورت زیر به انتگرال دوگانه مرتبط می‌شود.

$$ \large \begin {align*} { \mbox {Area of } } D & = \iint \limits _ { D }{ { d A } } \\ & = \int _ { { \,a } } ^ { { \,b } } { {\int _ { { \, { g _ 1 } \left( x \right)}}^{{\,{g_2}\left( x \right ) } } { { d y } } \,d x } } \\ & = \int _ { { \, a } } ^ { { \, b } } {{\left. y \right| _ { { g _1 } \left ( x \right ) } ^ { { g _ 2 } \left( x \right)}\,d x } } = \int_{{\,a } } ^ { { \, b } } { { { g _ 2 } \left ( x \right ) - {g_1}\left( x \right)\, d x } } \end {align*} $$

بنابراین مساحت یک نمودار دوبعدی را می‌توان با استفاده از انتگرال عادی یا دوگانه به دست آورد.

مثال ۴

حاصل انتگرال دوگانه زیر را روی ناحیه نشان‌ داده شده، بدست آورید.

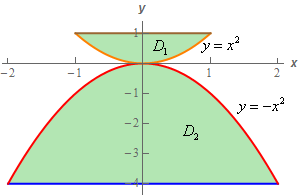
بدیهی است که با استفاده از یک رابطه، نمی‌توان به طور مستقیم انتگرال را بدست آورد. از این رو بهتر است، ناحیه انتگرال‌گیری را مطابق با شکل فوق به دو بخش $$D _ 1$$ و $$D _ 2$$ تقسیم‌بندی می‌کنیم. در نتیجه انتگرال مد نظر را می‌توان به صورت زیر بیان کرد:

$$\large \begin {align*} \iint \limits _ { D } { { 3 - 6 x y \, d A } } & = \iint \limits _ { { {D _ { \, 1 } } } } { { 3 - 6 x y \, d A } } + \iint \limits _ { { { D _ { \, 2 } } } } { { 3 - 6 x y \, d A } } \end {align*}$$

در حقیقت نواحی $$D$$ را می‌توان در قالب ریاضیات به صورت زیر بیان کرد:

$$ \large \begin {array} {*{20}{ c } } \begin{array} { c } { D _ { \,1 } } \,\\ - 1 \le x \le 1\\ { x ^ 2 } \le y \le 1 \end{array} & {\hspace{0.5in}} & \begin {array}{c}{D_{\,2}}\\ - 2 \le x \le 2 \\ - 4 \le y \le - { x ^ 2 } \end {array} \end{array}$$

بنابراین انتگرال را می‌توان به صورت زیر بیان کرد:

$$\large \iint\limits _ { D} { { 3 - 6x y \, d A } } = \int_{{ - 1 } } ^ { 1 } { { \int _ { { { x ^ 2 } } } ^ { 1 } { { 3 - 6 x y \, d y } } \, d x } } + \int _ { { - 2 } } ^ { 2 } { { \int _ { { - 4 } } ^ { { - { x ^ 2 } } } { { 3 - 6 x y \, d y } } \, d x } }$$

حال می‌توان تنها با انتگرال‌گیری ساده‌ای حاصل انتگرال را یافت. در نتیجه با محاسبه انتگرال داریم:

$$\large \begin{align*} \iint \limits _ { D } { { 3 - 6 x y \, d A } } & = \int _ { { - 1 } } ^ { 1 } { { \left. { \left ( { 3 y - 3 x { y ^ 2 } } \right ) } \right| _ { { x ^2 } } ^ 1 \, d x } } + \int _ { { - 2 } } ^ { 2 } { { \left. { \left ( { 3 y - 3 x { y ^2}} \right)} \right|_{ - 4}^{ - { x ^ 2 } } \, d x } } \\ & = \int _ { { - 1 } } ^ { 1 } { { 3{ x ^ 5 } - 3 { x ^ 2 } - 3 x + 3 \, d x } } + \int _ { { - 2 } } ^ {2 } { { 12 + 48x - 3{x^2} - 3 { x ^ 5 } \, d x } } \end {align*}$$

حاصل انتگرال یگانه فوق نیز برابر است با:

$$\large \begin{align*}\iint\limits _ { D }{ { 3 - 6 x y \, d A } } & = \int _ { { - 1 } } ^ { 1 } { { 3 { x ^ 5 } - 3 { x ^ 2 } - 3 x + 3 \, d x } } + \int _ { { - 2 } } ^ { 2 } { { 12 + 48 x - 3 { x ^ 2 } - 3 { x ^ 5 } \, d x } } \\ & = \left. { \left ( {\frac { 1 } { 2 } { x ^ 6 } - {x ^ 3 } - \frac { 3 } {2 } { x ^ 2 } + 3x\,d x } \right)} \right|_{ - 1}^1 + \left. {\left ( {12 x + 24{x^2} - { x ^ 3 } - \frac { 1 }{ 2 } { x ^ 6 } \, d x } \right)} \right| _ { - 2 } ^ 2 \\ & = \hspace {1.15in} 4 \hspace{1.4in} + \hspace {1.15in} 32 \\ & ={ { 36 } } \end {align*}$$

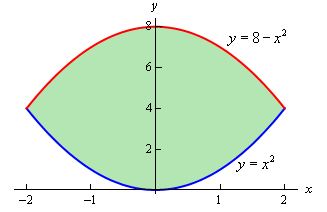
مثال ۵

حاصل انتگرال $$\displaystyle \iint \limits _ { D } { { x \left ( { y - 1 } \right ) \, d A } }$$ را روی ناحیه $$D$$ بیابید. فرض کنید این ناحیه، محدود شده بین دو نمودار $$y = 1 - { x ^ 2 }$$ و $$y = { x ^ 2 } - 3$$ باشد.

دو نمودار بیان شده و ناحیه بین آن‌ها به صورت زیر است.

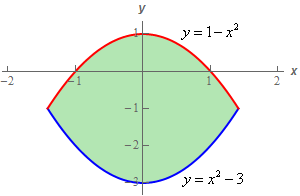
با توجه به شکل فوق می‌توان دید که بازه انتگرال‌گیری باید به صورت زیر باشد.

$$\large \begin {array} { c } - \sqrt 2 \le x \le \sqrt 2 \\ { x ^ 2 } - 3 \le y \le 1 - { x ^ 2 } \end {array}$$

بدیهی است که $$y$$ به صورت متغیر نسبت به $$x$$ در نظر گرفته شده، بنابراین در ابتدا باید از $$y$$ انتگرال‌گیری کرد. در نتیجه حاصل انتگرال مطابق با عبارت زیر بدست می‌آید.

$$\large \begin {align*}\iint \limits _ { D } { { x \left ( { y - 1 } \right ) \, d A } } & = \int _ { { - \sqrt 2 } } ^ { { \sqrt 2 } } { { \int _ { { { x ^ 2 } - 3 } } ^ { { 1 - { x ^ 2 } } } { { x \left( {y - 1} \right ) \, d y } } \, d x } } \\ & = \int_{{ - \sqrt 2 } } ^{ { \sqrt 2 } } { { \left. {\left ( { x \left( {\frac { 1 } { 2 } { y ^ 2 } - y} \right)} \right ) } \right|_{ { x ^ 2 } - 3 } ^ { 1 - { x ^ 2 } } \,d x } } \\ & = \int _ { { - \sqrt 2 } } ^{ { \sqrt 2 } } { { \frac { 1 } { 2 } x { { \left( { 1 - { x ^ 2 } } \right ) } ^ 2 } - \frac { 1 } { 2 } x { { \left( { { x ^ 2 } - 3} \right ) } ^ 2 } - x \left ( { 1 - { x ^ 2 } } \right ) + x \left( { { x ^2 } - 3 } \right ) \, d x } } \end{align*}$$

همان‌طور که مشاهده می‌کنید، ترم‌های قرار گرفته زیر انتگرال همگی فرد هستند. بنابراین با توجه به فرد بودن توابع و متقارن بودن بازه انتگرال‌گیری می‌توان نتیجه گرفت که حاصل انتگرال برابر با صفر است. در نتیجه می‌توان گفت:

$$ \large \begin {align*} \iint \limits _ { D } { { x \left ( { y - 1 } \right ) \, d A } } & = \int _ { { - \sqrt 2 } } ^ { { \sqrt 2 } } { { \frac { 1 } { 2 } x { { \left ( { 1 - { x ^ 2 } } \right ) } ^ 2 } - \frac { 1 } { 2 } x { { \left( { { x ^ 2 } - 3} \right)}^2} + 2 { x ^ 3 } - 4x\, d x } } \\ & = \left. { \left ( { - \frac { 1 } { { 1 2 } } { {\left( {1 - { x ^ 2 } } \right)}^3} - \frac { 1} { { 1 2 } } { { \left ( { { x ^ 2 } - 3} \right ) } ^ 3 } + \frac { 1 } { 2} { x ^ 4 } - 2 { x ^ 2 } } \right)} \right|_{ - \sqrt 2 }^{\sqrt 2 } = \require{bbox} 0 \end{align*}$$

هما‌ن‌طور که مشاهده می‌کنید حاصل انتگرال برابر با صفر بدست می‌آید. البته با توجه به نمودار و تقارن آن نیز می‌توان به همین نتیجه دست یافت. در صورت علاقه‌مندی به مباحث مرتبط در زمینه ریاضی، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های ریاضی
• آموزش ریاضی پایه دانشگاهی
• مجموعه آموزش‌های دروس دانشگاهی
• انتگرال دوگانه — به زبان ساده
• انتگرال — به زبان ساده
• انتگرال و روش‌های محاسبه - به زبان ساده

^^