ارتعاشات اجباری میرا با تحریک هارمونیک – از صفر تا صد

پیش از این در مجله فرادرس و در آخرین مقاله از مجموعه مقالات ارتعاشات مکانیکی، ارتعاشات اجباری را در سیستم‌های نامیرا و با تحریک نیروی هارمونیک بررسی کردیم. در این مقاله، به ارتعاشات اجباری با تحریک هارمونیک در سیستم‌های میرا می‌پردازیم. تحریک هارمونیک می‌تواند ناشی از یک نیروی هارمونیک یا جابجایی هارمونیک باشد که هریک را به صورت جداگانه بررسی و معادلات آن را استخراج خواهیم کرد. ضریب کیفی، قابلیت انتقال جابجایی و قابلیت انتقال نیرو، از دیگر موضوعاتی است که در ادامه به آنها پرداخته می‌شود.

ارتعاشات اجباری با تحریک هارمونیک نیرو

اگر مقاله قبلی مجله فرادرس را در این زمینه خوانده باشید، می‌دانید معادله حرکت برای سیستم جرم، فنر و میراگر تحت ارتعاشات اجباری به صورت زیر نوشته می‌شود.

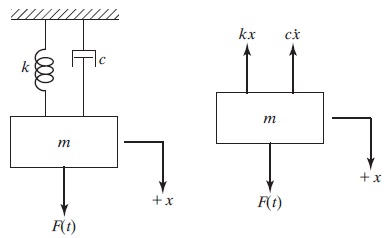
$$\large F(t) \:=\: F_0 \cos \omega t \\~\\
\large m\ddot {x} \:+\: c\dot {x} \:+\: kx \:=\: F_0\cos \omega t$$

(رابطه ۱)

پاسخ خصوصی تحریک هارمونیک بالا را نیز به صورت هارمونیک و به شکل رابطه زیر فرض می‌کنیم.

$$\large x_p(t) \:=\: X \cos (\omega t \:-\: \phi)$$

(رابطه ۲)

در رابطه بالا، $$\large X$$ و $$\large \phi$$ ثابت‌هایی هستند که مقدار آنها باید تعیین شود و به ترتیب، دامنه و زاویه فاز پاسخ را نشان می‌دهند. پاسخ خصوصی را در رابطه ۱، جایگذاری می‌کنیم.

$$\large X\left[ (k\:-\: m\omega ^2) \:\cos (\omega t \:-\: \phi) \:-\: c\omega \:\sin (\omega t \:-\: \phi) \right] \:=\: F_0 \:\cos \omega t$$

(رابطه ۳)

حالا با کمک روابط مثلثاتی زیر، دامنه و فاز را به دست می‌آوریم.

$$\large \cos (\omega t \:-\: \phi) \:=\: \cos \omega t\: \cos \phi \:+\: \sin \omega t\: \sin \phi \\~\\
\large \sin (\omega t \:-\: \phi) \:=\: \sin \omega t\: \cos \phi \:-\: \cos \omega t\: \sin \phi \\~\\
\large X\left[ (k\:-\: m\omega ^2) \cos \phi \:+\: c\omega \: \sin \phi \right] \:=\: F_0 \\~\\
\large X\left[ (k\:-\: m\omega ^2) \sin \phi \:-\: c\omega \: \cos \phi \right] \:=\:0 \\~\\
\large \Rightarrow X \:=\: \frac {F_0} {\left[ (k \:-\: m\omega ^2) ^2 \:+\: c^2 \omega ^2 \right] ^{1/2}}$$

(رابطه 4)

$$\large \phi \:=\: \tan ^{-1} \left( \frac {c \omega} {k \:-\: m \omega ^2} \right)$$

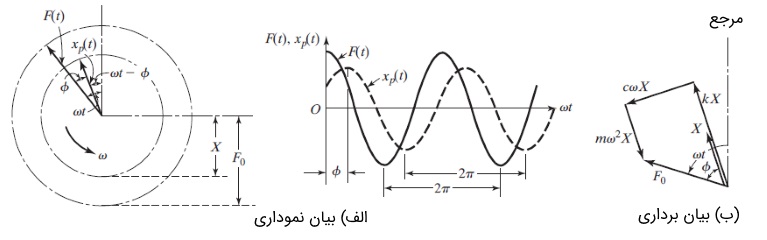
با جایگذاری نتایج بالا در رابطه ۲، پاسخ خصوصی رابطه شماره ۱ به دست می‌آید. شکل زیر، نمودار تابع نیرو و پاسخ حالت ماندگار تحریک هارمونیک را نشان می‌دهد. عبارت‌های مختلف رابطه ۳ را نیز به صورت برداری در قسمت ب مشاهده می‌کنید. با تقسیم صورت و مخرج رابطه ۴ به $$\large k$$ و جایگذاری مقادیر زیر، می‌توانیم رابطه ۵ و ۶ را به ترتیب برای $$\large X/ \delta _{st}$$ و $$\large \phi$$‌ بنویسیم.

$$\large \omega_n \:=\: \sqrt {\frac {k} {m}} \\~\\
\large \zeta \:=\: \frac {c} {c_c} \:=\: \frac {c} {2m \omega _n} \:=\: \frac {c} {2\sqrt {mk}} \\~\\
\large \frac {c} {m} \:=\: 2\zeta \omega_n \\~\\
\large \delta _{st} \:=\: \frac {F_0} {k} \\~\\
\large r \:=\: \frac {\omega} {\omega _n}$$

$$\large \frac {X} {\delta _{st}} \:=\: \frac {1} {\left\{ \left[ 1\:-\: \left( \frac {\omega} {\omega _n} \right) ^2 \right] ^2 \:+\: \left[ 2\zeta \frac {\omega} {\omega _n} \right] ^2 \right\} ^{1/2}} \\~\\
\large \Rightarrow ~~~ \frac {X} {\delta _{st}} \:=\: \frac {1} {\sqrt {\left( 1\:-\: r^2 \right) ^2 \:+\: \left( 2\zeta r \right) ^2}}$$

(رابطه ۵)

$$\large \phi \:=\: \tan ^{-1} \left[ \frac {2\zeta \frac {\omega} {\omega _n}} {1\:-\: \left( \frac {\omega} {\omega _n} \right) ^2} \right] \:=\: \tan ^{-1} \left( \frac {2\zeta r} {1\:-\: r^2} \right)$$

(رابطه ۶)

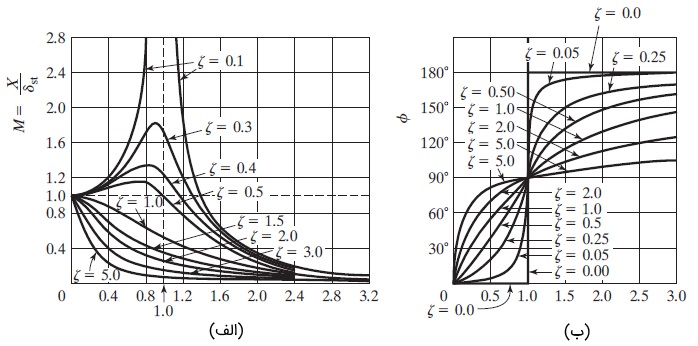
همان‌طور که می‌دانید، عبارت $$\large M\:=\: X/ \delta _{st}$$ ضریب بزرگ‌نمایی یا نسبت دامنه نام دارد. تغییرات $$\large X/ \delta _{st}$$ و $$\large \phi$$‌ برحسب نسبت فرکانس $$\large r$$ و نسبت میرایی $$\large \zeta$$ در شکل زیر رسم شده است. با دقت در رابطه 5 و نمودارهای زیر (قسمت الف)، به نتایجی در مورد ضریب بزرگ‌نمایی در تحریک هارمونیک می‌رسیم.

• در تحریک هارمونیک سیستم نامیرا ($$\large \zeta =0$$)، در حالت $$\large M\rightarrow \infty$$ و $$\large r\rightarrow 1$$، رابطه 5 به رابطه زیر تبدیل می‌شود.

$$\large \frac {X} {\delta _{st}} \:=\: \frac {1} {1 \:-\: \left( \frac {\omega} {\omega _n} \right) ^2}$$

• هر مقداری از میرایی ($$\large \zeta >0$$) مقدار ضریب بزرگ‌نمایی را برای تمام مقادیر فرکانس نیرو، کاهش می‌دهد.
• برای هر نسبت $$\large r$$ مشخص، بیشتر بودن مقدار میرایی، $$\large M$$ را کاهش می‌دهد.
• در حالت رزونانس یا حالتی نزدیک به آن، کاهش $$\large M$$، قابل ملاحظه خواهد بود.
• هرچه فرکانس نیرو بیشتر شود ($$\large r\rightarrow \infty$$)، دامنه ارتعاشات اجباری کوچکتر خواهد شد ($$\large M\rightarrow 0$$).
• در بازه $$\large 0< \zeta <\frac {1} {\sqrt {2}}$$، ماکزیمم مقدار $$\large M$$ هنگامی اتفاق می‌افتد که یکی از روابط زیر برقرار باشد. در این حالت، فرکانس از فرکانس طبیعی نامیرا ($$\large \omega _n$$) و فرکانس طبیعی میرا ($$\large \omega _d= \omega _n \sqrt {1- \zeta ^2}$$) کوچکتر است.

$$\large r\:=\: \sqrt {1\:-\: 2\zeta ^2} \\~\\
\large \omega \:=\: \omega _n \sqrt {1\:-\: 2\zeta ^2}$$

• هنگامی که $$\large r= \sqrt {1- 2\zeta ^2}$$ برقرار باشد، ماکزیمم مقدار $$\large X$$ با کمک رابطه زیر محاسبه می‌شود.

$$\large \left( \frac {X} {\delta _{st}} \right) _{max} \:=\: \frac {1} {2\zeta \sqrt {1\:-\: \zeta ^2}}$$

• همچنین برای به دست آوردن مقدار $$\large X$$ در $$\large \omega= \omega _n$$ نیز از رابطه زیر استفاده می‌کنیم.

$$\large \left( \frac {X} {\delta _{st}} \right) _{\omega \:=\: \omega _n} \:=\: \frac {1} {2\zeta }$$

• در حالتی که $$\large \zeta= \frac {1} {\sqrt {2}}$$ و $$\large r= 0$$ برقرار باشند، تغییرات $$\large M$$ برحسب $$\large r$$ به صورت $$\large \frac {\text {d}M} {\text {d}r} =0$$ است. برای $$\large \zeta> \frac {1} {\sqrt {2}}$$، با افزایش مقادیر $$\large r$$، نمودار $$\large M$$ با شیبی یکنواخت، نزولی خواهد بود.

اکنون به سراغ زاویه فاز می‌رویم. با دقت در رابطه 6 و نمودارهای بالا (قسمت ب)، به نتایجی در مورد ضریب بزرگ‌نمایی می‌رسیم.

• در یک سیستم نامیرا ($$\large \zeta =0$$) رابطه ۶ نشان می‌دهد اگر $$\large 0< r <1$$ باشد، زاویه فاز برابر صفر بوده و اگر $$\large r>1$$ باشد، زاویه فاز برابر با $$\large 180 ^\circ$$ است. از این رو، تحریک و پاسخ در بازه $$\large 0< r <1$$ هم‌فاز هستند و هنگامی که در بازه $$\large r>1$$، رابطه $$\large \zeta =0$$ برقرار باشد، اختلاف فاز دارند.
• در شرایطی که $$\large \zeta >0$$ و $$\large 0< r <1$$ برقرار باشند، زاویه فاز در بازه $$\large 0< \phi <90 ^\circ$$ قرار می‌گیرد و پاسخ نسبت به تحریک، دارای تأخیر است.
• در شرایطی که $$\large \zeta >0$$ و $$\large r>1$$ برقرار باشند، زاویه فاز در بازه $$\large 90 ^\circ< \phi <180 ^\circ$$ قرار می‌گیرد و پاسخ نسبت به تحریک، جلوتر است.
• در شرایطی که $$\large \zeta >0$$ و $$\large r=1$$ برقرار باشند، زاویه فاز برابر با $$\large \phi =90 ^\circ$$ بوده و اختلاف فاز بین تحریک و پاسخ $$\large 90 ^\circ$$ است.
• برای $$\large \zeta >0$$ و مقادیر بزرگ $$\large r$$، زاویه فاز به $$\large 180 ^\circ$$ میل می‌کند و نشان می‌دهد که پاسخ و تحریک، غیر‌هم‌فاز هستند.

پاسخ کلی ارتعاشات اجباری با تحریک هارمونیک

پاسخ کلی ارتعاشات اجباری سیستم میرا با تحریک هارمونیک، با رابطه $$\large x(t) =x_h(t) +x_p(t)$$ بیان می‌شود که در آن، $$\large x_h(t)$$ به صورت زیر تعریف می‌شود.

$$\large x_h(t) \:=\: Xe^ {-\zeta \omega _nt} \cos \left( \sqrt {1\:-\: \zeta^2} \omega _nt \:-\: \phi \right)$$

پاسخ کلی برای سیستم زیر میرایی به صورت زیر است.

$$\large x_(t) \:=\: X_0e^ {-\zeta \omega _nt} \cos \left( \omega_dt \:-\: \phi_0 \right) \:+\: X \cos \left( \omega t \:-\: \phi \right) \\~\\
\large \omega_d \:=\: \sqrt {1\:-\: \zeta ^2} \omega_n$$

مقادیر $$\large X$$ و $$\large \phi$$ با کمک رابطه‌های ۵ و ۶ و مقادیر $$\large X_0$$ و $$\large \phi_0$$ نیز با کمک شرایط اولیه، تعیین می‌شوند. اگر شرایط اولیه را در تحریک هارمونیک به صورت زیر فرض کنیم، مقدار این دو پارامتر به دست خواهد آمد.

$$\large x(t\:=\: 0) \:=\: x_0 \\~\\
\large \dot {x} (t\:=\: 0) \:=\: \dot {x} _0 \\~\\
\large \Rightarrow ~~~ x_0 \:=\: X_0 \cos \phi _0 \:+\: X \cos \phi \\~\\
\large \dot {x} _0 \:=\: -\: \zeta \omega _n X_0 \cos \phi _0 \:+\: \omega _d X_0 \sin \phi _0 \:+\: \omega X \sin \phi$$

(رابطه 8)

به این ترتیب، مقادیر $$\large X_0$$ و $$\large \phi_0$$ قابل محاسبه است.

$$\large X_0 \:=\: \left[ \left( x_0 \:-\: X\cos \phi \right) ^2 \:+\: \frac {1} {\omega ^2_d} \left( \zeta \omega _n x_0 \:+\: \dot{x} _0 \:-\: \zeta \omega _n X \cos \phi \:-\: \omega X \sin \phi \right)^2 \right] ^ {1/2} \\~\\
\large \tan \phi_0 \:=\: \frac {\zeta \omega _n x_0 \:+\: \dot {x} _0 \:-\: \zeta \omega _n X \cos \phi \:-\: \omega X \sin \phi} {\omega _d \left( x_0 \:-\: X \cos \phi \right)}$$

مثال ۱: پاسخ کلی سیستم به تحریک هارمونیک

سؤال: پاسخ کلی یک سیستم یک درجه آزادی با جرم $$\large m= 10kg$$، ضریب میرایی $$\large c= 20\: N.s/m$$ و سفتی $$\large k= 4000\: N/m$$ را با شرایط اولیه $$\large x_0= 0.01m$$ و $$\large \dot {x}_0= 0$$ تحت شرایطی به دست آورید که نیروی خارجی $$\large F(t) =F_0 \cos \omega t$$ با مقادیر $$\large F_0 =100 N$$ و $$\large \omega = 10\: rad /s$$ به سیستم وارد شود.

پاسخ: ابتدا پارامترهای اصلی را می‌یابیم.

$$\large \omega _n \:=\: \sqrt {\frac {k} {m}} \:=\: \sqrt {\frac {4000} {10}} \:=\: 20\: rad/s \\~\\
\large \delta _{st} \:=\: \frac {F_0} {k} \:=\: \frac {100} {4000} \:=\: 0.025 \:m \\~\\
\large \zeta \:=\: \frac {c} {c_c} \:=\: \frac {c} {2\sqrt {km}} \:=\: \frac {20} {2\sqrt {(4000) (10)}} \:=\: 0.05 \\~\\
\large \omega _d \:=\: \sqrt {1\:-\: \zeta ^2} \omega _n \:=\: \sqrt {1\:-\: (0.05) ^2} (20) \:=\: 19.974984 \:rad/s \\~\\
\large r\:=\: \frac {\omega} {\omega_n} \:=\: \frac {10} {20} \:=\: 0.5 \\~\\
\large X\:=\: \frac {\delta _{st}} {\sqrt {(1\:-\: r^2) ^2 \:+\: (2\zeta r) ^2}} \:=\: \frac {0.025} {\left[ (1\:-\: 0.05 ^2) ^2 \:+\: (2 \times 0.5 \times 0.05) ^2 \right] ^ {1/2}} \\~\\
\large \Rightarrow ~~~ X\:=\: 0.03326 \:m \\~\\
\large \phi \:=\: \tan ^{-1} \left( \frac {2 \zeta r} {1\:-\: r^2} \right) \:=\: \tan ^ {-1} \left( \frac {2 \times 0.5 \times 0.05} {1 \:-\: 0.5 ^2} \right) \:=\: 3.814075 ^ \circ$$

حالا از شرایط اولیه و رابطه ۸ استفاده می‌کنیم.

$$\large 0.01 \:=\: X_0 \cos \phi_0 \:+\: (0.03326) (0.997785) \\~\\
\large \Rightarrow ~~~ X_0 \cos \phi _0 \:=\: -\: 0.023186 \\~\\
\large 0\:=\: -\: (0.05) (20) X_0 \cos \phi_0 \:+\: X_0 (19.974984) \:\sin \phi_0 \\~\\
\large +\: (0.03326) (10) \sin (3.814075 ^ \circ) \\~\\
\large \Rightarrow ~~~ X_0 \sin \phi _0 \:=\: -\: 0.002268 \\~\\
\large X_0 \:=\: \left[ \left( X_0 \cos \phi _0 \right) ^2 \:+\: \left( X_0 \sin \phi _0 \right) ^2 \right] ^{1/2} \:=\: 0.023297 \\~\\
\large \tan \phi _0 \:=\: \frac {X_0 \sin \phi_0} {X_0 \cos \phi_0} \:=\: 0.0978176 \\~\\
\large \phi_0 \:=\: 5.586765 ^\circ$$

ضریب کیفی و پهنای باند

اگر میرایی ناچیز باشد ($$\large \zeta < 0.05$$)، می‌توانیم از تقریب زیر استفاده کنیم.

$$\large \left( \frac {X} {\delta _{st}} \right) _{max} \:\cong\: \left( \frac {X} {\delta _{st}} \right) _{\omega \:=\: \omega _n} \:=\: \frac {1} {2\zeta} \:=\: Q$$

مقدار نسبت دامنه در حالت رزونانس یا تشدید، ضریب $$\large Q$$ یا ضریب کیفی سیستم نامیده می‌شود. به نقاط $$\large R_1$$ و $$\large R_2$$ که در آنها ضریب بزرگ‌نمایی برابر با $$\large Q/ \sqrt {2}$$ است نیز نقاط توان نیمه (Half Power Points) گفته می‌شود. زیرا توان جذب شده ($$\large \Delta W$$) توسط میراگر (یا توسط مقاومت در مدار الکتریکی معادل) با مربع دامنه متناسب است. شکل زیر را در نظر بگیرید.

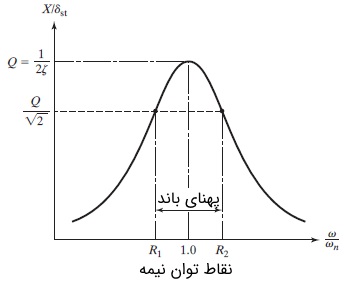
$$\large \Delta W \:=\: \pi c \omega X^2$$

تفاوت بین فرکانس مربوط به نقاط توان نیمه، پهنای باند (Band Width) سیستم نام دارد. برای یافتن مقادیر $$\large R_1$$ و $$\large R_2$$، کافی است در رابطه ۵، مقدار $$\large X/ \delta _{st} = Q/ \sqrt {2}$$ را قرار دهیم.

$$\large \frac {1} {\sqrt {(1\:-\: r^2) ^2 \:+\: (2\zeta r) ^2}} \:=\: \frac {Q} {\sqrt {2}} \:=\: \frac {1} {2\sqrt {2}} \\~\\
\large r^4 \:-\: r^2 (2\:-\: 4\zeta ^2) \:+\: (1\:-\: 8\zeta ^2) \:=\:0$$

ریشه‌های معادله بالا به صورت زیر به دست می‌آید.

$$\large r^2_1 \:=\: 1\:-\: 2\zeta ^2 \:-\: 2\zeta \sqrt {1\:+\: \zeta ^2} \\~\\
\large r^2_1 \:=\: 1\:-\: 2\zeta ^2 \:+\: 2\zeta \sqrt {1\:+\: \zeta ^2}$$

اگر مقدار $$\large \zeta$$ کوچک باشد، جواب‌های بالا به صورت زیر تقریب زده می‌شوند.

$$\large r^2_1 \:=\: R^2_1 \:=\: \left( \frac {\omega_1} {\omega_n} \right) ^2 \:\cong\: 1\:-\: 2\zeta \\~\\
\large r^2_2 \:=\: R^2_2 \:=\: \left( \frac {\omega_2} {\omega_n} \right) ^2 \:\cong\: 1\:+\: 2\zeta$$

در رابطه‌های بالا از تعریف $$\large \omega_1 \:=\: \omega|_ {R_1}$$ و $$\large \omega_2 \:=\: \omega|_ {R_2}$$ استفاده کرده‌ایم. با کمک رابطه بالا، عبارت زیر قابل استخراج است.

$$\large \omega _2^2 \:-\: \omega _1^1 \:=\: (\omega_2 \:+\: \omega_1) (\omega_2 \:-\: \omega_1) \:=\: (R^2_2 \:-\: R^2_1) \omega _n^2 \:\cong\: 4\zeta \omega _n^2$$

با کمک رابطه $$\large \omega _2 \:+\: \omega_1 \:=\: 2\omega _n$$ می‌توانیم پهنای باند را محاسبه کنیم.

$$\large \Delta \omega \:=\: \omega _2 \:-\: \omega _1 \:\cong\: 2\zeta \omega _n$$

ضریب کیفی نیز به صورت زیر به دست می‌آید.

$$\large Q\: \cong\: \frac {1} {2\zeta} \:\cong \:\frac {\omega _n} {\omega_2 \:-\: \omega _1}$$

همان‌طور که مشاهده می‌کنید می‌توان از ضریب کیفی برای تخمین میرایی ویسکوز معادل در یک سیستم مکانیکی بهره برد.

پاسخ سیستم میرا به نیروی مختلط

فرض کنید تابع نیروی تحریک هارمونیک را به شکل مختلط $$\large F(t) = F_0 e^ {i \omega t}$$ معرفی کنیم. در این حالت، معادله حرکت به صورت زیر است.

$$\large m\ddot {x} \:+\: c\dot {x} \:+\: kx \:=\: F_0 e^ {i\omega t}$$

(رابطه ۹)‌

از آنجایی که تحریک واقعی فقط با بخش حقیقی (Real) مربوط به $$\large F(t)$$ انجام می‌شود، پاسخ نیز باید فقط شامل بخش حقیقی $$\large x(t)$$ باشد. زیرا $$\large x(t)$$ نیز یک کمیت مختلط است که در رابطه بالا صدق می‌کند. فرض کنیم، پاسخ خصوصی $$\large x_p(t)$$ به صورت زیر باشد.

$$\large x_p(t) \:=\: Xe^ {i \omega t}$$

دو رابطه اخیر را با هم ادغام می‌کنیم.

$$\large X\:=\: \frac {F_0} { (k \:-\: m\omega ^2) \:+\: ic \omega}$$

(رابطه 10)

صورت و مخرج عبارت سمت راست در رابطه بالا را در $$\large \left[ (k- m \omega^2) -ic \omega \right]$$ ضرب می‌کنیم. با جداسازی بخش‌های حقیقی و موهومی، به رابطه زیر می‌رسیم.

$$\large X\:=\: F_0 \left[ \frac {k \:-\: m\omega ^2} {(k \:-\: m\omega ^2) ^2\: +\: c^2 \omega ^2} \:-\: i \frac {c \omega} {(k \:-\: m\omega ^2) ^2\: +\: c^2 \omega ^2} \right]$$

از رابطه $$\large x+ iy =A e^ {i\phi}$$ استفاده می‌کنیم که در آن $$\large A= \sqrt {x^2 +y^2}$$ و $$\large \phi= y/x$$ برقرار است. حالا می‌توانیم رابطه بالا را به صورت زیر بنویسیم.

$$\large X\:=\: \frac {F_0} {\left[ (k \:-\: m\omega^2)^2 \:+\: c^2\omega ^2 \right]^ {1/2}} \:e^ {-i \phi} \\~\\
\large \phi \:=\: \tan ^{-1} \left( \frac {c\omega} {k\:-\: m\omega ^2} \right)$$

در نتیجه، پاسخ خصوصی به دست می‌آید.

$$\large x_p(t) \:=\: \frac {F_0} {\left[ (k \:-\: m\omega ^2)^2 \:+\: c^2 \omega ^2 \right] ^{1/2}} e^ {i(\omega t\:-\: \phi)}$$

(رابطه ۱1)

اکنون رابطه 10 را بازنویسی می‌کنیم.

$$\large \frac {kX} {F_0} \:=\: \frac {1} {1\:-\: r^2 \:+\: i2 \zeta r} \equiv H(i \omega)$$

در رابطه بالا، $$\large H(i \omega)$$ پاسخ فرکانسی مختلط نامیده می‌شود و مقدار مطلق آن به صورت زیر قابل محاسبه است.

$$\large |H(i \omega)| \:=\: |\frac {kX} {F_0}| \:=\: \frac {1} {\left[ (1\:-\: r^2) ^2 \:+\: (2\zeta r)^2 \right] ^{1/2}}$$

رابطه به دست آمده، مقدار ضریب بزرگ‌نمایی را نشان می‌دهد. با یادآوری $$\large e^ {i \phi}= \cos \phi +i \sin \phi$$، ارتباطی بین دو رابطه اخیر می‌یابیم.

$$\large H(i\omega) \:=\: |H( i\omega)| e^ {-i \phi}$$

اگر زاویه $$\large \phi$$ را به صورت زیر بنویسیم، فرم جدیدی برای پاسخ خصوصی به دست می‌آید.

$$\large \phi\:=\: \tan ^{-1} \left( \frac {2\zeta r} {1\:-\: r^2} \right) \\~\\
\large x_p (t) \:=\: \frac {F_0} {k} |H (i\omega)| e^ {i( \omega t \:-\: \phi)}$$

(رابطه ۱2)

همان‌طور که مشاهده می‌کنید، تابع پاسخ فرکانسی مختلط ($$\large H(i \omega)$$) هر دو مقدار دامنه و فاز مربوط به پاسخ حالت ماندگار را در خود دارد. اگر $$\large F(t) = F_0 \cos \omega t$$ باشد، پاسخ حالت ماندگار متناظر با آن را می‌توانیم با کمک بخش حقیقی رابطه ۱1 بنویسیم.

$$\large x_p (t) \:=\: \frac {F_0} {\left[ (k\:-\: m\omega ^2) ^2 \:+\: c^2 \omega ^2 \right] ^{1/2}} \cos (\omega t \:-\: \phi) \\~\\
\large =\: \text {Re} \left[ \frac {F_0} {k} H(i\omega) e^ {i \omega t} \right] \:=\: \text {Re} \left[ \frac {F_0} {k} |H( i\omega)| e^{i (\omega t \:-\: \phi)} \right]$$

رابطه بالا مشابه رابطه ۲ در ابتدای این مقاله است. به طور مشابه اگر $$\large F(t) =F_0 \sin \omega t$$ باشد، پاسخ حالت ماندگار برابر با قسمت موهومی رابطه ۱1 خواهد بود.

$$\large x_p (t) \:=\: \frac {F_0} {\left[ (k\:-\: m\omega ^2) ^2 \:+\: c^2 \omega ^2 \right] ^{1/2}} \sin (\omega t \:-\: \phi) \\~\\
\large =\: \text {Im} \left[ \frac {F_0} {k} |H( i\omega)| e^{i (\omega t \:-\: \phi)} \right]$$

(رابطه ۱۳)

تحریک هارمونیک و پاسخ سیستم میرا نسبت به آن را می‌توان در صفحه مختلط ارائه کرد. ابتدا از رابطه ۱2 نسبت به زمان مشتق می‌گیریم. معادلات سرعت و شتاب به ترتیب به قرار زیر است.

$$\large \dot {x} _p(t) \:=\: i\omega \frac {F_0} {k} |H (i\omega)| e^ {i( \omega t\:-\: \phi)} \:=\: i\omega x_p (t) \\~\\
\large \ddot {x} _p (t) \:=\: (i\omega) ^2 \frac {F_0} {k} |H(i\omega)| e^ {i (\omega t \:-\: \phi)} \:=\: -\: \omega ^2 x_p (t)$$

می‌دانیم $$\large i$$ به صورت زیر تعریف می‌شود.

$$\large i\:=\: \cos \frac {\pi} {2} \:+\: i\sin \frac {\pi} {2} \:=\: e^ {i \frac {\pi} {2}}$$

می‌بینیم که سرعت نسبت به جابجایی به اندازه $$\large \pi /2$$ جلوتر بوده و مقدارش نیز $$\large \omega$$ برابر شده است. به طور مشابه در مورد $$\large -1$$ نیز می‌توانیم رابطه زیر را بنویسیم.

$$\large -1 \:=\: \cos \pi \:+\: i\sin \pi \:=\: e^ {i\pi}$$

در نتیجه، شتاب نسبت به جابجایی به اندازه $$\large \pi$$ جلوتر بوده و مقدار آن نیز $$\large \omega ^2$$ برابر شده است.

بنابراین، عبارت‌های مختلف به کار رفته در رابطه 9 را می‌توان در صفحه مختلط نشان داد. این موضوع را در شکل زیر به خوبی مشاهده می‌کنید. این شکل به این صورت تفسیر می‌شود که برآیند بردارهای مختلط $$\large m\ddot {x} (t)$$، $$\large c\dot {x} (t)$$ و $$\large kx (t)$$ در تحریک هارمونیک روی $$\large F (t)$$ منطبق می‌شوند تا رابطه ۹ نیز رعایت شده باشد. نکته دیگری که باید به آن توجه کرد، این است که کل نمودار با سرعت زاویه‌ای $$\large \omega$$ در صفحه اعداد مختلط در حال چرخش است. اگر فقط بخش حقیقی پاسخ را در نظر بگیریم، تمام نمودار روی محور حقیقی تصویر می‌شود. در سوی مقابل نیز اگر قرار باشد فقط بخش موهومی را در نظر بگیریم، باید تمام نمودار را روی محور موهومی تصویر کنیم.

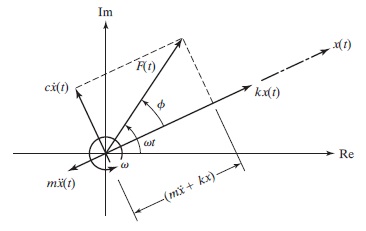
همان‌طور که در شکل بالا مشاهده می‌کنید، نیروی $$\large F (t)= F_0 e^ {i\omega t}$$ به عنوان برداری با زاویه $$\large \omega t$$ نسبت به محور حقیقی رسم شده است. یعنی $$\large F_0$$ یک مقدار حقیقی است. اگر $$\large F_0$$ دارای بخش موهومی هم بود، بردار نیروی $$\large F(t)$$ باید در زاویه $$\large (\omega + \psi)$$ قرار می‌گرفت. در چنین حالتی، تمام بردارهای دیگر نیز به اندازه زاویه $$\large \psi$$ تغییر می‌کردند.

ارتعاشات اجباری با تحریک هارمونیک جابجایی

در برخی اوقات، پایه یا تکیه‌گاه سیستم جرم، فنر و میراگر، در معرض تحریک هارمونیک قرار می‌گیرد. به شکل زیر توجه کنید. فرض کنید جابجایی پایه را با $$\large y(t)$$ و جابجایی جرم را با $$\large x(t)$$ نشان دهیم. این پارامترها جابجایی را در زمان $$\large t$$ و نسبت به تعادل استاتیکی نشان می‌دهند. از این رو، میزان کشیدگی فنر با $$\large x-y$$ و سرعت نسبی بین دو انتهای میراگر نیز با $$\large \dot {x} -\dot {y}$$ برابر است. با توجه به نمودار جسم آزاد رسم شده (قسمت ب)، معادله حرکت را برای چنین سیستمی می‌نویسیم.

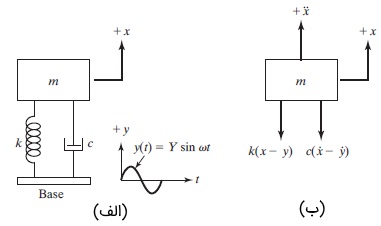
$$\large m\ddot {x} \:+\:c (\dot {x} \:-\: \dot {y}) \:+\:k (x \:-\: y) \:=\: 0$$

اگر $$\large y(t) =Y \sin \omega t$$ برقرار باشد، رابطه بالا به شکل زیر بازنویسی می‌شود.

$$\large m\ddot {x} \:+\: c\dot {x} \:+\: kx \:=\: ky \:+\: c\dot {y} \:=\: kY \sin \omega t \:+\: c\omega Y\cos \omega t \\~\\
\large =\: A\:\sin (\omega t\:-\: \alpha)$$

در رابطه بالا از پارامترهای $$\large A= Y\sqrt {k^2 + (c \omega)^2}$$ و $$\large \alpha =\tan ^{-1} \left[ -\frac {c \omega} {k} \right]$$ استفاده کرده‌ایم. همان‌طور که می‌بینید، تحریک هارمونیک پایه، با تحریک هارمونیک نیرویی معادل است که در آن، بزرگی نیروی وارد به جرم برابر $$\large A$$ باشد. با استفاده از پاسخ $$\large x_p (t)$$ برای رابطه ۱۳، پاسخ به شکل زیر نوشته می‌شود.

$$\large x_p (t) \:=\: \frac {Y \sqrt {k^2 \:+\: (c\omega) ^2}} {\left[ (k\:-\: m\omega ^2) ^2 \:+\: (c\omega) ^2 \right] ^{1/2}} \sin (\omega t \:-\: \phi _1 \:-\: \alpha) \\~\\
\large \phi_1 \:=\: \tan ^{-1} \left( \frac {c\omega} {k \:-\: m\omega ^2} \right)$$

پاسخ $$\large x_p (t)$$ را می‌توانیم به صورت خلاصه نشان دهیم.

$$\large x_p (t) \:=\: X\sin (\omega t \:-\: \phi)$$

(رابطه ۱۴)

ضرایب رابطه بالا به شیوه زیر تعریف می‌شود.

$$\large \frac {X} {Y} \:=\: \left[ \frac {k^2 \:+\: (c\omega) ^2} {(k\:-\: m\omega ^2) ^2 \:+\: (c\omega) ^2} \right] ^{1/2} \:=\: \left[ \frac {1\:+\: (2\zeta r) ^2} {(1\:-\: r^2) ^2 \:+\: (2\zeta r) ^2} \right] ^{1/2} \\~\\
\large \phi \:=\: \tan ^{-1} \left[ \frac {mc \omega ^3} {k(k\:-\: m\omega ^2) \:+\: (\omega c) ^2} \right] \:=\: \tan ^{-1} \left[ \frac {2\zeta r^3} {1\:+\: (4\zeta ^2 \:-\: 1) r^2} \right]$$

نسبت پاسخ $$\large x_p (t)$$ به جابجایی پایه $$\large y(t)$$‌ را قابلیت انتقال جابجایی (Displacement Transmissibility) نامیده و با $$\large \frac {X} {Y}$$ نشان می‌دهیم. شکل زیر، تغییرات $$\large \frac {X} {Y}$$ و $$\large \phi$$ را مطابق با دو رابطه اخیر برای مقادیر مختلف $$\large r$$ و $$\large \zeta$$ نشان می‌دهد.

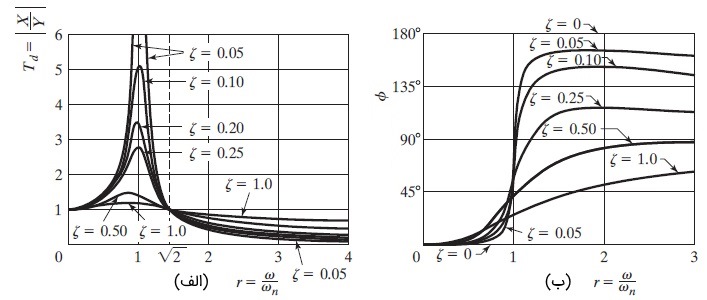
در نظر داشته باشید که اگر تحریک هارمونیک پایه به صورت مختلط $$\large y(t) = \text {Re} (Y e^ {i\omega t})$$ بیان شود، می‌توانیم پاسخ سیستم را براساس آنچه پیش‌تر در بخش «پاسخ سیستم میرا به نیروی مختلط» گفتیم، نشان دهیم.

$$\large x_p (t) \:=\: \text {Re} \left\{ \left( \frac {1\:+\: i2 \zeta r} {1\:-\: r^2 \:+\: i2\zeta r} \right) Ye^ {i\omega t} \right\}$$

در این صورت، قابلیت انتقال جابجایی با کمک رابطه زیر محاسبه خواهد شد.

$$\large \frac {X} {Y} \:=\: T_d \:=\: \left[ 1\:+\: (2\zeta r) ^2 \right] ^{1/2} \times |H(i\omega)|$$

با دقت در شکل بالا، نکات زیر در مورد قابلیت انتقال جابجایی قابل استخراج است.

• مقدار $$\large T_d$$ در $$\large r=0$$ برابر با یک و برای مقادیر کوچک $$\large r$$، نزدیک به یک است.
• در تحریک هارمونیک یک سیستم نامیرا ($$\large \zeta=0$$)، در حالت رزونانس یا تشدید که رابطه $$\large r=1$$ برقرار می‌شود، $$\large T_d$$ به سمت بینهایت میل می‌کند.
• برای مقادیر $$\large r> \sqrt {2}$$ صرف نظر از میزان $$\large \zeta$$، قابلیت انتقال جابجایی از یک کوچکتر است ($$\large T_d <1$$).
• اگر $$\large r= \sqrt {2}$$ باشد، آنگاه برای تمام مقادیر $$\large \zeta$$، قابلیت انتقال جابجایی برابر با یک است.
• در بازه $$\large r< \sqrt {2}$$ نسبت‌های میرایی کوچکتر، به مقادیر $$\large T_d$$ بزرگتری ختم می‌شوند و در سوی مقابل و در بازه $$\large r> \sqrt {2}$$، نسبت‌های میرایی کوچکتر، مقادیر کوچکتری از $$\large T_d$$ را در پی خواهند داشت.
• پارامتر $$\large T_d$$ در بازه $$\large 0< \zeta <1$$ و در نسبت فرکانس $$\large r=r_m <1$$ به ماکزیمم مقدار خود می‌رسد. مقدار این نسبت فرکانس برابر با عبارت زیر است.

$$\large rm \:=\: \frac {1} {2\zeta} \left[ \sqrt {1\:+\: 8\zeta ^2} \:-\: 1 \right] ^{1/2}$$

نیروی انتقالی در تحریک هارمونی با جابجایی پایه

در شکل ۱، به دلیل عکس‌العمل فنر و میراگر، نیروی $$\large F$$ به پایه وارد می‌شود. این نیرو را می‌توان به صورت زیر تعریف کرد.

$$\large F\:=\: k(x\:-\: y) \:+\: c(\dot {x} \:-\: \dot {y}) \:=\: -\: m\ddot {x}$$

با مقایسه رابطه بالا و رابطه 14، نیروی $$\large F$$ را بازنویسی می‌کنیم.

$$\large F\:=\: m\omega ^2X \sin (\omega t \:-\: \phi) \:=\: F_T \sin (\omega t \:-\: \phi)$$

دامنه یا ماکزیمم مقدار نیروی انتقالی در تحریک هارمونیک به پایه به صورت زیر به دست می‌آید.

$$\large \frac {F_T} {kY} \:=\: r^2 \left[ \frac {1\:+\: (2\zeta r) ^2} {(1\:-\: r^2) ^2 \:+\: (2\zeta r) ^2} \right] ^{1/2}$$

نسبت $$\large \frac {F_T} {kY}$$ تحت عنوان قابلیت انتقال نیرو (Force Transmissibility) شناخته می‌شود. توجه کنید که نیروی انتقالی و جابجایی $$\large x(t)$$ هم‌فاز هستند. نمودار تغییرات نیروی انتقالی به پایه را می‌توان برحسب نسبت فرکانس $$\large r$$ و برای مقادیر مختلف $$\large \zeta$$ به صورت شکل زیر رسم کرد.

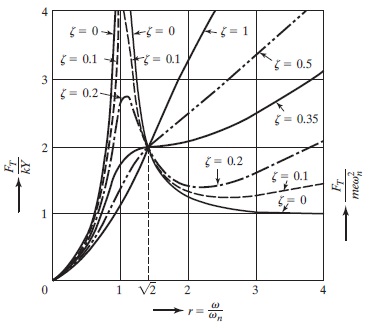
حرکت نسبی در تحریک هارمونیک با جابجایی پایه

فرض کنید جابجایی جرم نسبت به پایه را با $$\large z= x-y$$ نشان دهیم. در این حالت، معادله حرکت به صورت زیر خواهد بود.

$$\large m\ddot {z} \:+\: c\dot {z} \:+\: kz \:=\: -\:m\ddot {y} \:=\: m\omega ^2Y \sin \omega t$$

پاسخ حالت ماندگار معادله بالا به صورت زیر است.

$$\large z(t) \:=\: \frac {m\omega ^2Y \sin (\omega t \:-\: \phi_1)} {\left[ (k\:-\: m\omega ^2) ^2 \:+\: (c\omega) ^2 \right] ^{1/2}} \:=\: Z\: \sin (\omega t \:-\: \phi_1)$$

در رابطه بالا، دامنه و فاز $$\large z(t)$$ را به ترتیب با $$\large Z$$ و $$\large \phi_1$$ نشان داده‌ایم.

$$\large Z\:=\: \frac {m\omega ^2Y} {\sqrt {(k\:-\: m\omega ^2) ^2 \:+\: (c\omega) ^2}} \:=\: Y\frac {r^2} {\sqrt {(1\:-\: r^2) ^2 \:+\: (2\zeta r) ^2}} \\~\\
\large \phi_1 \:=\: \tan ^{-1} \left( \frac {c\omega} {k\:-\: m\omega ^2} \right) \:=\: \tan ^{-1} \left( \frac {2\zeta r} {1\:-\: r^2} \right)$$

مثال 2: حرکت اتومبیل روی جاده ناهموار

سؤال: شکل زیر مدل ساده‌ای از یک اتومبیل را نشان می‌دهد که با عبور از یک جاده ناهموار، در راستای عمودی نوسان می‌کند. جرم اتومبیل برابر $$\large 1200 kg$$ است. سیستم تعلیق، فنری با ثابت $$\large 400 kN/m$$ و نسبت میرایی $$\large \zeta =0.5$$ دارد. اگر سرعت اتومبیل $$\large 20km /hr$$ باشد، دامنه جابجایی آن را تعیین کنید. ناهمواری جاده به صورت سینوسی و با دامنه $$\large Y= 0.05 m$$ و طول موج $$\large 6m$$ است.

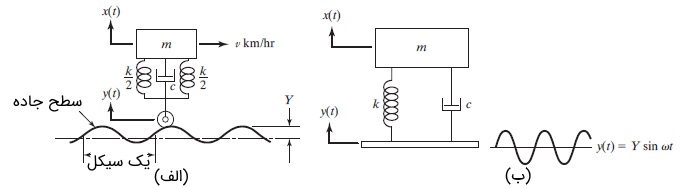
پاسخ: فرکانس $$\large \omega$$ مربوط به تحریک هارمونیک پایه را می‌توان با تقسیم سرعت اتومبیل ($$\large v\: km /hr$$) به طول یک سیکل از ناهمواری جاده به دست آورد.

$$\large \omega\:=\: 2\pi f \:=\: 2\pi \left( \frac {v \times 1000} {3600} \right) \frac {1} {6} \:=\: 0.290889 v \:rad/s$$

برای مقدار $$\large v\:=\: 20\: km /hr$$، فرکانس برابر $$\large \omega\:=\: 5.81778 \:rad /s$$ خواهد بود. فرکانس طبیعی اتومبیل به صورت زیر محاسبه می‌شود.

$$\large \omega_n \:=\: \sqrt {\frac {k} {m}} \:=\: \left( \frac {400 \times 10^3} {1200} \right) ^{1/2} \:=\: 18.2574 \:rad /s$$

حالا می‌توانیم نسبت فرکانس و نسبت دامنه را به دست آوریم.

$$\large r\:=\: \frac {\omega} {\omega _n}\:=\: \frac {5.81778} {18.2574} \:=\: 0.318653 \\~\\
\large \frac {X} {Y}\:=\: \left\{ \frac {1\:+\: (2\zeta r)^2} {(1\:-\: r^2)^2 \:+\: (2\zeta r) ^2} \right\} ^{1/2} \\~\\
\large =\: \left\{ \frac {1\:+\: (2 \times 0.5 \times 0.318653) ^2} {(1\:-\: 0.318653) ^2 \:+\: (2 \times 0.5 \times 0.318653) ^2} \right\} ^{1/2} \:=\: 1.100964$$

بنابراین دامنه جابجایی اتومبیل به صورت زیر خواهد بود.

$$\large X\:=\: 1.100964 Y \:=\: 1.100964 (0.05) \:=\: 0.055048 \:m$$

رابطه بالا نشان می‌دهد که مانعی به ارتفاع $$\large 5\: cm$$ در جاده، شاسی و اتاقک سرنشینان را به اندازه $$\large 5.5\: cm$$ جابجا می‌کند. در نتیجه، سرنشینان یک جابجایی تقویت شده را تجربه خواهند کرد.

مثال ۳: تحریک هارمونیک با پایه ارتجاعی

سؤال: دستگاه سنگینی به وزن $$\large 3000 N$$ روی یک پایه با خاصیت ارتجاعی قرار گرفته است. جابجایی استاتیکی پایه که به دلیل وزن دستگاه ایجاد شده، برابر با $$\large 7.5 cm$$ است. هنگامی که پایه در فرکانس طبیعی سیستم و با دامنه‌ای به بزرگی $$\large 0.25 cm$$‌ در معرض تحریک هارمونیک قرار بگیرد، دامنه ارتعاشات دستگاه $$\large 1\: cm$$ خواهد بود. موارد زیر را تعیین کنید.

الف) ثابت میرایی پایه

ب) اندازه نیروی دینامیکی روی پایه

پ) اندازه جابجایی دستگاه نسبت به پایه

پاسخ: الف) ابتدا با کمک جابجایی استاتیکی، سفتی را به دست می‌آوریم.

$$\large k\:=\: \frac {W} {\delta _{st}} \:=\: \frac {3000} {0.075} \:=\: 40,000 \:N/m$$

در حالت رزونانس ($$\large \omega \:=\: \omega _n$$ یا $$\large r=1$$) قابلیت انتقال جابجایی به صورت زیر است.

$$\large \frac {X} {Y} \:=\: \frac {0.010} {0.0025} \:=\:4\:=\: \left[ \frac {1\:+\: (2\zeta) ^2} {(2\zeta) ^2} \right] ^{1/2} \\~\\
\large \Rightarrow ~~~ \zeta \:=\: 0.1291$$

اکنون می‌توانیم ثابت میرایی را محاسبه کنیم.

$$\large c\:=\: \zeta \times c_c \:=\: \zeta \times 2 \sqrt {km} \:=\: 0.1291 \times 2 \times \sqrt {40,000 \times (3000 /9.81)} \\~\\
\large \Rightarrow ~~~ c\:=\: 903.0512 \:Ns/m$$

ب) اندازه نیروی دینامیکی تحریک هارمونیک روی پایه در $$\large r=1$$ به صورت زیر است.

$$\large F_T \:=\: Yk \left[ \frac {1\:+\: 4\zeta ^2} {4\zeta ^2} \right] ^{1/2} \:=\: kX \:=\: 40,000 \:\times \:0.01 \:=\: 400 \:N$$

پ) جابجایی نسبی دستگاه در $$\large r=1$$‌ نیز به طریق زیر محاسبه می‌شود.

$$\large Z\:=\: \frac {Y} {2\zeta} \:=\: \frac {0.0025} {2\: \times \:0.1291} \:=\: 0.00968 \:m$$

همان‌طور که می‌بینید مقادیر $$\large X$$، $$\large Y$$ و $$\large Z$$ به ترتیب برابر با $$\large 0.01$$، $$\large 0.0025$$ و $$\large 0.00968$$‌ متر به دست آمد و رابطه $$\large Z= X- Y$$ برقرار نیست. زیرا این سه بردار با هم اختلاف فاز دارند.

اگر به مباحث مرتبط در زمینه مکانیک و ارتعاشات علاقه‌مند هستید، آموزش‌های زیر به شما پیشنهاد می‌شوند:

• ژیروسکوپ – از صفر تا صد
• رزونانس – به زبان ساده
• ارتعاشات مکانیکی — بخش سوم: سیستم‌های دو درجه آزادی

^^