توضیح اتحاد جمله مشترک و حل مثال به زبان ساده

اتحاد جمله مشترک، یکی از شناخته‌شده‌ترین اتحادهای جبری است که به فرم استاندارد آن به صورت $$( x + a ) ( x + b ) = x ^ ۲ + ( a + b ) x + a b$$ نوشته می‌شود. از کاربردهای اصلی این اتحاد می‌توان به فاکتورگیری و حل معادلات درجه دو اشاره کرد. در این مطلب از مجله فرادرس، مفهوم اتحاد جمله مشترک را به زبان ساده توضیح می‌دهیم و ضمن مرور کاربردهای این معادله جبری، کاربردهای آن را به همراه حل مثال مورد بررسی قرار می‌دهیم.

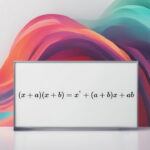
اتحاد در ریاضی چیست؟

«اتحاد» (Identity)، به معادله‌ای گفته می‌شود که به ازای تمام مقادیر، تساوی بین دو طرف آن برقرار باشد. به عنوان مثال، معادله زیر را در نظر بگیرید:

$$( a - b ) ( a + b ) = a ^ ۲ - b ^ ۲$$

این معادله با عنوان اتحاد مزدوج شناخته می‌شود.

اتحادها، انواع مختلفی دارند که از متداول‌ترین آن‌ها می‌توان به «اتحادهای جبری» (Algebraic Identities)، «اتحادهای مثلثاتی» (Trigonometric Identities)، «اتحادهای نمایی» (Exponential Identities) و «اتحادهای لگاریتمی» (Logarithmic Identities) اشاره کرد.

مهم ترین اتحادهای جبری ریاضی کدام هستند؟

از پرکاربردترین اتحادهای ریاضی می‌توان به موارد زیر اشاره کرد:

• اتحاد مربع
  • اتحاد نوع اول یا اتحاد مربع مجموع دو جمله‌ای
  • اتحاد نوع دوم یا اتحاد مربع تفاضل دوجمله‌ای
• اتحاد نوع سوم یا اتحاد مزدوج
• اتحاد نوع چهارم یا اتحاد جمله مشترک
• اتحاد مکعب
  • اتحاد نوع پنجم یا اتحاد مکعب مجموع دوجمله‌ای (اتحاد چاق و لاغر مجموع)
  • اتحاد نوع ششم یا اتحاد مکعب تفاضل دوجمله‌ای (اتحاد چاق و لاغر تفاضل)
• اتحاد نوع هفتم یا اتحاد مربع سه‌جمله‌ای

یکی از مهم‌ترین اتحادهای جبری، اتحاد جمله مشترک است که در ادامه به تعریف آن می‌پردازیم.

اتحاد جمله مشترک چیست؟

اتحاد جمله مشترک، یکی از اتحادهای جبری معروف است که فرم استاندارد آن به صورت زیر نوشته می‌شود:

$$( x + a ) ( x + b ) = x ^ ۲ + ( a + b ) x + a b$$

• $$x$$: یک متغیر و جمله مشترک
• $$a$$ و $$b$$: ثابت‌های عددی یا جمله‌های غیر مشترک

در اتحاد جمله مشترک، $$( x + a )$$ و $$( x + b )$$، دو دوجمله‌ای هستند. بنابراین می‌‌توانیم بگوییم این اتحاد، حاصل‌ضرب دو دوجمله‌ای را نمایش می‌دهد که یک جمله مشترک در بین آن‌ها وجود دارد.

اتحاد جمله مشترک سه جمله ای

اتحاد جمله مشترک سه جمله ای، یکی از فرم‌های اتحاد جمله مشترک است که به صورت زیر نوشته می‌شود:

$$(x + a)(x + b)(x + c)$$

$$=$$

$$x ^ ۳ + ( a + b + c ) x ^ ۲ + ( a b + a c + b c ) x + a b c$$

این اتحاد، ضرب سه دوجمله‌ای را نمایش می‌دهد در بین آن‌ها، یک متغیر یا جمله مشترک (متغیر $$x$$) و سه ثابت یا جمله غیرمشترک ($$b$$ ،$$a$$ و $$c$$) وجود دارد.

فرم های دیگر اتحاد جمله مشترک دو جمله ای

اگر به جای علامت مثبت در میان جمله مشترک $$x$$ و جمله‌های غیرمشترک، علامت منفی وجود داشته باشد، می‌توانیم از به فرم‌های زیر برای نوشتن رابطه اتحاد جمله مشترک استفاده کنیم:

$$( x - a ) ( x + b ) = x ^ ۲ + ( b - a ) x - a b$$

$$( x + a ) ( x - b ) = x ^ ۲ + ( a - b ) x - a b$$

$$( x - a ) ( x - b ) = x ^ ۲ - ( a + b ) x + a b$$

روش‌های مختلفی برای استفاده از اتحاد جمله مشترک دوجمله‌ای و سه‌جمله‌ای وجود دارد. با حل مثال‌ها و تمرین‌های مختلف، می‌توانید به تدریج بر روی این روش‌ها تسلط پیدا کنید.

مثال ۱: تعیین حاصل‌ضرب دو عبارت دو جمله ای

حاصل‌ضرب $$x + ۲$$ در $$x + ۳$$ را به دست بیاورید.

در این مثال، می‌خواهیم حاصل عبارت زیر را به دست بیاوریم:

$$( x + ۲ ) ( x + ۳ )$$

$$x + ۲$$، مجموع دو تک‌جمله‌ای است. بنابراین، می‌توان آن را یک دوجمله‌ای در نظر گرفت. به همین ترتیب، $$x + ۳$$ نیز به عنوان یک دوجمله‌ای در نظر گرفته می‌شود. متغیر $$x$$ در عبارت‌های $$x + ۲$$ و $$x + ۳$$ مشترک است.

بیایید شرایط مسئله را یک بار دیگر مرور کنیم. در این مثال، می‌خواهیم حاصل‌ضرب دو دوجمله‌ای ($$x + ۲$$ و $$x + ۳$$) را به دست بیاوریم که بین این دوجمله‌ای‌ها، یک جمله مشترک ($$x$$) وجود دارد. سریع‌ترین روش برای انجام این کار، استفاده از اتحاد جمله مشترک است. این اتحاد، به صورت زیر نوشته می‌شود:

$$( x + a ) ( x + b ) = x ^ ۲ + ( a + b ) x + a b$$

بر اساس صورت سوال، داریم:

$$a = ۲$$

$$b = ۳$$

این مقادیر را درون اتحاد قرار می‌هیم:

$$( x + ۲ ) ( x + ۳ ) = x ^ ۲ + ( ۲ + ۳ ) x + ۲ \times ۳$$

$$( x + ۲ ) ( x + ۳ ) = x ^ ۲ + ۵ x + ۶$$

به این ترتیب، توانسیم حاصل‌ضرب $$x + ۲$$ در $$x + ۳$$ را به سادگی و با سرعت به دست بیاوریم.

مثال ۲: تعیین حاصل‌ضرب تفاضل تک جمله ای ها

حاصل‌ضرب دو عبارت $$y - ۱$$ و $$y - ۵$$ چه می‌شود؟

در این مثال، می‌خواهیم حاصل ضرب زیر را به دست بیاوریم:

$$( y - ۵ ) ( y - ۱ )$$

ضرب بالا، از دو دوجمله‌ای ($$y - ۱$$ و $$y - ۵$$) با یک جمله مشترک ($$y$$) تشکیل می‌شود. بنابراین، برای انجام آن می‌توانیم از اتحاد جمله مشترک کمک بگیریم. ابتدا این اتحاد را می‌نویسیم:

$$( x + a ) ( x + b ) = x ^ ۲ + ( a + b ) x + a b$$

سپس، بر اساس اطلاعات سوال، تغییر متغیرهای زیر را بر روی معادله بالا اعمال می‌کنیم:

$$x = y$$

$$a = - ۵$$

$$b = - ۱$$

در قدم بعدی، اتحاد جمله مشترک را بر اساس تغییر متغیرهای بالا بازنویسی می‌کنیم:

$$( y - ۵ ) ( y - ۱ ) = y ^ ۲ + ( - ۵ - ۱ ) x + ( - ۵ \times - ۱ )$$

$$( y - ۵ ) ( y - ۱ ) = y ^ ۲ - ۶ x + ۵$$

تا به اینجای این مطلب از مجله فرادرس، فقط به معرفی معادله اتحاد جمله مشترک و کاربرد ساده آن برای ضرب دوجمله‌ای‌ها پرداختیم. این اتحاد، کاربردهای متعددی دارد که می‌تواند شما را در حل بسیاری از مسائل جبر کمک کند. در بخش‌های بعدی، این کاربردها را معرفی کرده و برای هر آن‌‌ها، چند مثال حل می‌کنیم.

اتحاد جمله مشترک به انگلیسی

معادل مستقیمی برای ترجمه عبارت «اتحاد جمله مشترک» در زبان انگلیسی وجود ندارد. البته، برخی از منابع، این اتحاد را در گروه «اتحادهای فاکتورگیری» (Factorization Identities) و برخی در گروه «اتحادهای قضیه بسط دوجمله‌ای» (Binomial Theorem Identities) قرار می‌دهند. در برخی از منابع، از این اتحاد با عنوان «اتحاد نوع چهارم» (Identity IV) و در برخی دیگر با عنوان «اتحاد نوع ششم» (Identity VI) یاد می‌شود. این دسته‌بندی‌ها، به کاربرد برخی از اتحادهای جبری، مخصوصا کاربرد اتحاد جمله مشترک، در فاکتورگیری و تجزیه معادلات به دوجمله‌ای‌ها اشاره دارد. در بخش‌های بعدی، کاربردهای این اتحاد را با حل چند مثال توضیح می‌دهیم.

کاربرد اتحاد جمله مشترک چیست؟

اتحاد جمله مشترک و به طور کلی، تمام اتحادهای جبری، کاربردهای متعددی دارند که از مهم‌ترین آن‌ها می‌توان به ساده‌سازی عبارت‌های جبری، تجزیه (فاکتورگیری)، حل معادله و اثبات دیگر اتحادها اشاره کرد. در ادامه، هر یک از این کاربردها را به همراه حل چند مثال توضیح می‌دهیم.

ساده سازی عبارت های جبری با اتحاد جمله مشترک

یکی از ابتدایی‌ترین کاربردهای اتحاد جمله مشترک، ساده‌سازی عبارت‌های جبری است که از ضرب دوجمله‌ای‌ها تشکیل می‌شوند. مثال‌های ۱ و ۲، مثال‌های ساده‌ای از کاربرد این اتحاد در بازنویسی و ساده‌سازی عبارت‌های جبری بودند. برای آشنایی بیشتر با این کاربرد، یک مثال دیگر را حل می‌کنیم.

مثال ۳: ساده سازی عبارت های جبری

عبارت‌های جبری $$( a + ۱ ) ^ ۲ - ( a - ۲ ) ( a + ۵ )$$ را تا حد ممکن ساده کنید.

$$( a + ۱ ) ^ ۲ - ( a - ۲ ) ( a + ۵ )$$، از اتحاد مربع مجموع دوجمله‌ای $$( a + ۱ ) ^ ۲$$ و اتحاد جمله مشترک $$( a - ۲ ) ( a + ۵ )$$ تشکیل می‌شود. بنابراین برای ساده‌سازی آن، ابتدا این اتحادها را ساده می‌کنیم. اتحاد مربع مجموع دوجمله‌ای عبارت است از:

$$( a + b ) ^ ۲ = a ^ ۲ + ۲ a b + b ^ ۲$$

بر اساس این معادله، داریم:

$$( a + ۱ ) ^ ۲ = a ^ ۲ + ۲ a + ۱$$

اتحاد جمله مشترک نیز به صورت زیر نوشته می‌شود:

$$( x + a ) ( x + b ) = x ^ ۲ + ( a + b ) x + a b$$

بر اساس این اتحاد نیز داریم:

$$( a - ۲ ) ( a + ۵ ) = a ^ ۲ + ۳ a + ۱۰$$

این عبارت‌های ساده شده را درون عبارت مورد سوال قرار می‌دهیم:

$$( a + ۱ ) ^ ۲ - ( a - ۲ ) ( a + ۵ ) = a ^ ۲ + ۲ a + ۱ - \left ( a ^ ۲ + ۳ a - ۱۰ \right)$$

$$( a + ۱ ) ^ ۲ - ( a - ۲ ) ( a + ۵ ) = a ^ ۲ + ۲ a + ۱ - a ^ ۲ - ۳ a + ۱۰$$

$$( a + ۱ ) ^ ۲ - ( a - ۲ ) ( a + ۵ ) = - a + ۱۱$$

به این ترتیب، توانستیم عبارت مورد نظر را با استفاده از اتحاد جمله مشترک و اتحاد مربع مجموع دوجمله‌ای ساده کنیم.

تجزیه عبارت های جبری با اتحاد جمله مشترک

تجزیه در ریاضی، عمل شکستن یک عبارت چندجمله‌ای به صورت مضربی از عبارت‌های دیگر است. به عنوان مثال، فرم استاندارد اتحاد جمله مشترک را در نظر بگیرید:

$$( x + a ) ( x + b ) = x ^ ۲ + ( a + b ) x + a b$$

در این اتحاد، ضرب دو عبارت $$( x + a )$$ و $$( x + b )$$، تجزیه چندجمله‌ای $$x ^ ۲ + ( a + b ) x + a b$$ را نمایش می‌دهد. اتحاد جمله مشترک، یکی از روش‌های تجزیه عبارت‌های جبری محسوب می‌شود. در ادامه، با حل یک مثال، این کاربرد اتحاد جمله مشترک را توضیح می‌دهیم.

مثال ۴: تجزیه معادله درجه دو

در این مثال قصد داریم معادله $$x ^ ۲ + ۵ x - ۶$$ را با استفاده از اتحاد جمله مشترک تجزیه کنیم. به این منظور، ابتدا فرم استاندارد این اتحاد را می‌نویسیم:

$$( x + a ) ( x + b ) = x ^ ۲ + ( a + b ) x + a b$$

سپس، سمت راست اتحاد را با معادله مورد نظر مقایسه می‌کنیم:

$$x ^ ۲ + ( a + b ) x + a b$$

$$x ^ ۲ + ۵ x - ۶$$

همان‌طور که مشاهده می‌کنید، این دو معادله شباهت بسیاری به یکدیگر دارند. تنها وجه تمایز این معادلات، ضرایب آن‌ها است. بنابراین، این ضرایب را با یکدیگر برابر قرار می‌دهیم:

$$a + b = ۵$$

$$a b = - ۶$$

برای مشخص کردن مقادیر $$a$$ و $$b$$، روش‌های متفاوتی وجود دارد. در برخی از مسائل (مانند این مثال)، آزمون و خطا، بهترین و سریع‌ترین روش است. در این روش، برای رسیدن به جواب، فقط باید ببینید کدام دو عدد هستند که ضرب آن‌ها برابر با $$- ۶$$ و جمع آن‌ها برابر با $$۵$$ می‌شود. با امتحان کردن اعداد مختلف، متوجه خواهید شد که این دو عدد، $$- ۱$$ و $$۶$$ هستند. بنابراین، یکی از جمله‌های غیرمشترک را برابر با $$- ۱$$ و دیگری را برابر با $$۶$$ قرار می‌دهیم:

$$a = - ۱$$

$$b = ۶$$

بنابراین، می‌توانیم تجزیه معادله $$x ^ ۲ + ۵ x - ۶$$ را به صورت زیر بنویسیم:

$$x ^ ۲ + ۵ x - ۶ = ( x - ۱ ) ( x + ۶ )$$

در ادامه، یک مثال دشوارتر را حل می‌کنیم.

مثال ۵: تجزیه معادله درجه دو با ضریب

در مثال قبلی، معادله درجه دویی را تجزیه کردیم که ضریب $$x ^ ۲$$ در آن برابر با ۱ بود (اتحاد جمله مشترک، کامل بود). به همین دلیل، فرآیند پیدا کردن جمله‌های مشترک، چالش زیادی نداشت. در این مثال، می‌خواهیم معادله $$۲ x ^ ۲ - ۷ x + ۳$$ را به کمک اتحاد جمله مشترک تجزیه کنیم. به این منظور، فرم استاندارد اتحاد جمله مشترک را می‌نویسیم و طرف راست آن را با معادله مورد نظر مقایسه می‌کنیم:

$$( x + a ) ( x + b ) = x ^ ۲ + ( a + b ) x + a b$$

$$۲ x ^ ۲ - ۷ x + ۳$$

همان‌طور که مشاهده می‌کنید، ضرب $$x ^ ۲$$ در معادله مورد نظر ما، برابر با $$۱$$ نیست. بنابراین نمی‌توانیم برای تجزیه معادله، به دنبال دو عددی بگردیم که مجموع آن‌ها برابر با $$-۷$$ و حاصل‌ضرب‌شان برابر با $$۳$$ شود. از این‌رو، با اعمال یک‌سری تغییرات، معادله $$۲ x ^ ۲ - ۷ x + ۳$$ را به فرم استاندارد اتحاد جمله مشترک نزدیک می‌کنیم. به برای این کار، ابتدا ضریب $$x ^ ۲$$ را مشخص می‌کنیم. این ضریب در معادله $$۲ x ^ ۲ - ۷ x + ۳$$ برابر با $$۲$$ است. در مرحله بعد، معادله را در کسری ضرب می‌کنیم که صورت و مخرج آن، برابر با ضریب $$x ^ ۲$$ است. یعنی:

$$\frac { ۲ } { ۲ } \left ( ۲ x ^ ۲ - ۷ x + ۳ \right )$$

اکنون، صورت کسر را در تمام جمله‌های معادله ضرب می‌کنیم اما مخرج را ثابت نگه می‌داریم:

$$\frac { ۱ } { ۲ } \left ( ۲ \left ( ۲ x ^ ۲ \right ) - ۲ ( ۷ x ) + ۲ ( ۳ ) \right )$$

ضریب $$۲$$ را در جمله درجه دو ($$۲ x ^ ۲$$) و عدد ثابت ($$۳$$) ضرب می‌کنیم اما برای جمله درجه یک ($$۷ x$$)، ضرایب را فقط جابجا می‌کنیم:

$$\frac { ۱ } { ۲ } \left ( ۴ x ^ ۲ - ۷ ( ۲ x ) + ۶ \right )$$

جمله $$۴ x ^ ۲$$ با $$( ۲ x ) ^ ۲$$ تفاوتی ندارد. بنابراین:

$$\frac { ۱ } { ۲ } \left ( \left ( ۲ x \right ) ^ ۲ - ۷ ( ۲ x ) + ۶ \right )$$

اگر به معادله بالا دقت کنید، متوجه شباهت آن با فرم استاندارد اتحاد جمله مشترک خواهید شد. برای درک بهتر این موضوع، تغییر متغیر زیر را انجام می‌دهیم:

$$۲ x = y$$

به این ترتیب، داریم:

$$\frac { ۱ } { ۲ } \left ( y ^ ۲ - ۷ y + ۶ \right )$$

عبارت‌های داخل پرانتز را در نظر بگیرید:

$$y ^ ۲ - ۷ y + ۶$$

برای تجزیه این عبارت، باید دو عددی را پیدا کنیم که مجموع آن‌ها برابر با $$- ۷$$ و حاصلضرب آن‌ها برابر با $$۶$$ باشد. این دو عدد، $$- ۱$$ و $$- ۶$$ هستند. بنابراین می‌توانیم معادله بالا را به صورت زیر تجزیه کنیم:

$$y ^ ۲ - ۷ y + ۶ = ( y - ۱ ) ( y - ۶ )$$

اکنون، یک مرحله به عقب بازمی‌گردیم:

$$\frac { ۱ } { ۲ } \left ( y ^ ۲ - ۷ y + ۶ \right ) = \frac { ۱ } { ۲ } ( y - ۱ ) ( y - ۶ )$$

بر اساس تغییر متغیر، می‌دانیم که:

$$۲ x = y$$

به این ترتیب، داریم:

$$\frac { ۱ } { ۲ } \left ( \left ( ۲ x \right ) ^ ۲ - ۷ ( ۲ x ) + ۶ \right ) = \frac { ۱ } { ۲ } ( ۲ x - ۱ ) ( ۲ x - ۶ )$$

یا

$$۲ x ^ ۲ - ۷ x + ۳ = \frac { ۱ } { ۲ } ( ۲ x - ۱ ) ( ۲ x - ۶ )$$

ضریب $$\frac { ۱ } { ۲ }$$ را به جمله‌های یکی از پرانتزها (به عنوان مثال، جمله‌های پرانتز دوم) اعمال می‌کنیم:

$$۲ x ^ ۲ - ۷ x + ۳ =( ۲ x - ۱ ) ( x - ۳ )$$

در نهایت، معادله مورد نظر، با استفاده از اتحاد، تجزیه می‌شود. مراحل تجزیه معادله درجه دوم به کمک اتحاد جمله مشترک با ضریب را می‌توان به صورت زیر خلاصه کرد:

1. تعیین ضریب جمله درجه دو ($$a$$ در $$a x ^ ۲$$)
2. ضرب کسری با صورت و مخرج ضریب جمله درجه دو (ضرب کسر $$\frac { a } { a }$$) در معادله
3. اعمال صورت کسر در تمام جمله‌های معادله
4. تغییر متغیر معادله برای رسیدن به فرم $$x ^ ۲ + b x + c$$
5. تجزیه معادله درون پرانتز با استفاده از اتحاد
6. برعکس کردن تغییر متغیر
7. ضرب کسر پشت معادله تجزیه شده در یکی از پرانتزها

حل معادلات درجه دو با اتحاد جمله مشترک

در بخش، نحوه استفاده از فرم استاندارد اتحاد جمله مشترک برای تجزیه معادلات درجه دو را آموزش دادیم. روش‌های مختلفی برای حل معادلات درجه دو وجود دارد که متداول‌ترین آن‌ها عبارت هستند از:

• دلتا
• مربع کامل
• فاکتورگیری

یکی از روش‌های فاکتورگیری، تجزیه معادله با استفاده از اتحادهایی نظیر اتحاد جمله مشترک است. پس از اینکه یک معادله را تجزیه کردیم، به دست آوردن ریشه‌های آن بسیار ساده می‌شود و به هیچ فرمول پیچیده‌ای نیاز ندارد. این کاربرد را با حل یک مثال توضیح می‌دهیم.

مثال ۶: ریشه گیری از معادله درجه دو با اتحاد جمله مشترک

معادله درجه دو $$۳ x ^ ۲ + ۱۰ x - ۸ = ۰$$ را در نظر بگیرید. در این مثال، قصد داریم با استفاده از روش اتحاد و تجزیه، ریشه‌های این معادله را به دست بیاوریم. فرم معادله، مشابه فرم استاندارد اتحاد جمله مشترک نبوده و ضریب جمله درجه دو ($$x ^ ۲$$)، برابر با ۱ نیست. بنابراین، طی مراحل زیر، فرم معادله را استاندارد می‌کنیم:

$$\frac { ۳ }{ ۳ } \left ( ۳ x ^ ۲ + ۱۰ x - ۸ \right )$$

$$\frac { ۱ }{ ۳ } \left ( ۳ \left ( ۳ x ^ ۲ \right ) + ۳ ( ۱۰ x ) - ۳ ( ۸ ) \right )$$

$$\frac { ۱ }{ ۳ } \left ( ( ۳ x ) ^ ۲ + ۱۰ ( ۳ x ) - ۲۴ \right )$$

$$۳ x = y$$

$$\frac { ۱ }{ ۳ } \left ( y ^ ۲ + ۱۰ y - ۲۴ \right )$$

اکنون باید دو عددی را بیابیم که جمع‌شان برابر با $$۱۰$$ و حاصل‌ضربشان برابر با $$- ۲۴$$ می‌شود. این دو عدد، $$۱۲$$ و $$- ۲$$ هستند. بنابراین، داریم:

$$\frac { ۱ }{ ۳ } \left ( y ^ ۲ + ۱۰ y - ۲۴ \right ) = \frac { ۱ }{ ۳ } ( y + ۱۲ ) ( y - ۲ )$$

$$\frac { ۱ }{ ۳ } \left ( ( ۳ x ) ^ ۲ + ۱۰ ( ۳ x ) - ۲۴ \right ) = \frac { ۱ }{ ۳ } ( ۳ x + ۱۲ ) ( ۳ x - ۲ )$$

$$۳ x ^ ۲ + ۱۰ x - ۸ = ( x + ۴ ) ( ۳ x - ۲ )$$

$$( x + ۴ ) ( ۳ x - ۲ ) = ۰$$

به این ترتیب، معادله درجه دو را تجزیه کردیم. اکنون می‌توانیم به راحتی، ریشه‌های معادله را به دست بیاوریم. برای این کار، هر یک از پرانتزها را به طور جداگانه برابر با صفر قرار می‌دهیم:

$$x + ۴ = ۰ \to x _ ۱ = - ۴$$

$$۳ x - ۲ = ۰ \to x _ ۲ = \frac { ۲ } { ۳ }$$

در نهایت، توانستیم ریشه‌های معادله درجه دو را بدون استفاده از هیچ فرمولی و فقط به کمک اصول اتحاد و تجزیه به دست بیاوریم.

اثبات اتحاد جمله مشترک

برای اثبات اتحاد جمله مشترک، دو روش ساده وجود دارد که ادامه به آموزش آن‌ها می‌پردازیم.

اثبات اتحاد جمله مشترک به روش اثبات مستقیم

یکی از ساده‌ترین روش‌ها برای اثبات اتحاد جمله مشترک، استفاده از برهان مستقیم است. کار کار، با ساده‌سازی عبارت سمت چپ این اتحاد و رسیدن به عبارت سمت راست آن انجام می‌شود. برای شروع، فرم استاندارد اتحاد را در نظر بگیرید:

$$( x + a ) ( x + b ) = x ^ ۲ + ( a + b ) x + a b$$

می‌خواهیم اثبات کنیم در صورت ساده‌سازی $$( x + a ) ( x + b )$$، به $$x ^ ۲ + ( a + b ) x + a b$$ می‌رسیم. به این منظور، ابتدا حاصل‌ضرب $$( x + a )$$ در $$( x + b )$$ را به دست می‌آوریم. حاصل این ضرب، عبارت است از:

$$( x + a ) ( x + b ) = x \cdot x + x \cdot b + a \cdot x + a \cdot b$$

$$( x + a ) ( x + b ) = x ^ ۲ + b x + a x + a b$$

متغیر $$x$$ در عبارت‌های $$a x$$ و $$b x$$ مشترک است. بنابراین می‌توانیم از آن‌ها فاکتور بگیریم. با فاکتورگیری از $$x$$ خواهیم داشت:

$$( x + a ) ( x + b ) = x ^ ۲ + x ( b + a ) + a b$$

$$( x + a ) ( x + b ) = x ^ ۲ + ( a + b ) x + a b$$

همان‌طور که مشاهده می‌کنید، حاصل‌ضرب $$( x + a )$$ در $$( x + b )$$، عبارت‌های سمت راست اتحاد جمله مشترک را نمایش می‌دهد. به عبارت دیگر، توانستیم از سمت چپ اتحاد به سمت راست آن برسیم و درستی آن را اثبات کنیم.

اثبات اتحاد جمله مشترک با شکل

یکی دیگر از روش‌های اثبات اتحاد جمله مشترک، کمک گرفتن از مفهوم هندسی ضرب است. برای این کار، ابتدا یک مستطیل را در نظر بگیرید.

فرض کنید طول این مستطیل برابر با $$x + a$$ و عرض آن برابر با $$x + b$$ است.

مساحت مستطیل، از ضرب طول در عرض آن به دست می‌آید. بنابراین، مساحت مستطیل بالا برابر است با:

$$( x + a ) ( x + b )$$

اکنون، طول و عرض مستطیل را می‌توانیم به صورت زیر نمایش می‌دهیم.

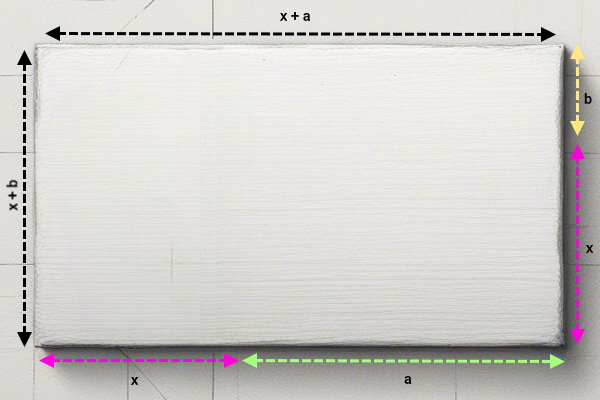
مستطیل را بر اساس اندازه‌های بالا به چند مستطیل کوچک‌تر تقسیم می‌کنیم.

مساحت هر یک از مستطیل‌های کوچک را روی آن‌ها می‌نویسیم.

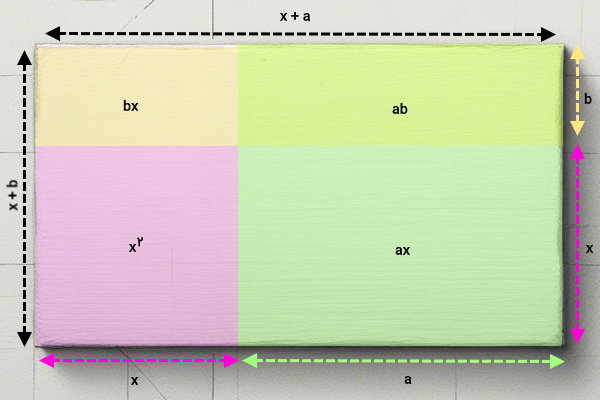
می‌دانیم که مساحت مستطیل بزرگ ($$( x + a ) ( x + b )$$) با مجموع مساحت‌های کوچک درون آن برابر است. به عبارت دیگر:

$$( x + a ) ( x + b ) = a x + a b + x ^ ۲ + b x$$

معادله بالا را مرتب و از عبارت‌های مشترک فاکتورگیری می‌کنیم:

$$( x + a ) ( x + b ) = x ^ ۲ + ( a + b ) x + a$$

این معادله، همان اتحاد جمله مشترک است. به این ترتیب توانستیم معادله این اتحاد را با شکل اثبات کنیم.

سوالات متداول در رابطه با اتحاد جمله مشترک

در بخش انتهایی این مطلب مجله فرادرس، به برخی از پرتکرارترین سوالات در رابطه با اتحاد جمله مشترک به طور خلاصه پاسخ می‌دهیم.

تعریف اتحاد جمله مشترک چیست؟

اتحاد جمله مشترک، معادله‌ای است که حاصل‌ضرب دو دوجمله‌ای را نمایش می‌دهد. بین این دوجمله‌ای‌ها، یک جمله مشترک و دو جمله غیرمشترک وجود دارد.

اتحاد جمله مشترک سه جمله ای چیست؟

اتحاد جمله مشترک سه‌جمله‌ای، معادله‌ای است که حاصل‌ضرب سه دوجمله‌ای را نمایش می‌دهد. بین این دوجمله‌ای‌ها، یک جمله مشترک و سه جمله غیرمشترک وجود دارد.

اتحاد جمله مشترک به صورت کلامی چه می شود؟

اتحاد جمله مشترک دوجمله‌ای به صورت کلامی، جمله مشترک به توان ۲ به علاوه ضرب مجموع جملات غیرمشترک در جمله مشترک به علاوه ضرب جملات غیر مشترک در یکدیگر است.

اتحاد جمله مشترک ناقص چیست؟

هنگامی که ضریب جمله درجه دو (ایکس به توان دو) در معادله درجه دو، برابر با ۱ نباشد، در تجزیه معادله، اتحاد جمله مشترک ناقص به وجود می‌آید.

اتحاد جمله مشترک چه کاربردی دارد؟

کاربرد اصلی اتحاد جمله مشترک، تعیین حاصل‌ضرب دوجمله‌ای‌ها، تجزیه و ریشه‌گیری از معادلات است.