آموزش هوش مصنوعی در متلب – از صفر تا صد + برنامه نویسی

نرم افزار «متلب» (MATLAB) پیاده‌سازی برنامه‌های «هوش مصنوعی» (Artificial Intelligence) را آسان‌تر می‌سازد. متلب با برنامه‌های کاربردی هوش مصنوعی و همچنین ابزارها و توابع اختصاصی مدیریت داده، محیطی ایده‌آل برای به‌کارگیری روش‌های هوش مصنوعی و تجزیه و تحلیل داده‌ها به حساب می‌آید. علاوه بر آن در توسعه یک سیستم کاملاً مهندسی شده، متلب جزو معدود نرم‌افزارها و زبان‌های برنامه‌نویسی است که امکان یکپارچه‌سازی هوش مصنوعی را با «گردش کار» (Workflow) کامل فراهم می‌کند. در این نوشتار به منظور آموزش هوش مصنوعی در متلب مثال‌های متعددی را شرح داده‌ایم و کدهای مربوط به آن‌ها نیز ارائه شده‌اند. مراحل صفر تا صد توسعه روش‌ها و الگوریتم‌های هوش مصنوعی، از بارگذاری داده‌ها تا استقرار مدل‌ها در این مثال‌ها توضیح داده می‌شود.

امکانات و مزایای متلب برای هوش مصنوعی

با متلب، مهندسان و «دانشمندان داده» (Data Scientists) به توابع از پیش ساخته شده، جعبه ابزارهای گسترده و برنامه‌های کاربردی تخصصی برای «طبقه‌بندی» (Classification)، «رگرسیون» (Regression)، «خوشه‌بندی» (Clustering) و دیگر موارد دسترسی فوری دارند. برخی از امکانات و مزایای متلب در توسعه مسائل هوش مصنوعی شامل موارد زیر می‌شود.

• «استخراج ویژگی‌ها» (Feature Extraction) از سیگنال‌ها و تصاویر با استفاده از روش‌های دستی و خودکار تعیین شده و انتخاب خودکار ویژگی‌ها برای فشرده‌تر کردن مدل‌ها
• بهینه‌سازی ویژگی‌ها با استفاده از روش‌های مختلف مهندسی ویژگی
• امکان مقایسه رویکردهایی مانند «رگرسیون لجستیک» (Logistic Regression)، «درخت تصمیم» (Decision Tree)، «ماشین‌ بردار پشتیبان» (Support Vector Machine)، روش‌های جمعی و «یادگیری عمیق» (Deep Learning)
• امکان پیاده‌سازی AutoML به منظور بهینه‌سازی مدل‌ها با استفاده از روش‌های کاهش و تنظیم «فراپارامتر» (Hyperparameter)
• امکان یکپارچه‌سازی مدل‌های «یادگیری ماشین» (Machine Learning) در سیستم‌های سازمانی، خوشه‌ها و ابرها و همچنین امکان ادغام مدل‌های هدف با سخت‌افزار بلادرنگ تعبیه شده
• تولید خودکار کدها برای تحلیل حسگرهای تعبیه شده
• پشتیبانی گردش کار یکپارچه از مرحله تجزیه و تحلیل داده گرفته تا استقرار

هوش مصنوعی چگونه کار می‌کند ؟

هوش مصنوعی در حالت کلی با استفاده از الگوریتم‌های یادگیری ماشین و روش‌های «بهینه‌سازی ریاضیاتی» (Mathematical Optimization) عمل می‌کند. یادگیری ماشین از دو روش «یادگیری نظارت شده» (Supervised Learning) و «یادگیری بدون نظارت» (Unsupervised Learning) برای دسته‌بندی و خوشه‌بندی داده‌ها استفاده می‌کند. یادگیری با نظارت مدلی را روی داده‌های ورودی و خروجی شناخته شده آموزش می‌دهد تا بتواند خروجی‌ها را در نمونه‌های جدید پیش‌بینی کند. یادگیری بدون نظارت الگوهای پنهان یا ساختارهای درونی را در داده‌های ورودی پیدا می‌کند.

بهینه سازی ریاضیاتی فرایندی است که در آن بهترین جواب از میان مجموعه‌ای از جواب‌های ممکن، برای یک مسأله خاص انتخاب می‌شود. بیشتر بهینه‌سازی‌های دنیای واقعی بسیار غیرخطی، چندوجهی و همراه با قیدهای پیچیده هستند. الگوریتم‌های «فرا ابتکاری» (Metaheuristic) نوعی از الگوریتم‌های «تصادفی» (Randomized Algorithems) هستند که برای یافتن پاسخ بهینه به‌کار می‌روند. برخی از الگوریتم‌های شاخص فرا ابتکاری شامل «الگوریتم‌های ژنتیک» (Genetic Algorithm)، «بهینه‌سازی کلونی مورچه‌ها» (Ant Colony Optimization Algorithms)، «ازدحام ذرات» (Particle Swarm) و دیگر موارد است.

پیش از شروع آموزش هوش مصنوعی در متلب ابتدا شرح مختصری برای هر یک از روش‌های مورد استفاده در هوش مصنوعی و یادگیری ماشین در زیربخش‌های بعدی ارائه شده است.

فیلم آموزش شبکه های عصبی مصنوعی در متلب در فرادرس

کلیک کنید

یادگیری با نظارت در هوش مصنوعی چیست ؟

یادگیری تحت نظارت مدلی را ایجاد می‌کند که بر اساس شواهد می‌تواند عمل «پیش‌بینی» (Prediction) را انجام دهد. یک الگوریتم یادگیری با نظارت مجموعه‌ای شناخته شده از داده‌های ورودی و پاسخ‌ها به آن داده‌ها را می‌گیرد و مدلی را به منظور ایجاد پیش‌بینی‌های منطقی برای پاسخ به داده‌های جدید آموزش می‌دهد. یادگیری نظارت شده از روش‌های طبقه‌بندی و رگرسیون برای توسعه مدل‌های یادگیری ماشین استفاده می‌کند.

روش‌های طبقه‌بندی یا همان Classification پاسخ‌های گسسته را پیش‌بینی می‌کنند. تشخیص ایمیل واقعی از هرزنامه و تشخیص تومور سرطانی خوش‌خیم از بدخیم مثال‌هایی از طبقه‌بندی در یادگیری ماشین هستند. مدل‌های طبقه‌بندی، داده‌های ورودی را در دسته‌های مختلف طبقه‌بندی می‌کنند. برخی از کاربردهای دسته‌بندی شامل تصویربرداری پزشکی، «بازشناسی گفتار» (Speech Recognition) و امتیازدهی اعتباری است.

اگر داده‌ها قابل برچسب‌گذاری و دسته‌بندی باشند یا قابلیت تفکیک به گروه‌ها یا کلاس‌های خاصی را داشته باشند، از طبقه‌بندی استفاده می‌شود. به عنوان مثال، برخی برنامه‌های کاربردی به منظور تشخیص متون دست‌نویس از طبقه‌بندی برای تشخیص حروف و اعداد استفاده می‌کنند. در «پردازش تصویر» (Image Processing) و «بینایی کامپیوتر» (Computer Vision) از روش‌های «بازشناسی الگو» (Pattern Recognition) نظارت شده برای «تشخیص اشیا» (Object Detection) و تقسیم‌بندی تصویر استفاده می‌شود.

فیلم آموزش داده کاوی Data Mining در متلب MATLAB در فرادرس

کلیک کنید

طبقه بندی در متلب

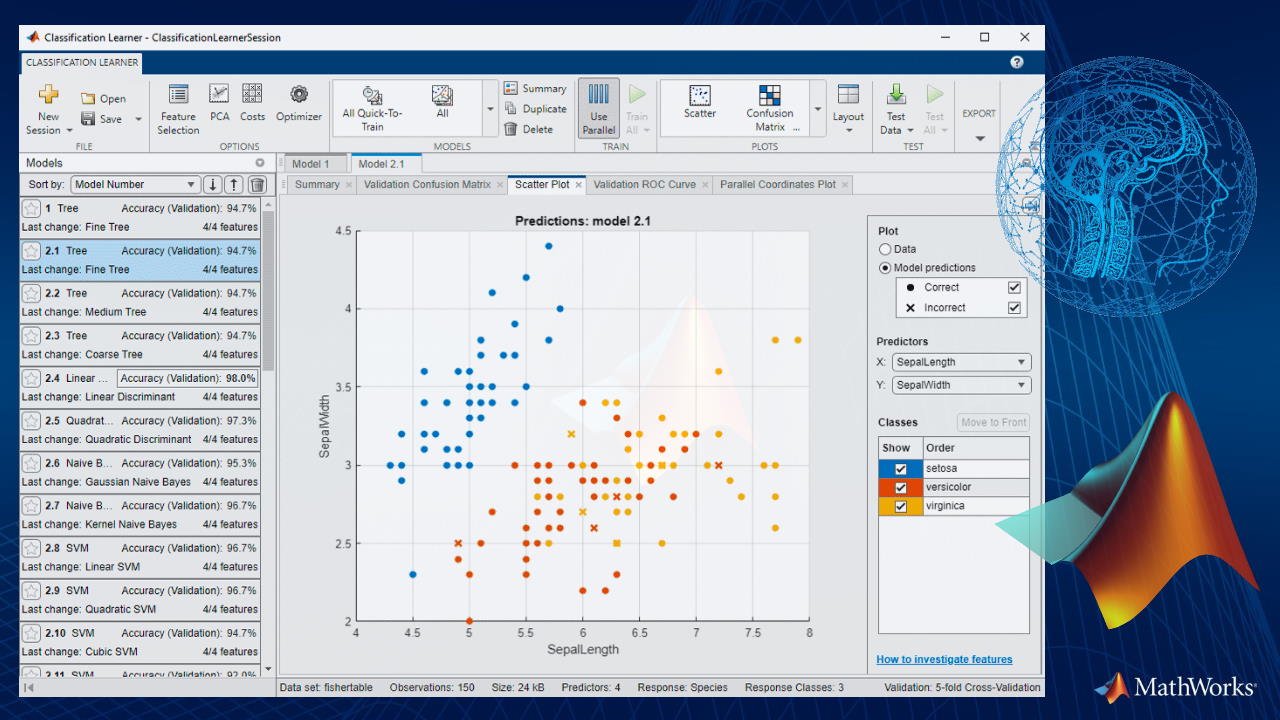
الگوریتم‌های یادگیری تحت نظارت و نیمه نظارتی در مسائل «دودویی» (Binary) و چند کلاسه کاربرد دارند. طبقه‌بندی نوعی از یادگیری ماشینی نظارت شده است که در آن یک الگوریتم «یاد می‌گیرد» تا مشاهدات جدید را با توجه به نمونه‌ داده‌های برچسب‌گذاری شده طبقه‌بندی کند. برای کشف مدل‌های طبقه‌بندی به صورت تعاملی، می‌توان از برنامه کاربردی Classification Learner App در متلب استفاده کرد. در متلب این انعطاف‌پذیری و امکان وجود دارد که بتوان از خط فرمان برای وارد کردن مدل پیش‌بینی‌کننده، برچسب‌ها، داده‌ها و دیگر موارد در قالب یک «تابع برازش» (Fitness Function) استفاده کرد.

رگرسیون در یادگیری با نظارت

در مدل‌سازی آماری، تحلیل رگرسیون مجموعه‌ای از فرآیندهای آماری برای تخمین روابط بین یک متغیر وابسته با یک یا چند متغیر مستقل است. در اصطلاح یادگیری ماشین، متغیر وابسته «برچسب» (Label) نامیده می‌شود. همچنین متغیرهای مستقل، «متغیرهای پیش‌بینی‌کننده» (Predictors)، «متغیرهای کمکی» (Covariates)، «متغیرهای توضیحی» (Explanatory Variables) یا «ویژگی‌ها» (Features) نامیده می‌شوند.

رایج‌ترین شکل تحلیل رگرسیون، «رگرسیون خطی» (Linear Regression) است که در آن به دنبال یک خط (یا ترکیب خطی پیچیده‌تر) هستیم که بیشترین «برازش» (Fitness) را با داده‌ها دارد. جعبه ابزار Statistics and Machine Learning به شما امکان می‌دهد مدل‌های رگرسیون خطی، تعمیم یافته خطی و غیرخطی را برازش کنید. هنگامی که یک مدل رگرسیونی توسعه پیدا کرد، می‌توان از آن برای پیش‌بینی یا شبیه‌سازی پاسخ‌ها، ارزیابی برازش مدل با استفاده از «آزمون‌های فرضیه» (Hypothesis Test)، یا استفاده از نمودارها برای مصورسازی، بررسی «پسماندها» (Residuals) و اثرات متقابل استفاده کرد.

فیلم آموزش شبکه های عصبی مصنوعی در متلب در فرادرس

کلیک کنید

یادگیری بدون نظارت در متلب

یادگیری بدون نظارت الگوهای پنهان یا ساختارهای درونی را در داده‌های بدون برچسب پیدا می‌کند. «خوشه‌بندی» (Clustering) رایج‌ترین روش یادگیری بدون نظارت است که برای تجزیه و تحلیل داده‌های اکتشافی و برای یافتن الگوها یا گروه‌بندی‌های پنهان در داده‌ها استفاده می‌شود. برنامه‌های کاربردی متلب برای تجزیه و تحلیل خوشه‌‌بندی شامل تجزیه و تحلیل توالی ژن، تحقیقات بازار و تشخیص اشیا می‌شود.

خوشه بندی در متلب

تجزیه و تحلیل خوشه‌بندی که به آن تحلیل «بخش‌بندی» (Segmentation) یا «تقسیم‌بندی» (Taxonomy) هم گفته می‌شود، داده‌های نمونه را به گروه‌ها یا خوشه‌ها تقسیم می‌کند. خوشه‌ها به گونه‌ای تشکیل می‌شوند که اشیاء مشابه در یک خوشه قرار می‌گیرند و اشیاء در خوشه‌های مختلف، متمایز هستند. تولباکس Statistics and Machine Learning در متلب چندین روش خوشه‌بندی و معیارهای تشابه را که معیارهای فاصله نیز نامیده می‌شود برای ایجاد خوشه‌ها ارائه می‌دهد.

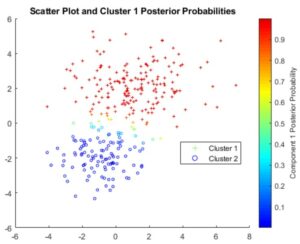
علاوه بر این، در ارزیابی خوشه‌بندی، تعداد بهینه خوشه‌ها با استفاده از معیارهای ارزیابی مختلف تعیین می‌شود. امکان نمایش و مصورسازی خوشه‌ها شامل «دندروگرام‌ها» (Dendrograms) و نمودارهای سیلوئت (Silhouette) و امکان دیگر نمایش‌های گرافیکی وجود دارد. این جعبه ابزار همچنین چندین قابلیت را برای «تشخیص ناهنجاری» (Anomaly Detection) و شناسایی داده‌های «پرت» (Outlier) دارد.

الگوریتم ژنتیک چیست؟

الگوریتم ژنتیک روشی برای حل مسائل بهینه‌سازی مقید و غیرمقید و مبتنی بر انتخاب طبیعی و مطابق با فرآیندی است که تکامل بیولوژیکی را هدایت می‌کند. الگوریتم ژنتیک به طور مکرر جمعیتی از راه‌حل‌های یکتا را تغییر می‌دهد. در هر مرحله، الگوریتم ژنتیک افرادی را از جمعیت فعلی به عنوان والدین انتخاب و از آنها برای تولید فرزندان برای نسل بعدی استفاده می‌کند. در طول نسل‌های متوالی، جمعیت به سمت یک راه حل بهینه «تکامل» می‌یابد.

می‌توان الگوریتم ژنتیک را برای حل آن دسته از مسائل بهینه‌سازی به‌کار برد که حل آن‌ها با استفاده از الگوریتم‌های بهینه‌سازی استاندارد مناسب نیستند، از جمله می‌توان به مسائلی اشاره کرد که در آنها تابع هدف ناپیوسته، مشتق‌ناپذیر، تصادفی یا بسیار غیرخطی است. الگوریتم ژنتیک می‌تواند مسائل برنامه‌نویسی اعداد صحیح مختلط را حل کند، که در آن برخی از مؤلفه‌ها محدود به مقادیر صحیح هستند. نمودار زیر جریان مراحل اصلی الگوریتم ژنتیک را تشریح می‌کند.

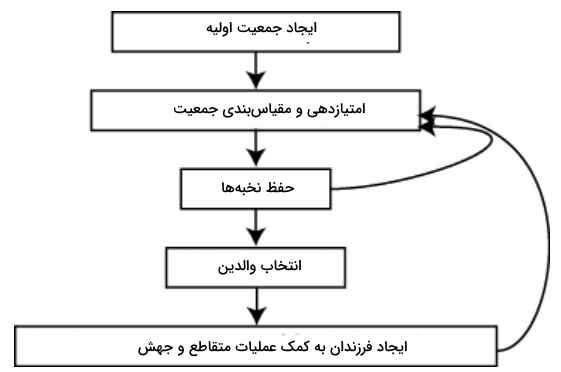
الگوریتم ژنتیک از سه نوع قانون اصلی در هر مرحله برای ایجاد نسل بعدی از جمعیت فعلی استفاده می‌کند که شامل موارد زیر می‌شود.

• قوانین «انتخاب» (Selection)، افرادی را انتخاب می‌کند که والدین نامیده می‌شوند و در نسل بعدی به تولید جمعیت کمک می‌کنند. انتخاب به طور کلی تصادفی است و می‌تواند به نمرات افراد بستگی داشته باشد.
• قوانین «متقاطع» (Crossover)، دو والد را ترکیب می‌کند تا فرزندان نسل بعدی را تشکیل دهند.
• قوانین «جهش» (Mutation)، تغییرات تصادفی را در هر یک از والدین اعمال می‌کند تا فرزندان را تشکیل دهند.

فیلم آموزش الگوریتم ژنتیک در متلب MATLAB در فرادرس

کلیک کنید

آموزش هوش مصنوعی در متلب برای طبقه بندی

در این قسمت از آموزش هوش مصنوعی در متلب ، ابتدا مروری داریم بر الگوریتم‌های طبقه‌بندی و امکاناتی که متلب در این خصوص فراهم کرده است و سپس با ارائه مثال به پیاده‌سازی برخی از این الگوریتم‌ها در محیط کدنویسی متلب خواهیم پرداخت.

الگوریتم‌های طبقه‌بندی و امکانات متلب برای آن ها

فیلم آموزش تشخیص و شناسایی اشیا با شبکه های عصبی در متلب MATLAB

کلیک کنید

• برنامه کاربردی Classification Learner App برای آموزش، اعتبارسنجی و تنظیم مدل‌های طبقه‌بندی
• «درختان طبقه‌بندی» (Classification Trees)
• «تجزیه و تحلیل تشخیصی یا افتراقی» (Discriminant Analysis)
• «بیز ساده» (Naive Bayes)
• «نزدیک‌ترین همسایه‌ها» (Nearest Neighbors)
• «ماشین بردار پشتیبان» (Support Vector Machine)
• «روش‌های جمعی» (Classification Ensembles)
• «مدل افزایشی تعمیم یافته» (Generalized Additive Model)
• «شبکه‌های عصبی» (Neural Networks)
• «یادگیری افزایشی» (Incremental Learning)
• «یادگیری نیمه‌نظارتی» (Semi-Supervised Learning for Classification)
• «انصاف در طبقه‌بندی باینری» (Fairness in Binary Classification)
• «تفسیرپذیری» (Interpretability) به منظور تفسیر مدل‌های دسته‌بندی پیچیده
• «ساخت و ارزیابی مدل» (Model Building and Assessment) شامل انتخاب ویژگی، مهندسی ویژگی، انتخاب مدل، بهینه‌سازی هایپرپارامتر، «اعتبارسنجی متقابل» (Cross Validation)، ارزیابی عملکرد پیش‌بینی‌کننده و آزمون‌های مقایسه دقت طبقه‌بندی

در ادامه یک مجموعه داده شناخته شده، به نام داده‌‌‌های آیریس، را در نظر می‌گیریم و عمل طبقه‌بندی را به کمک برخی از الگوریتم‌های نام برده شده در محیط متلب بر روی این دیتاست پیاده‌سازی می‌کنیم. روش‌ها و الگوریتم‌های به‌کار رفته در این مثال شامل موارد زیر می‌شود.

• تحلیل افتراقی
• دسته‌بند بیز ساده
• دسته‌بند درخت‌ تصمیم

مجموعه داده گل زنبق برای آموزش هوش مصنوعی در متلب

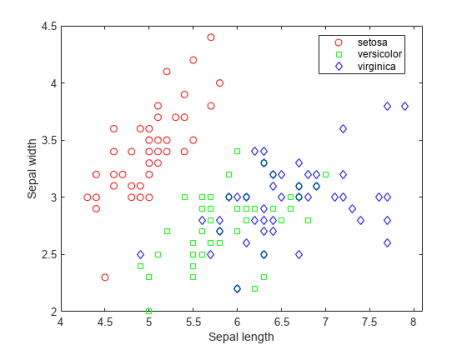
داده‌های گل «زنبق» (Iris) یک مجموعه داده شناخته شده است که در آموزش هوش مصنوعی در متلب، پایتون و دیگر ابزارهای تحلیل هوش مصنوعی بسیار مورد استفاده قرار می‌گیرد. این داده‌ها شامل چهار ویژگی «طول کاسبرگ» (Sepal Length)، «عرض کاسبرگ» (Sepal Width)، «طول گلبرگ» (Petal Length) و «عرض گلبرگ» (Petal Width) برای 150 نمونه گل زنبق است. از قبل می‌دانیم که این مجموعه سه دسته از انواع گونه‌های زنبق را شامل می‌شود و هر دسته شامل 50 نمونه است. در ابتدا باید داده‌ها را بارگذاری کنیم.

1load fisheriris
2f = figure;
3gscatter(meas(:,1), meas(:,2), species,'rgb','osd');
4xlabel('Sepal length');
5ylabel('Sepal width');

کدهای فوق بارگذاری دیتاست (مجموعه داده) و ترسیم نمودار پراکندگی را انجام می‌دهند.

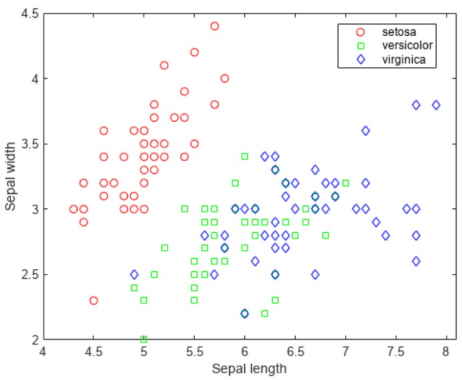
خروجی نمودار پراکندگی را در شکل فوق ملاحظه می‌کنید.

1N = size(meas,1);

در این مسئله قصد داریم با توجه به ارتباط نوع گل با اندازه‌ کاسبرگ و گلبرگ آن، پیش‌بینی کنیم گل‌های جدید از چه نوعی خواهند بود. در ابتدا با استفاده از تحلیل افتراقی (تشخیصی) این مسئله را حل می‌کنیم.

آموزش هوش مصنوعی در متلب برای تحلیل افتراقی

آموزش هوش مصنوعی در متلب را با بررسی آنالیز افتراقی ادامه می‌دهیم. تابع fitcdiscr  می‌تواند طبقه‌بندی را با استفاده از روش‌های مختلف تحلیل افتراقی انجام دهد. ابتدا داده‌ها را با استفاده از تحلیل افتراقی خطی (LDA) طبقه‌بندی می‌کنیم.

1lda = fitcdiscr(meas(:,1:2),species);
2ldaClass = resubPredict(lda);

مشاهدات با برچسب‌های کلاس شناخته شده معمولاً «داده‌های آموزشی» (Training Data) نامیده می‌شوند. «خطای جایگزینی مجدد» (Resubstitution Error) در مجموعه آموزشی برابر است با نسبت مشاهداتی که به اشتباه طبقه‌بندی شده‌اند. در اینجا خطای جایگزینی مجدد را که به آن «خطای طبقه‌بندی اشتباه» (Misclassification Error) هم گفته می‌شود به کمک متلب محاسبه می‌کنیم.

1ldaResubErr = resubLoss(lda)

بنابراین مقدار ldaResubErr برابر با 0.2 خواهد بود. همچنین می‌توان «ماتریس درهم‌ریختگی» (Confusion Matrix) را در مجموعه آموزشی محاسبه کرد. یک ماتریس درهم‌ریختگی حاوی اطلاعاتی در مورد برچسب‌های کلاس شناخته شده و برچسب‌های کلاس پیش‌بینی شده است. به طور کلی، عنصر (i , j) در ماتریس درهم‌ریختگی تعداد نمونه‌هایی است که برچسب کلاس شناخته شده آنها، کلاس i و کلاس پیش‌بینی شده آنها j است. عناصر قطری مشاهداتی هستند که به درستی طبقه‌بندی شده‌اند.

1figure
2ldaResubCM = confusionchart(species,ldaClass);

کدهای فوق نمودار مربوط به ماتریس درهم‌ریختگی را توسعه می‌دهند که تصویر آن در ادامه آمده است.

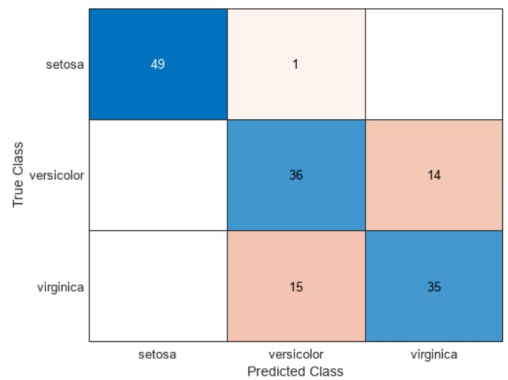
از 150 مشاهده آموزشی، 20٪ مشاهدات (معادل با تعداد 30 مشاهده) توسط تابع افتراقی خطی به اشتباه طبقه‌بندی می‌شوند.

1figure(f)
2bad = ~strcmp(ldaClass,species);
3hold on;
4plot(meas(bad,1), meas(bad,2), 'kx');
5hold off;

با توجه به کد فوق، نمودار پراکندگی به شکل زیر خواهد بود.

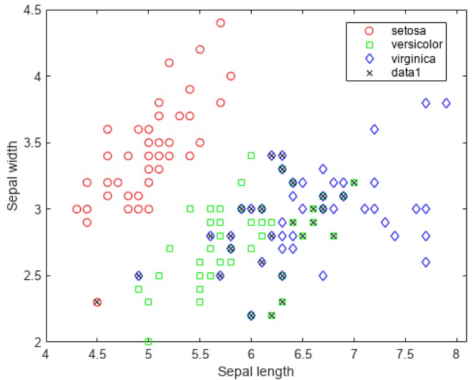
این تابع، صفحه را به ناحیه‌های مختلفی تقسیم می‌کند که با خطوطی از هم جدا شده‌اند و مناطق مختلف را به انواع گونه‌های گل اختصاص می‌دهد. یکی از راه‌های مصورسازی این مناطق، ایجاد شبکه‌ای از مقادیر (x,y) و اعمال تابع طبقه‌بندی در آن شبکه است.

1[x,y] = meshgrid(4:.1:8,2:.1:4.5);
2x = x(:);
3y = y(:);
4j = classify([x y],meas(:,1:2),species);
5gscatter(x,y,j,'grb','sod')

با توجه به کدهای فوق، ناحیه‌بندی خوشه‌ها به شکل زیر خواهد بود.

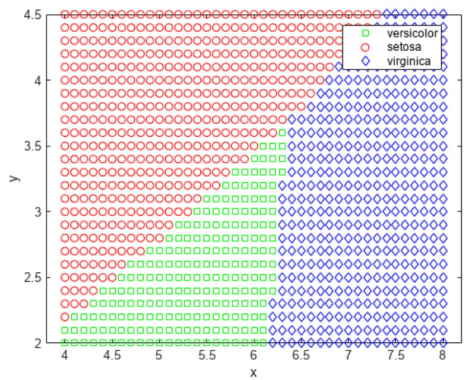
در ادامه این مطلب به بحث آموزش هوش مصنوعی در متلب برای تحلیل افتراقی درجه دوم پرداخته‌ایم، اما پیش از آن مجموعه دوره‌های آموزش هوش مصنوعی فرادرس به مخاطبان معرفی شده است.

معرفی فیلم های آموزش هوش مصنوعی

مجموعه‌های آموزشی فرادرس حاوی تعدادی دوره‌های ویدیویی هستند که برای یک موضوع آموزشی خاص تدوین شده‌اند. پلتفرم فرادرس با در نظر گرفتن نیازهای دانشگاهی و بازار کار اقدام به انتشار این مجموعه‌های کاربردی و عملیاتی کرده است. مجموعه آموزش‌های هوش مصنوعی نیز با در نظر گرفتن مهارت‌های برنامه‌نویسی‌ مرتبط با آن‌ها به ویژه زبان برنامه‌نویسی متلب، علوم زیرمجموعه‌ همچون یادگیری ماشین، یادگیری عمیق، داده‌کاوی و دیگر موارد را از سطوح مبتدی تا پیشرفته پوشش می‌دهد. در تصویر بالا تنها به تعداد محدودی از آموزش‌های این مجموعه اشاره شده است.

• برای دسترسی به همه دوره‌های آموزش هوش مصنوعی فرادرس + اینجا کلیک کنید.

آموزش هوش مصنوعی در متلب برای تحلیل افتراقی درجه دوم

در خصوص برخی از داده‌ها، ناحیه‌ها برای کلاس‌های مختلف به‌خوبی توسط خطوط حائل جدا نمی‌شوند. در چنین شرایطی، تحلیل افتراقی خطی مناسب نیست. به جای آن، می‌توان تحلیل افتراقی درجه دوم (QDA) را روی داده‌ها پیاده‌سازی کرد. خطای جایگزینی مجدد در تحلیل تفکیک درجه دوم به کمک متلب به صورت زیر محاسبه می‌شود.

1qda = fitcdiscr(meas(:,1:2),species,'DiscrimType','quadratic');
2qdaResubErr = resubLoss(qda)

در اینجا qdaResubErr برابر با 0.2 می‌شود. خطای تست که به آن «خطای تعمیم» (Generalization Error) نیز گفته می‌شود، برابر با خطای پیش‌بینی انتظاری در یک مجموعه مستقل است. خطای جایگزینی مجدد احتمالاً «خطای تست» (Test Error) را کمتر از حد لازم برآورد می‌کند. در این مورد، مجموعه داده برچسب‌گذاری‌شده دیگری در دسترس نیست، اما می‌توان با انجام اعتبارسنجی متقابل آن را شبیه‌سازی کرد.

اعتبارسنجی متقابلِ 10 بخشی روشی رایج برای تخمین خطای آزمون در الگوریتم‌های طبقه‌بندی است. در این روش، مجموعه آموزشی به طور تصادفی به 10 زیر مجموعه مجزا تقسیم می‌شود. اندازه هر زیرمجموعه تقریباً برابر است و نسبت‌های کلاسی تقریباً مشابهی در مجموعه آموزشی دارد. در این روش، یک زیر مجموعه حذف و مدل طبقه‌بندی، با استفاده از 9 زیر مجموعه دیگر آموزش داده می‌شود.

از مدل آموزش دیده برای طبقه‌بندی زیرمجموعه حذف شده استفاده می‌شود. در هر تکرار، می‌توان این کار را با حذف هر یک از ده زیر مجموعه تکرار کرد. از آنجا که اعتبارسنجی متقابل، داده‌ها را به طور تصادفی تقسیم می‌کند، نتیجه آن به «دانه» (Seed) تصادفی اولیه بستگی دارد. برای بازتولید نتایج دقیق در این مثال، دستور زیر را اجرا می‌کنیم.

1rng(0,'twister');

برای تولید 10 زیر مجموعه از cvpartition استفاده می‌کنیم.

1cp = cvpartition(species,'KFold',10)

خروجی کد فوق به صورت زیر خواهد بود.

روش‌های crossval و kfoldLoss می‌توانند خطای طبقه‌بندی را برای LDA و QDA با استفاده از پارتیشن داده (cp) اشتباه تخمین بزنند. «خطای تست درست» (True Test Error) LDA را با استفاده از اعتبارسنجی متقابل 10 بخشی تخمین می‌زنیم.

1cvlda = crossval(lda,'CVPartition',cp);
2ldaCVErr = kfoldLoss(cvlda)

در اینجا خروجی برابر 0.2 خواهد بود. خطای اعتبارسنجی متقابل LDA برابر با مقدار خطای جایگزینی مجدد LDA است. خطای تست درست برای QDA را با استفاده از اعتبارسنجی متقابل 10 بخشی تخمین می‌زنیم.

1cvqda = crossval(qda,'CVPartition',cp);
2qdaCVErr = kfoldLoss(cvqda

در کدهای فوق مقدار qdaCVErrبرابر با ۰.۲۲ خواهد بود. QDA دارای یک خطای اعتبار متقابل کمی بزرگتر از LDA است. این نشان می‌دهد که یک مدل ساده‌تر عملکرد قابل مقایسه یا بهتری نسبت به یک مدل پیچیده‌تر دارد.

آموزش هوش مصنوعی در متلب برای دسته بند بیز ساده

آموزش هوش مصنوعی در متلب را با بررسی «طبقه‌بند» (کلاسیفایر) بِیز ساده (بِیز ساده‌لوح) ادامه می‌دهیم. تابع fitcdiscr شامل دو نوع دیگر 'DiagLinear' و 'DiagQuadratic' می‌شود. این‌ها شبیه به توابع خطی و درجه دوم هستند، اما با این تفاوت که تخمین‌های ماتریس کوواریانس قطری دارند. این انتخاب‌های قطری نمونه‌های خاصی از یک «دسته‌بند بیز ساده» (Naive Bayese Classifire) هستند. در طبقه‌بندی بیز فرض می‌شود که متغیرها با توجه به برچسب کلاس مستقل هستند. طبقه‌بندی کننده‌های بیز ساده از رایج‌ترین طبقه‌بندی کننده‌ها هستند. علی رغم این که فرض استقلال شرطی کلاس بین متغیرها به طور کلی درست نیست، طبقه‌بندی‌کننده‌های بیز ساده در عمل در بسیاری از مجموعه‌ داده‌ها به‌خوبی کار می‌کنند.

می‌توان از تابع fitcnb برای ایجاد یک نوع کلی‌ از دسته‌بند بیز ساده استفاده کرد. ابتدا هر متغیر در هر کلاس را با استفاده از توزیع گاوسی مدل و خطای جایگزینی مجدد و خطای اعتبارسنجی متقابل محاسبه می‌کنیم.

1nbGau = fitcnb(meas(:,1:2), species);
2nbGauResubErr = resubLoss(nbGau)

در کدهای فوق، مقدار nbGauResubErr برابر با ۰.۲۲ خواهد بود.

1nbGauCV = crossval(nbGau, 'CVPartition',cp);
2nbGauCVErr = kfoldLoss(nbGauCV)

مقدار nbGauCVErr نیز در کدهای فوق برابر با ۰.۲۲ می‌شود.

1labels = predict(nbGau, [x y]);
2gscatter(x,y,labels,'grb','sod')

با توجه به کد فوق، ناحیه‌بندی خوشه‌ها به شکل زیر خواهد بود.

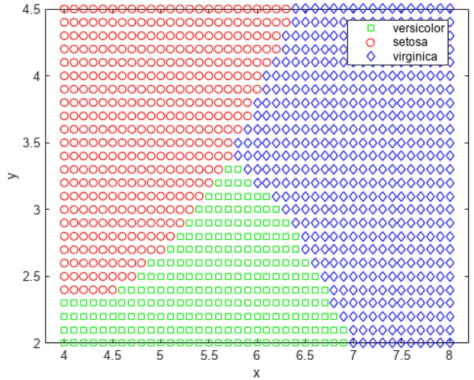
تا اینجا فرض کرده بودیم که متغیرهای هر کلاس دارای توزیع نرمال چند متغیره هستند. اغلب این یک فرض معقول است، اما گاهی اوقات ممکن است این فرض معتبر نباشد. اکنون هر متغیر را در هر کلاس با استفاده از یک تخمین چگالی هسته مدل می‌کنیم. این رویکرد یک روش ناپارامتریک است و انعطاف‌پذیرتری بیشتری دارد.

1nbKD = fitcnb(meas(:,1:2), species, 'DistributionNames','kernel', 'Kernel','box');
2nbKDResubErr = resubLoss(nbKD)

مقدار nbKDResubErr برابر با ۰.۲۰۶۷ می‌شود.

1nbKDCV = crossval(nbKD, 'CVPartition',cp);
2nbKDCVErr = kfoldLoss(nbKDCV)

در اینجا مقدار ۰.۲۱۳۳ در متغیر nbKDCVErr ذخیره می‌شود.

1labels = predict(nbKD, [x y]);
2gscatter(x,y,labels,'rgb','osd')

با توجه به کد فوق، ناحیه‌بندی خوشه‌ها به شکل زیر خواهد بود.

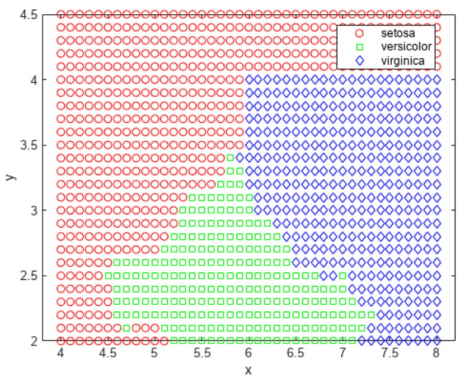
برای این مجموعه داده، طبقه‌بندی کننده بیز ساده با تخمین چگالی هسته در مقایسه با طبقه‌بندی کننده بیز ساده با توزیع گاوسی، خطای جایگزینی مجدد و خطای اعتبار متقابل کمتری دریافت می‌کند.

آموزش هوش مصنوعی در متلب برای درخت تصمیم

در این بخش از آموزش هوش مصنوعی در متلب، به دسته‌بند «درخت تصمیم» (Decision Tree) می‌پردازیم و نحوه پیاده‌سازی آن را شرح می‌دهیم. درخت تصمیم شامل مجموعه‌ای از قوانین ساده است؛ برای نمونه، یک قانون در مثال اخیر را می‌توان به این شکل بیان کرد که «اگر طول کاسبرگ کمتر از 5.45 باشد، نمونه در کلاس setosa قرار خواهد داشت». درختان تصمیم نیز جز الگوریتم‌های ناپارامتریک محسوب می‌شوند، زیرا کلاس‌ها به هیچ فرضی در مورد توزیع متغیرها نیاز ندارند. در نرم‌افزار متلب، تابع fitctree  یک درخت تصمیم ایجاد می‌کند. مثال جاری را با استفاده از درخت تصمیم توسعه می‌هیم.

1t = fitctree(meas(:,1:2), species,'PredictorNames',{'SL' 'SW' });

جالب است که ببینیم روش درخت تصمیم چگونه صفحه را تقسیم می‌کند. از همان روش بالا برای مصورسازی مناطق تخصیص داده شده به هر دسته از انواع گل زنبق استفاده می‌کنیم.

1[grpname,node] = predict(t,[x y]);
2gscatter(x,y,grpname,'grb','sod')

تصویر نمودار حاصل شده در ادامه آمده است.

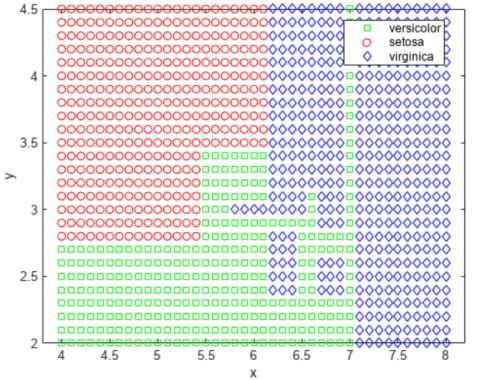
راه دیگر برای مصورسازی درخت تصمیم، ترسیم نمودار قانون تصمیم و تخصیص کلاس است.

1ٰview(t,'Mode','graph');

خروجی خط کد بالا به صورت زیر است.

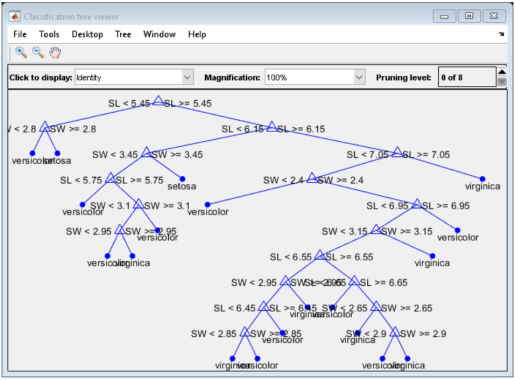
این درخت با ظاهر درهم از قوانینی به شکل «SL < 5.45» برای طبقه‌بندی هر نمونه به یکی از 19 گره پایانه استفاده می‌کند. برای تعیین و تخصیص کلاس در هر مشاهده، از گره بالایی شروع می‌کنیم و قانون را اعمال می‌کنیم. اگر نقطه مطابق با قانون تعریف شده باشد، مسیر چپ را انتخاب می‌کنیم و در غیر این صورت مسیر راست را انتخاب می‌کنیم. در نهایت به یک گره پایانی می‌رسیم که مشاهده را به یکی از سه دسته اختصاص می‌دهد. در ادامه خطای جایگزینی مجدد و خطای اعتبارسنجی متقابل را برای درخت تصمیم محاسبه می‌کنیم.

1dtResubErr = resubLoss(t)

مقدار dtResubErr برابر با ۰.۱۳۳۳ بدست می‌آید.

1cvt = crossval(t,'CVPartition',cp);
2dtCVErr = kfoldLoss(cvt)

مقدار ذخیره شده در dtCVErr برابر با ۰.۳ خواهد بود. مشخص شد که در الگوریتم درخت تصمیم، خطای اعتبارسنجی متقابل به طور قابل توجهی بزرگتر از خطای جایگزینی است. این نشان می‌دهد که درخت تولید شده در داده‌های آموزشی دچار بیش برازش شده است. به عبارت دیگر، این درختی است که مجموعه آموزشی اصلی را به‌خوبی طبقه‌بندی می‌کند، اما ساختار درخت به این مجموعه آموزشی خاص حساس است، به طوری که عملکرد آن در داده‌های جدید احتمالاً کاهش می‌یابد. اغلب می‌توان درخت ساده‌تری پیدا کرد که عملکرد بهتری نسبت به درخت پیچیده‌تر داشته باشد.

برای رفع این مشکل، درخت را هرس می‌کنیم. ابتدا خطای جایگزینی را برای زیرمجموعه‌های مختلف درخت اصلی و سپس خطای اعتبارسنجی متقابل را برای این درختان فرعی محاسبه می‌کنیم. نمودار نشان می‌دهد که خطای جایگزینی مجدد بیش از حد خوش‌بینانه است. خطای جایگزینی مجدد همیشه با رشد اندازه درخت کاهش می‌یابد، اما بعد از یک نقطه خاص، افزایش اندازه درخت، باعث افزایش نرخ خطای اعتبارسنجی متقابل می‌شود.

1resubcost = resubLoss(t,'Subtrees','all');
2[cost,secost,ntermnodes,bestlevel] = cvloss(t,'Subtrees','all');
3plot(ntermnodes,cost,'b-', ntermnodes,resubcost,'r--')
4figure(gcf);
5xlabel('Number of terminal nodes');
6ylabel('Cost (misclassification error)')
7legend('Cross-validation','Resubstitution')

خروجی به صورت زیر است.

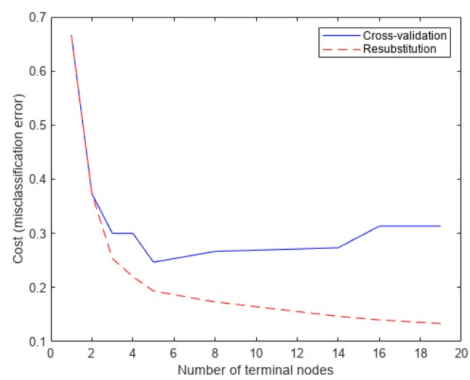
اما کدام درخت را باید انتخاب کرد؟ یک قانون ساده این است که درختی را انتخاب کنیم که کوچکترین خطای اعتبارسنجی متقابل را دارد. راه دیگر این است که از یک درخت ساده‌تر استفاده کنیم، به شرطی که تقریباً به‌خوبی درخت پیچیده‌تر باشد. در این مثال، ساده‌ترین درخت را در نظر می‌گیریم که دارای خطای استاندارد حداقلی باشد. این قانون به صورت پیش‌فرض در متد cvloss  در ClassificationTree  برقرار است.

حداقل هزینه به اضافه یک خطای استاندارد را به عنوان یک آستانه در نظر می‌گیریم و آن را در نمودار نشان می‌دهیم. «بهترین» مقدار محاسبه شده با روش cvloss برابر با کوچک‌ترین درخت، در زیر این آستانه قرار دارد. (توجه داشته باشید که bestlevel=0 مربوط به درخت هرس نشده است، بنابراین در خروجی‌های برداری از cvloss ، برای استفاده از bestlevel، آن را باید به اضافه 1 کنیم).

1[mincost,minloc] = min(cost);
2cutoff = mincost + secost(minloc);
3hold on
4plot([0 20], [cutoff cutoff], 'k:')
5plot(ntermnodes(bestlevel+1), cost(bestlevel+1), 'mo')
6legend('Cross-validation','Resubstitution','Min + 1 std. err.','Best choice')
7hold off

با توجه به کد فوق، نمودار هزینه به ازا گره‌های پایانی به شکل زیر خواهد بود.

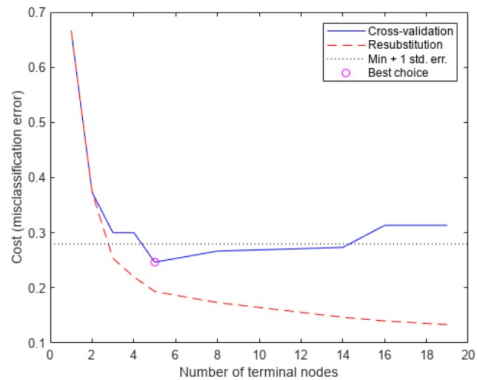
در نهایت، نمودار درخت هرس شده را ترسیم می‌کنیم و خطای تخمین طبقه‌بندی اشتباه را برای آن محاسبه می‌کنیم.

1pt = prune(t,'Level',bestlevel);
2view(pt,'Mode','graph')

با توجه به کد فوق، نمودار درخت هرس شده به شکل زیر خواهد بود.

1cost(bestlevel+1)

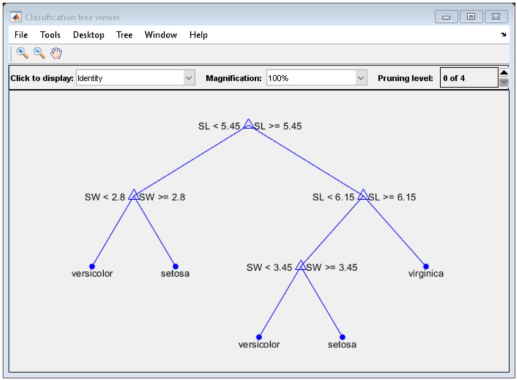
خروجی به صورت زیر خواهد بود:

ans = 0.2467

 در مثال بالا نحوه انجام طبقه‌بندی در MATLAB با استفاده از توابع موجود در جعبه ابزارهای Statistics و Machine Learning شرح داده شد. حال در ادامه به بحث آموزش هوش مصنوعی در متلب برای خوشه بندی پرداخته‌ایم.

آموزش هوش مصنوعی در متلب برای خوشه بندی

در این قسمت از آموزش هوش مصنوعی در متلب، ابتدا مروری داریم بر الگوریتم‌های خوشه‌بندی و امکاناتی که متلب در این خصوص فراهم کرده است و سپس با ارائه مثال به پیاده‌سازی برخی از این الگوریتم‌ها در محیط کدنویسی متلب خواهیم پرداخت.

الگوریتم های خوشه بندی و امکانات متلب برای آن

الگوریتم های خوشه بندی و امکانات متلب برای آن در ادامه فهرست شده‌اند.

فیلم آموزش شبکه عصبی پرسپترون + پیاده سازی در متلب

کلیک کنید

• «خوشه بندی سلسله مراتبی» (Hierarchical Clustering)
• k-Means و k-Medoids
• خوشه بندی فضایی مبتنی بر چگالی با نویز (DBSCAN)
• «خوشه‌بندی طیفی» (Spectral Clustering)
• «مدل‌های مخلوط گاوسی» (Gaussian Mixture Models)
• «نزدیکترین همسایه‌ها» (Nearest Neighbors)
• «مدل‌های پنهان مارکوف» (Hidden Markov Models)
• «تشخیص ناهنجاری» (Anomaly Detection)
• «مصور‌سازی و ارزیابی خوشه‌ها» (Cluster Visualization and Evaluation)

حال در ادامه مجموعه داده‌‌‌های زنبق یا همان آیریس را در نظر می‌گیریم و عمل خوشه‌بندی را به کمک برخی از الگوریتم‌های نام برده شده، در محیط متلب بر روی این دیتاست پیاده‌سازی می‌کنیم. الگوریتم‌های به‌کار رفته در این مثال شامل «خوشه‌بندی k-means» و «خوشه‌بندی سلسله‌مراتبی» (Hierarchical Clustering) می‌شوند.

خوشه بندی K-means چیست ؟

یک روش پارتیشن‌بندی یا همان گروه‌بندی است که مشاهدات در داده‌ها را به عنوان اشیایی در نظر می‌گیرد که دارای مکان و فاصله از یکدیگر هستند. در این روش، اشیاء به K خوشه تقسیم می‌شوند، به طوری که خوشه‌ها ۲ به ۲ از هم مجزا باشند. اشیاء درون هر خوشه تا حد امکان به یکدیگر نزدیک و اشیا در خوشه‌های مختلف تا حد امکان از یکدیگر دور هستند. هر خوشه با مرکز یا نقطه مرکزی خود مشخص می‌شود. توجه داشته باشید که فواصل مورد استفاده در خوشه‌بندی، نشان‌دهنده فواصل مکانی نیستند.

خوشه بندی سلسله مراتبی چیست ؟

روشی برای گروه‌بندی داده‌ها با مقیاس‌های مختلف فاصله‌ای است که با ایجاد یک درخت خوشه‌ای توسعه می‌یابد. در اینجا، درخت مجموعه‌ای واحد از خوشه‌ها نیست، بلکه سلسله مراتب چند سطحی است که در آن خوشه‌ها در یک سطح، در سطح بالاتر به عنوان خوشه بعدی به هم می‌پیوندند. این ویژگی به شما امکان می‌دهد تصمیم بگیرید که چه مقیاس یا سطحی از خوشه‌بندی در برنامه شما مناسب‌تر است. برخی از توابع استفاده شده در این مثال، توابع تولید اعداد تصادفی موجود در MATLAB هستند.

1rng(6,'twister')

مجموعه داده گل زنبق برای آموزش هوش مصنوعی در متلب

همانطور که در مثال طبقه‌بندی توضیح دادیم، داده‌های گل «زنبق» (Iris) یک مجموعه داده شناخته شده است که در آموزش هوش مصنوعی در متلب، پایتون و دیگر ابزارهای تحلیل هوش مصنوعی مورد استفاده قرار می‌گیرد. این داده‌ها شامل چهار ویژگی طول کاسبرگ، عرض کاسبرگ، طول گلبرگ و عرض گلبرگ برای 150 نمونه گل زنبق است. از قبل می‌دانیم که این مجموعه سه دسته از انواع زنبق را شامل می‌شود و هر دسته شامل 50 نمونه است.

آموزش هوش مصنوعی در متلب برای خوشه بندی K-Means

تابع kmeans  خوشه‌بندی K-Means را با استفاده از یک الگوریتم تکرار شونده انجام می‌دهد، به طوری که در هر خوشه، مجموع فواصل هر شی تا مرکز آن خوشه‌، حداقل باشد. با استفاده از داده‌های گل زنبق، گروه‌بندی‌های طبیعی را در بین نمونه‌ها بر اساس اندازه‌ کاسبرگ و گلبرگ‌ پیدا می‌کنیم.

ابتدا داده‌ها را بارگذاری می‌کنیم، در الگوریتم K-Means قبل از هر چیزی باید تعداد خوشه‌ها را مشخص کرد. ما در اینجا k را برابر با 2 در نظر می‌گیریم و تنظیمات مربوط به فاصله را از نوع اقلیدسی قرار می‌دهیم. برای این که متوجه شویم خوشه‌ها چقدر خوب از هم جدا شده‌اند، می‌توانیم نمودار «سیلوئت» (Silhouette) را ترسیم کنیم که نشان‌دهنده میزان نزدیکی هر یک از نقاط در یک خوشه به نقاط در خوشه‌های همسایه است.

1load fisheriris
2[cidx2,cmeans2] = kmeans(meas,2,'dist','sqeuclidean');
3[silh2,h] = silhouette(meas,cidx2,'sqeuclidean');

با توجه به کدفوق، نمودار سیلوئت به شکل زیر خواهد بود.

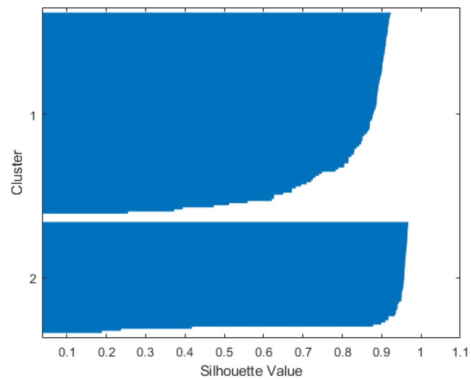
در نمودار Silhouette، می‌توانید ببینید که بیشتر نقاط در هر دو خوشه دارای مقدار سیلوئت بزرگتر از 0.8 هستند (که رقم نسبتاً بزرگی به حساب می‌آید). این نشان می‌دهد نقاط به‌خوبی از خوشه‌های همسایه جدا شده‌اند. با این حال، هر خوشه همچنین حاوی چند نقطه با مقادیر سیلوئت کم است، که نشان می‌دهد این نقاط در نزدیکی نقاط خوشه‌های دیگر هستند.

به نظر می‌رسد که چهارمین ویژگی در این داده‌ها که عرض گلبرگ است، با ویژگی سوم، یعنی طول گلبرگ، «همبستگی» (Corelation) زیادی دارد و بنابراین نمودار سه بُعدی با استفاده از ۳ ویژگی اول و با صرف نظر کردن از ویژگی چهارم، داده‌ها را به‌خوبی نمایش خواهد داد. با ترسیم داده‌ها با شکل‌های سمبولیک می‌توان داده‌‌ها با مقدار سیلوئت کوچک و نزدیک به دیگر خوشه‌ها را شناسایی کرد.

1ptsymb = {'bs','r^','md','go','c+'};
2for i = 1:2
3clust = find(cidx2==i);
4plot3(meas(clust,1),meas(clust,2),meas(clust,3),ptsymb{i});
5hold on
6end
7plot3(cmeans2(:,1),cmeans2(:,2),cmeans2(:,3),'ko');
8plot3(cmeans2(:,1),cmeans2(:,2),cmeans2(:,3),'kx');
9hold off
10xlabel('Sepal Length');
11ylabel('Sepal Width');
12zlabel('Petal Length');
13view(-137,10);
14grid on

با توجه به کد فوق، نمودار پراکندگی به شکل زیر خواهد بود.

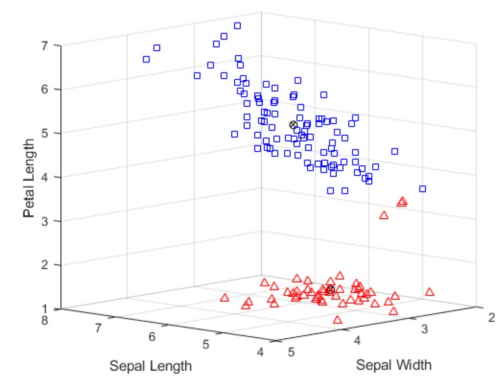
مرکز هر خوشه با استفاده از علامت دایره‌ حاوی دو قطر ضربدری نشان داده شده است. سه نقطه از خوشه پایینی (نقاط مثلثی) به نقاط خوشه بالایی (نقاط مربعی) بسیار نزدیک هستند. در خوشه پایینی این سه نقطه با یک شکاف از بخش عمده‌ای از نقاط خوشه خود جدا شده‌اند اما با این وجود، به علت گستردگی خوشه بالایی، آن سه نقطه نسبت به مرکز خوشه پایینی نزدیکتر هستند. این نتیجه از آنجایی نشأت می‌گیرد که خوشه‌بندی K-Means فقط فواصل و نه چگالی را در نظر می‌گیرد.

می‌توانیم تعداد خوشه‌ها را افزایش دهیم تا ببینیم آیا k-means می‌تواند ساختار گروه‌بندی بیشتری را در داده‌ها پیدا کند یا خیر؛ این بار برای چاپ اطلاعات مربوط به هر تکرار در الگوریتم خوشه‌بندی از آرگومان‌های «Display» و «iter» استفاده می‌کنیم.

1[cidx3,cmeans3] = kmeans(meas,3,'Display','iter');

با اجرای کد بالا، در خروجی آمار مربوط به تکرارها در الگوریتم k-means را ملاحظه می‌کنیم که به صورت زیر خواهد بود.

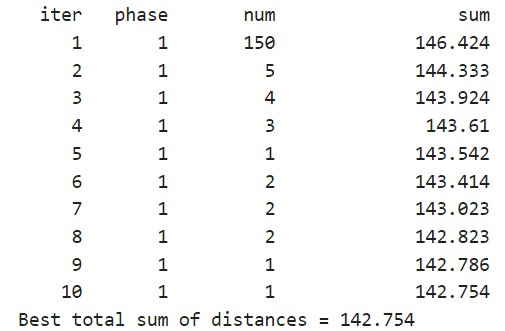
در هر تکرار، الگوریتم k-means نقاط را بین خوشه‌ها مجدداً اختصاص می‌دهد تا مجموع فواصل نقاط تا مرکز را کاهش دهد و سپس مرکزهای خوشه‌ای جدید را دوباره محاسبه می‌کند. توجه داشته باشید که مجموع کل فاصله‌ها و تعداد تخصیص مجدد در هر تکرار کاهش می‌یابد، تا زمانی که این مقادیر در الگوریتم به یک سطح حداقلی برسند. الگوریتم مورد استفاده در k-means از دو فاز تشکیل شده است. در مثال اینجا در فاز دوم الگوریتم، هیچ گونه تخصیص مجددی انجام نشده است که نشان می‌دهد در فاز اول تنها پس از چند بار، مقادیر به حداقل رسیده‌اند.

به طور پیش‌فرض، k-means فرآیند خوشه‌بندی را با استفاده از مجموعه‌ای از مکان‌های مرکزی اولیه آغاز می‌کند که به طور تصادفی انتخاب شده‌اند. الگوریتم kmeans می‌تواند به یک راه حل همگرا شود که به صورت محلی کمینه است. یعنی این احتمال وجود دارد kmeans داده‌ها را به گونه‌ای تقسیم‌بندی کند که انتقال هر نقطه به یک خوشه دیگر مجموع فاصله‌ها را افزایش دهد. راه حلی که kmeans ارائه می‌دهد، مانند بسیاری از انواع دیگر کمینه‌سازی‌های عددی، گاهی به نقاط شروع بستگی دارد.

بنابراین ممکن است راه‌حل‌ها یا مینیمم‌های محلی دیگری که مجموع فاصله‌های کمتری دارند نیز وجود داشته باشند. می‌توانیم از آرگومان اختیاری «Replicates» برای تست راه‌حل‌های مختلف استفاده کنیم. هنگامی که بیش از یک تکرار را مشخص می‌کنیم، kmeans فرآیند خوشه‌بندی را با شروع از مراکز مختلف منتخب تصادفی در هر Replicate تکرار می‌کند. سپس kmeans با توجه به همه تکرارها و از بین مقادیر مربوط به مجموع کل فاصله‌ها، راه‌حل با کم‌ترین مقدار را برمی‌گرداند.

1[cidx3,cmeans3,sumd3] = kmeans(meas,3,'replicates',5,'display','final');

با اجرای کدفوق، مجموع فواصل در هر تکرار، به صورت زیر، قابل مشاهده خواهد بود.

خروجی نشان می‌دهد که حتی در این مسئله نسبتاً ساده، برخی «مینیمم‌های محلی» (Non-Global Minima) وجود دارند. هر یک از این پنج تکرار از مجموعه متفاوتی از مراکز اولیه آغاز شده‌اند. راه‌حل نهایی که kmeans برمی‌گرداند، راه‌حلی است که کمترین مجموع فاصله‌ها را در تمام تکرارها دارد. آرگومان خروجی سوم نشان‌دهنده مجموع فواصل درون هر خوشه برای بهترین راه‌حل است.

1sum(sumd3)

جواب برابر با 78.8514 می‌شود. نمودار سیلوئت برای این راه‌حل سه خوشه‌ای نشان می‌دهد که یکی از خوشه‌ها به‌خوبی از دو خوشه دیگر جدا شده است، اما دو خوشه دیگر خیلی متمایز نیستند.

1[silh3,h] = silhouette(meas,cidx3,'sqeuclidean');

خروجی کد فوق، برای نمایش سیلوئت به شکل زیر خواهد بود.

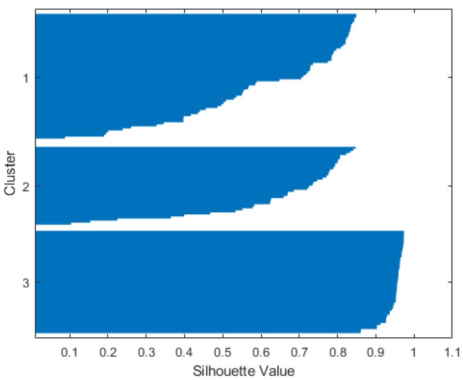
دوباره داده‌های خام را رسم می‌کنیم تا ببینیم k-means چگونه نقاط را به خوشه‌ها تخصیص داده است.

1for i = 1:3
2clust = find(cidx3==i);
3plot3(meas(clust,1),meas(clust,2),meas(clust,3),ptsymb{i});
4hold on
5end
6plot3(cmeans3(:,1),cmeans3(:,2),cmeans3(:,3),'ko');
7plot3(cmeans3(:,1),cmeans3(:,2),cmeans3(:,3),'kx');
8hold off
9xlabel('Sepal Length');
10ylabel('Sepal Width');
11zlabel('Petal Length');
12view(-137,10);
13grid on[silh3,

با اجرا کردن قطعه کد بالا، نمودار پراکندگی خوشه‌بندی را به شکل زیر ملاحظه می‌کنیم.

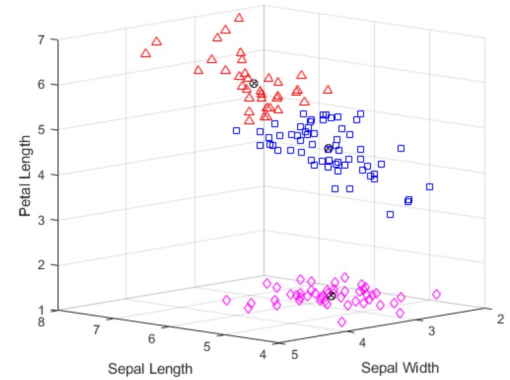
می‌بینیم که kmeans خوشه بالایی را از راه حل دو خوشه‌ای جدا کرده است اما این دو خوشه بسیار به هم نزدیک هستند. بسته به این که پس از خوشه‌بندی قصد داریم چه کاری انجام دهیم، این راه حل سه خوشه‌ای می‌تواند کم و بیش از راه‌حل دو خوشه‌ای مفیدتر باشد. اولین آرگومان خروجی در silhouette  حاوی مقادیر silhouette برای هر نقطه است که می‌توانیم از آن‌ها برای مقایسه کمی دو راه‌حل استفاده کنیم. میانگین مقدار سیلوئت برای راه‌حل دو خوشه‌ای بزرگتر است، که نشان می‌دهد که این پاسخ صرفاً از نقطه نظر ایجاد خوشه‌های متمایز پاسخ بهتری است.

1[mean(silh2) mean(silh3)]

اجرای کد فوق، میانگین مقادیر سیلوئت را به صورت زیر برمی‌گرداند.

همچنین می‌توانیم داده‌ها را با استفاده از معیار و فاصله متفاوتی خوشه‌بندی کنیم. فاصله کسینوسی یکی از معیارهایی است که ممکن است برای این داده‌ها منطقی باشد زیرا اندازه‌های مطلق مقادیر در این روش نادیده گرفته می‌شود و فقط اندازه‌های نسبی آن‌ها منظور می‌شود. بنابراین، دو گل با اندازه‌های متفاوت، اما گلبرگ‌ها و کاسبرگ‌های مشابه، ممکن است از نظر فاصله اقلیدسی نزدیک هم محسوب نشوند، اما از نظر فاصله کسینوسی نزدیک یکدیگر باشند.

1[cidxCos,cmeansCos] = kmeans(meas,3,'dist','cos');

از نمودار سیلوئت، به نظر می‌رسد که این خوشه‌ها فقط کمی بهتر از خوشه‌هایی هستند که با استفاده از فاصله اقلیدسی به دست می‌آیند.

1[silhCos,h] = silhouette(meas,cidxCos,'cos');
2[mean(silh2) mean(silh3) mean(silhCos)]

اجرای کد فوق، میانگین مقادیر سلوئت را به صورت زیر برمی‌گرداند.

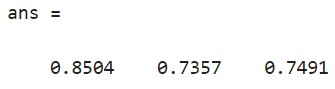
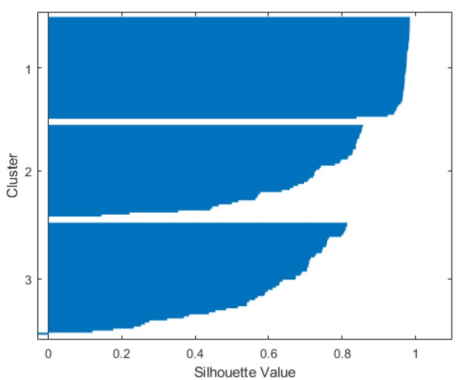
توجه داشته باشید که ترتیب خوشه‌ها در مقایسه با نمودار سیلوئت قبلی متفاوت است. این تفاوت به این دلیل است که kmeans انتساب‌های اولیه خوشه را به صورت تصادفی انتخاب می‌کند. با ترسیم داده‌های خام، می‌توانیم تفاوت در اشکال خوشه‌ای ایجاد شده با استفاده از دو فاصله متفاوت را مشاهده کنیم. این دو راه حل شبیه به هم هستند، اما در هنگام استفاده از فاصله کسینوسی، دو خوشه بالایی در جهت مبدا کشیده می‌شوند.

1for i = 1:3
2clust = find(cidxCos==i);
3plot3(meas(clust,1),meas(clust,2),meas(clust,3),ptsymb{i});
4hold on
5end
6hold off
7xlabel('Sepal Length');
8ylabel('Sepal Width');
9zlabel('Petal Length');
10view(-137,10);
11grid on

نمودار پراکندگی خوشه‌‌بندی در خروجی کد به این شکل خواهد بود.

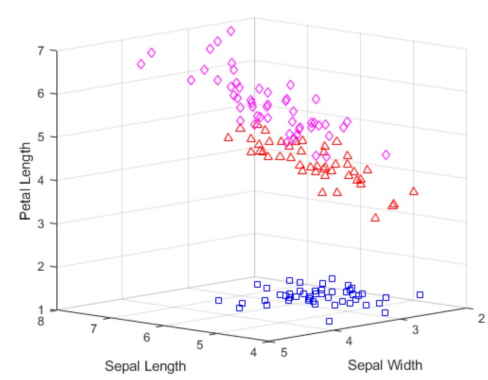
این نمودار مراکز خوشه را نمایش نمی‌دهد، زیرا در فاصله کسینوسی، مرکز با یک نیم خط از مبدا نمایش داده می‌شود. با این حال، می‌توان از نقاط داده نرمال شده یک نمودار مختصات موازی برای مصورسازی تفاوت بین مراکز خوشه ترسیم کرد.

1lnsymb = {'b-','r-','m-'};
2names = {'SL','SW','PL','PW'};
3meas0 = meas ./ repmat(sqrt(sum(meas.^2,2)),1,4);
4ymin = min(min(meas0));
5ymax = max(max(meas0));
6for i = 1:3
7subplot(1,3,i);
8plot(meas0(cidxCos==i,:)',lnsymb{i});
9hold on;
10plot(cmeansCos(i,:)','k-','LineWidth',2);
11hold off;
12title(sprintf('Cluster %d',i));
13xlim([.9, 4.1]);
14ylim([ymin, ymax]);
15h_gca = gca;
16h_gca.XTick = 1:4;
17h_gca.XTickLabel = names;
18endfor i = 1:3

با اجرای کد فوق، نمودار مختصات موازی برای نمایش تفاوت بین مراکز خوشه ها به این صورت ترسیم خواهد شد.

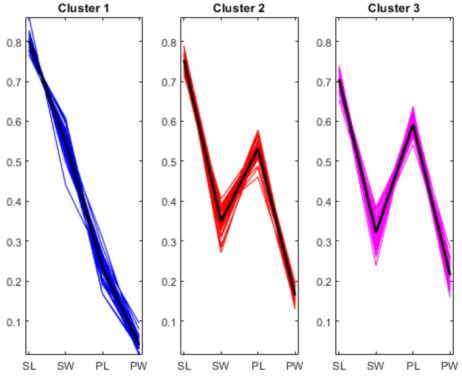
از نمودارهای بالا مشخص است که نمونه‌های هر یک از سه خوشه به طور متوسط اندازه‌های نسبی متفاوتی از گلبرگ‌ها و کاسبرگ‌ها دارند. اولین خوشه دارای گلبرگ‌هایی است که کاملاً کوچکتر از کاسبرگ‌ها هستند. گلبرگ‌ها و کاسبرگ‌های دو خوشه دوم از نظر اندازه با هم هم‌پوشانی دارند. این هم‌پوشانی در خوشه سوم بیشتر از دسته دوم است. علاوه بر این خوشه‌های دوم و سوم شامل نمونه‌هایی هستند که بسیار شبیه به یکدیگرند.

از آنجایی که ما از انواع گونه‌های هر مشاهده در داده‌ها اطلاع داریم، می‌توانیم خوشه‌های به دست آمده توسط k-means را با گونه‌های واقعی مقایسه کنیم تا ببینیم آیا این سه گونه ویژگی‌های فیزیکی متفاوتی دارند یا خیر. در واقع، همانطور که نمودار زیر نشان می‌دهد، خوشه‌های ایجاد شده با استفاده از فاصله کسینوسی با گروه‌های گونه گل زنبق تنها برای پنج گل متفاوت است. آن پنج نقطه که به شکل ستاره‌ای و با رنگ سیاه ترسیم شده‌اند، همگی نزدیک مرز دو خوشه بالایی قرار دارند.

1subplot(1,1,1);
2for i = 1:3
3clust = find(cidxCos==i);
4plot3(meas(clust,1),meas(clust,2),meas(clust,3),ptsymb{i});
5hold on
6end
7xlabel('Sepal Length');
8ylabel('Sepal Width');
9zlabel('Petal Length');
10view(-137,10);
11grid on
12sidx = grp2idx(species);
13miss = find(cidxCos ~= sidx);
14plot3(meas(miss,1),meas(miss,2),meas(miss,3),'k*');
15legend({'setosa','versicolor','virginica'});
16hold off

نمودار پراکندگی خوشه‌بندی با اجرای کد فوق به شکل زیر ترسیم خواهد شد.

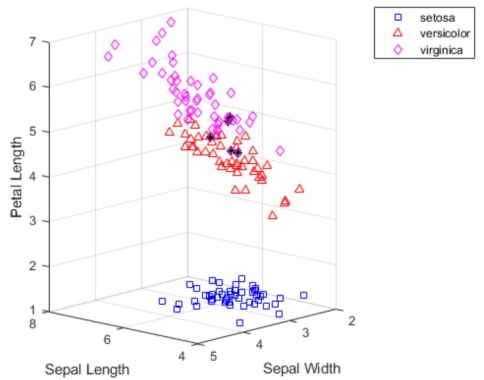
آموزش هوش مصنوعی در متلب برای خوشه بندی سلسله مراتبی

در ادامه آموزش هوش مصنوعی در متلب، در این بخش به خوشه‌بندی سلسله مراتبی می‌پردازیم. داده‌های مورد استفاده در این مثال نیز همانند مثال‌های حل شده در بالا، شامل «مجموعه داده گل‌های زنبق» (Iris Dataset) است. خوشه‌بندی K-Means داده‌های آیریس را «افراز» (Partition) می‌کند. اما اگر بخواهیم مقیاس‌های مختلف گروه‌بندی را نیز در داده‌ها بررسی کنیم، خوشه‌بندی سلسله مراتبی به ما این امکان را می‌دهد که این کار را با ایجاد یک درخت سلسله مراتبی از خوشه‌ها انجام دهیم.

ابتدا یک درخت خوشه‌بندی با استفاده از فواصل بین مشاهدات و با استفاده از معیار فاصله اقلیدسی در داده‌ها ایجاد می‌کنیم.

1eucD = pdist(meas,'euclidean');
2clustTreeEuc = linkage(eucD,'average');

همبستگی «کوفنه‌تیک» (Cophenetic) یکی از راه‌های بررسی سازگاری درخت خوشه‌بندی با فواصل اصلی است. مقادیر بزرگ نشان می‌دهد که درخت به‌خوبی با فواصل مطابقت دارد، به این معنا که پیوندهای زوجی بین مشاهدات با فواصل زوجی واقعی آنها همبستگی دارند. به نظر می‌رسد این درخت با فاصله‌ها برازش خوبی دارد.

1cophenet(clustTreeEuc,eucD)

جواب برابر با 0.8770 است. برای مصورسازی خوشه‌بندی سلسه‌مراتبی می‌توانیم از دندوگرام‌ استفاده کنیم.

1[h,nodes] = dendrogram(clustTreeEuc,0);
2h_gca = gca;
3h_gca.TickDir = 'out';
4h_gca.TickLength = [.002 0];
5h_gca.XTickLabel = [];

خروجی کد فوق، دندوگرام را به شکل زیر ترسم خواهد کرد.

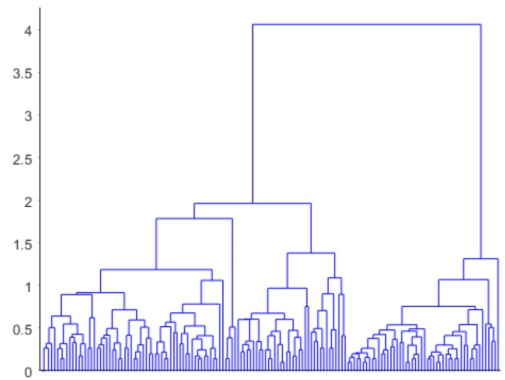
گره ریشه در این درخت بسیار بالاتر از دیگر گره‌ها است. این موضوع نشان‌دهنده دو گروه بزرگ و متمایز از مشاهدات و همسو و تایید کننده نتایج به دست آمده از خوشه‌بندی k-means است. در هر یک از این دو گروه، با کوچک‌تر شدن مقیاس فاصله، می‌توانیم ببینیم که سطوح پایین‌تری از گروه‌ها ظاهر می‌شوند. این سطوح مختلف، نشان‌دهنده گروه‌ها با اندازه‌ها و با درجه تمایز مختلف هستند.

بر اساس نتایج حاصل از خوشه‌بندی K-Means، معیار کسینوسی راه‌حل خوبی برای اندازه‌گیری فاصله‌ها است. معیار کسینوسی در درخت سلسله مراتبی به دست آمده کاملاً متفاوت است و راه بسیار متفاوتی را برای نگاه کردن به ساختار گروه‌بندی داده‌ها پیشنهاد می‌کند.

1cosD = pdist(meas,'cosine');
2clustTreeCos = linkage(cosD,'average');
3cophenet(clustTreeCos,cosD)

جواب برابر با 0.9360 است.

1[h,nodes] = dendrogram(clustTreeCos,0);
2h_gca = gca;
3h_gca.TickDir = 'out';
4h_gca.TickLength = [.002 0];
5h_gca.XTickLabel = [];

ترسیم دندوگرام با لحاظ معیار کسینوسی به شکل زیر است که ملاحظه می‌کنید.

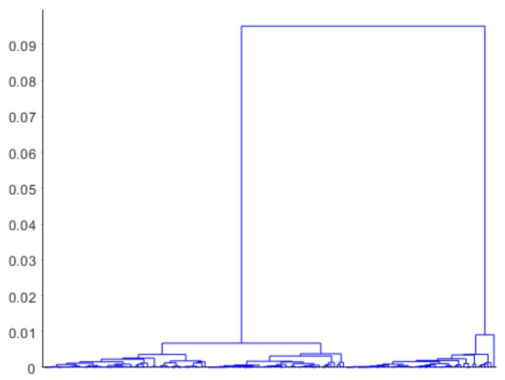
در بالاترین سطح این درخت، نمونه‌های گل زنبق به دو گروه کاملاً متمایز تقسیم می‌شوند. مقایسه دو نمودار دندروگرام با فاصله‌های اقلیدسی و کسینوسی، نشان می‌دهد تفاوت‌های درون گروهی نسبت به تفاوت‌های بین گروهی در حالت دوم بسیار کمتر است. این اتفاق دور از انتظار نیست، زیرا فاصله کسینوسی یک فاصله زوجی صفر را برای اجسامی که در «جهت» یکسان از مبدا قرار دارند محاسبه می‌کند. نمودار دندوگرام برای 150 مشاهده، به هم ریخته است، اما می‌توانیم دندروگرام ساده‌تری ترسیم کنیم که پایین‌ترین سطوح درخت را شامل نمی‌شود.

1[h,nodes] = dendrogram(clustTreeCos,12);

ترسیم زیر حالت ساده‌سازی شده‌ی دندوگرام اخیر است که با اجرای کد فوق در خروجی دریافت خواهیم کرد.

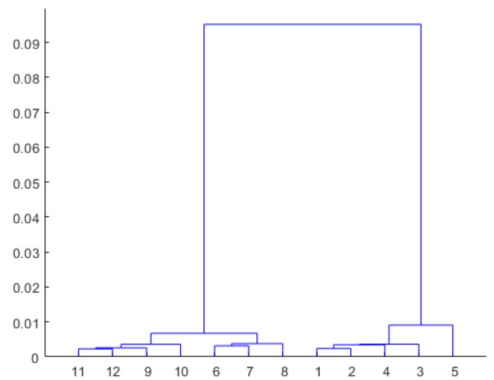
سه گره بالاتر در این درخت، سه گروه با اندازه مساوی را به اضافه یک نوع واحد از گونه‌های گل (با برچسب گره برگ 5) که نزدیک هیچ گروه دیگری نیست، جدا می‌کنند.

1[sum(ismember(nodes,[11 12 9 10])) sum(ismember(nodes,[6 7 8])) ...
2sum(ismember(nodes,[1 2 4 3])) sum(nodes==5)]

خروجی کدهای فوق به صورت زیر خواهد بود:

ans =

54 46 49 1

 برای بسیاری از اهداف، دندروگرام ممکن است یک نتیجه کافی به حساب بیاید. با این حال، می‌توانیم یک مرحله پیش برویم و از تابع cluster  برای برش درخت و تقسیم مشاهدات به خوشه‌ها استفاده کنیم. برای پیاده‌سازی خوشه‌بندی سلسله مراتبی با فاصله کسینوسی، «ارتفاع پیوند» (Linkage Height) را مشخص می‌کنیم که درخت را از زیر سه گره بالاتر بریده و چهار خوشه ایجاد می‌کند، سپس داده‌های خام خوشه‌بندی را رسم می‌کند.

1hidx = cluster(clustTreeCos,'criterion','distance','cutoff',.006);
2for i = 1:5
3clust = find(hidx==i);
4plot3(meas(clust,1),meas(clust,2),meas(clust,3),ptsymb{i});
5hold on
6end
7hold off
8xlabel('Sepal Length');
9ylabel('Sepal Width');
10zlabel('Petal Length');
11view(-137,10);
12grid on

خروجی کد فوق برای ترسیم نمودار پراکندگی خوشه‌بندی به شکل زیر است.

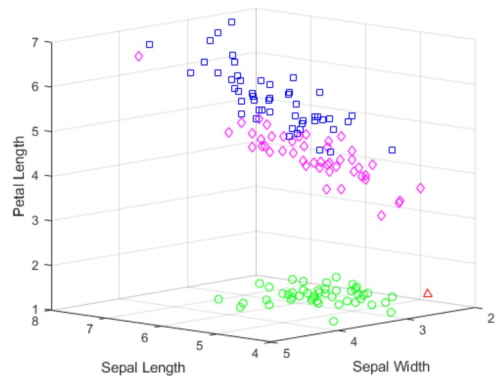
این نمودار نشان می‌دهد که نتایج حاصل از خوشه‌بندی سلسله مراتبی با فاصله کسینوسی از نظر کیفی مشابه نتایج K-Means با احتساب سه خوشه است. ایجاد یک درخت خوشه‌بندی سلسله‌مراتبی برخی مزایا را به همراه دارد. در خوشه‌بندی k-means نیاز به آزمایش‌های قابل توجه با مقادیر مختلف K وجود دارد که با مصورسازی نمودار درختی دندوگرام می‌توان به طور همزمان این موضوع را تسهیل کرد.

خوشه‌بندی سلسله مراتبی همچنین به ما امکان می‌دهد تا با پیوندهای مختلف آزمایش کنیم. برای مثال، خوشه‌بندی داده‌های گل زنبق با «پیوند منفرد» (Single Linkage) که تمایل دارد اشیاء را در فواصل بزرگ‌تر از فاصله متوسط به هم پیوند دهد، تفسیر بسیار متفاوتی از ساختار داده‌ها دارد.

1clustTreeSng = linkage(eucD,'single');
2[h,nodes] = dendrogram(clustTreeSng,0);
3h_gca = gca;
4h_gca.TickDir = 'out';
5h_gca.TickLength = [.002 0];
6h_gca.XTickLabel = [];

ترسیم دندوگرام با پیوند منفرد در خروجی کد فوق، به شکل زیر است.

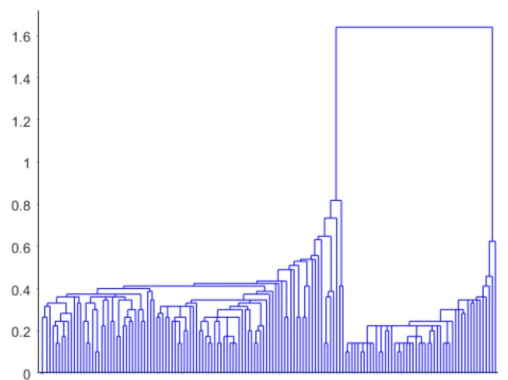
آموزش هوش مصنوعی در متلب با استفاده از الگوریتم ژنتیک

در این بخش از آموزش هوش مصنوعی در متلب، مثالی برای شرح و پیاده‌سازی الگوریتم ژنتیک ارائه شده است. این مثال نشان می‌دهد که چگونه می‌توان می‌نیمم یک تابع هدف را با استفاده از الگوریتم ژنتیک پیدا کرد.

مسئله بهینه سازی مقید در متلب

در این مسئله، تابع هدفی که قصد داریم آن را کمینه سازیم، یک تابع ساده شامل متغیر درجه دوم x است.

1simple_objective(x) = (4 - 2.1*x(1)^2 + x(1)^4/3)*x(1)^2 + x(1)*x(2) + (-4 + 4*x(2)^2)*x(2)^2;

مرزها و قیدهای غیرخطی در این مسئله شامل موارد زیر می‌شود.

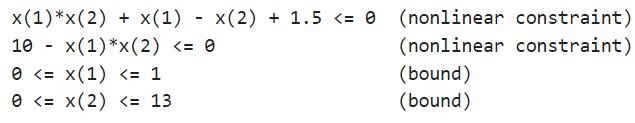
توسعه کد برای تابع برازش در متلب

یک فایل متلب با نام simple_objective.m حاوی کد زیر ایجاد می‌کنیم.

1type simple_objective

با اجرای کد فوق، خروجی‌های زیر را خواهیم داشت.

ga یک ورودی به نام x را می‌پذیرد، که در آن عناصر x برابر با اندازه تعداد متغیرهای مسئله است. تابع هدف، مقدار اسکالر تابع هدف را محاسبه می‌کند و آن را در آرگومان خروجی y برمی‌گرداند.

توسعه کد برای تابع قید در متلب

یک فایل متلب با نام simple_constraint.m حاوی کد زیر ایجاد می‌کنیم.

1type simple_constraint

با اجرای کد قید مسئله، خروجی‌های زیر را خواهیم داشت.

تابع قید مقادیر تمام قیود نابرابری و برابری را محاسبه می‌کند و به ترتیب بردارهای c و ceq را برمی‌گرداند. مقدار c نشان‌دهنده قیدهای نابرابری غیرخطی است که حل‌کننده سعی می‌کند آن را برابر با و یا کمتر از صفر سازد. مقدار ceq قیود برابری غیرخطی را نشان می‌دهد که حل‌کننده سعی می‌کند آن‌ها را برابر با صفر قرار دهد. این مثال هیچ قید تساوی غیرخطی ندارد، بنابراین [] = ceq خواهد بود.

کمینه سازی با استفاده از الگوریتم ژنتیک در متلب

تابع هدف را به صورت یک function handle مشخص می‌کنیم.

1ObjectiveFunction = @simple_objective;

مرزهای مسئله را مشخص می‌کنیم.

1ConstraintFunction = @simple_constraint;

تعداد متغیرهای مسئله را مشخص می‌کنیم.

1nvars = 2;

حل کننده را فراخوانی می‌کنیم و در آن نقطه بهینه x و مقدار تابع در نقطه بهینه fval را درخواست می‌کنیم.

1rng default % For reproducibility
2[x,fval] = ga(ObjectiveFunction,nvars,[],[],[],[],lb,ub,ConstraintFunction)

با اجرای کد فوق، در خروجی مقادیر x و fval را ملاحظه می‌کنیم.

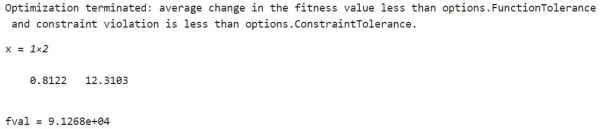
مصورسازی

برای مشاهده پیشرفت حل‌کننده، دو تابع نمودار را انتخاب می‌کنیم. تابع نمودار gaplotbestf  بهترین مقدار تابع هدف را در هر تکرار ترسیم می‌کند و تابع نمودار gaplotmaxconstr  حداکثر تخطی از قید را در هر تکرار ترسیم می‌کند. این دو تابع مربوط به ترسیم نمودار را در یک «آرایه سلولی» (Cell Array) تنظیم می‌کنیم. همچنین، با تنظیم گزینه Display بر روی 'iter'، اطلاعات مربوط به پیشرفت حل‌کننده را در Command Window نمایش می‌دهیم.

1[x,fval] = ga(ObjectiveFunction,nvars,[],[],[],[],lb,ub, ...
2ConstraintFunction,options)

با اجرای کد فوق، خروجی‌های زیر را خواهیم داشت.

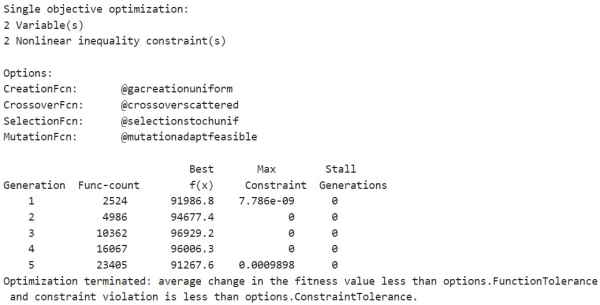
و راه‌حل بهینه و بیشینه قید بازا نسل‌های مختلف به صورت زیر قابل مشاهده است.

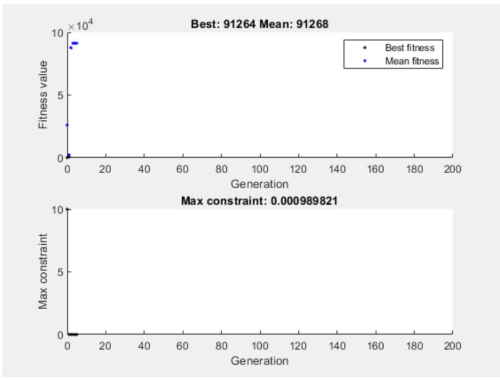
و مقادیر x و fval به صورت زیر محاسبه می‌شود.

الگوریتم ژنتیک جزئیات مربوط به نوع مسئله و عملگرهای ایجاد، متقاطع، جهش و انتخاب را در هر تکرار ارائه می‌دهد.

الگوریتم ژنتیک در مسائل با قیود غیرخطی، بسیاری از مسائل فرعی را در هر تکرار حل می‌کند. همانطور که در آمار تکرار‌ها و در نمودارها نشان داده شده است، فرآیند حل این مسئله تکرارهای کمی دارد. با این حال، ستون Func-count در نمایشگر تکرار، بسیاری از ارزیابی‌های تابع را در هر تکرار شامل می‌شود.

رویکرد ga با مرزها و قیود خطی، متفاوت از رویکرد آن با قیود غیرخطی است. تمام قیود و مرزهای خطی در طول بهینه‌سازی برآورده می‌شوند. با این حال، ga ممکن است تمام محدودیت‌های غیرخطی را در هر نسل برآورده نکند. اگر ga به یک راه‌حل همگرا شود، قیدهای غیرخطی در آن جواب برآورده شده‌اند.

ga از توابع جهش و متقاطع برای تولید افراد جدید در هر نسل استفاده می‌کند. ga قیود خطی و محدود را با استفاده از توابع جهش و متقاطع طوری برآورده می‌کند که نقاط «امکان‌پذیر» (Feasible) ایجاد شود. تابع جهش پیش‌فرض ga در مسائل غیرمقید، تابع mutationgaussian  است که قیدهای خطی را برآورده نمی‌کند و بنابراین ga به‌جای آن به طور پیش‌فرض از تابع mutationadaptfeasible  استفاده می‌کند. اگر یک تابع جهش سفارشی در دست داشته باشیم، این تابع سفارشی فقط نقاطی را می‌تواند ایجاد کند که با توجه به قیود خطی و محدود «امکان‌پذیر» (Feasible) باشد. تمام توابع متقاطع در جعبه ابزار، نقاطی را ایجاد می‌کنند که قیود و مرزهای خطی را برآورده می‌کنند.

با این حال، زمانی که مسئله شامل قیود عدد صحیح است، ga در تمامی تکرارها، قیود خطی را برآورده می‌کند. این امکان‌ در یک تلورانس کوچک، برای همه اپراتورهای ایجاد، جهش‌ و متقاطع‌ها وجود دارد.

پیشنهاد نقطه شروع

برای سرعت بخشیدن به حل کننده، می‌توانیم یک جمعیت اولیه در گزینه InitialPopulationMatrix  ارائه دهیم. ga از جمعیت اولیه برای شروع بهینه سازی خود استفاده می‌کند. یک بردار سطری یا یک ماتریس را مشخص می‌کنیم که در آن هر سطر یک نقطه شروع را نشان می‌دهد.

1X0 = [0.8 12.5]; % Start point (row vector)
2options.InitialPopulationMatrix = X0;
3[x,fval] = ga(ObjectiveFunction,nvars,[],[],[],[],lb,ub, ...
4ConstraintFunction,options)

با اجرای کد فوق، برای پیشنهاد جمعیت اولیه، خروجی‌های زیر را خواهیم داشت.

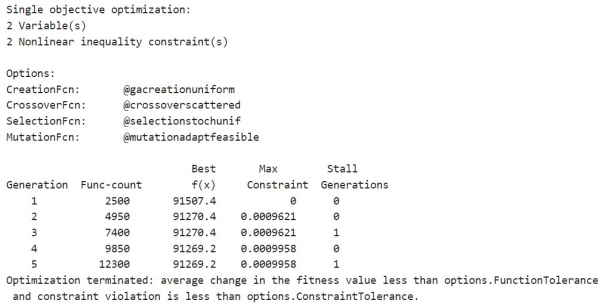
و راه‌حل بهینه و بیشینه قید بازا نسل‌های مختلف به صورت زیر محاسبه می‌شود.

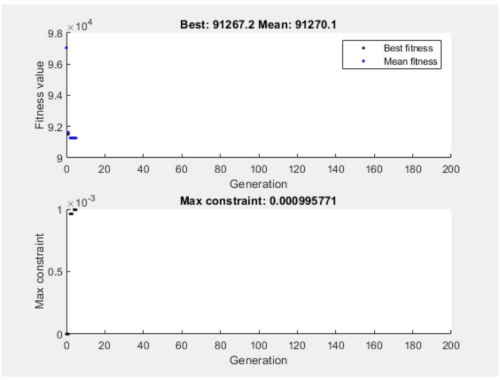
خروجی به صورت زیر محاسبه می‌شود.

x = 1×2
0.8122 12.3104
fval = 9.1269e+04

ملاحظه می‌کنیم که در این مثال، ارائه نقطه شروع به طور اساسی تغییری در پیشرفت حل کننده ایجاد نمی‌کند.

سوالات رایج و پرتکرار

در این بخش به برخی از سوالاتی پاسخ داده شده است که در آموزش هوش مصنوعی در متلب مکرراً مطرح می‌شود.

چرا متلب ابزار مناسبی برای هوش مصنوعی به حساب می‌آید؟

متلب راه‌های مختلفی برای تعامل و انتقال داده‌ها بین چارچوب‌های یادگیری عمیق دارد. MATLAB از ONNX برای ورود و خروج مدل‌ها در سایر فریم‌ورک‌ها پشتیبانی می‌کند. به عنوان مثال، یک مدل طراحی شده در PyTorch را می‌توان به MATLAB وارد کرد و مدل‌های آموزش دیده در MATLAB را می‌توان با استفاده از چارچوب ONNX خارج کرد.

MATLAB چگونه در هوش مصنوعی استفاده می شود؟

MATLAB قابلیت‌هایی مشابه ابزارهای اختصاصی هوش مصنوعی مانند Caffe و TensorFlow را ارائه می‌کند و مهم‌تر از آن، MATLAB به شما امکان می‌دهد هوش مصنوعی را در گردش کار کامل برای توسعه یک سیستم کاملاً مهندسی شده ادغام کنید. یک مدل هوش مصنوعی تنها بخشی از گردش کار کامل برای توسعه یک سیستم کاملاً مهندسی شده به حساب می‌آید.

خواستگاه متلب چیست؟

MATLAB یک پلت‌فرم برنامه‌نویسی است که به طور خاص برای مهندسان و دانشمندان طراحی شده است تا سیستم‌ها و محصولات را تجزیه و تحلیل و طراحی کنند. قلب متلب، زبان متلب است، زبانی مبتنی بر ماتریس که امکان بیان طبیعی‌ترین ریاضیات محاسباتی را فراهم می‌کند.

بیشترین کاربرد متلب در کجاست؟

برخی از مهم‌ترین کاربردهای متلب شامل موارد زیر می‌شود.

• مکاترونیک
• تست و اندازه گیری
• زیست شناسی محاسباتی و مالی محاسباتی
• رباتیک
• تجزیه و تحلیل داده‌ها
• تعمیرات قابل پیش‌بینی
• کنترل موتور و قدرت
• یادگیری عمیق

فیلم آموزش هوش مصنوعی – تکمیلی در فرادرس

کلیک کنید

جمع‌بندی

در این مقاله سعی شد به طور جامع به آموزش هوش مصنوعی در متلب پرداخته شود. انواع روش‌های با نظارت و بدون نظارت در یادگیری ماشین از جمله طبقه‌بندی، خوشه‌بندی و بسیاری از روش‌ها و الگوریتم‌های مختلف هوش مصنوعی در متلب آموزش داده و مثال‌های متعددی هم برای آن‌ها ارائه شد. همچنین دوره‌های آموزشی مختلفی هم معرفی شدند که علاقه‌مندان می‌توانند برای یادگیری بیشتر از آن‌ها استفاده کنند. امید است این نوشته مفید واقع شود.