مجموعه چیست؟ – ریاضی با مثال و به زبان ساده
احتمالاً واژه «مجموعه» را در اطرافتان بسیار شنیدهاید که اغلب به معنی تعدادی چیز در کنار هم است و برای بیان با هم بودن تعدادی چیز (هر چیزی، از مجموعه اهداف تا مجموعه محصولات، مجموعه کتابها و...) آنها را به کار بردهاید. اما در ریاضی، مجموعه چیست و چه تعریفی دارد؟ در این آموزش به پاسخ این پرسش میپردازیم و مباحث مختلف در این زمینه را مرور میکنیم.

مجموعه چیست ؟
در ریاضیات، «مجموعه» (Set) به گرداورد یا مجموعهای یا دستهای از اعضای متمایز (غیرتکراری) میگویند که یک ویژگی مشترک دارند و این ویژگی را میتوان به راحتی توصیف و تعریف کرد. اگر به اطرافمان نگاه کنیم، با این تعریف، نمونههای زیادی از مجموعهها را خواهیم دید.
طبق تعریفی که گفتیم، یک مجموعه میتواند مجموعهای از چند تمبر یا سکه هر چیز دیگری باشد. برای مثال، اگر بخواهید بین حیواناتی که به خواب زمستانی میروند و حیواناتی که خواب زمستانی ندارند، تفاوت قائل شوید، میتوانید آنها را در دو مجموعه جدا قرار دهید که هر کدام ویژگیهای متفاوتی دارند. همه این مثالها راهی عالی برای فکر کردن به مجموعهها هستند.

مجموعهها در زندگی روزمره
کاربرد روزمره مجموعه چیست ؟ مجموعهها در اطراف ما به فراوانی یافت میشوند. مردم دوست دارند اشیا را بر اساس ویژگیهای مشترک دستهبندی کنند، زیرا این کار یافتن آنها را آسانتر و استفاده از آنها را سادهتر میکند. در اینجا چند نمونه را بیان میکنیم که هر روز مجموعهها را در آنجاها میبینید.
آشپزخانه: آشپزخانه مکانی عالی برای سازماندهی و پیدا کردن مجموعههاست. در ظروف غذاخوری، بشقابها و کاسهها جدا از هم هستند. حبوبات، برنج و سایر غلات به احتمال زیاد جدا از میوهها و سبزیجات نگهداری میشوند. قابلمهها و تابهها نیز در کشوی متفاوتی دور از پیشبند و رومیزی نگهداری میشوند.

با توجه به اینکه مجموعهها یکی از دروس ریاضی نهم نیز به شمار میآیند، برای آشنایی بیشتر با این درس، مطالعه مطلب زیر پیشنهاد میشود.
کتابخانه: تصور کنید که باید یک کتاب را بدون کمک مجموعهها پیدا کنید. خوشبختانه، سیستمی استفاده میشود که یافتن یک کتاب خاص را نسبتاً آسان میکند. کتابخانهها از سیستم ردهبندی کتابخانه کنگره یا سیستم ردهبندی دهدهی دیوئی برای سازماندهی کتابهای خود استفاده میکنند. بنابراین، کتابها و سایر مطبوعات مربوط به کتابخانه مانند مجلات و روزنامهها بر اساس رشته یا رشته تحصیلی در کنار هم قرار میگیرند. این امر تضمین میکند که کتابهای علوم در کنار سایر کتابهای علوم، کتابهای ریاضی با کتابهای ریاضی، و کتابهای کودکان با سایر کتابهای کودکان گروهبندی شوند.

لباسفروشی: اگر دقت کرده باشید، لباسفروشیها معمولاً لباسهایی را که ویژگیهای مشترکی دارند، در کنار یکدیگر قرار میدهند. مثلاً دسته شلوارهای جین یا دسته پیراهنهای آستینکوتاه. اگر بخواهیم اینها را با آن تعریف ابتدای متن بگوییم، اینگونه خواهد بود:
- مجموعه شلوارهای جین با ویژگی مشترک شلوار بودن و جین بودن
- مجموعه پیراهنهای آستینکوتاه با ویژگی مشترک پیراهن بودن و آستین کوتاه بودن

اکنون که دریافتیم مجموعه چیست و در زندگی روزمره با مجموعههای مختلفی سر و کار داریم که ویژگی یا ویژگیهای مشترکی دارند، میتوانیم این موضوع را بیان کنیم که در ریاضیات مجموعهها را چگونه و با چه نمادی نشان میدهند.
نمایش مجموعه در ریاضی
پیشتر گفتیم که مجموعه گروهی از چیزها است که ویژگی یا ویژگیهای مشترکی دارند. برای مثال، مجموعه میوهها گروهی از چیزها است که ویژگی مشترک میوه بودن را دارند. این مجموعه را به صورت زیر نمایش میدهیم (البته دقت کنید که چون تعداد میوهها زیاد است، همه آنها را نمایش ندادهایم و فقط چهار تای آنها را آوردهایم).

اگر دقت کنید مجموعه میوهها را درون دو «قلاب» یا «آکولاد» به شکل "{ }" قرار دادهایم. در ریاضیات از این نماد برای نشان دادن مجموعه استفاده میشود.
عضو مجموعه چیست ؟
در این بخش به این پرسش پاسخ میدهیم که عضو مجموعه چیست و چگونه تعلق آن به مجموعه را نشان میدهیم. در تعریف مجموعه، گفتیم که دستهای از چیزهاست که ویژگی مشترکی دارند. به هریک از این «چیزها»ی متمایز و منحصر به فرد، «عضو» (Element) مجموعه میگوییم. برای مثال، مجموعه نوشتافزار را در نظر بگیرید که در شکل زیر نمایش داده شده است (باز هم به دلیل تعداد زیاد آنها، همهشان را نیاوردهایم). در این مجموعه، کاغذ، چسب، مدادرنگی و قیچی عضو مجموعه هستند. همه اینها ویژگی مشترک نوشتافزار بودن را دارند و متمایز و جدا از یکدیگرند.
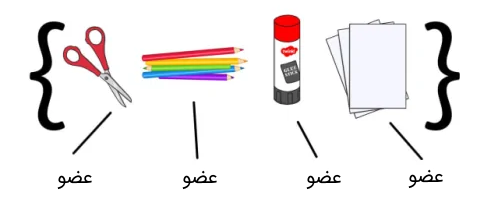
اگر بخواهیم نشان دهیم که عضوی متعلق به یک مجموعه است، از نماد استفاده میکنیم. در طرف مقابل، برای آنکه نشان دهیم چیزی عضو مجموعه نیست، نماد را به کار میبریم. حجمهای هندسی زیر، استفاده از این نمادها را به خوبی نشان میدهند.
این دو نماد را به این شکل بیان میکنیم:
- : متعلق است به
- : متعلق نیست به
نمایش مجموعه با جزئیات بیشتر
هنوز کار تمام نشده. واقعیت این است که نمیتوانیم در همه جا از تصویر اعضای مجموعه استفاده کنیم و آنها را در کنار یکدیگر با تصاویرشان نشان دهیم. همچنین، برای تفکیک و تمایز بین اعضای مجموعه باید از نشانهای استفاده کنیم که این تمایز را به خوبی نشان دهد. در ریاضیات از علامت «ویرگول» یا همان «کاما» برای جدا کردن اعضای مجموعه استفاده میکنیم. برای مثال، اگر بخواهیم فهرست خوراکیهایی را که در یک روز خاص از مغازه خریدهایم، به صورت یک مجموعه بنویسیم، خواهیم داشت:
{گوجهفرنگی , کلم بروکلی , گلابی , کره , تخممرغ , شیر , نان}
هرچیزی که درون این دو قلاب "{ }" قرار گیرد، عضو مجموعه است و چیزهای خارج از آن عضو مجموعه نیستند.
کمی بیشتر وارد وادی ریاضیات میشویم. فرض کنید میخواهیم مجموعه اعداد فرد را نشان دهیم. این کار را به صورت زیر انجام میدهیم:
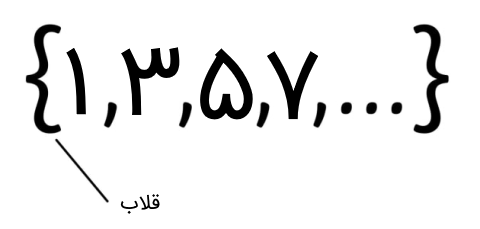
اما داستان سهنقطه این مجموعه چیست ؟ حتماً میدانید که اگر بخواهیم همه اعداد فرد را بنویسیم باید تا بینهایت ادامه دهیم که چنین چیزی عملاً امکانپذیر نیست. در این مواقع که ادامه مجموعه به بینهایت میل میکند، عضوهای ابتدایی مجموعه را مینویسیم و پس از آن از سهنقطه استفاده میکنیم. این نوع مجموعهها نام خاصی دارند که در ادامه با آن آشنا میشویم.
نامگذاری مجموعهها
برای نامگذاری مجموعهها کافی است در سمت چپ نام مجموعه را نوشته و یک مساوی بین آن و مجموعه قرار دهیم. مثلاً مجموعه اعداد فرد کوچکتر از ۸ را میتوان به صورت زیر نوشت:
{۷, ۵, ۳ ,۱} = مجموعه اعداد فرد کوچکتر از ۸
نوشتن نام مجموعه به این شکل کار رایجی نیست و معمولاً مجموعهها را با حروف انگلیسی بزرگ مانند A و B و C و... نمایش میدهند:
{۷, ۵, ۳ ,۱} = A
یا مجموعه روزهای هفته:
{جمعه , پنجشنبه , چهارشنبه , سهشنبه , دوشنبه , یکشنبه , شنبه} = B
همین مجموعه را اینگونه نیز میتوانیم بنویسیم:
{روزهای هفته} = B
نکته ۱: همانطور که گفتیم، اعضای مجموعه متمایز و منحصر به فرد هستند. این بدین معنی است که هر عضو فقط یک بار در مجموعه وجود دارد. مثلاً، مجموعه {۶ , ۶ , ۱۱} باید به صورت {۶ , ۱۱} نوشته شود.
نکته ۲: ترتیب نوشتن اعضای مجموعه مهم نیست. برای مثال، دو مجموعه {۵ , ۰ , ۴ , ۱} و {۰ , ۵ , ۱ , ۴} یکی هستند.
زیر مجموعه چیست ؟
دو مجموعه {4 ,2 ,1} = A و {5 ,4 ,3 ,2 ,1} = B داده شدهاند. مجموعه A را زیرمجموعه B میگوییم، زیرا هریک از اعضای A در B نیز هستند. این گفته را به علامت ریاضی زیر نشان میدهیم و میگوییم، A زیرمجموعه B است:
اگر بخواهیم مفهوم زیرمجموعه را برای این مثال به صورت بصری نشان دهیم، شکل زیر را خواهیم داشت.
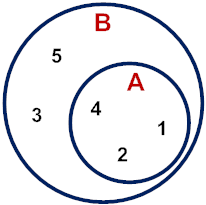
اکنون که زیرمجموعه را با مثال توضیح دادیم، میتوانیم تعریف ریاضی آن را بیان کنیم. در نظریه مجموعهها، مجموعه A به عنوان زیرمجموعهای از مجموعه دیگر B تعریف میشود، اگر همه اعضای مجموعه A در مجموعه B وجود داشته باشند. این تعریف را به صورت ریاضیاتی با نماد A ⊆ B نشان میدهیم.
زیرمجموعههای به غیر از خود مجموعه را «زیرمجموعه سره» (Proper Subset) مینامند. با این تعریف، مجموعه {2 ,1} یک زیرمجموعه سره از مجموعه {3 ,2 ,1} است، زیرا عضو 3 در مجموعه نخست وجود ندارد.
بنابراین، اگر A ⊆ B و A≠B، آنگاه A را یک زیرمجموعه سره از B مینامیم و آن را به صورت A⊂B مینویسیم.
تعداد زیرمجموعههای مجموعه A با n عضو، برابر با 2n است.
مجموعه جهانی چیست؟
مجموعه جهانی، مجموعهای است که تمام اعضای مجموعههایی که با آنها سر و کار داریم را در بر میگیرد. مجموعه جهانی را با نماد U یا E نمایش میدهند. دقت کنید که حرف U را با نماد ∪ (اجتماع دو مجموعه) اشتباه نگیرید. وقتی که با ستارهها سر و کار داریم، کهکشان راه شیری نمونه خوبی از مجموعه جهانی است. وقتی اعداد را در ریاضی مطالعه میکنیم، ممکن است مجموعه اعداد طبیعی را به عنوان مجموعه جهانی در نظر بگیریم. این مجموعه یک مجموعه جهانی محسوب میشود و زیرمجموعههای آن اعداد زوج، اعداد اول و... هستند. به عنوان یک مثال دیگر، در مطالعات جمعیت انسانی، مجموعه جهانی مجموعه همه افراد در جهان است. مجموعه همه افراد در هر کشور را میتوان زیرمجموعه این مجموعه جهانی دانست.
یک مجموعه جهانی میتواند یک مجموعه متناهی یا نامتناهی باشد. مجموعه اعداد طبیعی یک مثال معروف از یک مجموعه جهانی نامتناهی است. مجموعه جهانی از تمام اعضای زیرمجموعههایش و اعضای خودش تشکیل شده است.
برای بررسی بهتر مجموعه جهانی، سه مجموعه {۶ ,۴ ,۲} = A و {11 ,9 ,۷ ,۳ ,۱} = B و {11 ,8 ,4} = C را در نظر بگیرید. مجموعه جهانی را باید به گونهای در نظر بگیریم که همه اعضای این سه مجموعه عضو آن باشند. بنابراین، مجموعه جهانی را به صورت زیر تعریف میکنیم:
U = {1, 2, 3, 4, 6, 7, 8, 9, 11}
میبینیم که همه اعضای سه مجموعه بدون هیچ تکراری در مجموعه جهانی وجود دارند. تمام عناصر موجود در مجموعه جهانی منحصر به فرد هستند. مجموعههای A و B و C در مجموعه جهانی قرار دارند و زیرمجموعه آن هستند:
- A ⊂ U (مجموعه A زیرمجموعه U است).
- B ⊂ U (مجموعه B زیرمجموعه U است).
- C ⊂ U (مجموعه C زیرمجموعه U است).
مجموعه تهی چیست؟
مجموعه تهی مجموعهای است که هیچ عضوی ندارد. مجموعه تهی را با نماد Ø یا { } نشان میدهند. تنها یک مجموعه تهی وجود دارد، زیرا از نظر منطقی، تنها یک مجموعه وجود دارد که عضوی نداشته باشد.
به عنوان مثال، فرض کنید شخصی از شما خواسته است که مجموعه همه سالمندانی که کمتر از پنج سال دارند را پیدا کنید. واضح است که هیچ شهروند سالخورده زیر پنج سالی وجود ندارد، زیرا برای اینکه یک شهروند را سالمند در نظر بگیریم، باید بسیار بزرگتر از پنج سال داشته باشد. بنابراین مجموعه شما حاوی هیچ عنصری نیست و مجموعه تهی است. مثال دیگری از مجموعه تهی، مجموعه تمام اعداد زوج است که فرد نیز هستند. واضح است که یک عدد نمیتواند زوج و فرد باشد، بنابراین هیچ عنصری در این مجموعه وجود ندارد.
نکته: گاهی پیش میآید که مجموعه صفر و مجموعه تهی یکسان در نظر گرفته میشوند و حتی اصطلاحات (مجموعه صفر و مجموعه تهی) به اشتباه به جای یکدیگر استفاده میشوند. با داشتن درک روشنی از این دو مجموعه میتوان از این تصور غلط جلوگیری کرد. در ادامه، تفاوت این دو مجموعه را بیان میکنیم.
مجموعه صفر مجموعهای است که تنها عضو آن عدد صفر (0) است و آن را با {0} نشان میدهیم. دقت کنید که به 0 مانند هر عدد دیگری نگاه میکنیم و در اینجا، بحث ارزش عدد مطرح نیست. اما مجموعه تهی مجموعهای است که هیچ عضوی ندارد و با { } نمایش داده میشود. دقت کنید که مجموعه {Ø} تهی نیست.
از ویژگیهای مجموعه تهی میتوان به موارد زیر اشاره کرد:
- مجموعه تهی زیرمجموعه هر مجموعهای است.
- اشتراک مجموعه تهی با هر مجموعهای مجموعه تهی است.
- اجتماع مجموعه تهی با هر مجموعه دیگری برابر با آن مجموعه دیگر است.
نمودار ون چیست؟
نمودار وِن یکی از راههای نمایش بصری مجموعههاست که درک مفاهیم آنها را سادهتر میکند.
این نمودار یک مستطیل دارد که مجموعه جهانی را نشان میدهد. منظور از مجموعه جهانی، مجموعهای نیست که همه چیز در آن وجود دارد، بلکه مجموعهای است که همه چیزهایی که ما اکنون با آن سر و کار داریم در آن وجود دارند. مجاعضای موعهها نیز با دایرههایی درون مستطیلِ مجموعه جهانی رسم میشود.
شکل زیر یک نمودار ون را نشان میدهد. میبینیم که مجموعه جهانی U دارای این اعداد شامل U = {1, 2, 3, ... ,10} است و مجموعه A = {2, 4, 6, 8, 10} زیرمجموعه این مجموعه جهانی است.
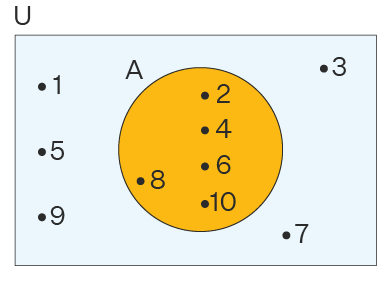
معمولاً دانشآموزان در تمایز بین اجتماع مجموعهها و مجموعه جهانی دچار سردرگمی میشوند. با نگاهی به تعاریف آنها میتوانیم تفاوت را بهتر درک کنیم. مجموعه جهانی مجموعهای از تمام اعضای همه مجموعههای مرتبط است و آن را با U نشان میدهیم. اجتماع مجموعهها یکی از عملیاتهای مجموعهها بین بین دو یا چند مجموعه است که در آن مجموعه حاصل شامل تمام اعضای متعلق به آن دو یا چند مجموعه اولیه است.
برای درک بهتر این تفاوت مثالی را بیان میکنیم. سه مجموعه U = {3, 5} و A = {a, b, c} و B = {e, f, g} را در نظر بگیرید. میخواهیم مجموعه جهانی U و اجتماع مجموعههای A و B را بنویسیم. مجموعه جهانی سه مجموعه به این صورت است: U = {a, b, c, e, f, g, 3, 5}. اجتماع بین A و B به صورت A ∪ B = {a, b, c, e, f, g} است. بنابراین، میتوانیم ببینیم که مجموعه جهانی شامل اعضای A و B و خود U است، در حالی که اجتماع A و B شامل فقط اعضای A و B است.
در آموزش «نمودار ون — از صفر تا صد (+ دانلود فیلم آموزش گام به گام)» میتوانید بیشتر با نمودار ون آشنا شوید.
مجموعه متناهی چیست؟
مجموعه متناهی مجموعهای است که تعداد محدودی عضو دارد. تعداد اعضای مجموعههای متناهی را میتوان شمارش کرد. توجه داشته باشید که همه مجموعههای متناهی قابل شمارش هستند، اما همه مجموعههای قابل شمارش متناهی نیستند. مجموعههای متناهی را میتوان به راحتی به صورت یک فهرست بیان کرد. به عنوان مثال، مجموعه اعداد طبیعی زوج کوچکتر از 11 را در نظر بگیرید: A = {2, 4, 6, 8, 10}. همانطور که میبینیم مجموعه A دارای 5 عضو است که یک عدد متناهی است و اعضای آن قابل شمارش هستند. در مجموعه متناهی روند شمارش اعضای مجموعه در جایی به پایان میرسد.
برای مجموعه متناهی میتوان ویژگیهای زیر را بیان کرد:
- یک زیرمجموعه سره از یک مجموعه متناهی متناهی است.
- اجتماع هر تعداد مجموعه متناهی، یک مجموعه متناهی خواهد بود.
- اشتراک دو مجموعه متناهی متناهی است.
- حاصل ضرب دکارتی مجموعههای محدود متناهی است.
- عدد اصلی یک مجموعه متناهی یک عدد محدود و برابر با تعداد اعضای مجموعه است.
- مجموعه توانی یک مجموعه متناهی متناهی است.
برای آشنایی بیشتر با عدد اصلی، پیشنهاد میکنیم مطلب «عدد اصلی مجموعه یا کاردینالیتی — به زبان ساده» را مطالعه کنید. همچنین، در مطلب «مجموعه توانی چیست؟ — از صفر تا صد» درباره مجموعه توانی توضیح دادهایم.
مجموعه نامتناهی چیست؟
در نظریه مجموعهها، مجموعه نامتناهی به مجموعهای میگویند که متناهی نیست. تعداد اعضای یک مجموعه نامتناهی بینهایت است، یعنی نمیتوانیم تعداد اعضا را دقیقاً تعیین کنیم. البته مجموعههای نامتناهی قابل شمارش وجود دارند. به عنوان مثال، مجموعه اعداد صحیح Z = {..., -2, -1, 0, 1, 2, ...} یک مجموعه نامتناهی قابل شمارش است، زیرا تعداد اعضای مجموعه بینهایت است و اعضای آن را میتوان در تناظر یک به یک با مجموعه اعداد طبیعی قرار داد و انها را یکی یکی شمرد. همانطور که در ابتدای آموزش اشاره کردیم، سایر اعضای یک مجموعه نامتناهی با نقطه نشان داده میشوند.
ویژگیهای مجموعه نامتناهی عبارتند از:
- اجتماع هر تعداد مجموعه نامتناهی یک مجموعه نامتناهی است.
- مجموعه توانی یک مجموعه نامتناهی نامتناهی است.
- اَبَرمجموعه یک مجموعه نامتناهی نامتناهی است.
- یک زیرمجموعه از مجموعه نامتناهی ممکن است متناهی یا نامتناهی باشد.
- مجموعههای نامتناهی میتوانند قابل شمارش یا غیرقابل شمارش باشند. به عنوان مثال، مجموعه اعداد حقیقی غیرقابل شمارش است، در حالی که مجموعه اعداد صحیح قابل شمارش است.
مجموعههای برابر
اگر همه عضوهای دو یا چند مجموعه یکسان باشند و تعداد آنها نیز برابر باشد، مجموعهها را مجموعههای برابر میگوییم. نماد مورد استفاده برای نشان دادن مجموعههای مساوی یا برابر، علامت "=" است، یعنی اگر مجموعههای A و B دو مجموعه برابر باشند، A = B نوشته میشود. میدانیم که ترتیب عناصر در مجموعهها مهم نیست. بنابراین، اگر A = {a, b, c, d} و B = {b, a, d, c} باشد، این دو مجموعه برابر هستند، زیرا عضوهای انها یکسان است و ترتیب آنها تأثیری بر برابریشان ندارد.
اکنون که با مفهوم مجموعههای برابر آشنا شدیم، به بررسی برخی از خواص مهم آنها میپردازیم که به درک و شناساییشان کمک میکند:
- ترتیب اعضای مجموعهها برابری آنها تأثیر نمیگذارد.
- مجموعههای برابر دارای کاردینالیتی یکسان هستند، یعنی تعداد اعضای یکسانی دارند.
- اگر دو مجموعه زیرمجموعه یکدیگر باشند، آنگاه مجموعهها برابر هستند، یعنی اگر A ⊆ B و B ⊆ A، آنگاه A = B.
- مجموعههای برابر باید اعضای برابر داشته باشند.
عملیات روی مجموعه چیست ؟
عملیات روی مجموعه، عملیاتی است که روی یک یا چند مجموعه اعمال میشود تا به هدف دلخواه برسیم. چهار عملیات اصلی برای مجموعهها وجود دارد که عبارتند از: اجتماع مجموعهها، اشتراک مجموعهها، متمم یک مجموعه، تفاضل مجموعهها. درادامه بیان میکنیم که عملیات روی مجموعه چیست و چه مفهومی دارد.
اجتماع مجموعهها
اجتماع دو مجموعه A و B که آن را با A∪B نشان میدهیم (میخوانیم A اجتماع B یا اجتماع A با B) مجموعهای از اعضای متمایز است که به مجموعه A و B یا هر دو تعلق دارند. تعداد عناصر در A∪B با n(A∪B) = n(A) + n(B) - n(A∩B) داده می شود، که در آن n(X) تعداد عناصر مجموعه X است. برای درک بهتر عملیات اجتماع مجموعهها مثالی را بررسی میکنیم. اگر A = {1, 2, 3, 4} و B = {4, 5, 6, 7}، آنگاه اجتماع A و B برابر است با A ∪ B = {1, 2, 3, 4, 5, 6, 7}.
برای نمایش اجتماع مجموعهها با نمودار ون، ابتدا به یک مجموعه جهانی نیاز داریم که دو مجموعه داده شده P و Q زیرمجموعه های آن هستند. نمودار ون زیر اجتماع بین مجموعههای P و Q را نشان میدهد.
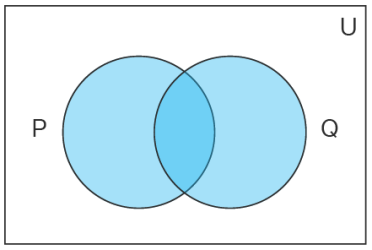
در نمودار ون که در شکل بالا داده شده است، ناحیه آبی رنگ اجتماع مجموعههای P و Q را نشان میدهد. این شکل نشان میدهد که اجتماع بین این مجموعهها شامل تمام عضوهای موجود در P یا Q یا هر دو مجموعه است.
اشتراک مجموعهها
اشتراک دو مجموعه A و B را که با A∩B (میخوانیم A اشتراک B یا اشتراک A با B) نشان میدهیم، مجموعهای از اعضای مشترکی است که هم به مجموعه A و هم به مجموعه B تعلق دارند. تعداد اعضای A∩B با n(A∩B) = n(A)+n(B)−n(A∪B) محاسبه میشود، که در آن n(X) تعداد اعضای مجموعه X است. برای درک بهتر اشتراک مجموعهها، مثالی را بیان میکنیم. اگر A = {1, 2, 3, 4} و B = {3, 4, 5, 7}، آنگاه اشتراک A و B به صورت A ∩ B = {3, 4} خواهد بود.
وقتی در نموادار ون دایرهها همپوشانی داشته باشند، یعنی بین دو مجموعه اشتراک وجود دارد، در حالی که دایرههایی که فاقد همپوشانیاند هیچ عنصر مشترکی نیز ندارند. شکل زیر اشتراک مجموعهها را با استفاده از نمودار ون نشان میدهد. مجموعهها A = {1, 2, 3, 4, 5} و B = {3, 4, 6, 8} هستند. بنابراین A ∩ B = {3, 4}.

تفاضل مجموعهها
تفاضل بین مجموعهها به معنای کم کردن اعضای یک مجموعه از مجموعه دیگر است که مفهوم مشابهی با تفاضل اعداد دارد. تفاضل مجموعه B از مجموعه A که به صورت A - B نشان داده میشود، شامل تمام اعضایی از مجموعه A است که در مجموعه B نیستند. برای درک بهتر تفاضل مجموعهها، یک مثال ساده را بررسی میکنیم. اگر A = {1, 2, 3, 4} و B = {3, 4, 5, 7} را داشته باشیم، آنگاه تفاضل بین مجموعههای A و B به صورت A - B = {1, 2} داده می شود.
متمم مجموعه چیست ؟
اما متمم یک مجموعه چیست ؟ متمم مجموعه A مجموعهای است که اعضای آن شامل همه عضوهای مجموعه جهانی است که در A نیستند. متمم مجموعه را با نماد c یا ' در بالای نام مجموعه نیز نمایش میدهند. برای مثال متمم مجموعه A را با Ac یا 'A نمایش میدهیم.
یک مثال ساده از دو مجموعه متمم، مجموعه اعداد زوج و فرد هستند. مجموعه جهانی را مجموعه اعداد طبیعی در نظر میگیریم:
N = {1, 2, 3, 4, 5, 6, ...}
میدانیم که مجموعه اعداد فرد به صورت زیر هستند:
O = {1, 3, 5, ...}
مکمل مجموعه اعداد فرد، همان مجموعه اعداد زوج خواهد بود، زیرا مجموعه اعداد زوج، شامل همه اعضای مجموعه اعداد طبیعی است که در مجموعه اعداد فرد نیستند:
E = {2, 4, 6, ...}
بنابراین، میتوان نوشت:
Oc = E یا Ec = O
متمم مجموعه جهانی مجموعه تهی است.
مجموعه یکانی چیست؟
مجموعه یکانی مجموعهای است که فقط یک عضو دارد. برای نمونه، مجموعههای زیر همگی مجموعه یکانی هستند، زیرا فقط یک عضو دارند:
- عددهای طبیعی بین 5 و 7، یعنی مجموعه {6} که فقط یک عضو دارد.
- عددهای طبیعی زوج که اول باشند، یعنی مجموعه {2} که فقط یک عضو دارد.
- شمارندههای اول عدد یعنی مجموعه که فقط یک عضو دارد.
مثالهای مجموعه
در این بخش، مثالهای متنوعی را از مجموعهها حل میکنیم.
مثال اول مجموعه
با توجه به آنچه که گفتیم، آیا {۲ , ۳ , ۳ , ۱} یک مجموعه است؟
پاسخ: خیر. همانطور که گفتیم، اعضای یک مجموعه باید متمایز و منحصر به فرد باشند. به همین دلیل، باید آن را به صورت {۲ , ۳ , ۱} نوشت تا بتوانیم به آن مجموعه بگوییم.
مثال دوم مجموعه
آیا دو مجموعه {۹ , ۷ , ۵ , ۳ , ۱} و {۷ , ۹ , ۵ , ۳ , ۱} یکی هستند؟
پاسخ: بله، این دو مجموعه یکی هستند، زیرا ترتیب اعضا در مجموعه مهم نیست.
مثال سوم مجموعه
مجموعههای A و B به صورت زیر تعریف شدهاند:
A = {3, 5, 7, 8} , B = {x, y, z}
درست یا نادرست بودن گزارههای زیر را مشخص کنید.
الف) 3 ∋ A
ب) 3 ∈ B
ج) x ∉ A
د) z ∈ B
هـ) 8 ∈ B
پاسخ الف: درست. میبینیم که 3 عضوی از مجموعه A است.
پاسخ ب: نادرست. عدد 3 عضو مجموعه A است.
پاسخ ج: درست. x عضو مجموعه B است و عضو A نیست.
پاسخ د: درست. z عضو مجموعه B است.
پاسخ هـ: نادرست. ۸ عضو مجموعه A است.
مثال چهارم مجموعه
مجموعههای زیر را به صورت ریاضی بنویسید.
الف) مجموعه تمام اعداد زوج مثبت کوچکتر یا مساوی 10.
ب) مجموعه تمام حروف در کلمه "IRAN".
ج) مجموعه تمام اعداد صحیح بزرگتر از 3 و کوچکتر از 16 و بخشپذیر بر 3.
د) مجموعه تمام اعداد صحیح بزرگتر از 5 و کوچکتر از 35 و بخشپذیر بر 5.
هـ) مجموعه تمام اعداد اول بخشپذیر بر 3.
و) مجموعه تمام اعدادی که قدر مطلق آنها برابر با 7 است.
پاسخ الف: {8 , 6 ,4 ,2}
پاسخ ب: {I, R, A, N}
پاسخ ج: {15 , 12 ,9 ,6}
پاسخ د: {30 , 25 , 20, 15 ,10}
پاسخ هـ: {3}
پاسخ و: {7 ,7-}
مثال پنجم مجموعه
مجموعههای A و B و C و D به صورت زیر تعریف شدهاند:
A = {2, 3, 4, 5, 6, 7}, B = {3, 5, 7}, C = {3, 5, 7, 20, 25, 30}, D = {20, 25, 30}
درست یا نادرست بودن هریک از گزارههای زیر را مشخص کنید:
الف) A ⊂ B
ب) B ⊂ A
ج) B ⊄ C
د) C ⊂ D
هـ) D ⊄ A
پاسخ الف: نادرست
پاسخ ب: درست
پاسخ ج: نادرست
پاسخ د: نادرست
پاسخ هـ: درست
مثال ششم مجموعه
مجموعههای A و B و C و D مثال قبل را در نظر بگیرید:
A = {2, 3, 4, 5, 6, 7}, B = {3, 5, 7}, C = {3, 5, 7, 20, 25, 30}, D = {20, 25, 30}
حاصل عبارات زیر را بنویسید:
الف) A ⋃ B
ب) A ⋂ B
ج) B ⋂ C
د) C ⋃ B
هـ) D ⋂ C
و) (A ⋂ B) ⋂ C
ز) (A ⋃ B) ⋂ (C ⋃ D)
ح) (A ⋃ B) ⋃ (C ⋃ D)
پاسخ الف: A ⋃ B = A
پاسخ ب: A ⋂ B = B
پاسخ ج: B ⋂ C = B
پاسخ د: C ⋃ B = C
پاسخ هـ: D ⋂ C = D
پاسخ و: (A ⋂ B) ⋂ C = B
پاسخ ز: (A ⋃ B) ⋂ (C ⋃ D) = B
پاسخ ح: (A ⋃ B) ⋃ (C ⋃ D) = {2, 3, 4, 5, 6, 7, 20,25,30}
مثال هفتم مجموعه
در شکل زیر یک نمودار ون نشان داده شده است که بیانگر مجموعههای A و B است. اعضای مجموعه جهانی را برای زیرمجموعههای دادهشده آن، یعنی A و B، تعیین کنید.
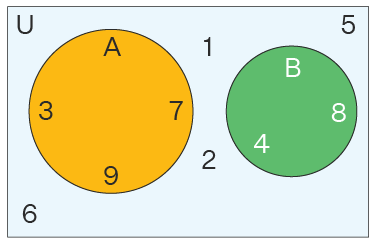
پاسخ: میدانیم که هر مجموعه جهانی با یک مستطیل و مجموعههای زیرمجموعه آن با دایرهها نمایش داده میشوند. در اینجا، دو مجموعه A = {3, 7, 9} و B = {4, 8} را داریم. بدیهی است که A و B مجموعههای متمایزی هستند، زیرا هیچ عضو مشترکی ندارند. همچنین اعضایی که در A و B موجود نیستند، در مجموعه جهانی وجود دارند. میدانیم که مجموعه جهانی مجموعهای است که از تمام اعضای مجموعههای مورد بحث و اعضای خود تشکیل شده است. بنابراین، مجموعه جهانی در این مثال U = {1, 2, 3, 4, 5, 6, 7, 8, 9} است.
مثال هشتم مجموعه
مجموعه جهانی U = {2, 4, 5, 14, 17, 28, 35, 52} را در نظر بگیرید. اعضای مجموعههای زیر را بنویسید:
{x عاملی از ۱۰ است :x} = A
{x ضریبی از ۱4 است :x} = B
پاسخ: مجموعه جهانی U = {2, 4, 5, 14, 17, 28, 35, 52} را داریم. عاملهای عدد ۱۰ در مجموعه A، اعداد ۲ و ۵ هستند. همچنین، مضربهای 14 در این مجموعه 14 و 28 هستند. بنابراین، دو مجموعه A و B را میتوان اینگونه نوشت:
A = {2, 5}
B = {14, 28}
معرفی فیلم آموزش ریاضی و آمار (۱) - پایه دهم علوم انسانی
یکی از آموزشهای ویدیویی دوره دبیرستان فرادرس، «آموزش ریاضی و آمار (۱) - پایه دهم علوم انسانی» است که به طور ویژه مربوط به دانشآموزان رشته علوم انسانی است. این آموزش ویدیویی در قالب چهار درس و در زمان ۶ ساعت و ۱۹ دقیقه تدوین شده است. در درس یکم، معادله درجه دوم مورد بحث قرار گرفته که شامل مطالب اصلی درس، نکات مهم و مثالهای حل شده است. در درس دوم، موضوع مهم تابع ارائه شده و در آن، به موارد مهمی از قبیل تعریف ضابطه و تابع، رسم آن، دامنه و برد تابع و... پرداخته شده است. کار با دادههای آماری موضوع درس سوم است. در نهایت، در درس چهارم به طور کامل، مطالب کتاب درسی درباره نمایش دادهها ارائه شده است.
- برای مشاهده فیلم آموزش ریاضی و آمار (۱) - پایه دهم علوم انسانی + اینجا کلیک کنید.
معرفی فیلم آموزش ریاضی پایه دانشگاهی
یکی از آموزشهایی که برای آشنایی بیشتر با ریاضیات پایه دانشگاهی میتوانید به آن مراجعه کنید، آموزش ریاضی پایه دانشگاهی است. این آموزش که مدت آن ۱۲ ساعت و ۴۶ دقیقه است، در قالب ۱۰ درس تهیه شده است.
در درس اول، مجموعهها، مجموعه اعداد، توان، ب.م.م و ک.م.م معرفی شدهاند. موضوعات درس دوم، چندجملهایها و اتحاد و تجزیه است. در درس سوم، نامساویها، نامعادلات، طول پارهخط، ضریب زاویه و معادله خط مورد بحث قرار گرفتهاند. مثلثات موضوع مهم درس چهارم است. تصاعد حسابی و هندسی در درس پنجم بررسی شدهاند. تابع و دامنه و برد آن موضوعات مهم درس ششم هستند. در درس هفتم، تساوی دو تابع، اعمال جبری روی تابع و ترکیب توابع ارائه شدهاند. در درس هشتم به توابع زوج و فرد، تابع یک به یک و تابع وارون پرداخته شده است. انواع توابع از قبیل تابع ثابت، تابع همانی، تابع علامت، تابع قدر مطلق و تابع جزء صحیح موضوع درس نهم هستند. در نهایت، در درس دهم توابع نمایی و لگاریتمی مورد بحث قرار گرفتهاند.
- برای مشاهده فیلم آموزش ریاضی پایه دانشگاهی + اینجا کلیک کنید.
آزمون مجموعه در ریاضی
۱. در ریاضیات، مجموعه چه ویژگیهای اصلیای دارد که باعث تمایز آن از سایر گروهبندیها میشود؟
فقط شامل اشیای فیزیکی و ملموس میشود.
بدون نیاز به هرگونه شرط یا ویژگی تعریف میشود.
دارای اعضای متمایز و غیرتکراری با ویژگی مشترک است.
همیشه تعداد اعضای آن نامشخص باقی میماند.
مجموعه در ریاضیات گروهی از اعضای متمایز و غیرتکراری است که همه یک ویژگی مشترک دارند. این عامل «تمایز اعضا و داشتن ویژگی توصیفپذیر» مهمترین تفاوت مجموعه با سایر گروهبندیهاست. «تعداد نامشخص»، «فقط اشیای فیزیکی» یا «تعریف بدون شرط» با تعریف مجموعه در ریاضی سازگار نیستند؛ زیرا مجموعه میتواند متناهی یا نامتناهی باشد، هم اشیای غیرملموس مثل اعداد را شامل میشود و هم باید ویژگی مشخص برای شناسایی اعضا داشته باشد.
۲. در مجموعههای ریاضی، تمایز میان اعضا به چه معناست و چرا این ویژگی اهمیت دارد؟
همه اعضای مجموعه باید یک ویژگی مشترک داشته باشند.
ترتیب قرار گرفتن اعضا در مجموعه مهم است.
هر عضو مجموعه باید با دیگر اعضا متفاوت باشد و تکرار نشود.
اعضا میتوانند هر تعداد بار که خواستند در مجموعه تکرار شوند.
در مجموعههای ریاضی، منظور از تمایز اعضا این است که هر عضو باید یکتا باشد و هیچ تکراری بین اعضا وجود نداشته باشد.
۳. کدام اصل هنگام نوشتن مجموعهها در ریاضیات باعث میشود ترتیب و تکرار اعضا اثری در تعریف مجموعه نداشته باشد؟
هر عضو باید عدد باشد و نه شی دیگر.
برای نامگذاری فقط حروف کوچک استفاده میشود.
اعضا باید متمایز و غیر تکراری باشند.
هر مجموعه فقط یک زیرمجموعه دارد.
در ریاضیات، اصل «اعضا باید متمایز و غیر تکراری باشند» تضمین میکند که اگر عضوی چند بار تکرار شود، فقط یک بار در مجموعه لحاظ میشود و ترتیب نوشتن اعضا اهمیتی ندارد. به همین دلیل، مجموعههایی با همان اعضا اما ترتیب متفاوت، برابراند و تکرار عضو اثری در ساختار مجموعه ندارد.
۴. اگر عضوی در یک مجموعه نباشد، برای نشان دادن این موضوع در ریاضیات از چه نمادی استفاده میشود و این علامت چه مفهومی دارد؟
نماد که نشاندهنده عضویت عضو در مجموعه است.
نماد که بیانگر برابری دو مجموعه است.
نماد که نشاندهنده نبودن عضو در مجموعه است.
نماد که بیانگر زیرمجموعه بودن است.
هنگامی که از نماد «» استفاده میشود، منظور این است که یک عضو بخشی از مجموعه مورد نظر نیست. این علامت دقیقا مفهوم تعلق نداشتن عضو را میرساند.
۵. در یک کتابخانه، کتابها بر اساس ژانر در قفسههای جدا قرار گرفتهاند. این روش سازماندهی چه مفهومی را از نظر ریاضی نشان میدهد؟
ترتیبگذاری اعضا بر اساس اولویت عددی
تعیین تعداد اعضا برای ساخت زیرمجموعه
دستهبندی اشیا با ویژگی مشترک مانند یک مجموعه
نمایش مجموعهها با سهنقطه برای نامتناهی بودن
وقتی کتابها بر اساس ژانر جدا میشوند، در واقع هر ژانر به عنوان مجموعهای از کتابها با یک ویژگی مشترک همچون مجموعه در ریاضی شناخته میشود. در این حالت ویژگی مشترک همان ژانر است. برخلاف «ترتیبگذاری اعضا بر اساس اولویت عددی» که به ترتیببندی مربوط است و در مجموعهها ترتیب اهمیت ندارد، یا «تعیین تعداد اعضا برای ساخت زیرمجموعه» که به ساخت زیرمجموعهها وابسته است و در این مثال مطرح نیست، و همچنین «نمایش مجموعهها با سهنقطه برای نامتناهی بودن» بیشتر درباره نمایش مجموعههای بزرگ کاربرد دارد، مفهوم اصلی همان دستهبندی بر اساس ویژگی مشترک است که دقیقا با تعریف مجموعه در ریاضیات مطابقت دارد.
۶. برای یک مجموعه با n عضو، چه روشی برای محاسبه تعداد زیرمجموعهها وجود دارد و این اصل بر چه مبنای منطقی استوار است؟
هر مجموعه فقط زیرمجموعههای برابر با تعداد اعضایش دارد، چون هر عضو یک زیرمجموعه میسازد.
هر عضو فقط یک بار میتواند زیرمجموعه تشکیل دهد و تعداد زیرمجموعهها نصف تعداد اعضاست.
تعداد زیرمجموعهها برابر است با دو به توان n، چون هر عضو میتواند باشد یا نباشد.
تعداد زیرمجموعهها برابر است با n مضروب در خودش، چون هر عضو باید با عضو دیگر ترکیب شود.
در محاسبه تعداد زیرمجموعهها برای مجموعههای n عضوی، دلیل استفاده از دو به توان n این است که هر عضو میتواند در هر زیرمجموعه وجود داشته باشد یا نداشته باشد. بنابراین هر عضو دو حالت دارد و حاصلضرب این دو حالت برای n عضو، همان دو به توان n است.
۷. در کدام حالت بیان میشود که یک مجموعه A زیرمجموعه مجموعه B است و چه زمانی این زیرمجموعه، زیرمجموعه سره نامیده میشود؟
فقط وقتی اعضای A بخشی از B باشند و هیچ برابری وجود نداشته باشد، زیرمجموعه و اگر برابر شوند، زیرمجموعه سره است.
زمانی که همه اعضای A در B باشند و شاید هر دو برابر باشند، زیرمجموعه و اگر A و B دقیقا برابر باشند، زیرمجموعه سره است.
هنگامی که تمام اعضای A در B باشند و A میتواند با B برابر باشد، آنگاه زیرمجموعه بوده و در صورتی که A و B برابر نباشند، زیرمجموعه سره است.
زمانی که حداقل یک عضو مشترک وجود داشته باشد، زیرمجموعه و اگر همه اعضا یکی باشند، زیرمجموعه سره است.
وقتی همه اعضای یک مجموعه مانند A در مجموعه دیگر مانند B باشند، میگوییم A زیرمجموعه B است و این حالت حتی اگر A و B برابر باشند نیز صادق است. اما اگر تمامی اعضای A در B باشند و در عین حال مجموعه A و B دقیقا برابر نباشند، مجموعه A را زیرمجموعه سره (Proper Subset) مجموعه B مینامیم.
۸. چه نکتهای باعث میشود اجتماع مجموعهها و مجموعه جهانی دو مفهوم متمایز باشند؟
مجموعه جهانی فقط شامل اعضای مشترک چند مجموعه است.
اجتماع شامل همه اعضای جهان است و مجموعه جهانی فقط تعدادی را دارد.
اجتماع همیشه بزرگتر از مجموعه جهانی است.
اجتماع فقط اعضای مجموعههای دادهشده را دربرمیگیرد، اما مجموعه جهانی اعضای بیشتری را شامل میشود.
مجموعه جهانی (Universal Set) تمام اعضایی را که در یک موضوع مورد بحث هستند در بر میگیرد و بسته به تعریف مسئله میتواند بسیار وسیعتر از مجموع اعضای چند مجموعه باشد. اما اجتماع صرفا اعضایی را شامل میشود که در دستکم یکی از مجموعههای مشخص شده حضور دارند.
۹. برای تشخیص مجموعه تهی و مجموعه صفر در حل یک مسئله ریاضی، کدام ویژگی و نماد به درستی آنها را از یکدیگر متمایز میکند؟
مجموعه تهی همیشه شامل یک عضو غیرصفر است و با {0} نوشته میشود.
مجموعه تهی هیچ عضوی ندارد و با نماد Ø یا {} نشان داده میشود.
مجموعه تهی و مجموعه صفر هر دو دقیقا یک عضو داشته و با {0} مشخص میشوند.
مجموعه صفر دارای هیچ عضوی نیست و با نماد ∅ نمایش داده میشود.
مجموعه تهی شامل هیچ عضو نیست و نمادهای Ø و {} برای آن استفاده میشود.
۱۰. تفاوت اصلی مجموعه متناهی و نامتناهی در چیست و این اختلاف چه اثری بر شمارشپذیری اعضا دارد؟
مجموعه متناهی اعضای قابل شمارش محدود دارد و نامتناهی اعضای بیپایان و گاهی غیرقابل شمارش دارد.
مجموعه متناهی فقط یک عضو دارد ولی نامتناهی اعضای مختلف دارد.
در مجموعه متناهی تکرار اعضا مجاز است اما در نامتناهی مجاز نیست.
مجموعه متناهی فقط عدد صحیح دارد و نامتناهی عدد اعشاری دارد.
مجموعه متناهی تعداد محدودی عضو دارد که میتوان همه آنها را شمرد، اما مجموعه نامتناهی اعضای بیشماری دارد و در برخی موارد مانند اعداد حقیقی اصلا شمارشپذیر نیست. عبارت «مجموعه متناهی اعضای قابل شمارش محدود دارد و نامتناهی اعضای بیپایان و گاهی غیرقابل شمارش دارد» به درستی تفاوت را نشان میدهد. گزینههای شامل محدودیت به اعداد صحیح یا مجاز بودن تکرار و تعداد عضوها هیچکدام بر اساس تعریف مجموعه متناهی و نامتناهی صحیح نیستند.
۱۱. در نمودار ون، مجموعه جهانی و زیرمجموعهها معمولا چگونه نمایش داده میشوند و این نمودار چه ارتباطی با فهم عملیات مجموعهای دارد؟
مجموعه جهانی به صورت یک مستطیل و زیرمجموعهها با دایرههای داخل آن نشان داده میشوند.
زیرمجموعهها با مستطیل و مجموعه جهانی با خط شکسته نمایش داده میشود.
هر مجموعه با یک مثلث و مجموعه جهانی با دایره بزرگ رسم میشود.
همه مجموعهها به کمک چند خط مستقیم و بدون شکلهای بسته نمایش داده میشوند.
در نمودار ون، معمول است که مجموعه جهانی به شکل مستطیل نمایش داده میشود و زیرمجموعهها به صورت دایرههایی درون این مستطیل قرار میگیرند. این نمایش بصری باعث میشود ارتباط بین مجموعهها مانند اجتماع، اشتراک و تفاوت به راحتی با بخشهای همپوشان یا جداگانه در نمودار قابل مشاهده باشد.













متمایز به معنای جدا از هم نیست!🗿
یعنی نباید عضو تکراری داخل مجموعه باشه
سلام خدمت شما؛
نکته بیان شده صحیح است و اصلاحات لازم در متن اعمال شد.
از همراهی شما با مجله فرادرس سپاسگزاریم.
سلام؛مطالب مفهومی و عالی بودند.همچنین مجموعه داریم:
A=(2,3,(5,6,7),(a,b.c))
تشکر پاسخ دهید.
با سلام خدمت شما؛
در آخرین بخش از این مجموعه عنصری به شکل (a,b.c) داریم که اگر یک عنصر واحد در مجموعه است، باید بهصورت (a,b,c) نوشته شود و اگر زیرمجموعه است، باید به شکل {(a,b,c)} نوشته شود. چون هیچکدام از این دو مورد رعایت نشده است، بنابراین نمیتوانیم عبارت بالا را یک مجموعه در نظر بگیریم.
از همراهی شما با مجله فرادرس سپاسگزاریم.
سلام
ممنون بابت این مطلب کامل و مفید
میخواستم بدونم برای جمله
همه مجموعههای متناهی قابل شمارش هستند، اما همه مجموعههای قابل شمارش متناهی نیستند.
میتوانید مثال بزنید؟!
مهرا درست مجموعه یعنی همه عضو ولی بعضی از عضو قابل شمارش نیستند