ساخت شبکه عصبی در پایتون – Neural Network با Python به زبان ساده
بهترین راه برای درک مفهوم و چگونگی عملکرد «شبکه عصبی» (Neural Network)، ساخت آن است. در این مطلب، روش ساخت یک شبکه عصبی با بهرهگیری از «زبان برنامهنویسی پایتون» (Python Programming Language) آموزش داده شده است. شبکههای عصبی (NN) که به آنها «شبکههای عصبی مصنوعی» (Artificial Neural Networks | ANN) نیز گفته میشود، یکی از الگوریتمهای یادگیری در «یادگیری ماشین» (Machine Learning) به شمار میآید که براساس مفهوم زیستی شبکههای عصبی بنا نهاده شده است. در این مقاله سعی داشتهایم بهطور جامع به ساخت شبکه عصبی در پایتون بپردازیم.


مقدمهای بر ساخت شبکه عصبی در پایتون
«اندرو بولزیوک» (Andrey Bulezyuk) کارشناس یادگیری ماشین آلمانی و دارای سالها تجربه، در این رابطه میگوید: «شبکههای عصبی انقلابی در یادگیری ماشین محسوب میشوند، زیرا قادر به مدلسازی کارآمد انتزاعات پیچیده در طیف وسیعی از رشتهها و صنایع هستند». اساسا، یک شبکه عصبی ترکیبی از مولفههای زیر است:
- یک لایه ورودی که دادهها را دریافت میکند
- یک لایه پنهان
- یک لایه خروجی
- وزنهای بین لایهها
- یک تابع فعالسازی تعمدی برای هر لایه پنهان (در این مطلب از تابع فعالسازی سیگموئید استفاده شده است.)
چندین نوع شبکه عصبی وجود دارد. در این راهنمای ساخت شبکه عصبی در پایتون یک «شبکه عصبی پیشخور» (Feedforward Neural Network) یا «شبکه عصبی پرسپترون» (Perception Neural Networks) ساخته خواهد شد. این نوع از شبکه عصبی مصنوعی دادهها را مستقیما از جلو به عقب بازپخش میکند. آموزش نورونهای پیشخور اغلب نیازمند «بازگشت به عقب یا انتشار معکوس» (back-propagation) است که شبکهای با مجموعههای متناظر ورودیها و خروجیها محسوب میشود. هنگامی که دادههای ورودی به «نورون» (neuron) انتقال پیدا کردند، پردازش میشوند و یک خروجی تولید میشود. در تصویر زیر، نموداری که ساختار یک شبکه عصبی ساده را نمایش میدهد آورده شده است.
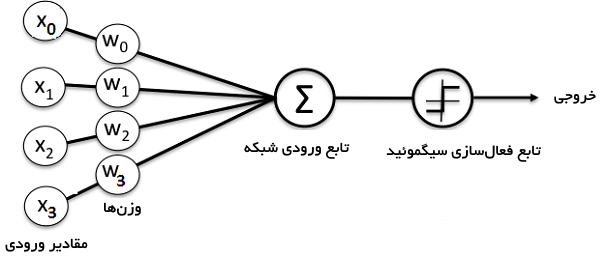
بهترین راه برای درک اینکه شبکههای عصبی چگونه کار میکنند، فراگیری این است که چگونه میتوان یک شبکه عصبی در پایتون را از پایه بدون استفاده از هرگونه کتابخانهای ساخت. در این مطلب، چگونگی ساخت یک شبکه عصبی با پایتون به بیان ساده ارائه میشود.
طرح مسئله ساخت شبکه عصبی در پایتون
در جدول زیر مساله موجود نشان داده شده است.
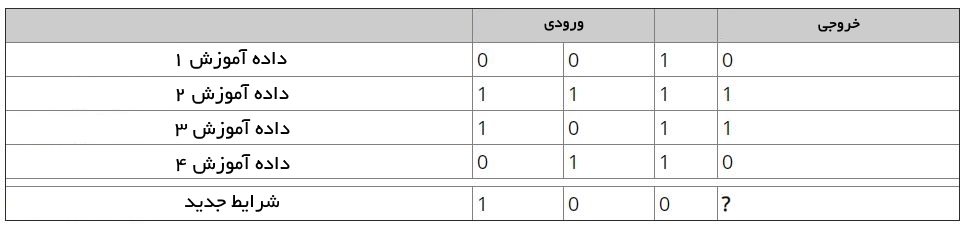
اکنون، یک شبکه عصبی در پایتون که میتواند مقدار خروجی را برای مجموعه دادههای جدید به درستی پیشبینی کند ساخته خواهد شد. همانطور که از جدول مشهود است، مقدار خروجی همیشه مساوی با اولین مقدار در قسمت ورودی خواهد بود. بنابراین، انتظار میرود مقدار خروجی برای شرایط جدید (New Situation) برابر با ۱ باشد. در ادامه این مساله بررسی میشود که آیا میتوان از کد پایتونی استفاده کرد که نتیجه مشابهی داشته باشد.
ساخت کلاس شبکه عصبی
در این بخش، هدف ساخت یک کلاس NeuralNetwork در پایتون به منظور آموزش دادن نورونها برای ارائه پیشبینی صحیح است. این کلاس همچنین دارای دیگر «توابع کمک کننده» (helper functions) نیز هست.
با وجود اینکه از یک کتابخانه شبکه عصبی در پایتون برای ساخت این شبکه عصبی ساده استفاده نمیشود، کتابخانه NumPy برای کمک به انجام محاسبات «ایمپورت» میشود. کتابخانه دارای چهار متد مهم زیر است:
- exp: برای تولید «تابع نمایی» (natural exponential)
- array: برای تولید یک ماتریس
- dot: برای ضرب ماتریسها
- random: برای تولید اعداد تصادفی (توجه به این نکته نیز لازم است که از اعداد تصادفی برای حصول اطمینان از توزیع کارآمد آنها استفاده میشود.)
اعمال تابع سیگموئید
در اینجا از تابع «سیگموئید» (Sigmoid) استفاده خواهد شد که یک منحنی مشخصه S شکل به عنوان تابع فعالسازی برای شبکه عصبی در پایتون ترسیم میکند.
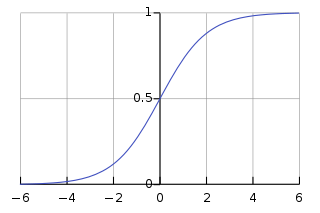
این تابع هر مقدار را به یک مقدار از ۰ تا ۱ نگاشت میکند و کمک میکند تا مجموع وزنی ورودیها «نرمالسازی» (normalize) شوند. بعد از آن، مشتق تابع سیگموئید برای کمک به محاسبه تنظیمات اساسی وزنها گرفته میشود. خروجی تابع سیگموئید میتواند برای تولید مشتق آن مورد استفاده قرار بگیرد. برای مثال، اگر متغیر خروجی برابر با «x» است، مشتق آن برابر با «(x * (1-x» خواهد بود.
در واقع، اگر خروجی تابع سیگموئید متغیر x باشد، میتوان مشتق «تابع سیگموئید» را با استفاده از این خروجی محاسبه کرد. آنچه در اینجا هم بیان شده، بر همین مفهوم دلالت دارد. یعنی، اگر خروجی تابع سیگموئید متغیر x باشد، مشتق خود تابع سیگموئید برابر با مقدار بیان شده است. به بیان ریاضی، اگر فرض کنیم تابع سیگموئید است، مشتق آن برابر با خواهد بود. با کمی سادهسازی، خواهیم دید که .
آموزش دادن مدل
در این گام به شبکه عصبی در پایتون آموزش داده میشود که پیشبینی دقیقی انجام دهد. هر ورودی یک وزن (مثبت یا منفی) خواهد داشت. این امر دلالت بر آن دارد که یک ورودی دارای عدد بزرگی از وزنهای مثبت یا عدد بزرگی از وزنهای منفی، نتیجه خروجی را بیشتر تحت تاثیر قرار خواهد داد.
این نکته را نیز باید به خاطر داشت که مقداردهی اولیه وزنها با تخصیص یک عدد تصادفی به هر وزن به وقوع خواهد پیوست. در ادامه روال فرآیند آموزش مورد استفاده در این مساله شبکه عصبی در پایتون بیان شده است.
- ورودی از «مجموعه داده آموزش» (training dataset) گرفته، برخی تنظیمات بر مبنای وزن آنها انجام و سپس با استفاده از متدی که خروجی شبکه عصبی مصنوعی را محاسبه میکند انتقال داده میشوند.
- نرخ خطای بازگشت به عقب محاسبه میشود. در این شرایط، این مقدار تفاوت بین خروجی پیشبینی شده نورونها و خروجی مورد انتظار از مجموعه داده آموزش است.
- برپایه میزان خطای دریافت شده، تنظیمات وزن کوچکی با استفاده از «فرمول مشتق وزنی خطا» (Error Weighted Derivative Formula) انجام میشود.
- این فرآیند به طور دلخواه ۱۵۰۰ بار تکرار میشود (این مقدار منتخب نویسنده این مطلب است).
از تابع «T» برای ترانهادن ماتریس از موقعیت افقی به عمودی استفاده شده است. بنابراین، اعداد به صورت زیر ذخیره میشوند. در نهایت، وزن نورونها برای مجموعه داده آموزش فراهم شده بهینهسازی میشود. در نتیجه، اگر نورون ساخته شده تا درباره شرایط جدیدی فکر کند، که شبیه شرایط پیشین است، میتواند یک پیشبینی دقیق انجام دهد. این همان شیوهای است که بازشگت به عقب انجام میشود.
بستهبندی
در نهایت، کلاس شبکه عصبی در پایتون مقداردهی اولیه میشود و کدها اجرا خواهند شد.
در ادامه، کل کدهای لازم برای ساخت شبکه عصبی در پایتون آورده شده است.
خروجی حاصل از اجرای کد بالا به صورت زیر است.
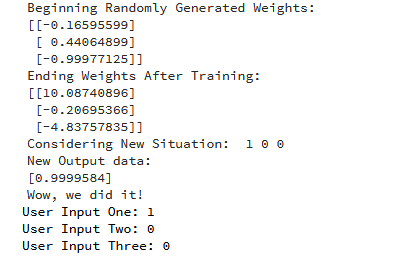
در این مطلب چگونگی ساخت یک شبکه عصبی در پایتون آموزش داده شد. نورون با تخصیص دادن وزنهای تصادفی به خودش آغاز به کار میکند و خود را با استفاده از «مثالهای آموزش» (Training Examples)، آموزش میدهد. در نتیجه، اگر با یک موقعیت جدید [1,0,0] به شکه عصبی ارائه شود، مقدار 0.9999584 را بازمیگرداند. همانطور که پیشتر و در بالا بیان شد، پاسخ مورد انتظار برای چنین شرایطی برابر با ۱ است و بنابراین پاسخ ارائه شده توسط شبکه عصبی بسیار نزدیک به این مقدار است. نباید فراموش کرد که تابع سیگموئید مقادیر خروجی بین ۰ و ۱ دارد.
البته، در اینجا تنها از شبکه تک نورونی برای انجام یک وظیفه ساده استفاده شده است. پرسشی که در این وهله به ذهن خطور میکند آن است که در صورت کنار هم قرار گرفتن چندین هزار شبکه عصبی چه اتفاقی میافتد و آیا با این کار میتوان چگونگی عملکرد ذهن انسان را به صورت ۱۰۰ درصدی شبیهسازی کرد؟
اگر نوشته بالا برای شما مفید بوده، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای هوش محاسباتی
- مجموعه آموزشهای شبکههای عصبی مصنوعی
- مجموعه آموزشهای آمار، احتمالات و دادهکاوی
- گنجینه آموزشهای برنامه نویسی پایتون (Python)
- معرفی منابع آموزش ویدئویی هوش مصنوعی به زبان فارسی و انگلیسی
^^













درود بر شما و تشکر از این مقاله عالی
فقط یک سئوال داشتم ، آیا این کد پایتون و نوشتن یک ANN از Backpropagation BP استفاده شده؟ ممنون
با سلام و احترام؛
بله. نرخ خطای «پس انتشار» در این پیادهسازی، محاسبه شده است.
از همراهی شما با مجله فرادرس، بسیار خوشنودیم.
سلام من یک پروژه انجام دادم با480هزاداده …حرفه ای نیستم و به زحمت تموم کردم ماشین بردارپشتیبان بود در مورد خرابی یا سالم بودن اعضای یک سازه یعنی دو کلاسه بود کارم…..حالا همین نتایج رو میخوام با نزدیکترین همسایگی یاmlp هم به دست بیارم و با هم قیاس کنم.به نظرتون نزدیکترین همسایگی با این تعداد داده کار میکنه یا به مشکل میخورم؟
با سلام
منظور شما از عبارت مقابل چیه ؟ ” اگر متغیر خروجی برابر با «x» است، مشتق آن برابر با «(x * (1-x» خواهد بود. ”
منظورتون مشتقه یا انتگرال ؟
با سلام؛
از همراهی شما با مجله فرادرس سپاسگزاریم. متن صحیح است . اگر خروجی تابع سیگموئید متغیر x باشد، میتوان مشتق «تابع سیگموئید» را با استفاده از این خروجی محاسبه کرد. آنچه در اینجا هم بیان شده، بر همین مفهوم دلالت دارد. یعنی، اگر خروجی تابع سیگموئید متغیر x باشد، مشتق خود تابع سیگموئید برابر با مقدار بیان شده است.
به بیان ریاضی، اگر فرض کنیم تابع سیگموئید x=1+e−y1 است، مشتق آن برابر با x˙=(1+e−y)2e−y خواهد بود. با کمی سادهسازی، خواهیم دید که x˙=x(1−x).
سپاسگزارم.
سلام
با تشکر از شما که بخاطر نوشتن این مطلب
اگه ممکنه مثال های بیشتری برای یادگیری بیشتر بنویسید