دامنه و برد توابع نمایی و لگاریتمی | به زبان ساده
توابع نمایی و لگاریتمی در ریاضیات و سایر علوم کاربردهای فراوانی دارند و به همین دلیل است که شناخت این توابع ضروری است. در این آموزش، با دامنه و برد توابع نمایی و لگاریتمی آشنا میشویم و با ارائه مثالهایی نحوه تعیین دامنه و برد توابع نمایی و لگاریتمی را بیان میکنیم.


تعریف دامنه یک تابع
دامنه تابعی مانند که به صورت عبارتی برحسب متغیر تعریف شده است، برابر است با مجموعه اعداد حقیقی متغیر که به ازای آنها مقدار تابع حقیقی است.
تعریف برد یک تابع
برد تابع برابر است با مجموعه مقادیری که به ازای قرار دادن مقادیر دامنه در متغیر برای تابع حاصل میشود.
تعیین دامنه و برد توابع نمایی و لگاریتمی
برای به دست آوردن دامنه و برد یک تابع ابتدا باید نوع آن تابع را تشخیص دهیم، زیرا توابع گوناگون از جمله توابع جبری، لگاریتمی، گویا، مثلثاتی و... دامنه و برد متفاوتی دارند. در ادامه این مطلب، به منظور آشنایی با نحوه تعیین دامنه و برد توابع نمایی و لگاریتمی مثالهایی را ارائه خواهیم کرد.
دامنه و برد تعدادی از توابع نمایی و لگاریتمی به شرح زیر است:
| برد | دامنه | تابع |
| ( ثابت) | ||
| ( و ثابت) |
نکته:
- اگر و باشد، آنگاه .
- اگر و باشد، آنگاه .

مثال های تعیین دامنه و برد توابع نمایی و لگاریتمی
در این بخش، چند مثال را از تعیین دامنه و برد توابع نمایی و لگاریتمی بیان میکنیم.
مثال اول دامنه و برد توابع نمایی و لگاریتمی
دامنه تابع را به دست آورید.
حل: طبق جدول فوق، اگر آرگومان یعنی مثبت باشد، مقادیر حقیقی خواهد بود:
بنابراین، دامنه این تابع برابر است با یا .
مثال دوم دامنه و برد توابع نمایی و لگاریتمی
دامنه تابع را بیابید.
حل: آرگومان این تابع، یعنی همواره بزرگتر از صفر و مثبت است. بنابراین، دامنه این تابع تمام اعداد حقیقی است، یعنی .
مثال سوم دامنه و برد توابع نمایی و لگاریتمی
دامنه تابع را تعیین کنید.
حل: برای اینکه حقیقی باشد، باید مثبت باشد:
مثال چهارم دامنه و برد توابع نمایی و لگاریتمی
دامنه تابع را مشخص کنید.
حل: مانند مثالهای قبل، آرگومان تابع باید مثبت باشد، یعنی:
همانطور که میدانیم، خروجی قدر مطلق، همواره یک مقدار مثبت است. بنابراین، دامنه این تابع برابر است با تمام اعداد حقیقی به جز .

مثال پنجم دامنه و برد توابع نمایی و لگاریتمی
دامنه تابع را به دست آورید.
حل: برای تعیین دامنه این تابع، باید نامعادله زیر را حل کنیم:
با تجزیه عبارت سمت چپ به صورت زیر، میتوان مجموعه جواب نامعادله را به دست آورد:
اگر این نامساوی را تعیین علامت کنیم، خواهیم داشت:
مثال ششم دامنه و برد توابع نمایی و لگاریتمی
برد تابع را به دست آورید.
حل: ابتدا را به صورت زیر مینویسیم:
سپس، تابع را برای حل میکنیم:
اگر باشد، یک مقدار حقیقی خواهد بود. بنابراین، همانطور که در نمودار زیر مشاهده میکنید، برد این تابع در بازه قرار دارد.
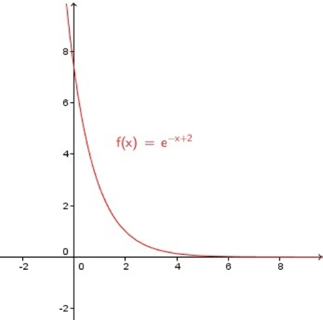
مثال هفتم دامنه و برد توابع نمایی و لگاریتمی
برد تابع را مشخص کنید.
حل: مانند مثال قبل، تابع را برای حل میکنیم:
مقدار در صورتی یک عدد حقیقی است که باشد. بنابراین، برد تابع مفروض خواهد بود.
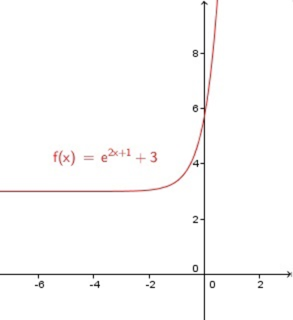
مثال هشتم دامنه و برد توابع نمایی و لگاریتمی
برد تابع را بیابید.
حل: برای به دست آوردن برد این تابع نمایی به صورت زیر عمل میکنیم:
این جوابها در صورتی حقیقی هستند که
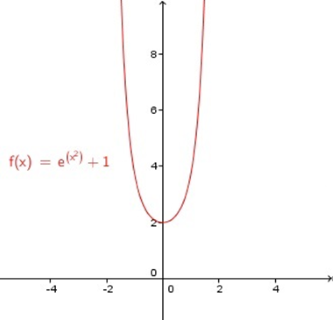
مثال نهم دامنه و برد توابع نمایی و لگاریتمی
برد تابع را تعیین کنید.
حل:
اگر آرگومان مثبت و عبارت زیر رادیکال مثبت یا صفر باشد، مقدار حقیقی خواهد بود. پس در اینجا دو شرط خواهیم داشت:
مجموعه جواب نامعادله اول به صورت زیر است:
و برای جواب معادله دوم، داریم:
بنابراین، برد تابع در بازه بسته قرار دارد.
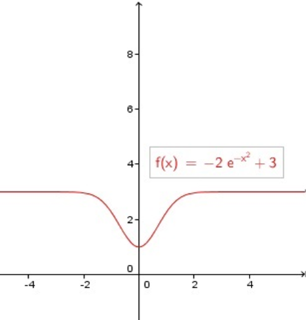
مثال دهم دامنه و برد توابع نمایی و لگاریتمی
دامنه تابع را تعیین کنید.
حل: این تابع، جذر یک عبارت لگاریتمی است. از طرف دیگر، آرگومان تابع لگاریتمی نیز یک تابع گویا است. از این رو، برای تعیین دامنه این تابع، ابتدا مقادیری از را که در تابع لگاریتمی صدق میکنند، مییابیم:
طرفین نامعادله را در ضرب میکنیم:
ریشههای عبارت سمت چپ نامعادله، برابر است با . در نتیجه، به ازای های بین و ، این عبارت منفی خواهد بود.
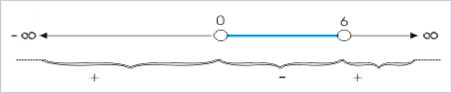
اکنون شرط عبارت زیر رادیکال که باید مثبت یا صفر باشد را اعمال کنیم:
واضح است که ریشههای عبارت سمت چپ نامعادله است. بنابراین، داریم:
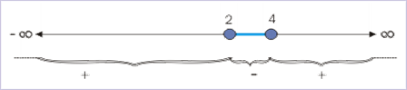
برای تعیین دامنه تابع مفروض کافی است اشتراک بازههای به دست آمده برای را به دست آوریم:
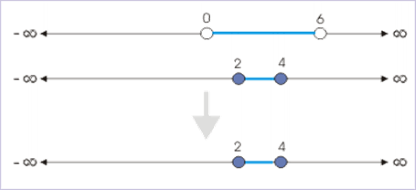
دامنه برابر است با .
مثال یازدهم دامنه و برد توابع نمایی و لگاریتمی
دامنه تابع را تعیین کنید.
حل: با توجه به اینکه این تابع شامل سه تابع لگاریتمی تودرتو با مبناهای مختلف است، ابتدا دامنه را مشخص میکنیم. آرگومان این تابع لگاریتمی باید مثبت باشد. یعنی .
برای حقیقی بودن عبارت نیز برقرار بودن شرط زیر لازم است:
با توجه به اینکه مبنای لگاریتم بزرگتر از صفر است (به نکتهای که در ابتدای مطلب ذکر شده است، رجوع کنید)، داریم:
برای اینکه تابع حقیقی باشد، باید مثبت باشد:
با ترکیب این سه بازه و به دست آورد اشتراک آنها خواهیم داشت:
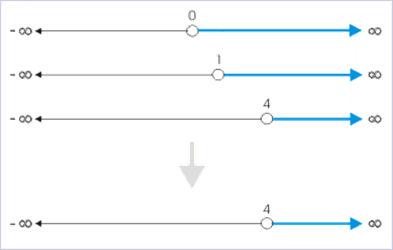
دامنه در بازه قرار دارد.
مثال دوازدهم دامنه و برد توابع نمایی و لگاریتمی
برد تابع را به دست آورید.
حل: آرگومان این تابع، یک تابع درجه دوم است، پس برای به دست آوردن برد تابع باید ابتدا مقدار اکسترمم آرگومان تابع لگاریتمی را به ازای مقادیری از که در دامنه تابع قرار دارد، تعیین کنیم. برای تعیین اکسترمم آرگومان تابع باید مشتق اول و دوم آن را به دست آوریم:
با توجه به اینکه مشتق دوم بزرگتر از صفر است، دارای یک مینیمم است. برای به دست آوردن نقطه مینیمم، کافی است مشتق اول را برابر با صفر قرار دهیم:
حال مقدار به دست آمده را در جایگذاری میکنیم تا مختصات نقطه مینیمم و در نتیجه برد تابع مشخص شود:
واضح است که برد تابع برابر است با .

مثال سیزدهم دامنه و برد توابع نمایی و لگاریتمی
دامنه تساوی را تعیین کنید.
حل: برای به دست آوردن دامنه کافی است از دو طرف تساوی لگاریتم بر مبنای بگیریم:
بنابراین، دامنه در بازه قرار دارد.
آزمون سنجش یادگیری
۱. دامنه یک تابع چگونه تعریف میشود و عدد عضو دامنه باید چه شرطی داشته باشد؟
هر عدد حقیقی بدون محدودیت عضو دامنه هر تابع است.
هر عددی که خروجی تابع صفر شود عضو دامنه است.
عددی که قرار دادن آن در تابع مقدار حقیقی بدهد عضو دامنه است.
اگر تابع فقط مثبت باشد عدد مربوطه عضو دامنه است.
دامنه تابع به مجموعهای از اعداد گفته میشود که برای آنها مقدار تابع معنیدار و حقیقی است. یعنی اگر با قرار دادن یک عدد بهجای متغیر تابع، خروجی عددی و بدون اشکال باشد، آن عدد عضو دامنه است. گفتهای مانند «هر عدد حقیقی بدون محدودیت» همیشه صحیح نیست، چون برخی توابع محدودیت دارند. همچنین عضویت عدد براساس مثبت بودن تابع یا صرفا خروجی صفر، شرط دامنه بودن نیست و فقط باید مقدار تابع برای آن معنیدار باشد.
۲. دامنه و برد یک تابع هرکدام چه مفهومی دارند و چگونه با یکدیگر متفاوتاند؟
دامنه تابع فقط شامل اعداد مثبت و برد فقط شامل اعداد منفی است.
دامنه مجموعه کلیه خروجیها و برد ورودیهای تابع است.
دامنه و برد هر دو فقط مبنای تابع را مشخص میکنند.
دامنه مجموعهای از ورودیهای مجاز و برد مجموعه خروجیهای تابع است.
عبارت «دامنه مجموعهای از ورودیهای مجاز و برد مجموعه خروجیهای تابع است» درست است، زیرا دامنه شامل تمام مقدارهایی است که میتوان به عنوان ورودی (متغیر) به تابع داد و تابع معنیدار باقی بماند. برد نیز شامل نتیجههایی است که میتوان از تابع با قرار دادن ورودیهای دامنه به دست آورد. «دامنه مجموعه کلیه خروجیها و برد ورودیهای تابع است» تعریف را به اشتباه جابجا کرده است. مورد «دامنه تابع فقط شامل اعداد مثبت و برد فقط شامل اعداد منفی است» کاملا نادرست است، چون دامنه و برد هر تابع میتواند بسته به نوع آن متفاوت باشد و به مثبت یا منفی بودن محدود نیست. عبارت «دامنه و برد هر دو فقط مبنای تابع را مشخص میکنند» نیز صحیح نیست و هیچ ارتباط مستقیمی با مبنای تابع ندارند.
۳. برای تعیین دامنه تابع لگاریتمی با آرگومان مرکب، چه روشی برای بهدست آوردن بازه مجاز x مناسب است؟
هر قسمت آرگومان را جداگانه مثبت فرض کنیم و نامساویها را همزمان حل کنیم.
صرفا مقدار کل آرگومان را نامساوی بگیریم و حل کنیم.
با جایگذاری اعداد دلخواه در آرگومان، بازه را تقریب بزنیم.
فقط بزرگترین جمله آرگومان را مثبت قرار دهیم و بررسی کنیم.
برای تعیین دامنه تابع لگاریتمی با آرگومان مرکب، باید تک تک بخشهای آرگومان را جداگانه مثبت در نظر گرفت و در نهایت شرایط را با هم ترکیب و همزمان حل کرد تا فقط اعدادی که باعث مثبت شدن کل آرگومان میشوند باقی بماند. این روش در بخش مثالها توضیح داده شده است. قرار دادن فقط یک جمله به جای هر بخش آرگومان یا صرفا نامساوی گرفتن برای کل عبارت بدون بررسی دقیق اجزاء کافی نیست. همچنین با جایگذاری دلخواه نمیشود بازه دقیق را تعیین کرد، بلکه حل همزمان نامساویها راه منطقی است.
۴. زمانی که تابع نمایی به صورت عمومی با یک ضریب و همچنین شیفت عمودی ترکیب میشود، تاثیر این دو تغییر بر روی برد تابع Exponential چه خواهد بود؟
هیچیک از تغییرات اثری بر برد تابع نمایی ندارند.
ضریب فقط دامنه را تغییر میدهد و شیفت فقط برد را جابهجا میکند.
تنها شیفت برد را تغییر میدهد و ضریب اثری ندارد.
ضریب و شیفت هر دو میتوانند سبب جابهجایی و کشیدگی برد شوند.
ضریب در تابع نمایی موجب کشیدگی یا فشرده شدن برد میشود و شیفت عمودی باعث جابهجایی بازه برد به بالا یا پایین خواهد شد. بنابراین هر دو، ضریب و شیفت، بازه خروجی تابع را تغییر میدهند. عبارت «ضریب و شیفت هر دو میتوانند سبب جابهجایی و کشیدگی برد شوند» درست است. سایر عبارات چون تنها یکی از این دو را موثر میدانند یا هر دو تغییر را بیاثر میدانند صحیح نیستند.
۵. در بررسی دامنه توابعی که شامل لگاریتم تو در تو و یا رادیکال در آرگومان هستند، چرا باید چند نامساوی تو در تو را حل کرده و اشتراک بازهها را پیدا کنیم؟
برای سادهتر شدن فرمول برد تابع اصلی
چون فقط باید آرگومان لگاریتم را مثبت در نظر گرفت.
زیرا تنها با این روش میتوان اکسترمم تابع را پیدا کرد.
زیرا هر شرط جداگانه فقط دامنه یکی از قسمتهای تابع را میدهد.
در توابع ترکیبی مثل زمانی که لگاریتمهای تو در تو یا رادیکال در آرگومان وجود دارد، هر بخش تابع یک شرط جدا برای اینکه مقدار حقیقی تولید شود میگذارد. برای بدست آوردن دامنه صحیح، بایستی همه این شروط را همزمان ارضا کنیم و همین باعث میشود چند نامساوی تو در تو حل شود و اشتراک بازهها به عنوان دامنه مجاز معرفی گردد. عبارت 'آرگومان لگاریتم را مثبت در نظر گرفتن' کافی نیست چون ممکن است شروط بیشتری از جمله مثبت بودن عبارت زیر رادیکال هم وجود داشته باشد. خروجی تابع (برد) یا اکسترمم تابع مربوط به دامنه نیست و ارتباطی با حل چند نامساوی ندارد.













تشکر
دمتون گرم عالی بود
Good
سلام.
سپاس از همراهیتان با مجله فرادرس.