حجم مکعب مستطیل چیست؟ – به زبان ساده + حل تمرین و مثال های متنوع
حجم مکعب مستطیل، اندازه فضایی است که بین سطحهای تشکیل دهنده آن قرار میگیرد. این اندازه از ضرب طول، عرض و ارتفاع مکعبمستطیل در یکدیگر بهدست میآید. فرمول حجم مکعبمستطیل، بسیار ساده است. با این وجود، به کاربردهای گسترده، آشنایی با آن از اهمیت بالایی دارد. در این آموزش از مجله فرادرس، به معرفی فرمول محاسبه حجم مکعب مستطیل به همراه حل چندین مثال متنوع و کاربردی میپردازیم.


مکعب مستطیل چیست؟
در مطلب «مکعب، منشور مربعی و مکعبمستطیل — به زبان ساده» از مجله فرادرس، مکعبمستطیل را تعریف کردیم. مکعب مستطیل، یکی از اشکال هندسی سهبعدی است که از شش وجه مسطح تشکیل میشود. تمام زاویههای داخلی مکعب مستطیل، برابر با ۹۰ درجه (زاویه قائمه) هستند.
بر اساس تعریف، این شکل را میتوان به عنوان یک منشور مستطیلی قائم الزاویه یا یک متوازیالسطوح مستطیلی در نظر گرفت. مکعب مربع، یکی از حالتهای خاص مکعب مستطیل است.
حجم مکعب مستطیل چیست؟
حجم، کمیتی است که میزان فضای سهبعدی بین یک یا چند سطح بسته را نمایش میدهد. به فضایی که مکعب مستطیل اشغال میکند، حجم مکعب مستطیل میگویند.
به عنوان مثال، یک محفظه شیشهای با شکل مکعب مستطیل را در نظر بگیرید. به اندازه فضای داخل این محفظه، حجم محفظه میگویند.

محفظه شیشهای آکواریوم بالا را میتوان با مایعاتی نظیر آب یا مواد دیگر پر کرد. میزان مادهای که درون این محفظه قرار میگیرد، به حجم آن (حجم مکعب مستطیل شیشهای) بستگی دارد. محاسبه حجم، یکی از مباحث مهم دنیای ریاضی است که در زندگی روزمره نیز مورد استفاده قرار میگیرد.
حجم مکعب مستطیل چگونه بدست می آید ؟
حجم مکعب مستطیل، از ضرب طول در عرض در ارتفاع بهدست میآید. تصویر زیر، اجزای یک مکعب مستطیل را نمایش میدهد. تفاوتی ندارد که کدام ضلع را به عنوان طول، عرض یا ارتفاع در نظر میگیرید، در هر صورت، مقدار به دست آمده برای حجم، یکسان خواهد بود.
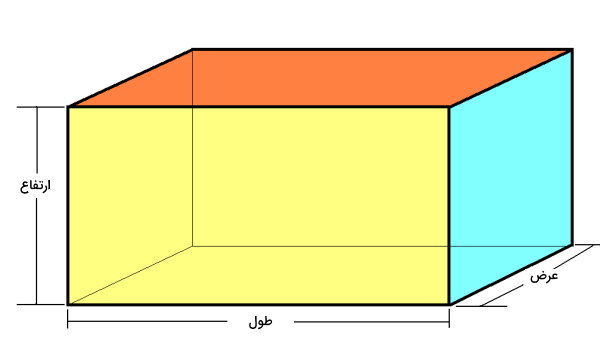
رابطه حجم مکعب مستطیل را میتوانیم به صورت زیر بنویسیم:
ارتفاع × عرض × طول = حجم مکعب مستطیل
مکعب مستطیل، یکی از انواع منشورهای قائم الزاویه است. به همین دلیل، حجم آن از رابطه زیر نیز محاسبه میشود:
ارتفاع × مساحت قاعده = حجم مکعب مستطیل
هر یک از وجههای مکعبمستطیل، یکی از قاعدههای آن محسوب میشود. ارتفاع نیز، ضلع عمود بر قاعده است. بنابراین، از ضرب مساحت یکی از وجههای مکعبمستطیل در اندازه ضلع عمود بر آن، حجم مکعبمستطیل بهدست میآید.
فرمول حجم مستطیل چیست؟
در ریاضیات، حجم را با حرف انگلیسی V (ابتدای کلمه Volume) نمایش میدهند. اگر طول، عرض و ارتفاع مکعب مستطیل را با حروف b ،a و c نمایش دهیم، رابطه جبری حجم مکعب مستطیل به شکل زیر نوشته میشود:
- V: حجم مکعبمستطیل
- a: طول مکعبمستطیل
- b: عرض مکعبمستطیل
- c: ارتفاع مکعبمستطیل
واحد حجم مکعب مستطیل چیست؟
حجم، معمولا با واحد لیتر یا متر مکعب بیان میشود. برای مکعبمستطیل نیز معمولا همین یکاها مورد استفاده قرار میگیرند. اگر یک مایع فضای مکعب مستطیل را اشغال کند، بهتر است واحد آن را با لیتر بیان کنیم. در صورت جامد یا گازی بودن فضای اشغال شده توسط مکعبمستطیل، از یکای متر مکعب یا واحدهای مشابه آن (فوت مکعب و غیره) استفاده میکنیم.
حل مثال های حجم مکعب مستطیل
به منظور آشنایی بیشتر و بهتر با نحوه محاسبه حجم مکعب مستطیل، در این بخش، به حل چند مثال کاربردی میپردازیم.
مثال ۱: محاسبه حجم کتاب مکعب مستطیل شکل
ابعاد سطح روی یک کتاب، برابر با ۹۰ در ۱۴۰ میلیمتر است. اگر ضخامت کتاب برابر با ۲۰ میلیمتر باشد، فضای اشغال شده توسط آن چقدر خواهد بود؟

کتابها، اجسامی به شکل مکعب مستطیل هستند. ابعاد سطح روی کتاب را به عنوان طول و عرض و ضخامت را نیز به عنوان ارتفاع در نظر میگیریم. بنابراین، داریم:
ارتفاع × عرض × طول = حجم کتاب
۲۰ × ۹۰ × ۱۴۰ = حجم کتاب
۲۵۲۰۰۰ = حجم کتاب
در نتیجه، حجم کتاب برابر با ۲۵۲۰۰۰ میلیمتر مکعب است.
مثال ۲: تبدیل واحد حجم مکعب مستطیل
حجم کتاب در مثال قبلی را به صورت سانتیمتر مکعب، متر مکعب و لیتر بیان کنید.
به منظور تبدیل واحد حجم، نکات زیر را در نظر بگیرید:
- هر ۱ متر مکعب، برابر با ۱۰۰۰ لیتر است.
- هر ۱ سانتیمتر مکعب، برابر با ۰/۰۰۰۰۰۱ متر مکعب است.
- هر ۱ میلیمتر مکعب، برابر با ۰/۰۰۱ سانتیمتر مکعب است.
در مثال قبلی، حجم کتاب برابر با ۲۵۲۰۰۰ میلیمتر مکعب به دست آمد. بر اساس نکات بالا، داریم:
۲۵۲ سانتیمتر مکعب = ۰/۰۰۱ × ۲۵۲۰۰۰ میلیمتر مکعب
۰/۰۰۰۲۵۲ متر مکعب = ۰/۰۰۰۰۰۱ × ۲۵۲ سانتیمتر مکعب
۰/۲۵۲ لیتر = ۱۰۰۰ × ۰/۰۰۰۲۵۲ متر مکعب
بیان حجم اجسام جامد با واحد لیتر، مرسوم نیست. در اینجا، فقط برای تمرین نحوه تبدیل واحدهای دیگر به این واحد، حجم کتاب را با لیتر بیان کردیم.
مثال ۳: تعیین ظرفیت کارتن کتاب به کمک رابطه حجم مکعب مستطیل
دانشآموزی در پایان سال تحصیلی، کتابهای درسی خود را در یک کارتن جمعآوری میکند. ابعاد کارتن، برابر با ۲۰ در ۲۵ در ۱۵ سانتیمترو ابعاد هر کتاب برابر با ۲۳ در ۱۶ در ۱ سانتیمتر است. با توجه به اطلاعات مسئله، به سوالات زیر پاسخ دهید:
- اگر دانشآموز، ۱۷ کتاب درسی داشته باشد، آیا میتواند تمام کتابها را درون کارتن قرار دهد؟
- حداکثر چند کتاب را میتوان درون کارتن قرار داد؟

برای اینکه ببینیم ۱۷ عدد کتاب درون کارتن جا میشود یا خیر، حجم کارت و مجموع کتابها را به دست میٰآوریم. حجم کارتن برابر است با:
۱۵ × ۲۵ × ۲۰ = حجم کارتن
۷۵۰۰ = حجم کارتن
کارتن، ۷۵۰۰ سانتیمتر مکعب ظرفیت دارد. حجم هر کتاب از رابطه زیر بهدست میآید:
۱ × ۱۶ × ۲۳ = حجم کتاب
۳۶۸ = حجم کتاب
حجم هر کتاب برابر با ۳۶۸ سانتیمتر مکعب است. بنابراین، حجم تمام کتابها برابر است با:
۳۶۸ × ۱۷ = حجم تمام کتابها
۶۲۵۶ = حجم تمام کتابها
حجم تمام کتابها (۶۲۵۶ سانتیمتر مکعب) از حجم کارت (۷۵۰۰ سانتیمتر مکعب) کمتر است. بنابراین، تمام کتابها درون کارتن جا میشوند.
به منظور تعیین حداکثر تعداد کتابهای قابل جمعآوری درون کارتن، باید حجم کارتن را بر حجم هر کتاب تقسیم کنیم:
۳۶۸ ÷ ۷۵۰۰ = ظرفیت کارتن به ازای کتاب
۲۰/۳۸ = ظرفیت کارتن به ازای کتاب
حداکثر ۲۰/۳۸ کتاب درون کارتن جای میگیرند. البته، از آنجایی که تعداد کتابها، همواره یک عدد صحیح غیر منفی (۱، ۲، ۳ و ...) است، میتوانیم بگوییم حداکثر ۲۰ کتاب درون کارت جا میشود.
مثال ۴: محاسبه حجم مکعب مستطیل به لیتر
ابعاد یک مکعبمستطیل برابر با ۸، ۵ و ۴ متر است. حجم مکعب مستطیل را بر حسب لیتر محاسبه کنید.
حجم مکعبمستطیل برابر است با:
ارتفاع × عرض × طول = حجم مکعبمستطیل
۴ × ۵ × ۸ = حجم مکعبمستطیل
۱۶۰ = حجم مکعبمستطیل
حجم مکعبمستطیل برابر با ۱۶۰ متر مکعب است. در مثال ۲ گفتیم که هر ۱ متر مکعب، برابر با ۱۰۰۰ لیتر میشود. بنابراین، داریم:
۱۶۰۰۰۰ لیتر = ۱۰۰۰ × ۱۶۰ متر مکعب
مثال ۵: تعیین ارتفاع مکعب مستطیل
مساحت قاعده یک مکعبمستطیل برابر با ۹۹ سانتیمتر مربع و حجم آن برابر با ۶۹۳ سانتیمتر مکعب است. ارتفاع مکعبمستطیل را به دست بیاورید.
رابطه حجم مکعبمستطیل به صورت زیر نوشته میشود:
ارتفاع × عرض × طول = حجم مکعبمستطیل
حاصل عبارت «طول × عرض»، همان مساحت قاعد است. مقدار مساحت قاعده و حجم را درون رابطه بالا قرار میدهیم:
ارتفاع × ۹۹ = ۶۹۳
۹۹ ÷ ۶۹۳ = ارتفاع
۷ = ارتفاع
ارتفاع مکعب مستطیل برابر با ۷ متر است.
مثال ۶: تعیین تعداد مکعب مربع واحد درون مکعب مستطیل
یک مکعب مستطیلی به ابعاد ۱۲، ۳۰ و ۲۵ را در نظر بگیرید. اگر بخواهیم این مکعب مستطیل را با چندین مکعب مربع به ابعاد ۱ واحد پر کنیم، تعداد مکعب مربعهای درون مکعبمستطیل چقدر خواهد بود؟

حجم مکعبمستطیل برابر است با:
۲۵ × ۳۰ × ۱۲ = حجم مکعبمستطیل
۹۰۰۰ = حجم مکعبمستطیل
حجم مکعب مستطیل برابر با ۹۰۰۰ واحد حجم است. حجم هر مکعب، از رابطه زیر بهدست میآید:
۱ × ۱ × ۱ = حجم مکعبمربع
۱ = حجم مکعبمربع
حجم هر مکعبمربع برابر با ۱ واحد حجم است. بنابراین، تعداد مکعبمربعهای درون مکعبمستطیل برابر میشود با:
۱ ÷ ۹۰۰۰ = تعداد مکعبمربعها
۹۰۰۰ = تعداد مکعبمربعها
۹۰۰۰ مکعب مربع درون مکعبمستطیل قرار میگیرد.
مثال ۷: تعیین حداکثر تعداد مکعب مربع درون مکعب مستطیل
ابعاد یک مکعب مستطیل برابر با ۴/۵، ۳ و ۱/۷ است. چند مکعب مربع به ابعاد ۰/۷ درون این مکعب مستطیل جا میشود؟
حجم مکعبمستطیل و مکعبمربع را به دست میآوریم:
۲۲/۹۵ = ۱/۷ × ۳ × ۴/۵ = حجم مکعبمستطیل
۰/۳۴۳ = ۰/۷ × ۰/۷ × ۰/۷ = حجم مکعبمربع
برای به دست آوردن تعداد مکعبهای قابل جایگذاری درون مکعبمستطیل، اعداد بالا بر هم تقسیم میکنیم:
۶۶/۹۱ = ۰/۳۴۳ ÷ ۲۲/۹۵
بر اساس نتیجه تقسیم بالا، حداکثر ۶۶ مکعبمربع درون مکعب مستطیل جا میشود.
مثال ۸: تعیین ابعاد مکعب مربع
مکعب مستطیلی به ابعاد ۱۲، ۹ و ۶ سانتیمتر را با ۲۴ عدد مکعب مربع کاملا پر کردهایم. مساحت هر وجه مکعب مربع را به دست بیاورید.
مکعبمستطیل، با ۲۴ عدد مکعبمربع پر شده است. بنابراین، حجم ۲۴ مکعبمربع با حجم مکعبمستطیل برابری میکند. به عبارت دیگر:
حجم مکعبمربع × ۲۴ = ۶ × ۹ × ۱۲
حجم مکعبمربع × ۲۴ = ۶۴۸
۲۴ ÷ ۶۴۸ = حجم مکعبمربع
۲۷ = حجم مکعبمربع
حجم مکعبمربع برابر با ۲۷ سانتیمتر مربع است. این عدد از ضرب اندازه طول، عرض و ارتفاع مکعبمربع بهدست میآید. از آنجایی که تمام این اندازهها در مکعبمربع با هم برابر هستند، رابطه حجم این شکل را میتوانیم به صورت زیر بنویسیم:
اندازه ضلع × اندازه ضلع × اندازه ضلع = حجم مکعبمربع
۳اندازه ضلع = حجم مکعبمربع
۳اندازه ضلع = ۲۷
اندازه هر ضلع مکعبمربع برابر با ۳ سانتیمتر است؛ چراکه:
۲۷ = ۳ × ۳ × ۳
مثال ۹: محاسبه ابعاد خاک حفاری
چاهی به عمق ۲۰ متر و شعاع ۰/۵ متر را حفر کردهایم. هنگام خروج خاک از درون چاه، حجم آن ۱/۳ برابر میشود. این خاک را پس از حفاری، به محلی با ابعاد ۳ در ۵ متر میریزیم. ارتفاع خاک جمعآوری شده در بیرون چاه را حساب کنید. (عدد پی را برابر با ۳ در نظر بگیرید.)
چاه، شبیه به یک استوانه است. حجم استوانه، از ضرب مساحت مقطع دایرهای در ارتفاع بهدست میآید:
ارتفاع × مساحت دایره = حجم استوانه
ارتفاع × شعاع × شعاع × عدد پی = حجم استوانه
۲۰ × ۰/۵ × ۰/۵ × ۳ = حجم استوانه
۱۵ = حجم استوانه
حجم خاک خارج شده، بر اثر تورم، ۱/۵ برابر میشود:
۱۵× ۱/۳ = حجم خاک متورم
۱۹/۵ = حجم خاک متورم
حجم خاک در محل جمعآوری برابر است با:
حجم خاک متورم = ارتفاع × عرض × طول = حجم خاک جمعآوری شده
۱۹/۵ = ارتفاع × ۵ × ۳
۱۹/۵ = ارتفاع × ۱۵
۱۵ ÷ ۱۹/۵ = ارتفاع
۱/۳ = ارتفاع
بنابراین، ارتفاع خاک جمعآوری شده در محل مورد نظر تا ۱/۳ متر میرسد.
مثال ۱۰: تعیین مدت زمان پر شدن آکواریوم
یک آکواریوم به ابعاد ۳۰ در ۴۶ در ۹۱ سانتیمتر را در نظر بگیرید. اگر لوله آبی را با نرخ جریان ۲۶ لیتر بر دقیقه، به این آکواریوم وصل کنیم، پر شدن تقریبی آن چه مقدار زمان میبرد؟
برای محاسبه مدت زمان پر شدن آکواریوم، به حجم آن نیاز داریم. این حجم از رابطه زیر محاسبه میشود:
۹۱ × ۴۶ × ۳۰ = حجم آکواریوم
۱۲۵۵۸۰ = حجم آکواریوم
نرخ جریان آب با واحد لیتر بر دقیقه داده شده است. بنابراین باید حجم بالا را از سانتیمتر مکعب به لیتر تبدیل کنیم:
۱۲۵/۵۸ لیتر = ۰/۰۰۱ × ۱۲۵۵۸۰ سانتیمتر مکعب
حجم آکواریم برابر با ۱۲۵/۵۸ لیتر استو در هر دقیقه نیز، ۲۶ لیتر آب وارد آکواریوم میشود. بنابراین، مدت زمان پر شدن تقریبی آن برابر است با:
۲۶ ÷ ۱۲۵/۵۸ = زمان پر شدن آکواریوم
۴/۸۳ = زمان پر شدن آکواریوم
بنابراین، بین ۴ تا ۵ دقیقه طول میکشد تا آکواریوم به اندازه کافی پر شود.
مثال ۱۱: محاسبه درصد تغییرات حجم مکعب مستطیل
حجم یک محفظه پر از آب با قاعده ۱ در ۰/۷ متر برابر با ۰/۴۲ متر مکعب است. با گذشت زمان، ارتفاع آب در این محفظه به ۴۰ سانتیمتر میرسد. درصد تغییرات حجم آب موجود در محفظه را حساب کنید.
هنگامی که ارتفاع آب در محفظه به ۴۰ سانتیمتر (۰/۴ متر) میرسد، حجم ثانویه آب برابر میشود با:
۰/۴ × ۰/۷ × ۱ = حجم ثانویه آب
۰/۲۸ = حجم ثانویه آب
اختلاف حجم اولیه و ثانویه آب برابر است با:
۰/۲۸ - ۰/۴۲ = میزان کاهش حجم
۰/۱۴ = میزان کاهش حجم
نسبت تغییرات حجم از تقسیم میزان کاهش حجم بر حجم اولیه بهدست میآید:
۰/۴۲ ÷ ۰/۱۴ = نسبت تغییرات حجم
۰/۳۳ = نسبت تغییرات حجم
اگر عدد بالا را در عدد ۱۰۰ ضرب کنیم، درصد تغییرات حجم مشخص میشود:
۰/۳۳ × ۱۰۰ = درصد تغییرات حجم
۳۳ = درصد تغییرات حجم
سوالات متداول در رابطه با حجم مکعب مستطیل
در این مطلب از مجله فرادرس با چگونگی محاسبه حجم مکعبمستطیل آشنا شدیم. در این بخش، به برخی از سوالات پرتکرار در رابطه با حجم مکعب مستطیل پاسخ میدهیم.
حجم مکعب مستطیل برابر با چیست؟
حجم مکعب مستطیل برابر با حاصلضرب طول در عرض در ارتفاع است.
رابطه جبری حجم مکعب مستطیل چیست؟
عبارت جبری حجم مکعبمستطیل برابر با V=abc است.
یکای حجم مکعب مستطیل چیست؟
لیتر، متر مکعب، فوت مکعب و غیره، از واحدهای متداول برای بیان میزان حجم مکعبمستطیل هستند.
حجم مکعب مستطیل به لیتر چیست؟
حجم مکعبمستطیل به لیتر، ۰/۰۰۱ حجم مکعب مستطیل به متر مکعب است.
حجم و مساحت مکعب مستطیل چه تفاوتی دارند ؟
حجم، یک اندازه سهبعدی و مساحت، یک اندازه دوبعدی است. مساحت مکعب مستطیل، جمع اندازه روی وجوه تشکیل دهنده آن را نمایش میدهد. در صورتی که حجم مکعبمستطیل، بیانگر فضای محدود به این وجوه است.
مطلبی که در بالا مطالعه کردید بخشی از مجموعه مطالب «آموزش های بدست آوردن محیط و مساحت مستطیل + حل تمرین و تمامی فرمول ها» است. در ادامه، میتوانید فهرست این مطالب را ببینید:
- مستطیل چیست ؟ — تعریف و مفاهیم به زبان ساده
- طول و عرض مستطیل چیست و چگونه بدست می آید ؟ + حل تمرین و مثال
- قطر مستطیل چیست و چه خواصی دارد؟ — فرمول های محاسبه + حل مثال
- محیط مستطیل چگونه بدست می آید؟ + حل تمرین و مثال
- مساحت مستطیل به زبان ساده + حل تمرین
- حجم مکعب مستطیل چیست ؟ — به زبان ساده + حل تمرین و مثال های متنوع(همین مطلب)
- رابطه محیط و مساحت مستطیل — معرفی فرمول ها + حل تمرین و مثال
- فرمول محیط مستطیل چیست ؟ — به زبان ساده + حل مثال
- فرمول مساحت مستطیل چیست ؟ — به زبان ساده + حل مثال
- محیط مستطیل به صورت جبری — فرمول های محیط مستطیل + حل تمرین و مثال
- مساحت مستطیل به صورت جبری — فرمول های ریاضی + حل مثال
- محیط مستطیل کسری چگونه بدست می آید ؟ + حل تمرین و مثال
- مساحت مستطیل کسری چگونه بدست می آید ؟ — حل تمرین و مثال












