تابع زتای ریمان – از صفر تا صد
پیشتر در وبلاگ فرادرس تابع گاما و تابع بتا را معرفی کرده و ویژگیهای آن را نیز توضیح دادیم. به همین دلیل در این مطلب قصد داریم تا در مورد نوع جدیدی از توابع ریاضی بحث کرده که میتوان آنها را بر حسب توابع بتا و گاما نیز بیان کرد. این تابع تحت عنوان تابع زتای ریمان شناخته میشود.


تابع زتای ریمان
تابع زتای ریمان یا تابع اویلر ریمان ، تابعی از مقدار مختلط است که از نظر تحلیلی میتوان آن را مطابق با رابطه زیر در نظر گرفت.
شکل زیر نمونهای از کانتور توزیع تابع زتا را نشان میدهد.
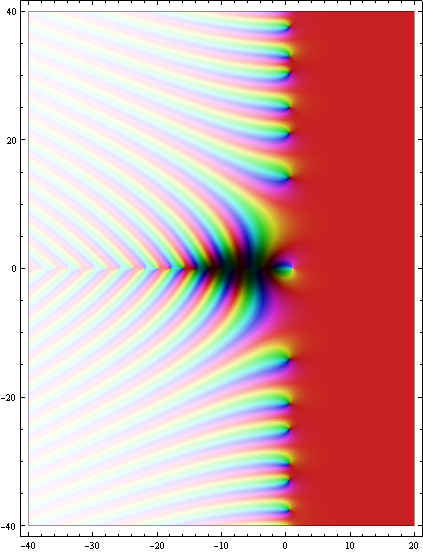
در شکل فوق رنگهای مشکی نشاندهنده مقادیر نزدیک به صفر بوده نوارهای سفید در مقادیر هستند که نشاندهنده قطبهای تابع است.
جمع فوق زمانی همگرا است که بخش حقیقی بیشتر از باشد. البته شکل عمومیتر این تابع به ازای تمامی مقادیر را در ادامه ارائه خواهیم داد. تابع زتا را میتوان با استفاده از انتگرال زیر بیان کرد:
همانطور که مشاهده میکنید در تابع زتا از تابع گاما نیز استفاده شده است. در گذشته نیز بیان شد که تابع گاما را میتوان با استفاده از انتگرال زیر بدست آورد:
در شرایطی ویژه که بخش حقیقی بیشتر از ۱ باشد، همواره همگرا است. در این حالت تابع را میتوان در قالب سری بینهایت زیر نیز بیان کرد:
تابع فوق به ازای مقادیر ، تابعی تحلیلی محسوب میشود. در ابتدا لئونارد اویلر در سال ۱۷۴۰ این تابع را به ازای مقادیر مثبت و طبیعی مطالعه کرد؛ پس از آن چبیشف آن را به ازای توسعه داد. البته سری فوق را میتوان نمونهای از یک سری دیریکله نیز در نظر گرفت. بدیهی است که این سری به ازای مقادیری از همگرا است و به ازای دیگر مقادیر واگرا خواهد بود. به ازای مقدار ، سری بهصورت هارمونیک است که مقدار آن به میل میکند. در حقیقت میتوان گفت:
بنابراین میتوان گفت در تمامی نقاط به جز ، تابع زتا تحلیلی است و مقدار باقیمانده آن نیز در این نقطه برابر با ۱ است. به ازای هر مقدار مثبت و طبیعی همچون میتوان رابطه زیر را بیان کرد:
در رابطه ارائه شده در بالا، نشاندهنده عدد برنولی ام است. به ازای مقادیر مثبت و فرد، چنین رابطه مشخصی وجود ندارد. برای مقادیر منفی یا صفر که فرد نیز هستند میتوان رابطه زیر را بیان کرد:
توجه داشته که مقدار اولیه برابر است با:
در ادامه مهمترین مقادیر این تابع ارائه شدهاند.
فرمول ضربی اویلر
ارتباط بین تابع زتا و اعداد اول توسط اویلر کشف شد. او این ارتباط را با اثبات رابطه زیر بدست آورد.
با استفاده از تعریف تابع زتا، سمت چپ را میتوان قرار داده و ضرب بینهایت ارائه شده در سمت راست نیز که روی اعداد اول توسعه پیدا کرده را میتوان بهصورت زیر بیان کرد (به عبارت زیر ضرب اویلر نیز گفته میشود):
هر دو سمت ضرب اویلر به ازای مقادیر همگرا است.
معادله ریمان
تابع زتا، معادله زیر را ارضا میکند.
توجه داشته باشید که در معادله فوق، نشاندهنده تابع گاما است. این برابری تابع روی تمامی صفحه مختلط برقرار است. معادله فوق، مقادیر تابع زتای ریمان در نقاط و و همچنین اعداد زوج مثبت را نیز با اعداد فرد منفی مرتبط میکند. با توجه به صفرهای عبارت سینوسی، معادله عملگر نشان میدهد که دارای صفری ساده در اعداد زوج منفی بوده که آن را تحت عنوان صفرهای جزئی میشناسند. هنگامی که یک عدد زوج مثبت باشد، حاصلضرب در سمت راست غیر صفر است؛ چراکه دارای یک قطب ساده بوده که صفر ساده ترم سینوس را حذف میکند.
معادله ریمان در سال ۱۸۵۹ در مقالهای با عنوان «تعداد اعداد اول موجودِ کمتر از مقداری داده شده» منتشر شد. البته در حدود ۱۰۰ سال عقبتر، در سال ۱۷۴۹ نیز اویلر رابطهای مشابه را بدست آورده بود. این رابطه مشابه تحت عنوان معادله دیریکله-اتا شناخته میشود. معادله مذکور بهصورت زیر است.
این معادله بهطور اتفاقی معادلهای را به ما میدهد که با استفاده از آن میتوان تابع را به ازای مقادیر بدست آورد. این معادله برابر است با:
در رابطه فوق سری به ازای نیمه بزرگتر صفحه () همگرا است. ریمان همچنین نسخه متقارن معادلهاش را یافت. شکل معادله مذکور بهصورت زیر بدست آمد.
با توجه به معادله فوق رابطه زیر نیز برقرار است.
با توجه به معادله ریمان (معادله سینوسی ارائه شده در بالا) میتوان گفت که مقادیر زتا در ۴-،۲- و دیگر ضرایب صحیح برابر با صفر است. توجه داشته باشید که این ریشهها، ریشههای معمولی یا همان تکراری نامیده میشوند. دلیل تکراری نامیده شدن این است که این مقادیر ریشههای ترم سینوسی موجود در رابطه نیز هستند. دیگر صفرهای معادله در نظریه اعداد از اهمیت بیشتری برخوردار هستند. مقادیر محاسبه شده نشان میدهند که پاسخهای غیرمعمول روی نوار زیر قرار میگیرند.
به این نوار، نوار بحرانی گفته میشود. حدس ریمان نیز که به عنوان یکی از بزرگترین مسائل حلنشده در ریاضی تلقی میشود، بیان میکند که بخش حقیقی صفرهای غیرمعمول معادله ریمان برابر با است. در نظریه تابع زتای ریمان، به مجموعه نقاط ، خط بحرانی گفته میشود. البته این خط را در مطلبی تحت عنوان تابع بیشتر توضیح خواهیم داد.
در صورت علاقهمندی به مباحث مرتبط در زمینه ریاضی و آمار آموزشهای زیر نیز به شما پیشنهاد میشوند:
^^











اگر اعداد حقیقی یاموهومی بعداز خط بحرانی تابع را صفر کند من میتوانم ثابت کنم تا بی نهایت اعداد در این تابع صدق کند
با سلام خدمت شما؛
برای استفاده از صفرها خارج از خط بحرانی دقیقا باید مشخص شود آن صفرها کجا هستند و چه ساختاری دارند. اثبات اینکه بینهایت صفر در تابع زتا صدق میکنند (یعنی صفر هستند) قبلا انجام شده، اما اینکه همه آنها روی خط بحرانی هستند، هنوز اثبات نشده است.
از همراهی شما با مجله فرادرس سپاسگزاریم.
تو فرمول تابعی زتا به ازای s های زوج مثبت، دلیل اینکه ترم سینوس صفر نمیشه گفتید چون با قطب ساده گاما، حذف میشه. این رو اگه توضیح بدید ممنون میشم
با سلام خدمت شما؛
این عبارت به این معناست که اگرچه ترم سینوس به سمت صفر میل میکند، اما این میل به صفر دقیقا توسط میل به بینهایت ترم گاما (به دلیل قطب ساده) خنثی میشود.
از همراهی شما با مجله فرادرس سپاسگزاریم.
سلام ،
گفته نشد که مقدار تابع زتا بنابه فرضیه ریمان که در ان ادعا می شود در نقطه x=1/2 و بین صفر و یک ، برابر با صفر است ، چرا در بالا برابر با ؛
1.46-نوشته شده و نه صفر ؟!
متشکرم
با سلام و وقت بخیر؛
تابع زتای ریمان، در نقاط مختلف مقادیر متفاوتی دارد. فرضیه ریمان ادعا میکند که صفرهای غیر بدیهی این تابع در خط بحرانی Re(s)=1/2 قرار دارند. به عبارت دیگر، اگر فرضیه ریمان صحیح باشد، تمامی صفرهای غیربدیهی تابع زتا باید دارای قسمت حقیقی برابر با 1/2 باشند. تابع زتای ریمان دارای دو نوع صفر است: صفرهای بدیهی (که در اعداد منفی زوج قرار دارند) و صفرهای نابدیهی (که بر روی خط بحرانی قرار دارند). فرضیه ریمان به بررسی مکان صفرهای نابدیهی میپردازد و هنوز اثبات نشده که این صفرها فقط در خط بحرانی واقع شدهاند. محاسبات عددی نشان دادهاند که تا کنون همه صفرهای نابدیهی محاسبه شده بر روی خط بحرانی قرار دارند اما این موضوع برای تمامی صفرها هنوز اثبات نشده است. در نتیجه، مقدار تابع زتای ریمان در نقطه x=1/2 و بین 0 و 1، برابر با 0.0i-1.46 است. عدد 1.46-، مقدار حقیقی این تابع را نشان میدهد.
از همراهی شما با مجله فرادرس سپاسگزاریم