در آموزشهای قبلی مجله فرادرس، درباره انتگرال و روشهای محاسبه آن بحث کردیم. در این آموزشها، مباحثی مانند انتگرال توابع مثلثاتی ، انتگرالگیری جزء به جزء ، انتگرال دوگانه و انتگرال سهگانه را معرفی کردیم. در این آموزش، روش محاسبه انتگرال توابع گنگ را با ارائه مثالهای گوناگون بررسی خواهیم کرد.
محتوای این مطلب جهت یادگیری بهتر و سریعتر آن، در انتهای متن به صورت ویدیویی نیز ارائه شده است.
برای انتگرالگیری از یک تابع گنگ شامل x m n {x^{\large\frac{m}{n}\normalsize}} x n m تغییر متغیر u = x 1 n u = {x^{\large\frac{1}{n}\normalsize}} u = x n 1 x x x u = x 1 n u = {x^{\large\frac{1}{n}\normalsize}} u = x n 1 n n n
برای عباراتی بهفرم a x + b c x + d n \sqrt[\large n\normalsize]{{\large\frac{{ax + b}}{{cx + d}}\normalsize}} n c x + d a x + b u = ( a x + b c x + d ) 1 n u = {\left( {\large\frac{{ax + b}}{{cx + d}}\normalsize} \right)^{\large\frac{1}{n}\normalsize}} u = ( c x + d a x + b ) n 1
مثالها
در ادامه، برای درک بهتر انتگرالگیری از توابع گنگ، چند مثال را بررسی میکنیم.
مثال 1
انتگرال ∫ x + 9 x d x {\large\int\normalsize} {{\large\frac{{\sqrt {x + 9} }}{x}\normalsize} dx} ∫ x x + 9 d x
حل: ابتدا، از تغییر متغیر زیر استفاده میکنیم:
u = ( x + 9 ) 1 2 , ⇒ x + 9 = u 2 , ⇒ x = u 2 – 9 , d x = 2 u d u . \large {u = { \left( { x + 9} \right) ^ { \large \frac { 1 }{ 2 } \normalsize}},\;\;}\Rightarrow { x + 9 = { u ^ 2 },\;\; }\\ \large \Rightarrow { x = { u ^ 2 } – 9,\;\;\;} \kern-0.3pt{ d x = 2 u d u . } u = ( x + 9 ) 2 1 , ⇒ x + 9 = u 2 , ⇒ x = u 2 –9 , d x = 2 u d u .
در نتیجه، داریم:
∫ x + 9 x d x = ∫ u u 2 – 9 ⋅ 2 u d u = 2 ∫ u 2 u 2 – 9 d u = 2 ∫ u 2 – 9 + 9 u 2 – 9 d u = 2 ∫ ( 1 + 9 u 2 – 9 ) d u = 2 ∫ d u + 18 ∫ d u u 2 – 3 2 = 2 u + 18 ⋅ 1 6 ln ∣ u – 3 u + 3 ∣ + C = 2 x + 9 + 3 ln ∣ x + 9 – 3 x + 9 + 3 ∣ + C . \large {\int {\frac { { \sqrt { x + 9 } } } { x } d x } } = {\int {\frac { u } { { { u ^ 2 } – 9 } } \cdot 2 u d u } } \\ \large = { 2 \int {\frac { { { u ^ 2 } } } { { { u ^ 2 } – 9 } } d u } } = {2\int {\frac{{{ u^ 2 } – 9 + 9 }} {{ { u ^ 2 } – 9 } }d u} } \\ \large = { 2 \int { \left( { 1 + \frac{ 9} {{ { u ^2 } – 9 } } } \right) d u } } = { 2\int { d u } + 18\int {\frac{{du } } { {{ u ^ 2} – {3 ^2 } } } } } \\ \large = { { 2 u + 18 \cdot \frac{ 1} { 6} \ln \left| {\frac{{ u – 3 }} { { u + 3 } } } \right| } + { C }} = { { 2\sqrt { x + 9} }+{ 3 \ln \left| {\frac{{\sqrt { x + 9} – 3}}{{\sqrt {x + 9} + 3}}} \right| }+{ C.}} ∫ x x + 9 d x = ∫ u 2 –9 u ⋅ 2 u d u = 2 ∫ u 2 –9 u 2 d u = 2 ∫ u 2 –9 u 2 –9 + 9 d u = 2 ∫ ( 1 + u 2 –9 9 ) d u = 2 ∫ d u + 18 ∫ u 2 – 3 2 d u = 2 u + 18 ⋅ 6 1 ln u + 3 u –3 + C = 2 x + 9 + 3 ln x + 9 + 3 x + 9 –3 + C .
مثال ۲
انتگرال ∫ x – 1 x + 1 d x \int {{\large\frac{{\sqrt x – 1}}{{\sqrt x + 1}}\normalsize} dx} ∫ x + 1 x –1 d x
حل: ابتدا از تغییر متغیر زیر استفاده میکنیم:
x = u , ⇒ x = u 2 , d x = 2 u d u . \large { \sqrt x = u ,\;\;} \Rightarrow { x = { u ^ 2 } ,\;\;\;}\;\kern-0.3pt { d x = 2 u d u . } x = u , ⇒ x = u 2 , d x = 2 u d u .
انتگرال را I I I
I = ∫ x – 1 x + 1 d x = ∫ u – 1 u + 1 2 u d u = 2 ∫ u 2 – u u + 1 d u . \large { I = \int { \frac { { \sqrt x – 1 } } { { \sqrt x + 1 } } d x } } = { \int {\frac { { u – 1 } } { { u + 1 } } 2 u d u } } = { 2 \int { \frac { { {u ^ 2 } – u } } { { u + 1 } } d u } . } I = ∫ x + 1 x –1 d x = ∫ u + 1 u –1 2 u d u = 2 ∫ u + 1 u 2 – u d u .
تقسیم کسر را انجام میدهیم:
u 2 – u u + 1 = u – 2 + 2 u + 1 . \large { \frac { { { u ^ 2 } – u } } { { u + 1 } } } = { u – 2 } + { \frac { 2 } { { u + 1 } } . } u + 1 u 2 – u = u –2 + u + 1 2 .
در نتیجه، داریم:
I = 2 ∫ ( u – 2 + 2 u + 1 ) d u = 2 ∫ u d u − 4 ∫ d u + 4 ∫ d u u + 1 = 2 u 2 2 – 4 u + 4 ln ∣ u + 1 ∣ + C = x – 4 x + 4 ln ∣ x + 1 ∣ + C . \large {I }={ 2\int {\left( {u – 2 + \frac{2}{{u + 1}}} \right)du} } \\ \large = { { 2 \int { u d u} }-{ 4\int {du} }+{ 4\int {\frac{{du}}{{u + 1}}} }} \\ \large = {{\frac { { 2 { u ^ 2 } } } { 2} – 4 u } + { 4 \ln \left| {u + 1} \right| } + { C } } \\ \large = { { x – 4 \sqrt x } + { 4\ln \left| {\sqrt x + 1} \right| } + { C . } } I = 2 ∫ ( u –2 + u + 1 2 ) d u = 2 ∫ u d u − 4 ∫ d u + 4 ∫ u + 1 d u = 2 2 u 2 –4 u + 4 ln ∣ u + 1 ∣ + C = x –4 x + 4 ln x + 1 + C .
مثال ۳
انتگرال ∫ d x x + x 3 {\large\int\normalsize} {\large\frac{{dx}}{{x + \sqrt[3]{x}}}\normalsize} ∫ x + 3 x d x
حل: انتگرال بهصورت زیر است:
I = ∫ d x x + x 3 = ∫ d x x + x 1 3 . \large { I = \int {\frac { { d x } } { { x + \sqrt[\large 3\normalsize] { x } } } } } = {\int {\frac{{dx}} {{ x + {x ^ { \large\frac {1}{3} \normalsize} } } } } . } I = ∫ x + 3 x d x = ∫ x + x 3 1 d x .
از آنجایی که کوچکترین مضرب مشترک (LCM) مخرج توان کسرها برابر با n = LCM ( 1 , 3 ) = 3 n = \text{LCM}\left({1,3}\right) = 3 n = LCM ( 1 , 3 ) = 3
u = x 1 3 , ⇒ x = u 3 , d x = 3 u 2 d u . \large {u = { x ^ { \large \frac { 1 } { 3 } \normalsize } } ,\;\;} \Rightarrow { x = { u ^3},\;\;\;}\kern-0.3pt{ d x = 3 { u ^ 2 } d u . } u = x 3 1 , ⇒ x = u 3 , d x = 3 u 2 d u .
بنابراین، داریم:
I = ∫ d x x + x 1 3 = ∫ 3 u 2 d u u 3 + ( u 3 ) 1 3 = 3 ∫ u 2 d u u 3 + u = 3 ∫ u d u u 2 + 1 . \large { I = \int {\frac { { d x}}{ { x + { x ^ {\large\frac{1}{3} \normalsize}}}}} } = {\int {\frac {{ 3{ u ^ 2} d u}} { {{ u ^ 3} + {{ \left( {{ u ^ 3}} \right)} ^ {\large\frac {1} {3} \normalsize}}}}} } \\ \large = { 3\int {\frac{{{u^2}du}} { { {u ^ 3} + u} } } } = { 3 \int {\frac { { u d u}} {{{u ^ 2} + 1 }}} .} I = ∫ x + x 3 1 d x = ∫ u 3 + ( u 3 ) 3 1 3 u 2 d u = 3 ∫ u 3 + u u 2 d u = 3 ∫ u 2 + 1 u d u .
اکنون از تغییر متغیر جدید زیر استفاده میکنیم:
t = u 2 + 1 , d t = 2 u d u , ⇒ u d u = d t 2 . \large { { t = { u ^ 2} + 1,\;\;}\kern-0.3pt{ d t = 2u d u,}\;\;} \Rightarrow { u du = \frac{{ d t} } { 2 } . } t = u 2 + 1 , d t = 2 u d u , ⇒ u d u = 2 d t .
پاسخ نهایی برابر است با:
مثال ۴
انتگرال ∫ d x x 5 – 1 \int {\large\frac{{dx}}{{\sqrt[5]{x} – 1}}\normalsize} ∫ 5 x –1 d x
حل: انتگرال را بهصورت زیر مینویسیم:
∫ d x x 5 – 1 = ∫ d x x 1 5 – 1 . \large { \int { \frac { { d x}} { { \sqrt[\large 5\normalsize] { x } – 1 }} } } = { \int { \frac { {d x }} {{ { x ^ {\large\frac { 1} {5} \normalsize}} – 1}}} .} ∫ 5 x –1 d x = ∫ x 5 1 –1 d x .
از تغییر متغیر زیر استفاده میکنیم:
x 1 5 = u , ⇒ x = u 5 , d x = 5 u 4 d u . \large {{ x ^ {\large\frac { 1 } { 5 }\normalsize}} = u,\;\;}\Rightarrow {{x = { u ^ 5},\;\;}\kern-0.3pt { d x = 5 { u^ 4 }d u . } } x 5 1 = u , ⇒ x = u 5 , d x = 5 u 4 d u .
انتگرال بهصورت زیر درخواهد آمد:
I = ∫ d x x 1 5 – 1 = ∫ 5 u 4 d u u – 1 = 5 ∫ u 4 d u u – 1 . \large {I = \int {\frac{{ d x} }{ { {x ^ {\large\frac{1}{5}\normalsize}} – 1}}} } = {\int {\frac { { 5{ u ^ 4 } du } } { { u – 1}}} } = {5\int {\frac { {{ u ^ 4 }d u } } {{ u – 1 } }} .} I = ∫ x 5 1 –1 d x = ∫ u –1 5 u 4 d u = 5 ∫ u –1 u 4 d u .
از آنجایی که درجه صورت از درجه مخرج بزرگتر است، صورت را بر مخرج تقسیم میکنیم:
u 4 u – 1 = u 3 + u 2 + u + 1 + 1 u – 1 . \large {\frac{{ { u ^ 4} }} { { u – 1}} } = { { { u ^ 3} + { u ^ 2} }+{ u + 1 }+{ \frac{1} {{u – 1}}.}} u –1 u 4 = u 3 + u 2 + u + 1 + u –1 1 .
انتگرال بهصورت زیر محاسبه میشود:
I = 5 ∫ ( u 3 + u 2 + u + 1 + 1 u – 1 ) d u = 5 ( u 4 4 + u 3 3 + u 2 2 + u + ln ∣ u – 1 ∣ ) + C = 5 ( x 4 5 4 + x 3 5 3 + x 2 5 2 + x 5 + ln ∣ x 5 – 1 ∣ ) + C . \large {I }= {{ 5\int {( {{u^3} + {u^2} + u + 1 }}+{{ \frac{1}{{u – 1}}} )du} }} \\ \large ={{ 5 ( {\frac{{{u^4}}}{4} + \frac{{{u^3}}}{3} + \frac{{{u^2}}}{2} }}+{{ u + \ln \left| {u – 1} \right|} ) }+{ C}} \\ \large ={{ 5 ( {\frac{{{\sqrt[\large{5}\normalsize]{x^4}}}}{4} + \frac{{{\sqrt[\large{5}\normalsize]{x^3}}}}{3} + \frac{{{\sqrt[\large{5}\normalsize]{x^2}}}}{2} }}+{{ \sqrt[\large{5}\normalsize]{x} + \ln \left| {\sqrt[\large{5}\normalsize]{x} – 1} \right|} ) }+{ C.}} I = 5 ∫ ( u 3 + u 2 + u + 1 + u –1 1 ) d u = 5 ( 4 u 4 + 3 u 3 + 2 u 2 + u + ln ∣ u –1 ∣ ) + C = 5 ( 4 5 x 4 + 3 5 x 3 + 2 5 x 2 + 5 x + ln 5 x –1 ) + C .
مثال ۵
انتگرال ∫ d x x 3 – x 4 {\large\int\normalsize} {\large\frac{{dx}}{{\sqrt[3]{x} – \sqrt[4]{x}}}\normalsize} ∫ 3 x – 4 x d x
حل: انتگرال را بهصورت زیر مینویسیم:
I = ∫ d x x 3 – x 4 = ∫ d x x 1 3 – x 1 4 . \large {I = \int {\frac { { d x}}{{\sqrt[\large 3\normalsize]{x} – \sqrt[\large 4\normalsize] { x } } }} } = {\int {\frac{{dx}}{{{x^{\large\frac { 1} { 3 }\normalsize}} – { x ^ {\large\frac{1}{4}\normalsize}}}}} .} I = ∫ 3 x – 4 x d x = ∫ x 3 1 – x 4 1 d x .
همانطور که میبینیم، کوچکترین مضرب مشترک مخرج توان جملات x x x n = LCM ( 3 , 4 ) = 12 n= \text{LCM}\left({3,4}\right) = 12 n = LCM ( 3 , 4 ) = 12
u = x 1 12 , ⇒ x = u 12 , d x = 12 u 11 d u . \large {u = { x ^ {\large\frac{1}{ { 12}}\normalsize}},\;\;}\Rightarrow {x = { u ^ { 12} },\;\;}\kern-0.3pt{dx = 12 { u ^ { 11} } d u .} u = x 12 1 , ⇒ x = u 12 , d x = 12 u 11 d u .
در نتیجه، داریم:
I = ∫ 12 u 11 d u ( u 12 ) 1 3 – ( u 12 ) 1 4 = ∫ 12 u 11 d u u 4 – u 3 = 12 ∫ u 8 d u u – 1 . \large{I }={ \int {\frac{{ 1 2{u ^ {11}} d u}}{{{{\left( {{u ^ {12}}} \right)} ^ {\large\frac{1}{3}\normalsize}} – {{\left( {{u ^ { 1 2 }} } \right)} ^ {\large\frac { 1} { 4}\normalsize}}}}} } \\ \large = {\int {\frac{{ 1 2 { u ^ { 11 } }d u } } { { {u ^ 4 } – {u ^3 }} } } } = {1 2\int {\frac {{ { u ^ 8 } d u }} { {u – 1}}} .} I = ∫ ( u 12 ) 3 1 – ( u 12 ) 4 1 12 u 11 d u = ∫ u 4 – u 3 12 u 11 d u = 12 ∫ u –1 u 8 d u .
درجه صورت، از درجه مخرج بزرگتر است. بنابراین، صورت را بر مخرج تقسیم میکنیم:
u 8 u – 1 = u 7 + u 6 + u 5 + u 4 + u 3 + u 2 + u + 1 + 1 u – 1 . \large {\frac{{{u ^ 8 } }} { { u – 1}} } = { { u ^ 7 } + {u ^ 6 } + { u ^ 5 } }+{ {u ^ 4 } + { u^ 3 } + {u ^2 } }+ { u + 1 + \frac{1}{{u – 1}}.} u –1 u 8 = u 7 + u 6 + u 5 + u 4 + u 3 + u 2 + u + 1 + u –1 1 .
بعد از تبدیلات ساده، جواب نهایی بهصورت زیر بهدست میآید:
مثال ۶
انتگرال ∫ d x x – 2 {\large\int\normalsize} {\large\frac{{dx}}{{\sqrt {\sqrt x – 2} }}\normalsize} ∫ x –2 d x
حل: از تغییر متغیر زیر استفاده میکنیم:
x – 2 = u 2 , ⇒ x = u 2 + 2 , ⇒ x = ( u 2 + 2 ) 2 = u 4 + 4 u 2 + 4 , ⇒ d x = ( 4 u 3 + 8 u ) d u . \large {\sqrt x – 2 = {u^2},\;\;}\Rightarrow {\sqrt x = {u ^ 2 } + 2,\;\;} \\ \large\Rightarrow {x = {\left( {{ u ^ 2} + 2} \right) ^ 2} }={ { u ^ 4} + 4{ u ^2 } + 4,\;\;}\Rightarrow {dx = \left( { 4{ u ^ 3} + 8u} \right)du.} x –2 = u 2 , ⇒ x = u 2 + 2 , ⇒ x = ( u 2 + 2 ) 2 = u 4 + 4 u 2 + 4 , ⇒ d x = ( 4 u 3 + 8 u ) d u .
در نتیجه، داریم:
I = ∫ d x x – 2 = ∫ ( 4 u 3 + 8 u ) d u u = 4 ∫ ( u 2 + 2 ) d u = 4 u 3 3 + 8 u + C = 4 3 ( x – 2 ) 3 + 8 x – 2 + C . \large {I = \int {\frac { { d x}}{{\sqrt {\sqrt x – 2} }}} } = {\int { \frac { {\left( { 4 {u ^ 3 } + 8 u } \right)d u} } { u }} } = {4\int {\left( {{ u ^2 } + 2} \right) du } } \\ \large = {\frac{{4 { u^ 3}}}{3} + 8u + C } = {{\frac{4} { 3}\sqrt {{{\left( {\sqrt x – 2} \right)} ^ 3 }} }+{ 8\sqrt {\sqrt x – 2} + C.}} I = ∫ x –2 d x = ∫ u ( 4 u 3 + 8 u ) d u = 4 ∫ ( u 2 + 2 ) d u = 3 4 u 3 + 8 u + C = 3 4 ( x –2 ) 3 + 8 x –2 + C .
مثال ۷
انتگرال ∫ e x + 1 d x {\large\int\normalsize} {\sqrt {{e^x} + 1}\,dx} ∫ e x + 1 d x
حل: از تغییر متغیر زیر استفاده میکنیم:
e x + 1 = u 2 , ⇒ e x d x = 2 u d u , ⇒ d x = 2 u d u e x = 2 u d u u 2 – 1 . \large {{e ^ x } + 1 = { u ^ 2 },\;\;}\Rightarrow { { e ^ x} d x = 2 u d u,\;\;} \\ \large \Rightarrow { {d x = \frac{ { 2 u du } }{ { { e ^ x }} } }= { \frac{{ 2 u d u } }{ { { u ^ 2} – 1}}.}} e x + 1 = u 2 , ⇒ e x d x = 2 u d u , ⇒ d x = e x 2 u d u = u 2 –1 2 u d u .
و حاصل انتگرال بهصورت زیر بهدست میآید:
I = ∫ e x + 1 d x = ∫ u 2 u d u u 2 – 1 = 2 ∫ u 2 d u u 2 – 1 = 2 ∫ u 2 – 1 + 1 u 2 – 1 d u = 2 ∫ ( 1 + 1 u 2 – 1 ) d u = 2 ∫ d u − 2 ∫ d u 1 – u 2 = 2 u − 2 ⋅ 1 2 ln ∣ 1 + u 1 – u ∣ + C = 2 u – ln ∣ 1 + u 1 – u ∣ + C = 2 e x + 1 − ln ∣ 1 + e x + 1 1 – e x + 1 ∣ + C . \large {I = \int {\sqrt {{ e ^ x } + 1} d x } } = {\int { u \frac { {2 u d u } } { { { u ^ 2 } – 1}}} } = { 2 \int {\frac {{ { u ^ 2 } d u }}{{{u ^ 2} – 1}}} } \\ \large = {2\int {\frac{{ { u ^ 2 } – 1 + 1 } } { { { u ^ 2} – 1 } }d u} } = {2\int {\left( {1 + \frac { 1} { { { u ^ 2} – 1 } }} \right)du} } \\ \large = { { 2 \int { d u } } - { 2\int {\frac { {d u } }{ { 1 – { u ^ 2 } } } } }} = { { 2 u } - { 2 \cdot \frac{1}{2}\ln \left| {\frac{{1 + u}}{{1 – u}}} \right| }+{ C }} \\ \large = {{2u – \ln \left| {\frac{{1 + u}}{{1 – u}}} \right| }+{ C }} = {{2\sqrt {{e^x} + 1} }-{ \ln \left| {\frac{{1 + \sqrt {{e^x} + 1} }}{{1 – \sqrt {{e^x} + 1} }}} \right| }+{ C.}} I = ∫ e x + 1 d x = ∫ u u 2 –1 2 u d u = 2 ∫ u 2 –1 u 2 d u = 2 ∫ u 2 –1 u 2 –1 + 1 d u = 2 ∫ ( 1 + u 2 –1 1 ) d u = 2 ∫ d u − 2 ∫ 1– u 2 d u = 2 u − 2 ⋅ 2 1 ln 1– u 1 + u + C = 2 u – ln 1– u 1 + u + C = 2 e x + 1 − ln 1– e x + 1 1 + e x + 1 + C .
فیلم های آموزش انتگرال توابع گنگ – از صفر تا صد (+ دانلود فیلم آموزش گام به گام) فیلم آموزشی انتگرال توابع گنگ فیلم آموزشی حل چند مثال از انتگرال توابع گنگ 
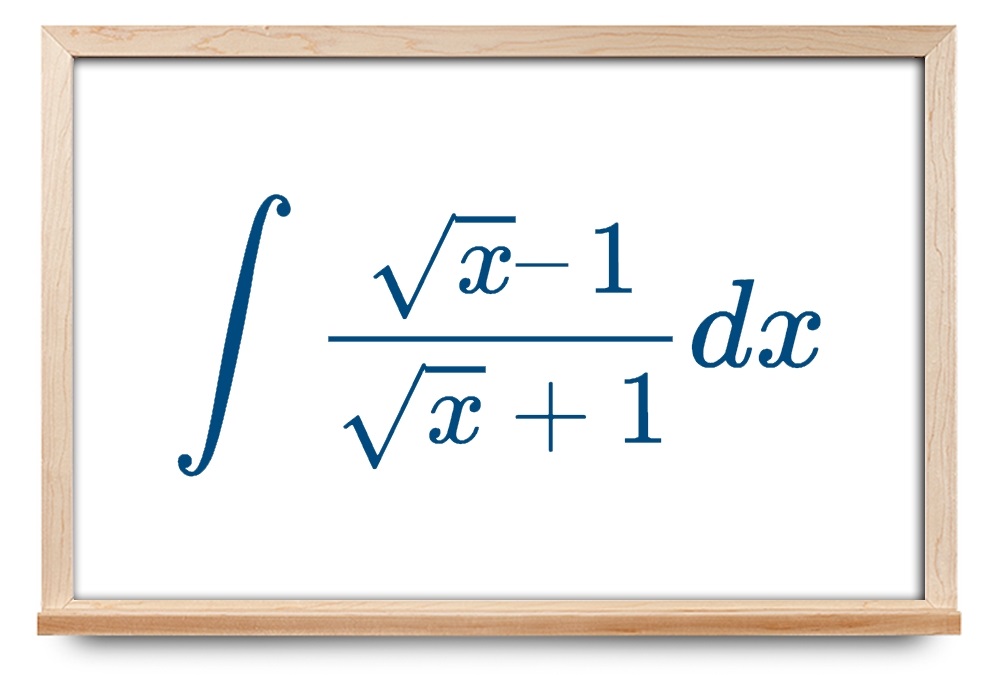
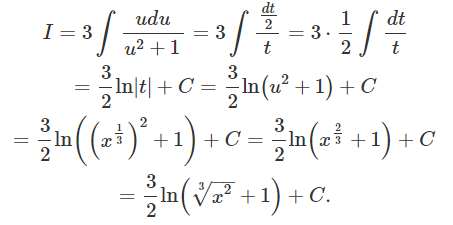
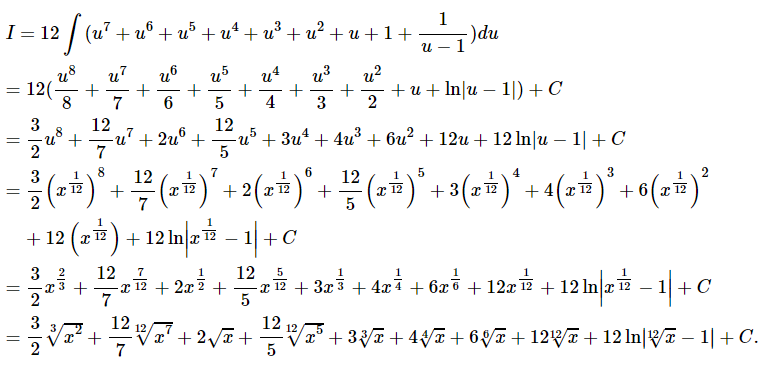













خیلی ممنوننننننننننننن