مرکز برش و کاربرد آن در تحلیل تیرها – به زبان ساده

در مباحث «تحلیل تیرهای کامپوزیتی»، «روش مقطع معادل برای تحلیل تیرهای کامپوزیتی»، «تحلیل تیرهای دارای تقارن مضاعف تحت بارهای مورب» و «تحلیل خمش در تیرهای نامتقارن»، تنش‌های خمشی اعمال شده بر روی تیرها را در شرایط مختلف بررسی کردیم. با وجود اینکه بارگذاری‌های جانبی نیز همانند گشتاورهای خمشی باعث ایجاد نیروهای برشی می‌شوند، در هیچ یک از مباحث مذکور، تأثیر این بارگذاری‌های را مورد ارزیابی قرار ندادیم. در مباحث «تحلیل تنش‌های برشی در تیرهای مستطیلی»، «تحلیل تنش‌های برشی در تیرهای دایره‌ای» و «تحلیل تنش‌های برشی در جانِ تیر» نیز با نحوه تعیین تنش‌های برشی در هنگام اعمال بار بر روی صفحه تقارن آشنا شدیم. در این مباحث، رابطه برش برای محاسبه تنش‌های برشی در تیرهایی با شکل‌های متفاوت را به دست آوردیم.

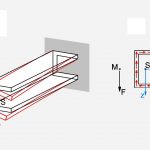
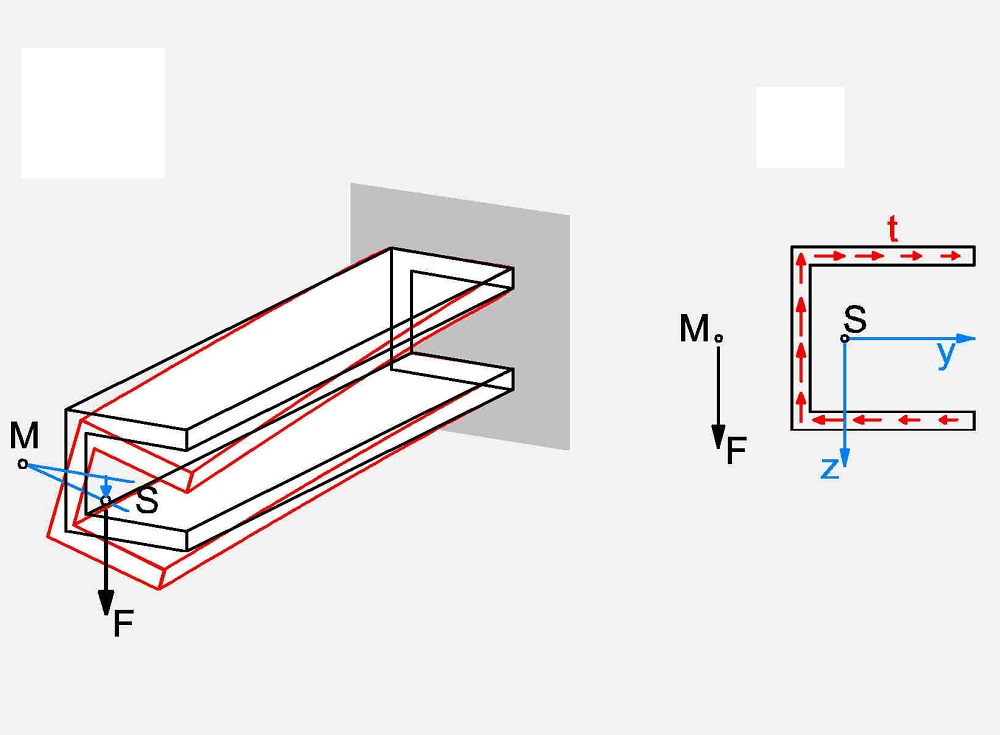
در این مقاله شرایطی را بررسی خواهیم کرد که در آن، بارهای جانبی بر روی صفحه تقارن اعمال نمی‌شوند. در این شرایط، مشاهده خواهید کرد که با فرض عدم وجود پیچش، بارهای اعمال شده از روی نقطه خاصی به نام «مرکز برش» (Shear Center) عبور می‌کنند. مرکز برش، یکی از مهم‌ترین مفاهیم مورد نیاز برای تحلیل تنش‌های برشی موجود در تیرها است.

مرکز برش در سطح مقطع متقارن

تیر یکسر گیردار زیر که انتهای آزاد آن تحت بار P قرار دارد را در نظر بگیرید. این تیر تنها دارای یک محور تقارن است. به تیرهایی که سطح مقطع آن‌ها مشابه شکل زیر باشد، «تیر I نامتوازن» (Unbalanced I-Beam) گفته می‌شود. تیرهای I شکل (متوازن یا نامتوازن) معمولاً در صفحه تقارن خود (صفحه xz) تحت بار قرار می‌گیرند اما در مثال زیر، خط اثر نیروی P بر صفحه مذکور عمود است.

فیلم آموزش مقاومت مصالح 1 و 2 – مرور و حل مساله در فرادرس

کلیک کنید

به دلیل قرارگیری مبدأ مختصات بر روی مرکز هندسی سطح مقطع و همچنین در نظر گرفتن محور z به عنوان محور تقارن، محورهای y و z به عنوان محورهای اصلی گذرنده از مرکز هندسی (محورهای اصلی مرکزی) محسوب می‌شوند.

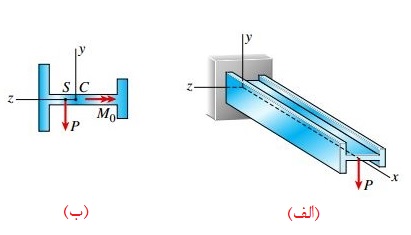
فرض کنید که تیر بالا در اثر اعمال بار P خم شود. در صورت خنثی بودن صفحه xz، خمش بر روی آن رخ می‌دهد. به این ترتیب، دو برآیند تنش در مقطع میانی تیر به وجود می‌آید. اولین برآیند، گشتاور خمشی M₀ است که حول محور z و در جهت منفی این محور اعمال می‌شود. دومین برآیند، نیروی برشی P است که در جهت منفی محور y عمل می‌کند. در یک تیر که تحت بارگذاری مشخص قرار دارد، کمیت‌های M₀ و P معلوم هستند.

برآیند تنش‌های نرمال اعمال شده بر روی سطح مقطع برابر گشتاور خمشی M₀ و برآیند تنش‌های برشی برابر نیروی برشی P است. اگر رفتار ماده سازنده تیر از قانون هوک پیروی کند، رابطه بین تغییرات تنش‌های نرمال با فاصله نقطه مورد نظر تا محور خنثی (محور z) به صورت خطی خواهد بود. در این حالت می‌توان مقدار تنش‌های نرمال را با استفاده از رابطه خمش تعیین کرد.

از آنجایی که محاسبه تنش‌های برشی اعمال شده بر سطح مقطع بر اساس فرضیات تعادل و با استفاده از مقادیر تنش‌های نرمال صورت می‌گیرد، توزیع این تنش‌ها بر روی سطح مقطع نیز به همین صورت قابل تعیین خواهد بود. برآیند تنش‌های برشی به صورت یک نیروی عمودی است. مقدار این نیرو با مقدار نیروی P برابر بوده و خط اثر آن از نقطه‌ای بر روی محور z عبور می‌کند (نقطه S در شکل زیر). این نقطه با عنوان مرکز برش یا «مرکز خمش» (Center of Flexure) شناخته می‌شود.

به طور خلاصه، با در نظر گرفتن محور z به عنوان محور خنثی، علاوه بر توزیع تنش‌های نرمال، امکان تعیین توزیع تنش‌های برشی و موقعیت قرارگیری برآیند نیروی برشی نیز فراهم می‌شود. به این ترتیب، برای رخ دادن خمش در این حالت، بار اعمال شده P بر انتهای آزاد تیر باید از یک نقطه بخصوص (مرکز برش) عبور کند. اگر بار در نقطه دیگری بر روی محور z (مثلاً نقطه A) اعمال شده باشد، می‌توان آن را با یک مجموعه استاتیکی معادل شامل یک نیروی گذرنده از مرکز برش (P) و یک گشتاور (T) جایگزین کرد (شکل زیر). در این شرایط، نیروی P باعث ایجاد خمش حول محور z و گشتاور T باعث ایجاد پیچش می‌شود. در نتیجه، اگر یک بار جانبی بر روی یک تیر اعمال شود و از مرکز برش آن عبور کند، خمش بدون پیچش رخ می‌دهد.

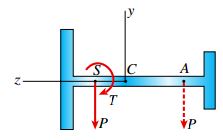
مرکز برش نیز مانند مرکز هندسی، بر روی محور تقارن قرار دارد. به همین دلیل در یک سطح مقطع با تقارن مضاعف (شکل زیر)، مرکز برش S و مرکز هندسی C بر روی یکدیگر قرار می‌گیرند. در این حالت، بار P گذرنده از مرکز هندسی باعث ایجاد خمش بدون پیچش حول محورهای y و z می‌شود. نحوه تعیین تنش‌های خمشی ناشی از اعمال این بار در مبحث «تحلیل تیرهای دارای تقارن مضاعف» توضیح داده شده است.

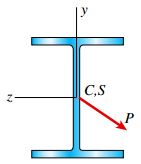
اگر یک تیر دارای سطح مقطعی با تقارن منفرد باشد، مرکز هندسی و مرکز برش آن بر روی محور تقارن قرار خواهند داشت. در این حالت می‌توان بار گذرنده از مرکز برش را به دو مؤلفه در راستای محورهای y و z تجزیه کرد. با در نظر گرفتن محور z به عنوان محور خنثی، مؤلفه هم‌راستا با محور y باعث ایجاد خمش در صفحه xy می‌شود. با در نظر گرفتن محور y به عنوان محور خنثی، مؤلفه هم‌راستا با محور z باعث ایجاد خمش بدون پیچش در صفحه xz می‌شود. مقدار تنش‌های خمشی حاصل از این مؤلفه‌ها، با کمک برهم‌نهی تنش‌های حاصل از بار اصلی به دست می‌آید.

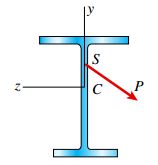
مرکز برش در سطح مقطع نامتقارن

در صورتی که یک تیر دارای سطح مقطع نامتقارن باشد و بار اعمال شده بر آن از مرکز برش گذر کند، فرآیند تحلیل خمش تیر دارای سه مرحله کلی خواهد بود. در مرحله اول، محل قرارگیری مرکز هندسی سطح مقطع (نقطه C) و نحوه جهت‌گیری محورهای اصلی گذرنده از آن (محورهای اصلی مرکزی y و z) را تعیین می‌کنیم.

فیلم آموزش مقاومت مصالح – ویژه رشته عمران در فرادرس

کلیک کنید

سپس، با تجزیه بار به مؤلفه‌های هم‌راستا با محورهای y و z، گشتاورهای خمشی M_y و M_z حول محورهای اصلی را به دست می‌آوریم. در مرحله آخر، با استفاده از روش ارائه شده در مبحث «تحلیل خمش در تیرهای نامتقارن»، مقدار تنش‌های خمشی را مورد محاسبه قرار می‌دهیم.

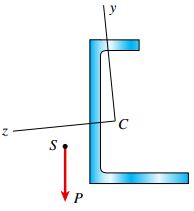
در این مقاله با اهمیت مرکز برش در تحلیل تیرها آشنا شدیم. مسئله مهم دیگر در مبحث مرکز برش، نحوه تعیین محل قرارگیری آن است. برای تیرهای دارای تقارن مضاعف، مرکز برش بر روی مرکز هندسی سطح مقطع قرار دارد. در تیرهای دارای تقارن منفرد، این مرکز بر روی محور تقارن قرار می‌گیرد اما تعیین محل دقیق آن نیاز به تحلیل دارد. اگر سطح مقطع تیر نامتقارن باشد، پیچیدگی مراحل تعیین محل قرارگیری مرکز برش افزایش می‌یابد. در این مورد، باید از روش‌های پیشرفته‌تری استفاده کرد.

در مبحث تعیین محل قرارگیری مرکز برش، تیرهای جدار نازک با سطح مقطع باز نظیر تیرهای بال پهن، ناودانی‌ها، نبشی‌ها، تیرهای T و مقاطع Z، حالت‌های خاص به شمار می‌روند. این تیرها کاربرد بسیار زیادی در ساخت سازه‌های مختلف و همچنین مقاومت بسیار کمی در برابر پیچش دارند. به همین دلیل، تعیین موقعیت مرکز برش در آن‌ها از اهمیت ویژه‌ای برخوردار است. در مباحث بعدی، به ارائه نحوه تعیین مرکز برش در تیرهای مذکور خواهیم پرداخت.

^^