قانون هوک برای حالت تنش صفحه ای – روابط و حالت های خاص

در مباحث «تنش صفحه‌ای»، «تنش‌های اصلی و تنش‌های برشی ماکسیمم» و «رسم دایره مور برای حالت تنش صفحه ای»، با نحوه تحلیل تنش‌های اعمال شده بر روی صفحات دوران‌یافته آشنا شدیم. در مبحث «نسبت پواسون و رفتار مواد در محدوده الاستیک» نیز به معرفی قانون هوک در مواد الاستیک خطی پرداختیم و اشاره کردیم که حالت تنش برای اکثر سازه‌ها و دستگاه‌ها پیچیده بوده و تحلیل آن‌ها نیازمند استفاده از معادلات تعمیم‌یافته قانون هوک است. در این مقاله، به معرفی فرم تعمیم‌یافته قانون هوک و حالت‌های خاص آن برای حالت تنش صفحه‌ای خواهیم پرداخت. علاوه بر این، روابط مرتبط با چگالی انرژی کرنشی برای این حالت و همچنین برای حالت‌های خاص مربوط به آن را نیز ارائه خواهیم کرد.

رابطه کلی قانون هوک برای تنش صفحه‌ای

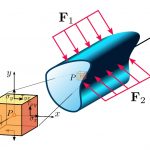
شکل زیر، تنش‌های اعمال شده بر روی صفحات دوران‌یافته یک المان در حالت تنش صفحه‌ای را نمایش می‌دهد. به منظور دستیابی به معادلات تبدیل ارائه شده برای این حالت نیازی به استفاده از خواص ماده نیست؛ چراکه این معادلات تنها بر اساس تعادل المان به دست می‌آیند.

در این مقاله، به منظور بررسی تأثیر کرنش‌های به وجود آمده درون یک ماده، دو شرط بسیار مهم زیر را در نظر می‌گیریم:

• همگن و همسانگرد بودن: ماده تشکیل‌دهنده جسم، یکنواخت و خواص آن در همه جهات، یکسان است.
• رفتار الاستیک خطی: ماده از قانون هوک پیروی می‌کند.

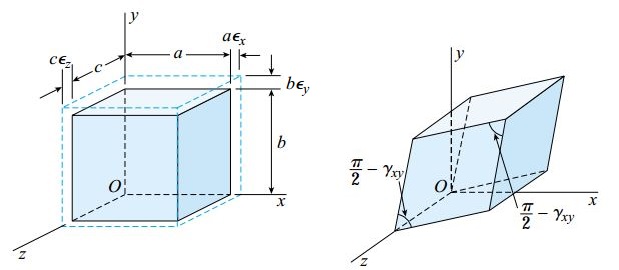
در صورت برقرار بودن شرایط بالا می‌توان رابطه بین تنش‌ها و کرنش‌های درون یک جسم را به راحتی تعیین کرد. مطابق شکل زیر، کرنش‌های نرمال ε_y ،ε_x و ε_z را برای حالت تنش صفحه‌ای در نظر بگیرید. این شکل، تأثیر کرنش‌های مذکور بر روی تغییر شکل المانی با ابعاد b ،a و c را نمایش می‌دهد. تمام کرنش‌های نمایش داده شده در این شکل مثبت هستند. با جایگذاری تأثیر هر یک از تنش‌های نمایش داده شده در شکل بالا می‌توان مقادیر کرنش را بر حسب مؤلفه‌های تنش بیان کرد.

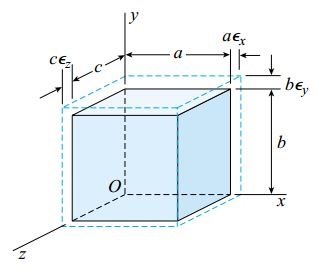
به عنوان مثال، کرنش نرمال ε_x در راستای محور x را در نظر بگیرید. میزان کرنش ایجاد شده بر اثر اعمال تنش نرمال σ_x، از رابطه σ_x/E به دست می‌آید. پارامتر E، مقدار مدول الاستیسیته ماده را نمایش می‌دهد. میزان کرنش ایجاد شده بر اثر اعمال تنش نرمال σ_y نیز از طریق رابطه νσ_y/E- قابل محاسبه است. پارامتر ν، نسب پواسون ماده را نمایش می‌دهد. اعمال تنش برشی τ_xy باعث ایجاد کرنش نرمال در جهات y ،x و z نمی‌شود. بنابراین، برآیند کرنش به وجود آمده در جهت x برابر است با:

به همین ترتیب، کرنش‌های به وجود آمده در جهات y و z نیز قابل محاسبه خواهند بود:

در صورت مشخص بودن مقادیر تنش می‌توان با استفاده از معادلات بالا مقادیر کرنش در حالت تنش صفحه‌ای را تعیین کرد. تنش برشی τ_xy باعث ایجاد انحراف در المان و تبدیل آن به یک متوازی‌الاضلاع لوزی شکل می‌شود (شکل زیر). میزان کاهش زاویه بین صفحات x و y، کرنش برشی γ_xy حاصل از اعمال این تنش برشی را نمایش می‌دهد.

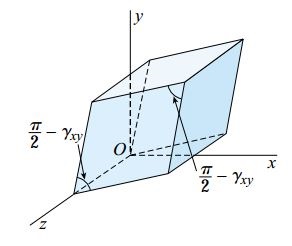
با توجه قانون هوک برای مواد تحت برش، رابطه بین تنش و کرنش به صورت زیر تعریف می‌شود:

G: مدول برشی الاستیسیته

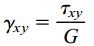
توجه داشته باشید که تنش‌های نرمال σ_x و σ_y هیچ تأثیری بر روی میزان کرنش برشی γ_xy ندارند. در نتیجه با استفاده از روابط بالا در حالت تنش صفحه‌ای می‌توان مقادیر کرنش‌های نرمال و برشی را در هنگام اعمال هم‌زمان تمام تنش‌ها محاسبه کرد. با ترکیب روابط کرنش‌های نرمال (ε_y ،ε_x و ε_z) و بازنویسی آن‌ها بر اساس پارامترهای تنش (σ_y ،σ_x و σ_z)، روابط زیر به دست می‌آیند:

علاوه بر این، رابطه تعیین تنش برشی نیز به صورت زیر نوشته می‌شود:

در صورت مشخص بودن مقادیر کرنش در یک مسئله می‌توان از روابط بالا برای یافتن مقادیر تنش استفاده کرد. تمامی روابط معرفی شده از ابتدای مقاله تا به اینجا با عنوان «قانون هوک برای تنش صفحه‌ای» شناخته می‌شوند. این روابط دارای سه ثابت مرتبط با خواص ماده (G ،E و ν) هستند. با این وجود، تنها دو پارامتر E و ν به عنوان ثابت‌های مستقل به شمار می‌روند؛ چراکه پارامتر G از طریق رابطه زیر به دو پارامتر دیگر وابسته است:

حالت‌های خاص قانون هوک برای تنش صفحه‌ای

در حالت «تنش دومحوری» (Biaxial Stress)، تنش برشی τ_xy برابر با صفر است. از این‌رو، قانون هوک برای تنش صفحه‌ای به شکل زیر درمی‌آید:

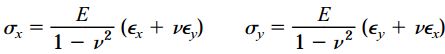
روابط بالا هیچ تفاوتی با روابط قبلی ندارند؛ چراکه تأثیر تنش‌های نرمال و برشی مستقل از یکدیگر است.

فیلم آموزش مقاومت مصالح 1 و 2 – مرور و حل مساله در فرادرس

کلیک کنید

در حالت «تنش تک‌محوری» (Uniaxial Stress)، تنش نرمال σ_y برابر با صفر خواهد بود. بنابراین، قانون هوک برای تنش صفحه‌ای ساده‌تر از حالت قبل می‌شود:

در حالت «برش خالص» (Pure Shear)، تنش‌های نرمال σ_y و σ_z برابر با صفر هستند. به این ترتیب، قانون هوک برای تنش صفحه‌ای به شکل زیر درمی‌آید:

در تمام این سه حالت خاص، مقدار تنش نرمال σ_z برابر با صفر است.

تغییرات حجم

هنگامی که یک جسم جامد در معرض کرنش قرار می‌گیرد، علاوه بر ابعاد، حجم آن نیز تغییر می‌کند. در صورت مشخص بودن مقادیر کرنش‌های نرمال در سه جهت عمود بر هم، میزان تغییر حجم جسم قابل محاسبه خواهد بود. برای نشان دادن نحوه انجام این محاسبات، المان کوچک نمایش داده شده در شکل زیر را در نظر بگیرید.

پیش از رخ دادن کرنش‌ها، طول ابعاد المان بالا در راستای y ،x و z، به ترتیب برابر b، a و c است. با ایجاد کرنش‌های ε_y ،ε_x و ε_z، ابعاد المان مطابق با خط‌چین نمایش داده شده در شکل بالا تغییر می‌کنند. به این ترتیب، میزان افزایش طول هر بعد برابر با bε_y ، aε_x و cε_z خواهد بود. حجم اولیه المان (V₀) از طریق رابطه زیر محاسبه می‌شود:

و حجم نهایی آن (V₁) نیز به کمک رابطه زیر تعیین می‌شود:

با قرار دادن V₀ به جای عبارت abc در رابطه، به رابطه زیر می‌رسیم:

اگر عبارت سمت راست رابطه بالا را بسط دهیم، رابطه زیر به دست می‌آید:

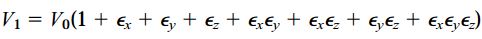
این روابط برای محاسبه کرنش‌های کوچک و کرنش‌های بزرگ قابل استفاده هستند. اگر میزان کرنش‌های به وجود آمده بسیار کوچک باشد، حاصل‌ضرب هر دو کرنش (مانند ε_xε_y) در مقایسه با مقدار هر یک از کرنش‌ها (مانند ε_x یا ε_y) کوچک خواهد بود. در این شرایط می‌توان از عبارت‌های شامل ضرب دو کرنش صرف نظر کرد. بنابراین، رابطه مربوط به محاسبه حجم نهایی المان به شکل زیر تغییر می‌کند:

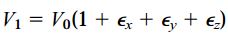
به این ترتیب، اختلاف حجم المان برابر است با:

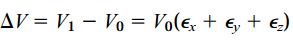
رابطه بالا برای اجسامی با کرنش‌های کوچک و یکنواخت کاربرد دارد. توجه داشته باشید که در این رابطه، پیروی ماده از قانون هوک ضروری نیست. علاوه بر این، رابطه بالا نه‌تنها برای حالت تنش صفحه‌ای، بلکه برای تمام حالت‌های تنش قابل استفاده است. به عنوان یک نکته تکمیلی باید اشاره کنیم که در اثر اعمال کرنش‌های برشی هیچ تغییری در حجم جسم رخ نمی‌دهد. تغییر حجم واحد (e) یا «اتساع» (Dilatation)، به صورت تغییرات حجم تقسیم بر حجم اولیه تعریف می‌شود. بنابراین:

با به کارگیری این رابطه برای المان‌های حجم و انتگرال‌گیری از آن می‌توان تغییرات حجم یک جسم را حتی در صورت غیر یکنواخت بودن کرنش‌های نرمال محاسبه کرد. معادلات ارائه شده هم برای کرنش‌های فشاری و هم برای کرنش‌های کششی قابل استفاده هستند. بر اساس قواعد علامت‌گذاری، افزایش حجم با علامت مثبت و کاهش حجم با علامت منفی نمایش داده می‌شود. این قاعده برای هر دو کمیت e و ΔV صادق است.

فیلم آموزش مقاومت مصالح ۲ + مفاهیم کلیدی در فرادرس

کلیک کنید

اکنون موادی را در نظر بگیرید که از قانون هوک پیروی می‌کنند و تنها در معرض تنش صفحه‌ای قرار دارند. در این شرایط، کرنش‌های ε_y ،ε_x و ε_z با استفاده از معادلات ارائه شده در بخش‌های قبلی تعیین می‌شوند. با جایگذاری این معادلات در رابطه e خواهیم داشت:

توجه داشته باشید که رابطه بالا برای حالت تنش دومحوری نیز قابل استفاده است. در حالت تنش تک‌محوری، رابطه بالا به صورت زیر ساده می‌شود:

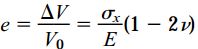
با توجه به این رابطه مشاهده می‌شود که بیشترین مقدار ممکن برای نسبت پواسون در مواد معمولی 0.5 است. اگر این مقدار بیشتر از 0.5 باشد، حجم در شرایط بارگذاری کششی کاهش می‌یابد. این مسئله خلاف رفتار فیزیکی مواد در حالت عادی است.

چگالی انرژی کرنشی در تنش صفحه‌ای

چگالی انرژی کرنشی (u)، میزان انرژی کرنشی ذخیره‌شده در واحد حجم ماده را نمایش می‌دهد. به منظور آشنایی با نحوه تعیین این کمیت برای یک المان تحت تنش صفحه‌ای، شکل‌های زیر را در نظر بگیرید. به دلیل مستقل بودن کرنش‌های نرمال و برشی از هم، انرژی کرنشی کل از جمع انرژی هر یک از این موارد به دست می‌آید.

در مرحله اول، انرژی کرنشی ناشی از کرنش‌های نرمال را تعیین می‌کنیم. σ_x، تنش اعمال شده بر روی صفحه x را نمایش می‌دهد. به این ترتیب، میزان نیروهای اعمال شده بر این صفحه از رابطه σ_xbc به دست می‌آید. با شروع بارگذاری، نیروهای اعمال شده از مقدار صفر به یک مقدار حداکثری می‌رسند. هم‌زمان با رخ دادن این فرآیند، صفحه x المان به اندازه aε_x جابجا می‌شود. کار انجام شده با حاصل‌ضرب نیرو در جابجایی برابر است. بنابراین:

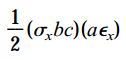
کاربرد این رابطه برای موادی است که از قانون هوک پیروی می‌کنند. به همین ترتیب، اعمال نیروی σ_yac بر روی صفحه y باعث انجام کاری معادل با عبارت زیر می‌شود:

با جمع دو عبارت قبلی، رابطه انرژی کرنشی ذخیره‌شده در المان مورد بررسی به دست می‌آید:

به این ترتیب، چگالی انرژی کرنشی ناشی از اعمال تنش‌ها و کرنش‌های نرمال برابر است با:

چگالی انرژی کرنشی ناشی از اعمال تنش‌ها و کرنش‌های برشی نیز عبارت است از:

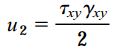
با جمع دو رابطه بالا، به رابطه چگالی انرژی کرنشی برای حالت تنش صفحه‌ای دست می‌یابیم:

با استفاده از معادلات قانون هوک می‌توان چگالی انرژی کرنشی را بر اساس مؤلفه‌های تنش بیان کرد:

به همین ترتیب، با استفاده از معادلات قانون هوک، رابطه چگالی انرژی کرنشی بر اساس مؤلفه‌های کرنش نیز قابل تعریف خواهد بود:

با حذف عبارات مربوط به برش (τ_xy یا γ_xy) در روابط بالا، معادله چگالی انرژی کرنشی برای حالت تنش دومحوری به دست می‌آید. علاوه بر این، با در نظر گرفتن مقادیر زیر، معادله چگالی انرژی کرنشی برای حالت تنش تک‌محوری نیز تعیین می‌شود:

برای تعیین چگالی انرژی کرنش در حالت برش خالص، مقادیر زیر را در روابط اصلی جایگزین می‌کنیم:

^^