تحلیل تنش های برشی در تیرهای بال پهن – با مثال های کاربردی

در مباحث «تحلیل تنش برشی در تیرهای مستطیلی» و «تحلیل تنش برشی در تیرهای دایره‌ای»، به بررسی وضعیت تنش‌های موجود در تیرهایی با سطح مقطع مستطیلی و دایره‌ای پرداختیم. در این مقاله قصد داریم تنش‌های برشی موجود در تیرهای بال پهن را مورد تحلیل قرار دهیم. در انتها نیز به منظور آشنایی بهتر با نحوه به کارگیری روابط ارائه شده، به تشریح چند مثال کاربردی خواهیم پرداخت.

تیر بال پهن

اگر یک تیر H یا اصطلاحاً «بال پهن» (Wide-Flange) مانند شکل زیر در معرض نیروهای برشی و گشتاورهای خمشی (خمش غیر یکنواخت) قرار گیرد، تنش‌های نرمال و برشی بر روی مقاطع عرضی تیر به وجود می‌آیند.

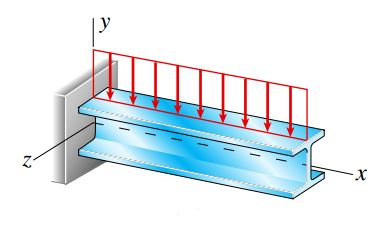
توزیع تنش‌های برشی در یک تیر بال پهن پیچیده‌تر از توزیع این تنش‌ها در یک تیر مستطیلی است.

فیلم آموزش مقاومت مصالح – مرور و حل تست کنکور ارشد در فرادرس

کلیک کنید

به عنوان مثال، تنش‌های برشی موجود در بال‌های این تیر مانند شکل زیر در هر دو جهت عمودی و افقی (محور y و z) اعمال می‌شود. معمولاً تنش‌های برشی افقی در بال‌های تیر بسیار بزرگ‌تر از تنش‌های برشی عمودی هستند.

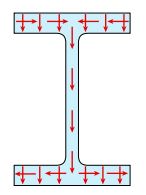
تنش‌های برشی موجود در جانِ یک تیر بال پهن تنها در راستای عمودی اعمال می‌شوند و بزرگ‌تر از تنش‌های موجود در بال‌ها هستند. مقدار این تنش‌ها با استفاده از روش‌های معرفی شده در مبحث «تحلیل تنش‌های برشی در تیرهای مستطیلی» قابل محاسبه است.

تنش‌های برشی در جانِ تیر

به منظور تحلیل جانِ تیر، شکل زیر را در نظر بگیرید. مرحله اول تحلیل را با تعیین تنش‌های برشی موجود در خط ef شروع می‌کنیم. به این منظور، همانند تحلیل تنش‌های برشی در تیرهای مستطیلی فرض می‌کنیم که این تنش‌ها در جانِ تیر بال پهن نیز موازی با محور y هستند و به طور یکنواخت در عرض (ضخامت) جان توزیع شده‌اند.

فیلم آموزش مقاومت مصالح 1 و 2 – مرور و حل مساله در فرادرس

کلیک کنید

به این ترتیب می‌توان به راحتی از رابطه برش (τ=VQ/Ib) برای محاسبه تنش‌های برشی استفاده کرد. اگرچه، اکنون به جای عرض تیر b، ضخامتِ جان t مورد استفاده قرار می‌گیرد. به علاوه، مساحت مورد استفاده برای محاسبه گشتاور اول Q، مساحت بین خط ef و لبه بالایی سطح مقطع تیر (ناحیه پررنگ) است.

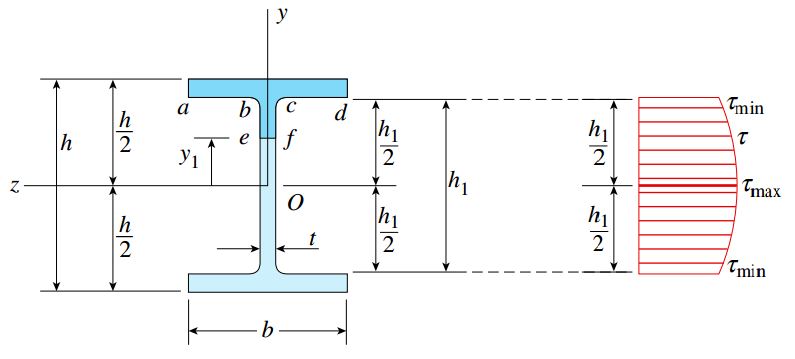
هنگام تعیین گشتاور اول Q برای سطح پررنگ، از تأثیر ماهیچه (Fillet) در محل اتصال جان به بال (نقاط b و c) صرف‌نظر می‌شود. خطای حاصل از نادیده گرفتن این نواحی بسیار کوچک است. برای انجام محاسبات گشتاور اول، سطح پررنگ را به دو مستطیل مجزا تقسیم می‌کنیم. بالِ بالایی تیر به عنوان مستطیل اول در نظر گرفته می‌شود:

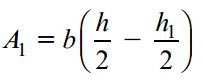
b: عرض بال؛ h: ارتفاع کل تیر؛ h₁: فاصله داخلی بین بال‌ها

ناحیه بین خط ef و بال تیر (مستطیل efcb) را نیز به عنوان مستطیل دوم در نظر می‌گیریم:

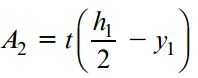
t: ضخامت جان؛ y₁: فاصله از محور خنثی تا خط ef

گشتاور اول نواحی A₁ و A₂ حول محور خنثی با حاصل‌ضرب مساحت این نواحی در فاصله مرکز هندسی‌شان تا محور z برابر است. با جمع گشتاورهای اول این دو ناحیه، گشتاور اول Q ناحیه پررنگ به دست می‌آید:

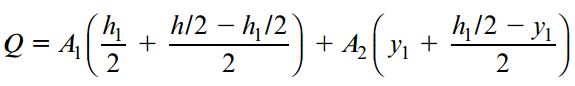
با جایگذاری عبارت‌های A₁ و A₂ در رابطه بالا و ساده‌سازی آن به رابطه زیر می‌رسیم:

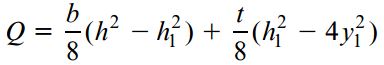
به این ترتیب، تنش برشی τ جانِ تیر در فاصله y₁ نسبت به محور خنثی برابر است با:

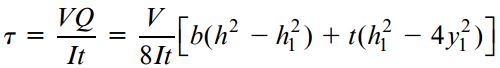
ممان اینرسی موجود در رابطه بالا به صورت زیر تعیین می‌شود:

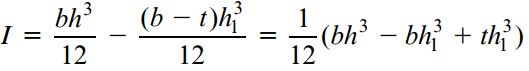
تمام کمیت‌های رابطه τ به جز y₁ کمیت‌های ثابت هستند. به همین دلیل، تنش برشی بر روی ارتفاع جانِ تیر به صورت درجه دو (سهمی‌وار) تغییر می‌کند (شکل زیر). نمودار نمایش داده شده در شکل زیر تنها برای جان تیر رسم شده و بخش بال‌های تیر را در برنمی‌گیرد. توجه داشته باشید که رابطه معرفی شده در این بخش برای بال‌های تیر قابل استفاده نیست (دلیل این موضوع در بخش‌های بعدی توضیح داده خواهد شد).

تنش‌های برشی ماکسیمم و مینیمم

تنش برشی ماکسیمم در یک تیر بال پهن بر روی محور خنثی (y₁=0) و تنش برشی مینیمم در محل برخورد جان با بال‌ها (y₁=±h₁/2) رخ می‌دهد. به این ترتیب داریم:

فیلم آموزش مقاومت مصالح – ویژه رشته عمران در فرادرس

کلیک کنید

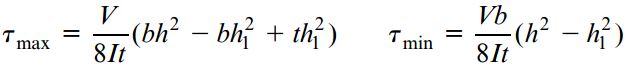
برای تیرهای بال پهن معمولی، تنش ماکسیمم حدود 10 تا 60 درصد از تنش مینیمم بزرگ‌تر است. توجه داشته باشید که این تنش ماکسیمم (τ_max) نه تنها بزرگ‌ترین برشی موجود در جانِ تیر بلکه بزرگ‌ترین تنش برشی موجود در تمام نقاط سطح مقطع محسوب می‌شود.

نیروی برشی موجود در جان

نیروی برشی عمودی وارد شده بر جانِ تیر را می‌توان با ضرب مساحت زیر نمودار تنش برشی در ضخامت جان (t) به دست آورد. نمودار تنش برشی شامل یک بخش مستطیلی با مساحت h₁τ_min و یک بخش سهمی‌وار با مساحت زیر تشکیل می‌شود:

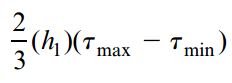
با جمع مساحت دو بخش مذکور و ضرب نتیجه آن در ضخامت جان و ترکیب کردن عبارت‌ها، رابطه نیروی برشی کل برای جانِ تیر تعیین می‌شود:

برای تیرهای بال پهن معمول، نیروی برشی موجود در جان 90 تا 98 درصد کل نیروی برشی موجود در سطح مقطع است. باقی این نیروها توسط بال‌های تیر تحمل می‌شوند. به دلیل سهم بالای جانِ تیر در تحمل نیروی برشی، طراحان در اغلب موارد با تقسیم نیروی برشی کل بر مساحت جان، مقدار تقریبی تنش برشی ماکسیمم را محاسبه می‌کنند. نتیجه این محاسبات، تنش برشی میانگین در جانِ تیر خواهد بود:

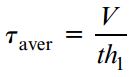
معمولاً در تیرهای بال پهن، مقدار تنش میانگین بین 10± تنش برشی ماکسیمم حاصل از رابطه بالا قرار می‌گیرد. از این‌رو، رابطه بالا می‌تواند به عنوان یک روش راحت برای تخمین تنش برشی ماکسیمم در نظر گرفته شود.

محدودیت‌های محاسبه تنش‌های برشی

روابط ابتدایی معرفی شده در این مقاله برای تعیین تنش‌های برشی عمودی موجود در جانِ یک تیر بال پهن قابل استفاده هستند. اگرچه، در هنگام ارزیابی این تنش‌ها در بال تیر دیگر نمی‌توان مقدار تنش‌های برشی بر روی عرض مقطع (عرض b بال‌ها) را ثابت در نظر گرفت. از این‌رو، برای این نواحی نمی‌توان از رابطه برش به منظور تعیین تنش‌های برشی استفاده کرد.

محل اتصال جان به بال بالایی تیر در y₁=h₁/2 را در نظر بگیرید. عرض سطح مقطع در این محل به طور ناگهانی از t به b تغییر می‌کند. تنش‌های برشی موجود بر روی سطوح آزاد ab و cd باید برابر با صفر باشد؛ در حالی که مقدار این تنش‌ها در خط bc برابر τ_min است. این مشاهدات نشان می‌دهند که توزیع تنش‌های برشی در محل اتصال جان و بال بسیار پیچیده بوده و توسط روش‌های ابتدایی قابل ارزیابی نیست.

فیلم آموزش مقاومت مصالح ۲ + مفاهیم کلیدی در فرادرس

کلیک کنید

علاوه بر این، تحلیل تنش در ماهیچه‌های تیر (گوشه‌های b و c در مثال بالا) نیز از پیچیدگی بالایی برخوردار است. ماهیچه‌های موجود در تیرهای بال پهن به منظور جلوگیری از افزایش بسیار زیاد تنش‌ها در نواحی مذکور به کار برده می‌شوند. به علاوه، این ماهیچه‌ها توزیع تنش بر روی جانِ تیر را نیز تغییر می‌دهند.

با توجه به نکات ارائه شده، رابطه برش برای تعیین تنش‌های برشی عمودی موجود در بال‌های تیر قابل استفاده نیستند. با این وجود، این رابطه نتایج قابل قبولی از تنش‌های برشی افقی موجود در این بخش‌ها را ارائه می‌دهد. روش معرفی شده برای تعیین تنش‌های برشی موجود در جان تیرهای بال پهن، برای مقاطعی با جانِ نازک نیز قابل استفاده است (مثال دوم این مقاله).

مثال‌های کاربردی

در این بخش، به منظور آشنایی با نحوه از استفاده از روابط ارائه شده برای تحلیل تنش‌های برشی موجود در تیرهای بال پهن و سازه‌های مشابه (مانند تیرهای T شکل)، به تشریح دو مثال کاربردی می‌پردازیم.

مثال 1

یک تیر بال پهن مطابق شکل زیر در معرض نیروی برشی عمودی V=45kN قرار گرفته است. اگر ابعاد سطح مقطع این تیر برابر با b=165mm ،t=7.5mm ،h=320mm و h₁=290mm باشد، تنش برشی ماکسیمم، تنش برشی مینیمم و نیروی برشی کل در جانِ تیر چقدر خواهد بود؟ (از نواحی ماهیچه‌ها صرف‌نظر کنید.)

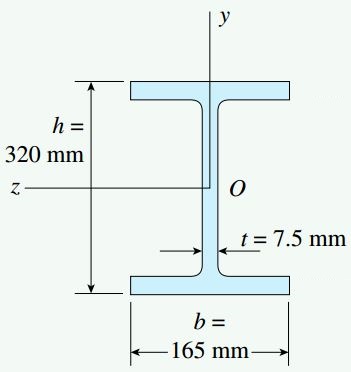
تنش‌های برشی ماکسیمم و مینیمم

برای تنش‌های برشی ماکسیمم و مینیمم موجود در جان تیر با استفاده از روابط معرفی شده در این مقاله، ابتدا باید ممان اینرسی سطح مقطع تیر را محاسبه کنیم:

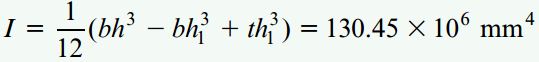
اکنون با جایگذاری مقدار I به همراه دیگر مقادیر عددی نیروی برشی V و ابعاد سطح مقطع، داریم:

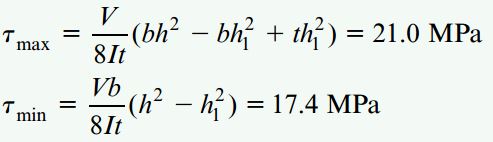
با توجه به نتایج بالا، نسبت τ_max به τ_min برابر 1.21 (تنش ماکسیمم در جان تیر 21 درصد بیشتر از تنش مینیمم) است. نمودار زیر، تغییرات تنش‌های برشی بر روی ارتفاع h₁ را نمایش می‌دهد.

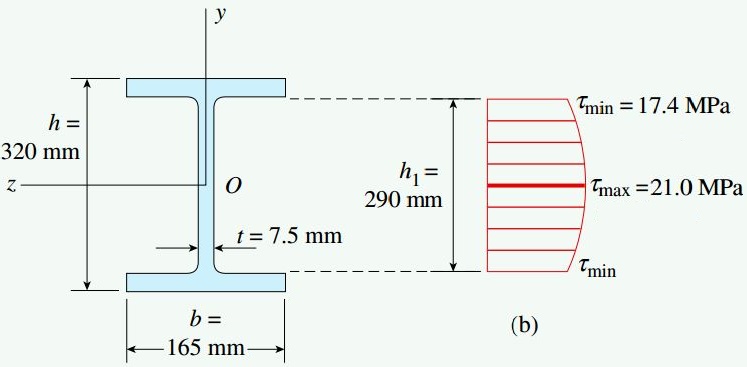
نیروی برشی

نیروی برشی موجود در جانِ تیر به صورت زیر محاسبه می‌شود:

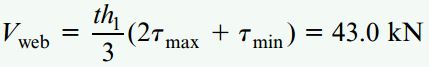
توجه داشته باشید که بر اساس این مقدار، جانِ تیر مورد بررسی در مقابل 96 درصد از کل نیروی برشی مقاومت می‌کند (نیروی برشی کل برابر 45 کیلو پاسکال است). به علاوه، میانگین تنش برشی موجود در جان نیز از رابطه زیر به دست می‌آید:

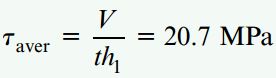
این مقدار تنها 1 درصد از تنش ماکسیمم کمتر است.

مثال 2

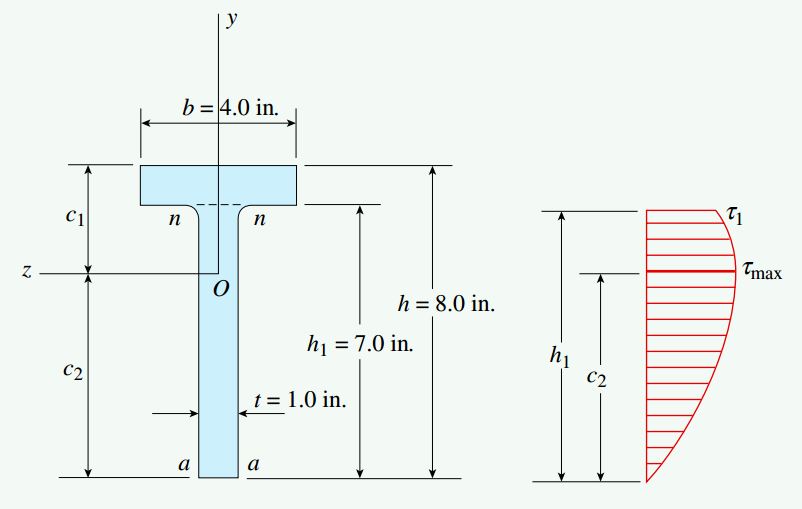
شکل زیر، یک تیر با سطح مقطع T شکل را نمایش می‌دهد که در معرض نیروی برشی عمودی V=10000lb قرار دارد. ابعاد سطح مقطع این تیر برابر b=4in ،t=1in ،h=8in و h₁=7in است.

فیلم آموزش مقاومت مصالح – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

با توجه به اطلاعات مسئله، تنش برشی τ₁ در بالای جانِ تیر (سطح nn) و تنش برشی ماکسیمم τ_max را تعیین کنید (از نواحی دارای ماهیچه صرف‌نظر شود).

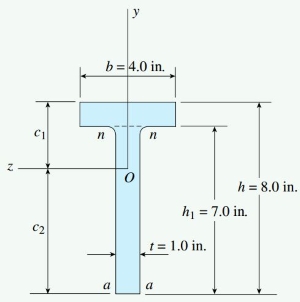
تعیین محل قرارگیری محور خنثی

محور خنثی تیر T در فاصله‌های c₁ و c₂ از بالا و پایین مرکز هندسی سطح مقطع آن قرار دارد. به منظور تعیین محل قرارگیری این محور، ابتدا باید سطح مقطع را به دو مستطیل مجزا (بال و جان) تقسیم کنیم. سپس، گشتاور اول Q_aa این دو مستطیل را نسبت به خط aa در پایین تیر به دست آوریم. فاصله c₂ با حاصل تقسیم Q_aa بر مساحت کل سطح مقطع A برابر است. به این ترتیب داریم:

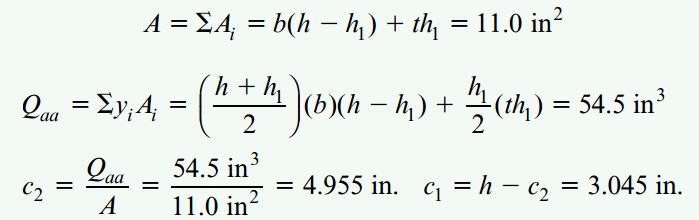
ممان اینرسی

به منظور تعیین ممان اینرسی I سطح مقطع نسبت به محور خنثی، ممان اینرسی I_aa حول خط aa در پایین تیر را تعیین کرده و سپس از تئوری محور موازی استفاده می‌کنیم. بر اساس تئوری محور موازی، ممان اینرسی یک سطح نسبت به هر محور بر روی صفحه دربرگیرنده آن، با ممان اینرسی سطح نسبت به یک محور مرکزی موازی به علاوه حاصل‌ضرب مساحت در مربع فاصله بین دو محور برابر است.

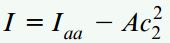
به این ترتیب:

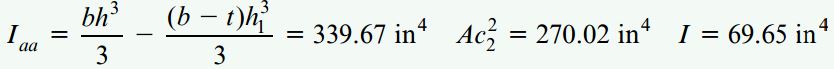
تنش برشی در بالای جان

برای یافتن تنش برشی τ₁ در بالای جانِ تیر، گشتاور اول Q₁ سطح بالای خط nn را محاسبه می‌کنیم. این گشتاور اول با مساحت بال در فاصله مرکز هندسی آن تا محور خنثی برابر است:

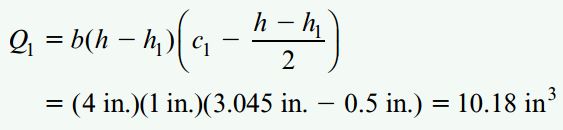
اگر به جای رابطه بالا از مساحت زیر خط nn استفاده می‌کردیم، نتیجه به دست آمده با مقدار بالا یکسان می‌شد:

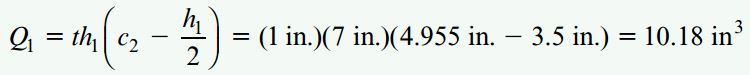
با جایگذاری مقدار Q₁ در رابطه برش داریم:

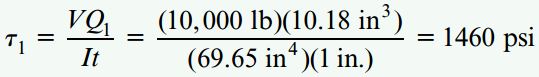
این تنش هم به صورت تنش برشی عمودی بر روی سطح مقطع تیر و هم به صورت تنش برشی افقی بر روی سطح افقی میان بال و جان اعمال می‌شود.

تنش برشی ماکسیمم

تنش برشی ماکسیمم در جان تیر بر روی محور خنثی رخ می‌دهد. از این‌رو، در ابتدا باید گشتاور اول Q_max برای سطح مقطع زیر محور خنثی را محاسبه کنیم:

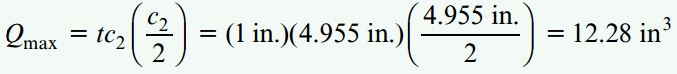
با محاسبه گشتاور اول سطح بالای محور خنثی، نتیجه مشابه ای به دست خواهد آمد اما حجم محاسبات بیشتر خواهد بود. اکنون مقدار Q_max را درون رابطه برش قرار می‌دهیم:

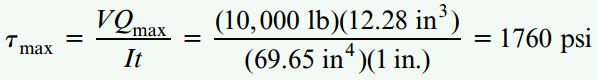
این مقدار، تنش برشی ماکسیمم درون تیر را نمایش می‌دهد. نحوه توزیع تنش‌های برشی درون جان تیر در شکل زیر نشان داده شده است.

^^