تحلیل داده های چند بعدی در پایتون — راهنمای کاربردی

«تحلیل دادههای چند بعدی» (Multidimensional Data Aanalysis)، نوع مهم و مفیدی از تحلیلها است که امروزه با توجه به افزایش حجم و البته، ابعاد دادهها، از اهمیت به سزایی برخوردار است. در این نوع از تحلیلها، روابط گوناگون موجود میان متغیرها و به طور کل، دادهها، در نظر گرفته میشوند. در ادامه، برخی از روشهای تحلیل داده های چند بعدی در پایتون مورد بررسی قرار میگیرد.
مجموعه داده مورد استفاده برای تحلیل دادههای چند بعدی و چند متغیره
مجموعه دادهای که در این مطلب برای تحلیل داده های چندبُعدی در پایتون مورد استفاده قرار گرفته است، «Zoo Data Set» نام دارد.
مشخصات این مجموعه داده در جدول زیر ارائه شده است.
| خصیصه مجموعه داده | چند متغیره |
| نوع ویژگیها | دستهای، صحیح |
| نوع وظیفه مربوطه | دستهبندی |
| تعداد نمونهها | ۱۰۱ |
| تعداد ویژگیها | ۱۷ |
| حاوی مقادیر ناموجود؟ | خیر |
این مجموعه داده را میتوان از اینجا دانلود کرد.
تحلیل داده های چند بعدی در پایتون
در راستای انجام تحلیل، ابتدا باید مجموعه داده را «وارد» (Import | ایمپورت) کرد.
بدین منظور، میتوان از قطعه کد زیر استفاده کرد.
1import pandas as pd
2
3zoo_data = pd.read_csv("zoo_data.csv", encoding = 'utf-8',
4 index_col = ["animal_name"])
5
6# print first 5 rows of zoo data
7print(zoo_data.head())خروجی قطعه کد بالا، به صورت زیر است.

نکته: نوع ویژگیهایی که در این مجموعه داده وجود دارند، معمولا «دستهای» (Categorical) هستند. روش مورد استفاده در این مطلب برای تحلیل دادههای دستهای، بسیار ساده و قابل درک است و تفسیر و پیادهسازی آن نیز آسان خواهد بود. روش مورد استفاده در این مطلب، شامل «تحلیل همبستگی» (Correlation Analysis)، «تحلیل مولفه اساسی» (Principal Component Analysis | PCA) و «تحلیل داده اکتشافی» (Exploratory Data Analysis | EDA) میشود.
تحلیل خوشه
با توجه به آنکه دادههای موجود بر مبنای ویژگیهای انواع مختلف حیوانات است، میتوان حیوانات را در گروههای گوناگون (خوشهها) یا زیرگروههایی با استفاده از روشهای خوشهبندی شناخته شدهای مانند «K-میانه» (K-Means)، «خوشهبندی سلسله مراتبی» (Hierarchical Clustering) و «K-نزدیکترین همسایگی» (K-Nearest Neighbours | KNN) دستهبندی کرد.
به منظور حفظ سادگی، به نظر میرسد که خوشهبندی K-Means در این مثال گزینه مناسبتری باشد. خوشهبندی دادهها با استفاده از روش خوشهبندی K-Means با استفاده از ماژول KMeans از cluster class از کتابخانه پایتون «سایکیتلِرن» (Scikit-Learn) انجام میشود. قطعه کد مورد استفاده در این راستا، در ادامه آمده است.
1# from sklearn.cluster import KMeans
2clusters = 7
3
4kmeans = KMeans(n_clusters = clusters)
5kmeans.fit(zoo_data)
6
7print(kmeans.labels_)خروجی قطعه کد بالا، به صورت زیر است.

در اینجا، اینرسی کلی خوشه برابر با 119.70392382759556 است. این مقدار در متغیر kmeans.inertia_ ذخیره شده است.
تحلیل EDA
برای انجام تحلیلهای EDA، نیاز به کاهش ابعاد دادههای چند متغیره موجود به دادههای دوبُعدی و سهبُعدی وجود دارد. برای رسیدن به این مقصود، میتوان از «تحلیل مولفه اساسی» (Principal Component Analysis | PCA) استفاده کرد.
برای اعمال PCA، میتوان از PCA module از class decomposition، از کتابخانه sklearn به صورت زیر استفاده کرد.
1# from sklearn.decomposition import PCA
2
3pca = PCA(3)
4pca.fit(zoo_data)
5
6pca_data = pd.DataFrame(pca.transform(zoo_data))
7
8print(pca_data.head())خروجی قطعه کد بالا، به صورت زیر است.

خروجی داده بالا، نشانگر دادههای کاهش یافته به سهبُعد است که میتوان تحلیل EDA را روی آنها انجام داد.
نکته: دادههای کاهش یافته تولید شده به وسیله PCA را میتوان به طور غیر مستقیم برای انجام انواع گوناگونی از تحلیلها استفاده کرد؛ اما این دادهها به طور مستقیم توسط انسان قابل تفسیر نیستند.
نمودار نقطهای، یک نمودار دوبُعدی/سهبُعدی است که برای تحلیل خوشههای گوناگون در دادههای دوبُعدی/سهبُعدی مفید هستند. نمودار نقطهای سهبُعدی دادههایی که پیش از این تولید شدهاند را میتوان با استفاده از روشی که در ادامه بیان شده است، ترسیم کرد.
کد زیر یک کد «پایتونیک» (Pythonic) است که آرایهای از رنگهای مرتب شده بر اساس رنگ، مقدار و اشباع آنها را تولید میکند. در این نمودار نقطهای، که در آن تعداد رنگها تقریبا برابر با تعداد خوشهها است. در اینجا، هر رنگ، به یک خوشه تخصیص یافته و برای مشخص کردن یک حیوان به عنوان یک نقطه در هنگام ترسیم آن در یک نمودار/فضای سهبُعدی است (در این مثال، نمودار نقطهای).
1from matplotlib import colors as mcolors
2import math
3
4''' Generating different colors in ascending order
5 of their hsv values '''
6colors = list(zip(*sorted((
7 tuple(mcolors.rgb_to_hsv(
8 mcolors.to_rgba(color)[:3])), name)
9 for name, color in dict(
10 mcolors.BASE_COLORS, **mcolors.CSS4_COLORS
11 ).items())))[1]
12
13
14# number of steps to taken generate n(clusters) colors
15skips = math.floor(len(colors[5 : -5])/clusters)
16cluster_colors = colors[5 : -5 : skips] کد زیر یک کد پایتونیک است که یک نمودار نقطهای سهبُعدی را تولید میکند که در آن، هر نقطه داده دارای یک رنگ مرتبط به خوشه متناظر آن است.
1from mpl_toolkits.mplot3d import Axes3D
2import matplotlib.pyplot as plt
3
4fig = plt.figure()
5ax = fig.add_subplot(111, projection = '3d')
6ax.scatter(pca_data[0], pca_data[1], pca_data[2],
7 c = list(map(lambda label : cluster_colors[label],
8 kmeans.labels_)))
9
10str_labels = list(map(lambda label:'% s' % label, kmeans.labels_))
11
12list(map(lambda data1, data2, data3, str_label:
13 ax.text(data1, data2, data3, s = str_label, size = 16.5,
14 zorder = 20, color = 'k'), pca_data[0], pca_data[1],
15 pca_data[2], str_labels))
16
17plt.show()خروجی قطعه کد بالا، به صورت زیر است.
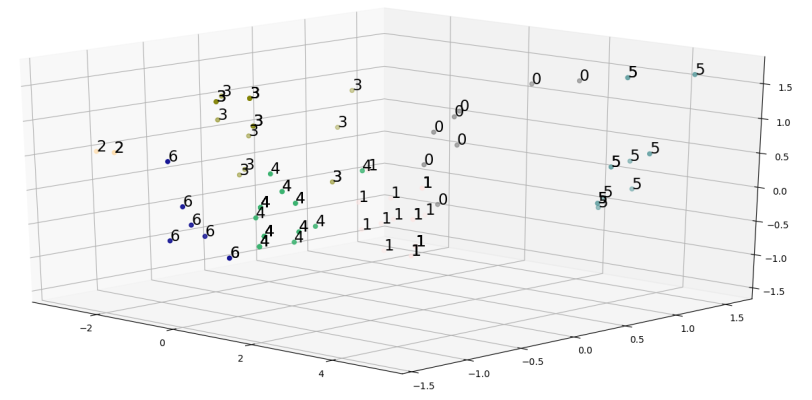
تحلیل دقیق نمودار نقطهای میتواند به این نظریه بیانجامد که خوشههای شکل گرفته با استفاده از دادههای اولیه، قدرت بیان کافی را ندارند. برای حل این مشکل، نیاز به کاهش دادهها به دادههایی است که میتوانند خوشههای مفیدی تولید کنند. یک راه برای تولید چنین ویژگیهایی، انجام تحلیل همبستگی است. این کار را میتوان با ترسیم نمودار «نقشه گرمایی» (Heatmap) و «سطحی سهبُعدی» (Trisurface) انجام داد. در این راستا، میتوان از قطعه کد زیر استفاده کرد.
1import seaborn as sns
2
3# generating correlation heatmap
4sns.heatmap(zoo_data.corr(), annot = True)
5
6# posting correlation heatmap to output console
7plt.show()خروجی قطعه کد بالا به صورت زیر است.
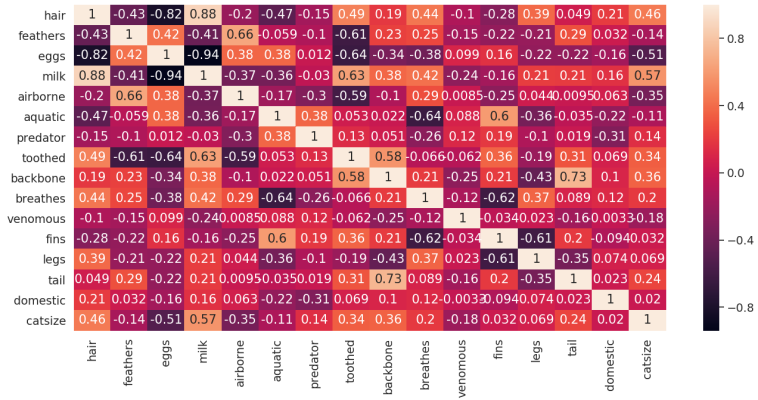
کد زیر برای تولید یک نمودار سطحی سهبُعدی از «ماتریس همبستگی» (Correlation Matrix) با ساخت لیستی از تاپلها که در آنها یک تاپل حاوی مقادیر مختصات و همبستگی به ترتیب اسامی حیوانات است، مورد استفاده قرار میگیرد. «شبهکد» (Psuedocode) مورد استفاده برای این کار در زیر آمده است.
# PsuedoCode
tuple -> (position_in_dataframe(feature1),
position_in_dataframe(feature2),
correlation(feature1, feature2))
کد مورد استفاده برای ترسیم نمودار سطحی سهبُعدی ماتریس همبستگی به صورت زیر است.
1from matplotlib import cm
2
3# generating correlation data
4df = zoo_data.corr()
5df.index = range(0, len(df))
6df.rename(columns = dict(zip(df.columns, df.index)), inplace = True)
7df = df.astype(object)
8
9''' Generating coordinates with
10corresponding correlation values '''
11for i in range(0, len(df)):
12 for j in range(0, len(df)):
13 if i != j:
14 df.iloc[i, j] = (i, j, df.iloc[i, j])
15 else :
16 df.iloc[i, j] = (i, j, 0)
17
18df_list = []
19
20# flattening dataframe values
21for sub_list in df.values:
22 df_list.extend(sub_list)
23
24# converting list of tuples into trivariate dataframe
25plot_df = pd.DataFrame(df_list)
26
27fig = plt.figure()
28ax = Axes3D(fig)
29
30# plotting 3D trisurface plot
31ax.plot_trisurf(plot_df[0], plot_df[1], plot_df[2],
32 cmap = cm.jet, linewidth = 0.2)
33
34plt.show()خروجی قطعه کد بالا به صورت زیر است.

با استفاده از نمودار گرمایشی و سطحی سهبُعدی، میتوان استدلالهایی پیرامون چگونگی انتخاب یک مجموعه کوچکتر از ویژگیهای مورد استفاده برای انجام تحلیل خوشه داشت. به طور کلی، جفت ویژگیها با مقادیر همبستگی بالا، دارای قدرت بیان بالایی هستند و میتوان از آنها برای تحلیلهای بیشتر استفاده کرد.
در این مثال، با نگاهی به هر دو نمودار، میتوان به یک لیست عقلانی از هفت ویژگی [“milk”, “eggs”, “hair”, “toothed”, “feathers”, “breathes”, “aquatic”] رسید. با اجرای مجدد تحلیل خوشه روی زیرمجموعه مجموعه ویژگیها، میتوان نمودار نقطهای با استلال بهتر پیرامون چگونگی توزیع حیوانات مختلف در میان گروههای گوناگون را به دست آورد.

در اینجا، شاهد یک اینترسی خوشه کاهش یافته به 14.479670329670329 هستیم که در واقع بسیار کمتر از اینرسی اولیه است.
اگر نوشته بالا برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای آمار، احتمالات و دادهکاوی
- آموزش هوش مصنوعی
- مجموعه آموزشهای برنامه نویسی پایتون (Python)
- داده کاوی (Data Mining) — از صفر تا صد
- یادگیری علم داده (Data Science) با پایتون — از صفر تا صد
- معرفی منابع جهت آموزش یادگیری عمیق (Deep Learning) — راهنمای کامل
^^










