درک موج های سینوسی – به زبان ساده
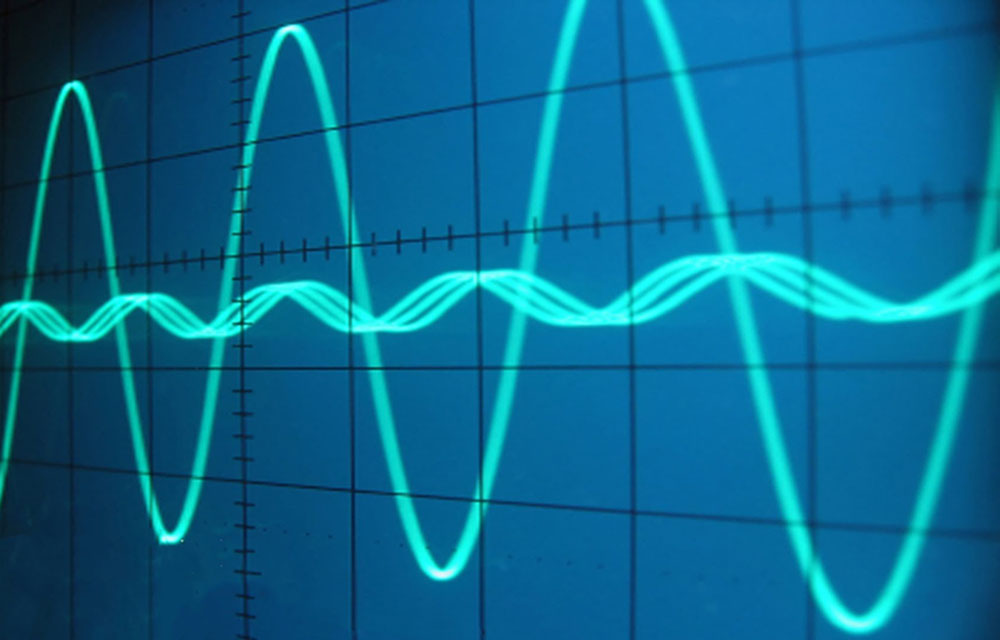
موجهای سینوسی باعث سردرگمی افراد زیادی میشوند. البته همه ما میتوانیم برخی از فرمولهای مثلثات را به خاطر آورده و خطوطی را روی مثلثها ترسیم کنیم. اما آیا معنی دقیق این خطوط را میدانیم؟ شاید بهتر باشد که سینوس را از شکلهای دیگر به جز مثلث نیز استخراج کنیم. در ادامه یک گفتگوی خیالی در کلاس هندسه بین معلم و دانشآموز ارائه شده است که شاید از جنبههای مختلفی واقعیت دارد:
- معلم: هندسه به توضیح شکلها، خط و موارد این چنین میپردازد.
- دانشآموز: لطفاً یک خط به من نشان دهید.
- معلم: (نگاهی به اطراف میکند) ... آن آجر را میبینید؟ لبه آن آجر یک خط محسوب میشود.
- دانشآموز: پس خطوط بخشی از یک شکل هستند.
- معلم: بله چنین است. اغلب شکلها خطوطی دارند. اما خود خط، مفهومی مستقل است: مانند یک خط از پرتوی نور، یک مسیر روی نقشه یا ...
- دانشآموز: آجرها خط دارند، خطها از آجرها میآیند. آجر ... آجر... آجر.
سناریوی فوق در اغلب کلاسهای ریاضیات به وقوع میپیوندد. برای نمونه دایرهها سینوس دارند. سینوسها از دایرهها میآیند. دایره ... دایره ... دایره.
باید تأکید کنیم که دایرهها یکی از مثالهای سینوس هستند. به بیان دیگر سینوس به طور طبیعی منحنی است که نشانگر نرمی و همواری است. به همان ترتیب که خطوط، باعث گوشهدار شدن مربع میشوند سینوسها نیز باعث گرد شدن دایره میشوند.
اجازه بدهید ابتدا با مشاهده شکل خود سینوس، شهودمان را تقویت کنیم و سپس شروع به درک شیوه تطبیق آن با دایره و موارد مشابه بکنیم.
سینوس در برابر خطوط
به خاطر داشته باشید که همواره باید ایده را از مثال جدا کنیم. برای نمونه مربعها مثالی از خطوط هستند. سینوسها نیز زمانی درک میشوند که خود ایدهای مستقل باشند و نه بخشی از یک دایره.
در نمودار زیر سینوس را در یک شبیهساز مشاهده میکنید:
- روی استارت کلیک کنید: با کلیک روی استارت، دایره فوق را میبینید که با حرکتی نرم به سمت بالا و پایین حرکت میکند. این یک موج سینوسی است که منشأ حرکتهای طبیعی زیادی مانند جهش فنر، حرکت آونگ، لرزش ریسمان و بسیاری از چیزهای دیگر است.
- حالت عمودی «Vertical» را به خطی «linear» تغییر دهید: تفاوت بزرگی مشاهده میشود. اینک میبینید که حرکت حالتی ثابت و روباتیک یافته است.
توضیح به صورت زیر است:
- حرکت خطی: در این حالت سرعت حرکت ثابت است. شیء متحرک با سرعت ثابتی حرکت میکنند و جهت خود را تغییر میدهند. این یک حرکت روباتیک و غیرطبیعی است.
- حرکت سینوسی: در این حالت سرعت حرکت متغیر است. ابتدا سریع آغاز میشود، سپس کندتر شده و متوقف میشود و دوباره سرعت میگیرد.
متأسفانه در کتب درسی، سینوس با استفاده از انیمیشن یا حرکت توضیح داده نمیشود؛ بلکه در اغلب موارد سینوس با استفاده از یک تایملاین (محور افقی زمان را نشان میدهد) معرفی میشود.
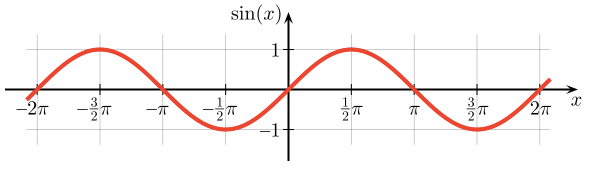
این همان نمودار مشهوری است که در اغلب موارد مشاهده میکنیم. آیا این نمودار ثابت معنی و مفهوم سینوس را نمایش میدهد؟ در واقع همانقدر که مشاهده اسکلت یک گربه، میزان چابکی را نشان میدهد! ابتدا باید حرکت سینوسی را مشاهده کرد و سپس اقدام به ترسیم نمودار آن کرد.
دایره گریز ناپذیر
دایرهها سینوس دارند، این مطلب سخن درستی است؛ اما این که سینوس را به دایرهها منحصر کنیم، مانند این است که فکر کنیم تخممرغها فقط داخل املت یافت میشوند.
کمی بیشتر توضیح میدهیم. در شبیهسازی فوق، وضعیت شیء متحرک را روی vertical:none و *horizontal:sine قرار دهید. در این حالت حرکتی دوبعدی را مشاهده میکنید که همان حرکت سینوسی است. نکته ظریفی وجود دارد. به طور معمول سینوس از نیمه چرخه طبیعی خود آغاز میشود و تا حد بیشینه بالا میرود. این بار ما از بیشینه فوقانی آغاز میکنیم و به سمت نیمه پایین میآییم. سینوسی که از بیشینه مقدار آغاز شود کسینوس نامیده میشود. کسینوس صرفاً نسخه دیگری از سینوس است، همانطور که خط افقی نسخهای از خط عمودی است.
اگر از هر دو موج سینوسی استفاده کنیم یعنی حرکت عمودی را روی sine و حرکت افقی را روی *sine قرار دهیم، میبینیم که حرکت شیء متحرک منجر به ترسیم یک دایره میشود.
در واقع ترکیب حرکت جهشی افقی و عمودی منجر به حرکت دایرهای میشود. در اغلب کتابهای درسی، ابتدا دایره ترسیم میکنند و سپس تلاش میکنند از آن سینوس دربیاورند؛ اما بهتر است ابتدا حرکت افقی و عمودی موج سینوسی معرفی شود و سپس این دو با هم ترکیب شوند.
در ادامه چند مفهوم مهم که از سینوس به دست میآیند را ارائه کردهایم:
سینوس در واقع 1 بُعدی است
سینوس در یک بُعد نوسان میکند. شاید از این حرف تعجب کنید، چون ما در اغلب موارد سینوس را در برابر زمان ترسیم میکنیم و گاهی اوقات شیئی که حرکت سینوسی دارد در دو بعد حرکت میکند؛ اما این وضعیت اختیاری است. فنر یکبعدی است و به خوبی موج سینوسی را نشان میدهد.
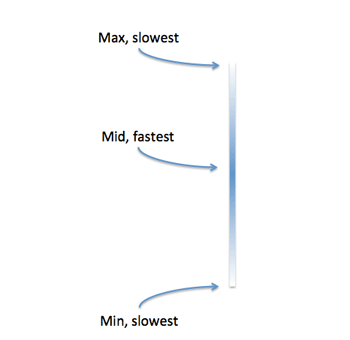
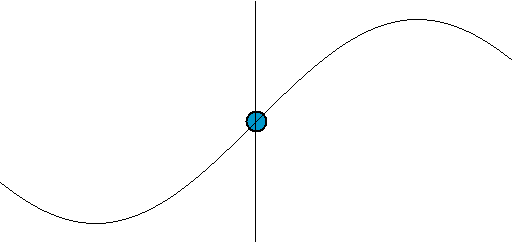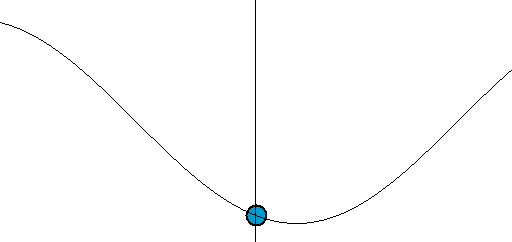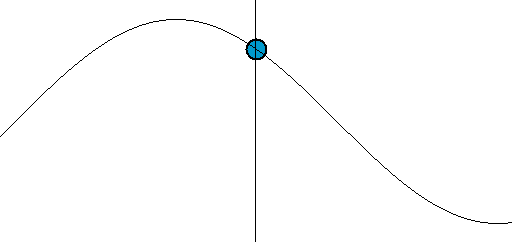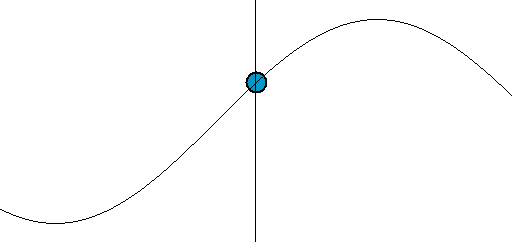
دایرهها نمونهای از دو موج سینوسی هستند
دایرهها و مربعها ترکیبی از اجزای پایهای (به ترتیب سینوسها و خطوط) هستند. دایره از دو موج 1 بعدی تشکیل یافته است که یکی در جهت افقی و دیگری عمودی حرکت میکند.
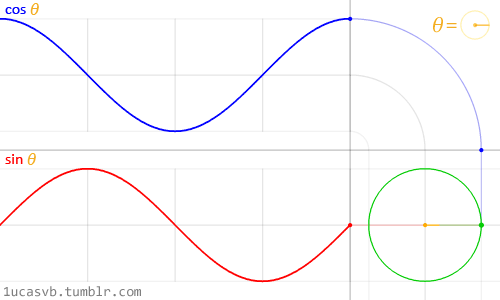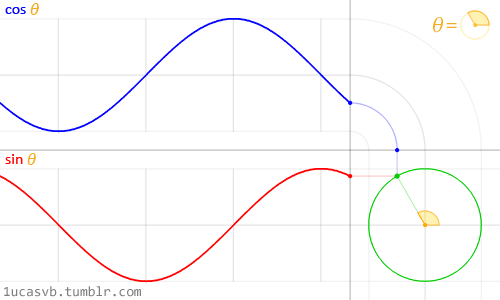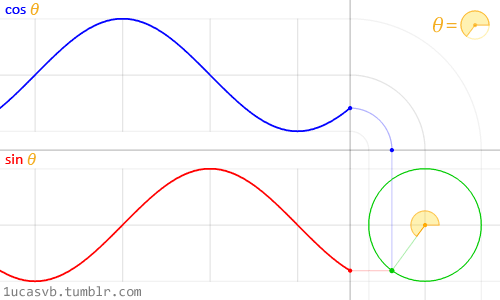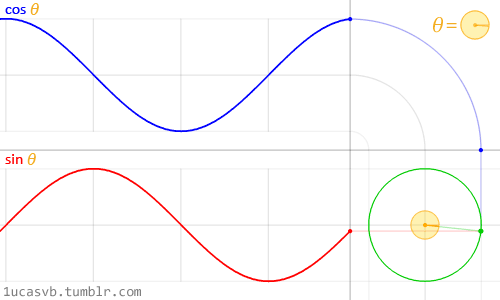
اما به خاطر داشته باشید که دایرهها منشأ سینوسها نیستند؛ همانطور که مربعها منشأ خطوط محسوب نمیشوند. اینها تنها مثال هستند و نه منبع.
مقادیر سینوس به چه معنی هستند؟
چرخههای سینوسی بین 1- و 1 هستند. مقدار سینوس از 0 آغاز میشود و تا 1.0 (بیشینه) بالا میرود، سپس تا 1- (کمینه) پایین میآید و دوباره به مقدار صفر بازمیگردد. سینوس را میتوان نوعی درصد نیز دانست که از 100% (حرکت با نهایت سرعت به جلو) تا 100-% (عقبنشینی با بیشترین سرعت) تغییر میکند.
منظور از مقدار ورودی x در (sin(x چیست؟
این سؤال دشواری است. سینوس یک چرخه است و x یعنی ورودی میزان حرکت ما در چرخه را مشخص میکند. شاید مقایسه با خطوط این معنی را بهتر مشخص سازد.
- فرض کنید روی یک مربع حرکت میکنید که هر ضلع آن 10 ثانیه طول میکشد.
- پس از 1 ثانیه، شما 10% از طول یک ضلع مربع را پیمودهاید.
- پس از 5 ثانیه، 50% ضلع مربع را طی کردهاید.
- پس از 10 ثانیه شما یک ضلع مربع را به پایان بردهاید.
حرکت خطی چندان شگفتانگیز نیست. اما در مورد سینوس (با تمرکز روی بخش 0 تا بیشینه):

- اگر روی یک موج سینوسی حرکت کنیم، از 0 (خنثی) تا 1.0 (بیشینه) را طی میکنیم که 10 ثانیه طول میکشد.
- پس از 5 ثانیه 70% مسیر را پیمودهایم، چون موج سینوسی با سرعت بالا شروع میشود و سپس حرکت کندتر میشود. اکثر مسیر در نیمه نخست 5 ثانیهای پیموده شده است.
- رسیدن از 70% به 100%، 5 ثانیه طول میکشد. در واقع رسیدن از 98% به 100% خودش یک ثانیه طول میکشد!
در حرکت سینوسی علیرغم سرعت اولیه زیاد، هنگام رسیدن به نقطه بیشینه، سرعت کاملاً کند میشود و در واقع لمس بسیار ملایمی با نقطه بیشینه دارد و سپس میچرخد. این همواری باعث میشود که سینوس، سینوس شود.
در نمودار شبیهسازی ابتدای این مقاله اگر دکمه «show stats» را بزنید، درصد کامل شدن چرخه کلی، چرخه کوچک (0 تا 1.0)، و مقدار به دست آمده در هر لحظه را مشاهده میکنید. سپس نمودار را متوقف کنید و بین حرکت خطی و سینوسی برای مشاهده مقدار سوئیچ کنید.
اینک سؤال این است که 10% از یک چرخه خطی بیشتر است یا 10% از چرخه سینوس؟ در مورد سینوس میدانیم که در ابتدا با سرعت بالایی آغاز میشود. زمانی که سینوس 50% چرخه را طی میکند، با سرعت میانگین چرخه خطی حرکت میکند و پس از آن کندتر میشود، تا این که به بیشینه میرسد و میچرخد.
پس دانستیم که x مقدار طی شده در چرخه است، اما چرخه چیست؟
چرخه به زمینه موضوعی بستگی دارد.
- در مثلثات مقدماتی x درجه است و چرخه کامل 360 درجه است.
- در مثلثات پیشرفته x رادیان است و یک چرخه کامل یعنی دور زدن یک دایره معادل 2*pi radian است.
باز هم میبینیم که چرخهها به دایرهها وابسته هستند، اما آیا میتوان از دایرهها گریزی یافت؟
عدد پی بدون تصویر
فرض کنید با فردی فاقد قوه بینایی مواجه هستید که تنها میتواند متوجه فرق روشنایی و تاریکی شود. آیا میتوان پی را برای او توضیح داد؟ مسلماً توضیح محیط یک دایره به وی کار دشواری خواهد بود.
اما میتوانیم سینوس را به صورت یک الگوی تکرارشونده معرفی کنیم، یعنی چرخهای که تکرار میشود از 0 تا 1، تا 0، تا 1-، تا 0 و همین طور تا آخر.
فرض کنید مقدار پی را به صورت زمانی تعریف کنیم که طول میکشد سینوس از 0 به 1 برود و به 0 بازگردد. اینک ما میتوانیم از عدد پی بدون اشاره به دایره استفاده کنیم. پی مفهومی است که غالباً در دایرهها استفاده میشود:
- سینوس یک حرکت نوسانی عقب/جلو است.
- پی زمانی است که سینوس از حالت خنثی به بیشینه رفته و به حالت خنثی بازمیگردد.
- n * Pi که به جای n میتوان اعداد 0، 1، 2 و ... قرار داد، زمانهایی هستند که شما در نقطه صفر (خنثی) قرار دارید.
- 2Pi، 4pi، 6pi و غیره چرخههای کامل هستند.
به همین دلیل است که پی در فرمولهای زیادی ظاهر میشود. بنابراین پی ربط مطلقی به دایرهها ندارد. در واقع پی موج سینوسی است که به مرکز بازمیگردد. دایره نمونهای از شکلی است که تکرار میشود و با گذر هر 2 پی واحد از زمان مجدداً به مرکز بازمیگردد. اما فنر، نوسان و حرکتهای دیگر نیز پس از پی مقدار به مرکز بازمیگردند.
اگر پی نیمی از چرخه طبیعی باشد، چرا یک عدد ساده و سر راست نیست؟
سؤال فوق را با یک سؤال دیگر میتوان پاسخ داد. چرا مربع 1×1 قطری برابر با = 1.414... دارد که عددی گنگ است؟
زمانی که طبیعت با سیستم اعداد ناسازگار است، باعث ناخوشنودی فلسفی میشود. البته شهود مناسبی در این زمینه وجود ندارد. چون مربع 1×1 + قضیه فیثاغورس همچنان منجر به خروجیهای پیچیدهای میشود.
سینوس چه سرعتی دارد؟
قبلاً درجایی از نوشته گفتیم که فرض کنید سینوس در طی 10 ثانیه از 0 تا مقدار بیشینه میرسد و در بخش قبل نیز اشاره کردیم که پی ثانیه طول میکشد که سینوس از 0 به بیشینه رسیده و دوباره به صفر بازگردد. نتیجه این دو جمله این است که:
- (Sin(x موج سینوسی پیشفرض و آماده است که پی واحد از زمان برای رفتن از 0 به بیشینه و بازگشت به صفر نیاز دارد. به عبارت دیگر یک چرخه کامل 2 پی واحد از زمان طول میکشد.
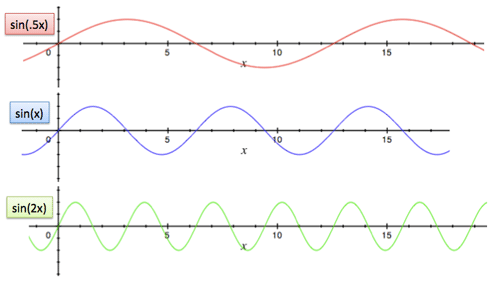
- (Sin(2x موجی است که با سرعت دو برابر حرکت میکند.
- (Sin(x/2 موجی ست که با نصف سرعت حرکت میکند.
بنابراین از (Sin(n*x برای سریعتر ساختن موج سینوسی به مقدار دلخواه استفاده میکنیم. در اغلب موارد عبارت «موج سینوسی» اشاره به شکل کلی سینوس دارد و نه سرعت خاص.
بخش دوم: درک تعریف سینوس
در این بخش تلاش میکنیم درکی شهودی از سینوس از طریق شیوه ارتباط تعاریف مختلف سینوس پیدا کنیم.
تعریف 1: ارتفاع یک مثلث/دایره
از آنجا که این تعریف نخستین بار در یک مثلث مشاهده شده است، احتمالاً شما نیز سینوس را این گونه به خاطر میآورید.

- سینوس: ضلع مقابل/ وتر
- کسینوس: ضلع مجاور / وتر
- تانژانت: ضلع مقابل / ضلع مجاور
در یک مثلث قائمالزاویه با زاویه x، مقدار (Sin(x طول ضلع مقابل، تقسیم بر وتر است. اگر وتر برابر با 1 باشد، روابط به فوق صورت زیر درمیآیند:
- سینوس = ضلع مقابل
- کسینوس = ضلع مجاور
و با اندکی زیرکی بیشتر، میتوانیم مثلثهایی را با وتر 1 روی دایرهای با شعاع 1 ترسیم کنیم:

میبینیم که دایره شامل همه مثلثهای قائمالزاویهی ممکن است. برای نمونه:
- sin(45) =.707
- اگر میلهای 10 متری را با زاویه 45 درجه از زمین نگهداریم، بر اساس روابط مثلثاتی میتوانیم محاسبه کنیم که ارتفاع نوک میله از زمین برابر با sin(45) × 10 = 7.07 متر است.
- ارتفاع یک میله 8 متری در چنین شرایطی برابر با sin(45) × 8 = 5.65 متر خواهد بود.
این محاسبات مستقیم برای مهندسی و ساخت و ساز بسیار مفید هستند. متأسفانه ما پس از هزاران سال همچنان فکر میکنیم که سینوس به معنی ارتفاع مثلث است؛ در حالی که چنین نیست و در واقع سینوس نسبتی است که در دایرهها و مثلثها نیز ظاهر میشود.
اگر واقعبینانه نگاه کنیم در اغلب مسائل به سراغ مثلثات میرویم و سینوس را برابر با ارتفاع تصور میکنیم تا مسئله به سرعت حل شود. در این رویکرد مشکلی نیست؛ اما نباید در این سطح متوقف شد.
تعریف 2: سریهای نامتناهی
شاید برای شما سؤال پیش آمده باشد که ماشین حساب چطور این قدر سریع سینوس را محاسبه میکند؟ آیا برای محاسبه آن دست به ترسیم دایره میزند؟ نه چنین نیست؛ بلکه از یک روش بی دایره برای محاسبه سینوس استفاده میکند:
- سینوس شتابی مخالف موقعیت کنونی شما دارد.
برای توضیح بیشتر از مثال حساب بانکی استفاده میکنیم. فرض کنید رئیس بدجنسی دارید که هر ماه میزان پاداش کاری شما را دقیقاً به اندازه معکوس موجودی حساب بانکیتان تعیین میکند. اگر یک میلیون تومان در حساب خود داشته باشید، در این صورت در ماه بعد، پاداش کاری شما برابر با 1- میلیون تومان خواهد بود. البته درآمد شما ممکن است 2 میلیون تومان در ماه باشد، بنابراین شما همچنان پولی دریافت میکنید (1-2 = 1 میلیون تومان برای این ماه)؛ اما در نهایت تراز حساب شما کاهش مییابد، زیرا از میزان درآمد شما بیشتر است.
اما جای ترس نیست، زمانی که موجودی حساب شما منفی شد (مثلاً 1- میلیون تومان) در این صورت رییستان 1 میلیون تومان در ماه پاداش به شما میدهد. در این حالت نیز درآمد میتواند منفی باشد؛ اما در نهایت پاداش حقوق از آن بیشتر خواهد بود.
کشش مداوم به سمت مرکز باعث میشود که چرخهای تشکیل شود. وقتی که موجودی افزایش مییابد، این کشش باعث میشود موجودی کاهش یابد، همچنین نشان میدهد که چرا سینوس در حالت خنثی، بالاترین سرعت را دارد. اگر در موقعیت بیشینه باشید، شروع به سقوط میکنید و همزمان با پایین آمدن پاداشهای منفی بیشتر و بیشتری کسب میکنید. زمانی که از حد خنثی عبور میکنید، همه پاداشهای منفی را جمع کردهاید و این بار پاداشهای مثبت دریافت میکنید و رفتهرفته روند منفی کندتر میشود.
بدین ترتیب سینوس همان روند شتابگیری معکوس موقعیت شما محسوب میشود و از آنجا که دایره از یک سینوس افقی و یک سینوس عمودی تشکیل یافته است. حرکت دایرهای را میتوان «یک کشش مداوم معکوس موقعیت کنونی به سمت مرکز عمودی و افقی دانست».
توضیح سینوس به کمک حسابان
سینوس را نیز مانند عدد e میتوان به تأثیرهای کوچکتر تقسیم کرد:
- متحرک، حرکت خود را از 0 آغاز میکند و با سرعت واحدی رشد میکند.
- در هر لحظه یک شتاب منفی آن را پس میکشد.
این تعریف را چطور میتوان تصور کرد؟ در بخش زیر تأثیر هر یک از تأثیرهای فوق بر فاصله متحرک از مرکز را توضیح دادهایم.
ضربه اولیه ما باعث افزایش خطی فاصله میشود: y (فاصله از مرکز) = x (زمان مورد نیاز)
در هر لحظه یک نیروی بازگرداننده x– حس میشود. هر دو را با هم ادغام میکنیم تا تأثیر شتابگیری معکوس بر مسافت را نیز لحاظ کنیم:
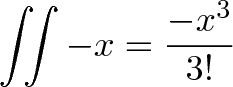
مشاهده تأثیر شتابگیری منفی بر مسافت مانند دیدن تأثیر پاداشهای منفی بر موجودی حساب بانکی است. این پاداش باعث تغییر در درآمد شما میشود، و درآمد شما باعث تغییر موجودی حساب بانکی میشود.
بنابراین پس از x ثانیه میتوانیم حدس بزنیم که سینوس x (ضربه اولیه) منهای !x^3/3 (تأثیر شتاب منفی) است:
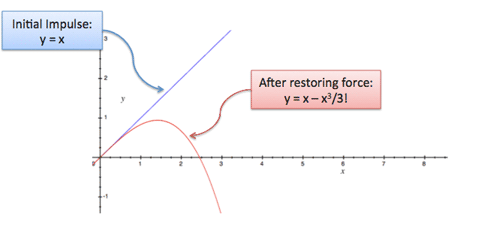
در نمودار فوق میبینیم که چیز نادرستی وجود دارد چون سینوس موجی نزولی نیست. در مقاله عدد e دیدیم که کسب بهره باعث میشود بهره بیشتری کسب کنید. سینوس نیز همین گونه است. نیروی بازگرداننده مسافت ما را به صورت !x^3/3- تغییر میدهد که نیروی بازگرداننده دیگری تشکیل میدهد که باید آن را نیز در نظر بگیریم.
یک فنر را تصور کنید: کشیدن فنر و سپس رها کردنش موجب میشود که به نقطهای دورتر از نقطه اولیه حرکت کند و سپس دوباره کشیده شود. بنابراین باید همه نیروهای بازگرداننده را در نظر بگیریم:
- y = x حرکت اولیه ما است که یک نیروی بازگرداننده ایجاد میکند.
- !y = -x^3/3 که یک نیروی بازگرداننده تولید میکند.
- !y = x^5/5 که یک نیروی بازگرداننده دیگر تولید میکند.
- !y = -x^7/7 که نیروی بازگرداننده دیگری تولید میکند.
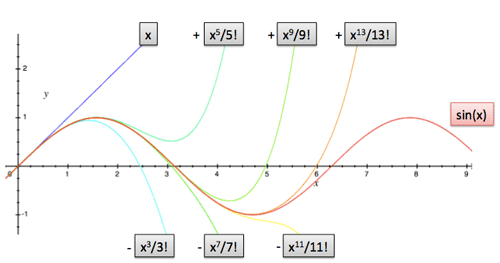
سینوس را نیز همانند e میتوان با استفاده از یک سری نامتناهی نمایش داد:

شاید این فرمول را بارها دیده باشید؛ اما زمانی معنی دقیق آن را متوجه میشوید که سینوس را به صورت ترکیبی از یک ضربه اولیه و نیروهای بازگرداننده در نظر بگیرید. کشش اولیه (y = x، در جهت مثبت) در نهایت بر نیروی بازگرداننده (در جهت منفی) غلبه میکند و سپس این نیرو بر نیروی بازگرداننده خود (که در جهت مثبت میکشد) غلبه میکند و همین طور تا آخر.
نکات مهم
- «نیروی بازگرداننده» را میتوان مانند «بهره مثبت یا منفی» در نظر گرفت. بدین ترتیب ارتباط سینوس /e در فرمول اویلر راحتتر درک میشود. سینوس نیز مانند e است به جز در مواردی که بهره منفی میگیرد.
- در زوایای خیلی کوچک «y=x» حدس خوبی برای سینوس محسوب میشود، چون فقط ضربه اولیه را داریم و نیروی بازگرداننده هنوز چندان قدرتی ندارد.
حسابان کسینوس
کسینوس در واقع همان سینوس جابجا شده است و اینک که سینوس را درک کردهایم، نباید در مورد آن نکته دشواری وجود داشته باشد.
- سینوس: از 0 آغاز میشود و در ضربه اولیه (y=x (100%
- کسینوس: از 1 آغاز میشود و هیچ ضربه اولیه وجود ندارد.
بدین ترتیب کسینوس از 1 آغاز میشود و نیروی بازگرداننده روی آن عمل میکند:
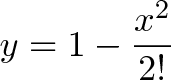
در این مورد نیز 1- را دو بار ادغام میکنیم تا به !x^2/2- برسیم؛ اما این بار نیروی بازگرداننده دیگری وارد عمل میشود:

تعریف 3: معادله دیفرانسیلی
ما رفتار سینوس را با استفاده از معادلات خاص تعریف کردیم. روش مختصرتر به صورت زیر است:
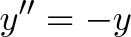
این معادله زیبا میگوید:
- موقعیت کنونی ما x است.
- شتاب ما (مشتق دوم y یا ''y) برابر با معکوس موقعیت کنونی (y-) است.
این واقعیت در مورد هر دو تابع سینوس و کسینوس صدق میکند. شاید در ابتدا از این تعریف چندان خوشتان نیاید چون تصور آن دشوار است؛ اما این فرمول ماهیت حقیقی سینوس را توصیف میکند و آن «میزان شتاب مخالف موقعیت کنونی» است.
آیا به خاطر دارید که سینوس و e چه ارتباطی دارند؟ e^x را میتوان به صورت معادله زیر توصیف کرد:
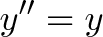
میبینیم که همان معادله سینوس است و تنها تفاوت در علامت مثبت است یعنی «شتاب برابر با موقعیت کنونی» است. با این که سینوس ارتفاع یک دایره است؛ اما ارتباط دادن آن با e واقعاً کار دشواری است.
یادگیری معادلههای دیفرانسیل یکی از مهمترین زمینههای ریاضیاتی محسوب میشود و البته داشتن دیدی شهودی از e نیز بسیار مهم است.
جمعبندی
هدف ما در این نوشته این بوده است که سینوس را از یک موضوع بیاهمیت ریاضیاتی (بخشی از دایره) جدا کرده و به صورت ماهیت واقعیاش بیان کنیم:
- سینوس حرکت هموار و منحنی بین کمینه 1- و بیشینه 1+ است. از نظر ریاضیاتی سینوس شتابی مخالف موقعیت کنونیاش دارد. این بهره منفی باعث میشود که سینوس تا ابد نوسان کند.
- سینوس در دایرهها و مثلثها (و فنرها، آونگها، نوسانها و بسیاری موارد دیگر...) ظاهر میشود.
- پی زمانی است که بین دو گذر سینوس از حالت خنثی به خنثی در (Sin(x طول میکشد. به طور مشابه پی به دایرهها تعلق ندارد و در موارد مختلفی استفاده میشود.
سینوس میتواند در موارد مختلفی به کمک شما بیابید. در نهایت باید مبانی ریاضیات یعنی عدد e، پی، رادیان، اعداد موهومی و موارد دیگر را به صورت شهودی بیاموزید تا بتوانید به صورتی مفید از آنها در محاسباتتان استفاده کنید.
اگر این مطلب برایتان مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای ریاضیات
- سینوس، کسینوس و تانژانت یک زاویه — به زبان ساده
- مجموعه آموزشهای دروس رسمی دبیرستان و پیش دانشگاهی
- قانون سینوس ها (Law of Sines) — به زبان ساده
- دایره مثلثاتی — به زبان ساده
- انتگرال توابع مثلثاتی — از صفر تا صد
==













بینظیر – نویسنده درک بالایی از ریاضیات داره
باسلام
از توضیحات تون خیلی خیلی ممنون و سپاسگذارم
خیلی پرمحتوا بود وکمی سنگین ودیگاه بسیار زیبایی ازریاضیات وسینوس بود سپاس
سلام ممنون از مطالب جالب و خواندنی و آموزندهای که در اختیار قرار داده اید