عدد پی چگونه کشف شد؟ — ریاضیات به زبان ساده

عدد پی (π) عدد رمزآمیزی است. مطمئناً می‌دانید که مقدار آن برابر با 3.14159 است، چون احتمالاً در یک کتاب چنین خوانده‌اید. اما اگر به چنین کتابی دسترسی نداشتید، و هیچ رایانه یا فرمول‌های حسابان وجود نداشت چطور؟ تصور کنید تنها به کمک ذهن خود و یک تکه کاغذ می‌خواهید عدد پی را محاسبه کنید.

ارشمیدس 2000 سال پیش عدد پی را بدون وجود ارقام اعشاری و یا حتی عدد صفر با دقت 99.9% محاسبه کرد. از این بالاتر او تکنیکی ابداع کرد که بنیاد حسابان را تشکیل می‌دهد. چه خوب است که روش کشف عدد پی در همه مدارس آموزش داده شود تا همه دانش آموزان با بنیان‌های حسابان بهتر آشنا شوند.

چگونه می‌توان عدد پی را محاسبه کرد؟

پی محیط دایره‌ای با قطر واحد است. این عدد را چگونه به دست می‌آوریم؟ فرض کنید عدد پی برابر با 3 باشد. دایره‌ای را با دقت بکشید و نخی را روی پیرامون آن قرار دهید و سپس طول نخ را با دقیق‌ترین خط کش اندازه‌گیری کنید.

فیلم آموزش حسابان ۱ – پایه یازدهم در فرادرس

کلیک کنید

ارشمیدس چگونه عدد پی را محاسبه کرد؟

ارشمیدس محیط دایره را نمی‌دانست؛ اما ناامید نشد و از آنچه می‌دانست یعنی محیط یک مربع آغاز کرد. البته او در واقع با یک شش‌ضلعی محاسبه خود را آغاز کرد؛ اما از آنجا که ترسیم و کار کردن با مربع آسان‌تر است، ما از مربع استفاده می‌کنیم.

ما محیط یک دایره را نمی‌دانیم؛ اما می‌توانیم آن را بین دو مربع رسم کنیم:

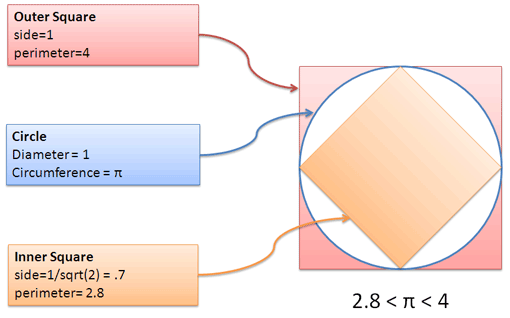
دقت کنید که این وضعیت شبیه مسیر مسابقه‌ای با یال‌های داخلی و خارجی است. محیط دایره هر چه که باشد بین محیط دو مربع قرار دارد، یعنی بیشتر از محیط مربع داخلی و کمتر از محیط مربع بیرونی است.

محیط مربع‌ها را می‌توانیم به سادگی محاسبه کنیم:

• مربع بیرونی (آسان): ضلع = 1 و از این رو محیط = 4 است.
• مربع بیرونی (نه چندان آسان): قطر = 1 و از این رو با استفاده از قضیه فیثاغورس مجموع مربعات اضلاع برابر 1 است. بنابراین ضلع = $$\sqrt{1 \over2}$$ یا 0.7 , از این رو محیط برابر با 3.4 = 0.7 × 4 است.

ما نمی‌دانیم که پی چقدر است؛ اما می‌دانیم که عددی بین 2.8 و 4 است. اگر تصور کنیم دقیقاً نیمه این دو کرانه باشد، پس باید در حدود 3.4 باشد.

مربع ‌دقت کمی دارد؛ اما شش‌ضلعی دقت‌ بیشتری ارائه می‌کند. بدین ترتیب ما توانستیم مقدار عدد پی را برابر با 3.4 تخمین بزنیم؛ اما اگر صادقانه بگوییم خط کش و نخ تقریب بهتری به دست می‌داد. چرا حدس ما این‌قدر کم‌دقت است؟

مربع‌ها گوشه‌دار هستند. آن‌ها را نمی‌توان چندان شبیه دایره دانست و این اختلاف موجب محاسبات نادرست و با اشتباه زیاد می‌شود؛ اما با افزایش اضلاع، برای مثال با استفاده از هشت‌ضلعی می‌توانیم حدس بهتری از عدد پی داشته باشیم:

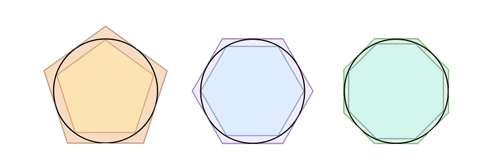
چنان که می‌بینید با افزایش تعداد اضلاع، به شکل یک دایره نزدیک‌تر می‌شویم.

بنابراین محیط یک هشت‌ضلعی چیست؟ آیا فرمول محاسبه آن را می‌دانید. شاید هم بهتر باشد که برای تقریب بهتر از 16 ضلعی یا حتی 32 ضلعی استفاده کنیم. آیا محیط این شکل‌ها را می‌دانید؟

البته سؤالات فوق پرسش‌های دشواری هستند. خوشبختانه ارشمیدس از روش‌های خلاقانه‌ای برای محاسبه محیط شکل‌ها هنگام دو برابر کردن اضلاع آن‌ها استفاده می‌کرد.

محیط درونی: یک قطعه از درون (مانند ضلع یک مربع) برابر با $$sin ({x\over2})$$ است که x زاویه داخلی یک ضلع است. برای نمونه یک ضلع مربع برابر با $$sin ({90 \over2}) = sin (45) = 0.7$$ است. محیط کامل در این صورت برابر با 2.8 = 0.7 × 4 خواهد بود که قبلاً محاسبه کردیم.

محیط بیرونی: یک قطعه از شکل بیرونی برابر با $$tan({x \over 2})$$ است که x زاویه یک ضلع است. بنابراین یک قطعه از محیط بیرونی برابر با tan(45) = 1 و محیط کامل برابر با 4 است.

دقت کنید که در این جا یک فرمول ساده داریم و افزودن اضلاع باعث کاهش زاویه‌ها می‌شود:

محیط مربع درونی به صورت $$sin ({90 \over2}) × 4$$ است.

هشت‌ضلعی 8 زاویه 135 درجه دارد که محیط درونی $$sin ({135\over2}) × 8$$ به دست می‌آید.

در واقع با استفاده از یک مربع (4 ضلع) دقتی برابر با 91% داریم و هنگام استفاده از هشت‌ضلعی (8 ضلع) دقت به 98% افزایش می‌یابد.

اما مشکلی وجود دارد، ارشمیدس ماشین حسابی که مجهز به دکمه Sin باشد نداشت! در عوض وی از گزاره‌های مثلثاتی برای بازنویسی سینوس و تانژانت برحسب مقادیر پیشین آن‌ها استفاده می‌کرد:

• محیط بیرونی جدید [میانگین هارمونیک]:

• محیط درونی جدید[میانگین هندسی]:

در این فرمول‌ها تنها از حساب استفاده شده و ربطی به مثلثات ندارند. از آنجا که از اعداد مشخصی مانند $$\sqrt{2}$$ و 1 آغاز کردیم می‌توانیم به طور مکرر از این فرمول استفاده کرده و تعداد ضلع‌ها را افزایش دهیم تا تقریب بهتری از عدد پی به دست آوریم.

بررسی فرمول

با شروع از چهار ضلع (مربع)، مسیر حرکت به سمت تقریب بهتر عدد پی را آغاز می‌کنیم:

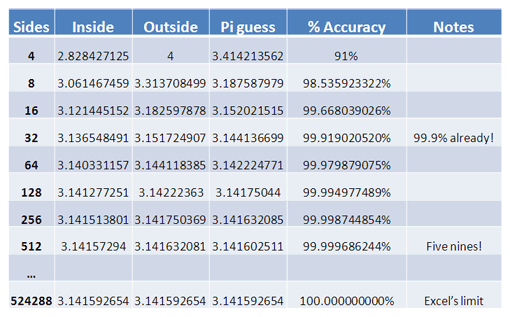
در هر دور تعداد اضلاع را دو برابر (4، 8، 16، 32، 64) و بازه‌ای که پی قرار دارد را محدودتر می‌کنیم. فرض کنید عدد پی در نیمه مسیر بین کران‌های بیرونی و درونی باشد.

پس از 3 گام (32 ضلع) ما به دقت 99.9% دست یافته‌ایم. پس از 7 گام (512 ضلع) ما عدد پی را تا 9 رقم مشهور داریم. و پس از 17 گام (با بیش از نیم میلیون ضلع) تقریب ما از عدد پی به بیشینه محدودیت دقت اکسل می‌رسد. در واقع باید از ارشمیدس به خاطر این فرمول خوب متشکر باشیم.

متأسفانه اعداد اعشاری در سال 250 قبل از میلاد هنوز اختراع نشده بودند، چه برسد به نرم‌افزارهای صفحه گسترده. بنابراین ارشمیدس مجبور بود که این فرمول‌ها را به کمک کسرها حل کند. او کار خود را با شش‌ضلعی آغاز کرد و با 12، 24، 48 و 96 ضلع ادامه داد. آیا تاکنون تلاش کرده‌اید ریشه دوم عددی را صرفاً با کسرها محاسبه کنید؟ تخمین نهایی وی از عدد پی با استفاده از شکلی با 96 ضلع به صورت زیر بود:

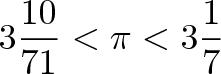
نقطه میانی این بازه برابر با 3.14185 است که تقریباً 99.9% دقیق است!

اگر به کسرها علاقه‌مند هستید، کسر متقارن عجیب $${355\over 113}$$ تخمین فوق‌العاده دقیقی (99.99999%) از عدد پی محسوب می‌شود و بهترین تخمینی است که بشر برای بیش از یک هزاره در دست داشته است.

برخی افراد از کسر $${22\over 7}$$ برای عدد پی استفاده می‌کنند؛ اما با توجه به این که $${22\over 7}$$ در محاسبات 2000 سال پیش ارشمیدس صرفاً کران بالا محسوب می‌شد، استفاده از آن در این زمان کمی عجیب است.

نقش حسابان در محاسبه عدد پی چیست؟

ارشمیدس با حسابان آشنایی نداشت و از طریق آغاز تهیه یک مدل خام (استفاده از مربع برای تقلید دایره) و بهبود آن، صرفاً زمینه‌ای برای توسعه حسابان مهیا کرده است.

فیلم مجموعه آموزش ریاضیات – مقدماتی تا پیشرفته در فرادرس

کلیک کنید

حسابان پیرامون موضوعات زیر شکل یافته است:

• ما پاسخ را نمی‌دانیم؛ اما در مورد آن حدس‌هایی داریم. ما حدس‌هایی برای عدد پی داریم که عددی بین 2.8 و 4 است. در حسابان مفاهیم زیادی مانند سری تیلور برای ساخت حدس‌هایی با درجات مختلفی از دقت وجود دارد.
• می‌توان حدس را بهبود بخشید. ارشمیدس کشف کرد که افزودن اضلاع شکل باعث بهبود تخمین می‌شود. این‌ها روش‌های عددی برای بهینه‌سازی مکرر فرمول هستند. برای نمونه رایانه‌ها می‌توانند از یک حدس خام برای محاسبه جذر یک عدد، کار خود را آغاز کرده و آن را به طور مکرر بهبود بخشند و این روش از یافتن پاسخ از بیرون سریع‌تر است.
• شما می‌توانید فرار کنید؛ اما نمی‌توانید پنهان شوید. ما نمی‌دانیم که عدد پی دقیقاً چه مقدار است؛ اما می‌توانیم آن را بین دو کران به دام بیندازیم. با محدودتر کردن کران‌های بیرونی، می‌دانیم که عدد پی بین این دو کران قرار دارد. این مسئله به نام قضیه فشردگی نام دارد.
• پی یک عدد آرمانی دست‌نیافتنی است. یافتن مقدار عدد پی فرایندی است که هیچ گاه پایان نمی‌یابد. وقتی نماد π را می‌بینیم در واقع معنی آن چنین است: «اگر به کمال علاقه دارید، می‌توانید شروع به محاسبه عدد پی تا هر مقدار که دوست دارید بکنید؛ اما هر کس تا جایی که نیاز دارد آن را محاسبه می‌کند و سپس فرایند محاسبه را متوقف می‌سازد.»

در واقع محاسبه عدد پی به نیازهای ما بستگی دارد. یک شکل با 96 ضلع برای هر چیزی که ارشمیدس نیاز داشته بسازد، کافی بوده است.

ایده «به قدر کافی دقیق» تا حدودی غریب است، چون انتظار می‌رود که ریاضیات دقیق باشد. ریاضیات مدلی برای توصیف جهان است. اما در صورتی که کیهان و ابزارهایمان فازی باشند، لازم نیست معادله‌های ما چندان دقیق باشند.

درس‌هایی برای زندگی

حتی ریاضیات نیز می‌تواند درس‌های پنهانی برای زندگی روزمره ما داشته باشد. برخی اوقات «بهترین» دشمنِ «خوب» است. کمال‌گرایی به معنی این که باید مقدار دقیق عدد پی را داشته باشیم؛ می‌تواند باعث شود که یافتن نتایج خوب و قابل استفاده عدد پی را از دست بدهیم. چه در حال تخمین عدد پی باشید و یا به نوشتن نرم‌افزاری مشغول باشید، در هر حال می‌توانید نسخه اولیه خامی را ایجاد کنید و سپس در طی زمان آن را بهبود دهید و لازم نیست نگران مدل کامل باشید. دقت زیادی در همان گام‌های نخست به دست می‌آید و احتمالاً برای کسب دقت بیشتر باید کار زیادتری صورت بگیرد، یعنی تلاش زیاد برای بازدهی کم. این همان اصل پارتو است.

کشف عدد پی از سوی ارشمیدس، مثالی زنده و قوی است که باید همواره به خاطر داشته باشیم. همان طور که هندسه، شهود ما در مورد خطوط و زاویه‌ها را بهبود می‌بخشد، حسابان نیز قواعدی در مورد معادلات تعریف می‌کند که به مرور بهتر می‌شوند. نمونه‌هایی مانند محاسبه عدد پی به عنوان یک نقطه شروع به شهود ما کمک می‌کنند و بدین ترتیب از یادگیری ایده‌های جدید در خلأ جلوگیری می‌شود.

در مطالب بعدی به بررسی مفهوم «به قدر کافی خوب» می‌پردازیم. دقت کنید که 96 ضلع برای ارشمیدس به قدر کافی خوب بوده است و نیم میلیون ضلع نیز برای نرم‌افزار اکسل «به قدر کافی خوب» است. همیشه محدودیت‌هایی وجود دارند.