مدل آمیخته گوسی در خوشه بندی – پیاده‌سازی در پایتون

از الگوریتم‌های معروف در خوشه‌بندی، می‌توان به روش‌هایی اشاره کرد که براساس «مدل آمیخته گوسی» (Gaussian Mixture Model) عمل می‌کنند. به طور خلاصه این روش را با GMM نیز نشان می‌دهند. همانطور که مشخص است، در این شیوه خوشه‌بندی، فرض بر این است که هر خوشه از داده‌هایی با توزیع نرمال (گوسی) تشکیل شده و در حالت کلی نیز داده‌ها نمونه‌ای از توزیع آمیخته نرمال هستند. هدف از خوشه‌بندی مدل آمیخته گوسی یا نرمال، برآورد پارامترهای توزیع هر یک از خوشه‌ها و تعیین برچسب برای مشاهدات است. به این ترتیب مشخص می‌شود که هر مشاهده به کدام خوشه تعلق دارد. چنین روشی را در یادگیری ماشین، خوشه‌بندی برمبنای مدل می‌نامند.

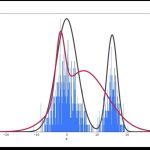
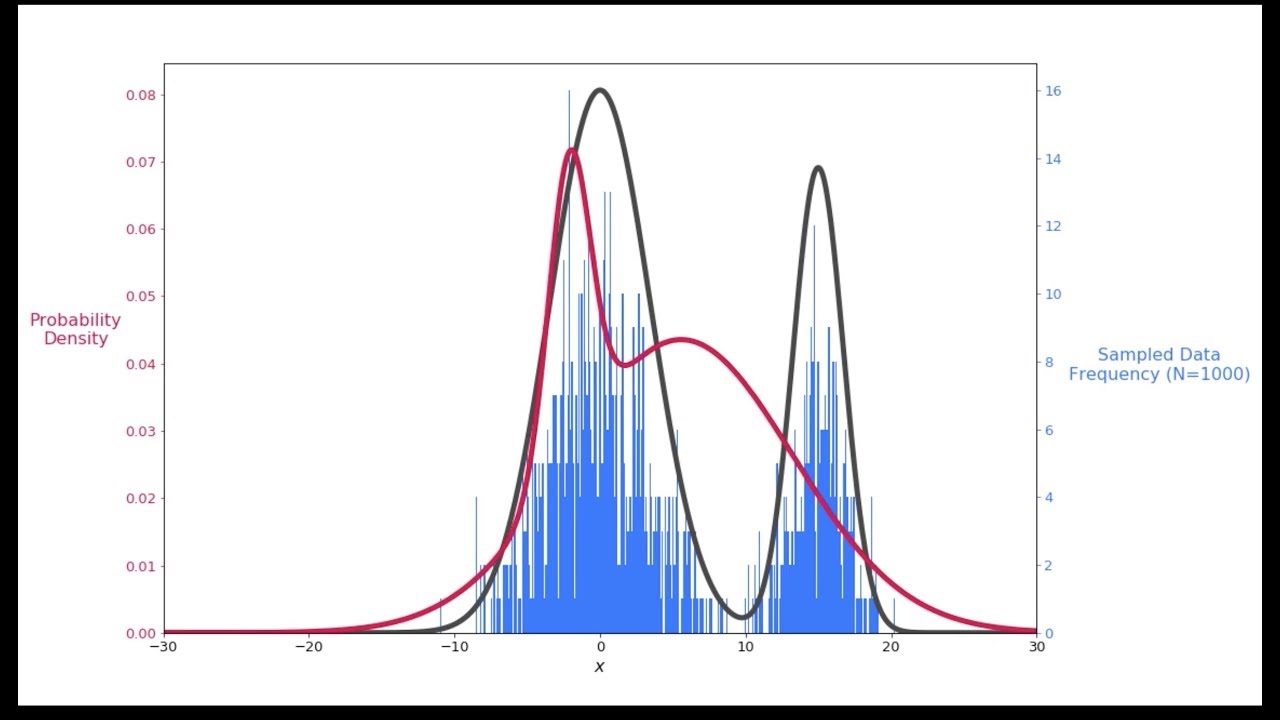
در شیوه خوشه‌بندی با مدل آمیخته گاوسی، برآورد پارامترهای توزیع آمیخته از یک «متغیر پنهان» (Latent Variable) استفاده می‌شود. به این ترتیب به کمک الگوریتم (EM (Expectation Maximization می‌توان برآورد مناسب برای پارامترها و مقدار متغیر پنهان به دست آورد.

برای آشنایی بیشتر با شیوه به کارگیری الگوریتم EM به مطلب الگوریتم EM و کاربردهای آن — به زبان ساده مراجعه کنید. همچنین برای آگاهی از اصول خوشه‌بندی نوشتار آشنایی با خوشه‌بندی (Clustering) و شیوه‌های مختلف آن را بخوانید. البته خواندن مطلب تابع درستنمایی (Likelihood Function) و کاربردهای آن — به زبان ساده و قضیه بیز در احتمال شرطی و کاربردهای آن نیز خالی از لطف نیست.

مدل آمیخته گوسی در خوشه‌ بندی

روش‌های خوشه‌بندی مانند kmeans قادر به شناسایی خوشه‌های کروی هستند و اگر ساختار خوشه‌ها خارج از این شکل باشد، عمل خوشه‌بندی توسط این الگوریتم‌ها به خوبی صورت نمی‌گیرد. به عنوان یک راه حل در چنین مواردی می‌توان از خوشه‌بندی برمبنای مدل یا همان مدل آمیخته گوسی استفاده کرد.

البته با توجه به ساختار خوشه‌های می‌توان از توزیع‌های دیگری نیز در این میان کمک گرفت ولی به طور معمول فرض می‌شود که مشاهدات مربوط به خوشه‌ها دارای توزیع نرمال هستند.

یک مدل آمیخته گاوسی را با نماد ریاضی به شکل زیر می‌نویسند. در اینجا منظور از $$\pi_k$$ وزن توزیع kام یا فراوانی مشاهدات از آن توزیع است.

$$\large p(x)=\sum_{k=1}^K\pi_k\cal{N}(x|\mu_k,\Sigma_k),\;\;\;\sum_{k=1}^K\pi_k=1$$

فرض کنید تعداد خوشه‌ها برابر با $$k$$ باشد. در اینجا پارامترهای توزیع گوسی (نرمال) نیز با $$\theta$$ نشان داده می‌شوند. متغیر پنهان که به صورت یک بردار، برچسب هر یک از مشاهدات را نشان می‌دهد با $$Z$$‌ مشخص شده‌ است. در این صورت مدل آمیخته گوسی یک بُعدی برای این خوشه‌های به صورت زیر نوشته می‌شود.

$$\large p(X|\theta)=\sum_z p(X,Z|\theta)$$

در نتیجه هدف از اجرای خوشه‌بندی برمبنای مدل، بیشینه‌سازی این تابع درستنمایی است.

نکته: توجه داشته باشید که مقدار z به صورت دو دویی یا باینری است به این معنی که اگر مشاهده nام به خوشه kام تعلق داشته باشد مقدار این متغیر برابر با ۱ و در غیر اینصورت برابر با صفر خواهد بود.

البته از آنجایی که بیشینه‌سازی این تابع با بیشینه‌سازی لگاریتم آن مشابه است و لگاریتم‌گیری، فرم تابع احتمال آمیخته گوسی (نرمال) را ساده‌تر می‌کند از رابطه زیر برای اجرای الگوریتم خوشه‌بندی برمبنای مدل استفاده خواهیم کرد.

$$\large \ln[(p(X|\theta)]=\ln \{\sum_z p(X,Z|\theta)\}$$

در تصویر زیر یک نمونه از توزیع آمیخته گاوسی (ترکیب سه متغیر تصادفی نرمال) را مشاهده می‌کنید.

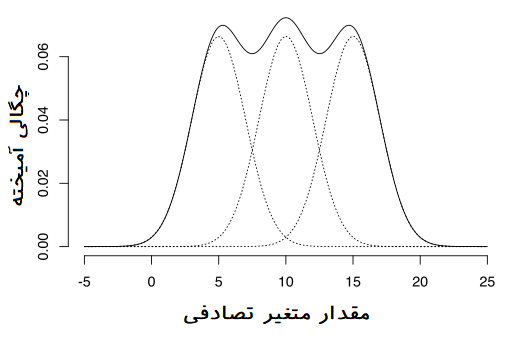
متاسفانه وجود پارامترهای زیاد در این تابع (مانند میانگین و واریانس و همچنین کوواریانس بین خوشه‌ها) امکان بیشینه‌سازی آن را با روش تحلیلی نمی‌دهد. بنابراین در چنین مواقعی استفاده از تکنیک‌های عددی مانند الگوریتم EM کارساز است.

الگوریتم EM

به منظور برآورد پارامترهای مدل آمیخته گاوسی از الگوریتم EM استفاده خواهیم کرد. این الگوریتم دارای دو بخش یا گام است. گام متوسط گیری یا Expectation و گام بیشینه‌سازی یا Maximization.

در گام اول (E-step) یا گام متوسط‌گیری، هدف برآورد توزیع متغیر پنهان به شرط وزن ($$\pi$$)، میانگین‌ها (Means) و ماتریس کوواریانس ($$\Sigma$$) توزیع آمیخته نرمال است. بردار پارامترها را در این جا با نماد $$\theta$$ نشان می‌دهیم. برای این کار ابتدا یک حدس اولیه برای این پارامترها زده می‌شود سپس گام‌های به ترتیب برداشته می‌شوند. همانطور که خواهید دید، حدس‌های اولیه را می‌توان بوسیله الگوریتم kmeans بدست آورد. به این معنی که برای خوشه‌های حاصل از الگوریتم kmeans، میانگین، ماتریس کوواریانس و وزن‌ها محاسبه می‌شود. توجه داشته باشید که منظور از وزن، درصدی (احتمال) از داده‌ها است که در یک خوشه قرار دارند.

در گام دوم (M-step) با استفاده از متغیرهای پنهان، سعی خواهیم کرد تابع درستنمایی را نسبت به پارامترهای $$\theta$$ بیشینه کنیم. این مراحل (گام E و گام M) تا زمانی که الگوریتم همگرا شود (مقدار تابع درستنمایی تغییر نکند)، ادامه خواهد داشت. به این ترتیب الگوریتم EM علاوه بر برآورد پارامترهای توزیع آمیخته گاوسی، برچسب‌ها یا مقدار متغیر پنهان را نیز مشخص می‌کند.

گام اول (E-Step) برای GMM

همانطور که قبلا اشاره شد، تابع توزیع آمیخته گاوسی را می‌توان به صورت ترکیب وزنی از چندین توزیع نرمال نوشت. بنابراین اگر وزن‌ها را با $$\pi_k$$ نشان دهیم، برای $$K$$ خوشه یا توزیع نرمال، تابع چگالی آمیخته در نقطه $$x$$ به صورت زیر نوشته خواهد شد.

$$\large p(x)=\sum_{k=1}^K \pi_k\cal{N}(x|\,u_l,\Sigma_k)$$

به کمک قانون بیز در احتمال شرطی تابع احتمال پسین برای متغیر پنهان $$Z$$ که به صورت $$\gamma(x_{nk})$$ نشان داده شده، به صورت زیر در خواهد آمد. البته در نظر داشته باشید که تابع احتمال پیشین در این حالت همان $$\pi$$ است.

$$\large \gamma(z_{nk})=\dfrac{\pi_k\cal{N}(x_n|\mu_k,\Sigma_k)}{\sum_{j=1}^K\pi_j\cal{N}(x_n|\mu_j,\Sigma_j)}$$

مشخص است که $$z_{nk}$$ مقدار متغیر پنهان برای مشاهده nام در خوشه kام است. همچنین باید توجه داشت که منظور از $$\mu_k$$، میانگین و $$\Sigma_k$$ نیز ماتریس کوواریانس خوشه kام در نظر گرفته شده است. برای سادگی به جای نوشتن تابع چگالی احتمال توزیع نرمال از نماد $$\cal{N}(x|\mu,\Sigma)$$ استفاده کرده‌ایم.

گام دوم (M-Step) برای GMM

پس از محاسبه تابع احتمال پسین برای متغیر پنهان، باید پارامترهای توزیع آمیخته گاوسی را برآورد کرده سپس مقدار لگاریتم تابع درستنمایی را محاسبه کنیم. این گام‌ها تا رسیدن به همگرایی در مقدار تابع درستنمایی تکرار خواهد شد.

میانگین برای خوشه‌ kام به صورت زیر برآورد می‌شود.

$$\large \mu_k^{new}=\dfrac{1}{N_K}\sum_{n=1}^N\gamma(z_{nk})x_n$$

ذکر این نکته نیز ضروری است که در رابطه بالا، $$N_k$$ تعداد اعضای خوشه kام را نشان می‌دهد. همچنین برای برآورد ماتریس کوواریانس خوشه kام نیز از رابطه زیر کمک می‌گیریم.

$$\large \Sigma_k^{new}=\dfrac{1}{N_K}\sum_{n=1}^N\gamma(z_{nk})(x_n-\mu_k^{new})(x_n-\mu_k^{new})^T$$

برای برآورد وزن‌ برای هر یک از توزیع‌ها نیز از رابطه زیر استفاده می‌کنیم.

$$\large \pi_k^{new}=\dfrac{N_k}{N}, \;\;\;N_k=\sum_{n=1}^N\gamma(xz_{nk})$$

به این ترتیب تابع که در ادامه قابل مشاهده است باید بیشینه شود.

$$\large \ln p(X|\mu,\Sigma,\pi)=\sum_{n=1}^N\ln \Big\{\sum_{k=1}^K\pi_k\cal{N}(x_n|\mu_k,\Sigma_k)\Big\}$$

حال با توجه به اینکه لگاریتم یک تابع مقعر محسوب می‌شود از نامساوی جنسن (Jensen Inequlity) استفاده کرده و سعی می‌کنیم تابع زیر که کران پایین برای تابع بالا است را بیشینه کنیم.

$$\large L=\sum_{n=1}^N\sum_{k=1}^K \operatorname{E}[z_{nk}]\Big\{\ln \pi_k+\ln {N}(x_n|\mu_k,\Sigma_k)\Big\}$$

این کارها و مراحل مبنای الگوریتم EM محسوب می‌شوند. در ادامه به کمک زبان برنامه‌نویسی پایتون و توابع آن الگوریتم EM را برای خوشه‌بندی برمبنای مدل GMM به کار خواهیم گرفت.

الگوریتم EM و پیاده سازی در پایتون

بعد از اینکه در مورد تئوری الگوریتم خوشه‌بندی برمبنای مدل آمیخته گاوسی صحبت کردیم، زمان پیاده‌سازی آن با پایتون رسیده است. به این منظور نقاط یا حدس اولیه را براساس روش خوشه‌بندی kmeans محاسبه و از این مقدارها برای الگوریتم EM استفاده خواهیم کرد.

فیلم آموزش خوشه بندی تفکیکی با نرم افزار آر R در فرادرس

کلیک کنید

کد زیر به این منظور تهیه شده است. البته توجه داشته باشید که منبع داده یک فایل متنی است که مربوط به مشخصات ای‌میل‌ها کاربران است. ابتدا کتابخانه‌ها را به همراه فایل داده فراخوانی می‌کنیم.

مشخص است که برای از بین بردن واحد اندازه‌گیری داده‌ها از تکنیک PCA‌ استفاده شده است. با توجه به خوشه‌سازی اولیه توسط الگوریتم kmeans بهتر است آن‌ها را به تصویر بکشیم. توجه دارید که خوشه‌بندی به روش kmeans ساختار کروی (Spherical) ایجاد کرده و تقریبا تعداد اعضای خوشه‌های یکسان خواهد بود. به همین دلیل این تکنیک برای داده‌های ما که ساختاری کروی ندارند، مناسب نخواهد بود. ولی به عنوان نقطه آغاز از نتایج آن استفاده خواهیم کرد. کد زیر به منظور ترسیم خوشه‌های به شیوه kmeans برای مشاهدات ایجاد شده است.

نتیجه اجرای این کد، نموداری به صورت زیر است.

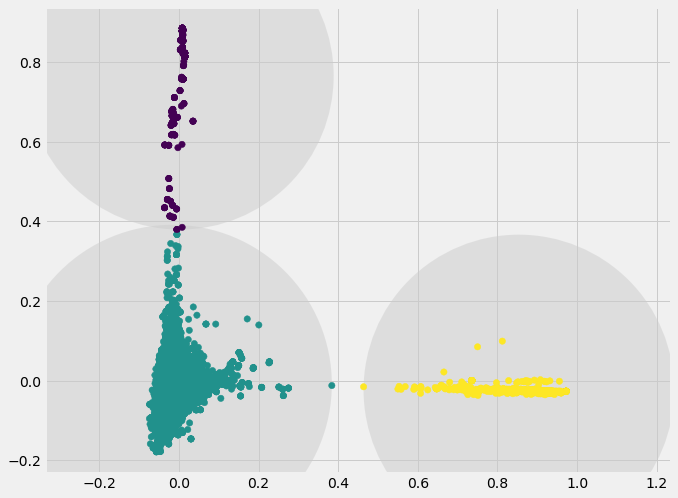
در تصویر زیر نتیجه خوشه‌بندی براساس GMM را روی یک مجموعه داده فرضی می‌بینید. به وضوح مشخص است که سه خوشه وجود دارد که البته ساختار کروی نیز دارند.

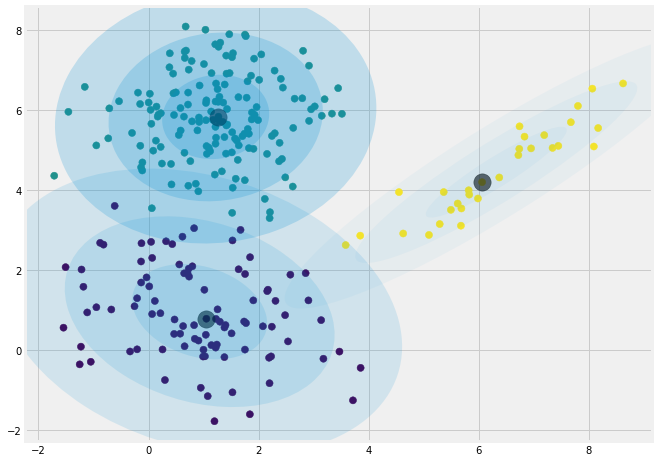
کلاس GMM در پایتون

برای تعریف خوشه‌بندی برمبنای مدل GMM کدهای زیر را تهیه کرده‌ایم.

فیلم آموزش کاهش تعداد رنگ تصاویر با استفاده از روش های خوشه بندی هوشمند در فرادرس

کلیک کنید

این کد براساس تعداد تکراری که در max_iter مشخص شده، محاسبات مربوط به الگوریتم EM را تکرار می‌کند.

قطعه کد بعدی به منظور استفاده از نقاط اولیه که توسط الگوریتم kmeans ایجاد شد، نوشته شده است. توجه داشته باشید که این قسمت فقط یک تابع است که در داخل برنامه اصلی صدا زده می‌شود. در داخلی این تابع شیوه محاسبه ماتریس کوواریانس که در قسمت قبل محاسبه شده است بازخوانی شده و به کار گرفته می‌شود.

حال لازم است که بخش E-step را در پایتون پیاده‌سازی کنیم. از آنجایی که در این گام به توزیع چندمتغیره نرمال احتیاج داریم بهتر است که با دستور زیر کتابخانه مربوطه را فراخوانی کنیم.

در کد زیر بخش مربوط به E-step برای الگوریتم خوشه‌بندی برمبنای مدل GMM نوشته شده است.

پس از آنکه تابع احتمال پسین برای Z بدست آمد، گام بیشینه‌سازی یا M-step آغاز می‌شود و برآورد برای پرامترهای توزیع آمیخته بدست می‌آید.

همانطور که دیده شد، ابتدا با استفاده از kmeans نقاط اولیه تولید و سپس با گام‌های E-step و M-step الگوریتم EM فعال شدند. با توجه به تعداد تکرار مجاز برای الگوریتم، مقدارهای پارامترها از جمله متغیر پنهان که برچسب مربوط به مشاهدات و تعلق به خوشه را مشخص می‌کند، برآورد شدند.

کدی که در ادامه قابل مشاهده است به منظور استفاده از مدل حاصل برای خوشه‌بندی داده‌هایی است که باید برچسب آن‌ها پبیش‌بینی شود. به همین دلیل تابع predict را تعریف کرده‌ایم. به این ترتیب احتمال تعلق هر مشاهده به خوشه‌ها توسط predict_proba محاسبه می‌شود. با این کار می‌توان هر مشاهده را به خوشه‌ای متعلق دانست که بزرگترین احتمال را برای آن دارد.

در ادامه برنامه‌ای نوشته شده است که براساس سه توزیع مختلف نرمال، داده‌ها را خوشه‌بندی می‌کند. از نتایج حاصل از این برنامه برای ترسیم خوشه‌ها استفاده خواهیم کرد.

تصویری که توسط این برنامه ایجاد می‌شود، خوشه‌ها را به خوبی نشان می‌دهد. مشخص است که ظاهر این خوشه‌ها کروی نبوده و حتی ممکن است بعضی از داده‌ها مربوط به دو خوشه به یکدیگر نزدیکتر (از نظر فاصله اقلیدسی) نیز باشند ولی از آنجایی که در توزیع احتمال آن خوشه قرار ندارند، با هم در یک خوشه قرار نگرفته‌اند.

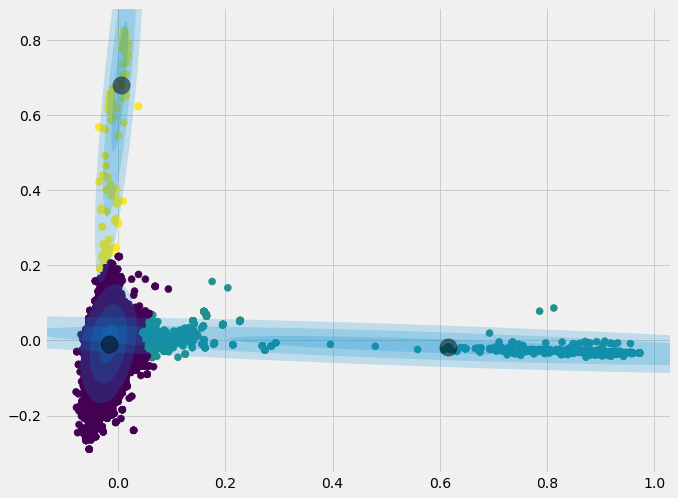
همانطور که مشخص است برعکس تصویر قبلی توزیع‌ها به یکدیگر وابسته بوده و دارای کوواریانس غیر صفر (یا همبستگی مخالف صفر) هستند.

استفاده از کتابخانه sklearn برای GMM

کتابخانه sklearn نیز ابزارات متنوع و خوبی برای خوشه‌بندی برمبنای مدل برای توزیع آمیخته گاوسی (GMM) دارد.

به منظور بررسی ابزارات این کتابخانه، مسئله قبلی را با توجه به توابع موجود در این کتابخانه مجددا مورد بررسی قرار می‌دهیم.

به نظر می‌رسد نتایج شبیه هستند. البته اگر در مقدار مربوط به مراکز هر خوشه تفاوتی به نظر برسد، علت می‌تواند استفاده از نقاط اولیه متفاوت در کتابخانه sklearn و کدهایی باشد که در بخش بالایی ظاهر شده بود. به هر حال حاصل خوشه‌بندی مشاهدات به یکدیگر بسیار شبیه است.

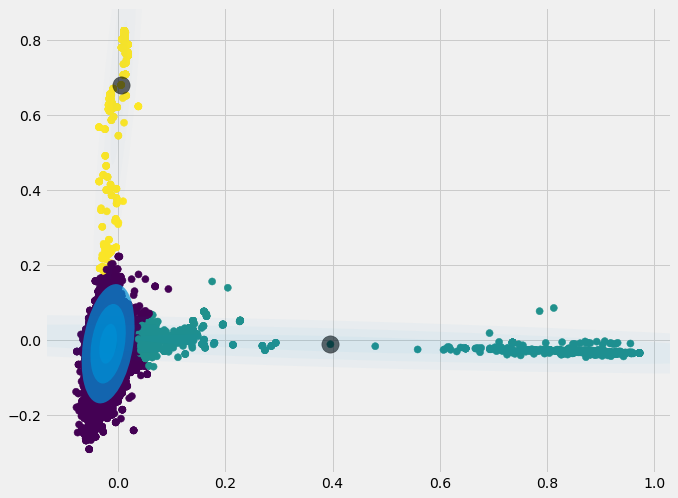
به منظور دسترسی به کدها و حفظ توالی آن‌ها، در ادامه برنامه کامل GMM در پایتون در قالب یک class نوشته شده است.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های یادگیری ماشین و بازشناسی الگو
• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• مجموعه آموزش های داده کاوی یا Data Mining در متلب
• آموزش خوشه بندی K میانگین (K-Means) با نرم افزار SPSS
• آموزش خوشه بندی سلسله مراتبی با SPSS
• آشنایی با خوشه‌بندی (Clustering) و شیوه‌های مختلف آن

^^